La méthode de régression linéaire est une méthode d’entraînement machine supervisé utilisée par l’outil Entraîner à l’aide d’AutoML et qui recherche une équation linéaire décrivant le mieux la corrélation des variables explicatives avec la variable dépendante. Cela s’effectue en ajustant une ligne aux données utilisant le moins de carrés. La ligne tente de minimiser la somme des carrés des valeurs résiduelles. La valeur résiduelle est la distance séparant la ligne de la valeur réelle de la variable explicative. Rechercher la ligne la mieux ajustée est un processus itératif.
Voici l’exemple d’une équation de régression linéaire résultante :
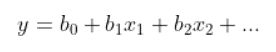
Dans l’exemple ci-dessus, y est la variable dépendante et x1, x2, etc., sont les variables explicatives. Les coefficients (b1, b2, etc.) expliquent la corrélation des variables explicatives avec la variable dépendante. Le signe des coefficients (+/-) indique si la variable est corrélée positivement ou négativement. b0 est l’intersection qui indique la valeur de la variable dépendante en supposant que toutes les variables explicatives sont égales à 0.
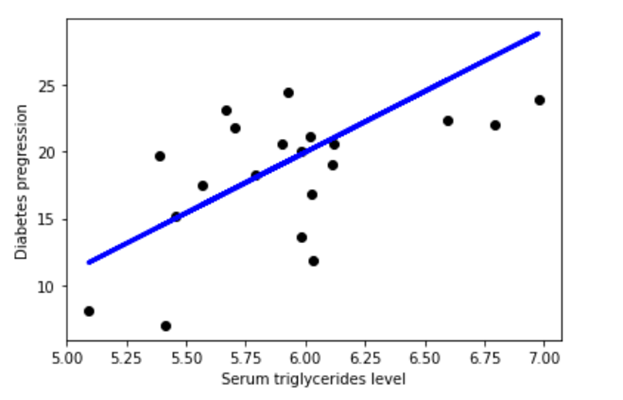
Dans l’image suivante, un modèle de régression linéaire est décrit par la ligne de régression y = 153,21 + 900,39x. Le modèle décrit la relation existant entre la variable dépendante, la progression des diabètes et la variable explicative, le niveau de triglycérides sériques. Une corrélation positive est présentée. Cet exemple montre un modèle de régression linéaire comportant deux variables. Bien qu’il ne soit pas possible de visualiser les modèles comportant plus de trois variables, dans la pratique, un modèle peut posséder un nombre quelconque de variables.
Un modèle de régression linéaire aide à prédire la valeur d’une variable dépendante et à expliquer le degré de précision de la prévision. Cela est reflété par les valeurs R-carré et valeur p. La valeur R-carré indique quel degré de la variation dans la variable dépendante peut être expliqué par la variable explicative et la valeur p explique le degré de fiabilité de cette explication. Les valeurs R-carré vont de 0 à 1. Une valeur égale à 0,8 signifie que la variable explicative peut expliquer 80 pour cent de la variation dans les valeurs observées de la variable dépendante. Une valeur égale à 1 indique qu’une prévision parfaite peut être effectuée, ce qui rare en pratique. Une valeur égale à 0 signifie que la variable explicative n’aide pas du tout à prévoir la variable dépendante. Avec une valeur p, vous pouvez vérifier si l’effet de la variable explicative sur la variable dépendante diffère significativement de 0.
Ressources supplémentaires
Vous avez un commentaire à formuler concernant cette rubrique ?