Cómo funciona Estimar el tiempo hasta el evento

La herramienta Estimar el tiempo hasta el evento predice el tiempo hasta que ocurra un evento durante una serie de observaciones en función del tiempo de observaciones anteriores del evento y los atributos concretos de las observaciones. La entrada debería ser una mezcla de registros que han experimentado el evento y los registros que no han experimentado el evento. La herramienta incorpora variables explicativas y estima si acortan o alargan el tiempo hasta el evento. La herramienta también predice el tiempo adicional hasta que se produzca el evento durante las observaciones que todavía no han experimentado el evento.

This video was created with ArcGIS Pro 3.5.

Cada observación de la tabla o las entidades de entrada deben tener campos que contienen la antigüedad de la observación, un indicador de si el evento ya ha ocurrido, y las variables explicativas. Estos campos se proporcionan en el campo Antigüedad, el campo Indicador de evento y los parámetros Variables explicativas, respectivamente. Las variables explicativas pueden ser continuas o categóricas, y el indicador de evento solo debe tener los valores 0 (el evento no ha ocurrido) o 1 (el evento ha ocurrido). En el caso del campo de antigüedad, a menudo incluirá la antigüedad actual del individuo, pero, en general, es la cantidad de tiempo a partir del primer posible tiempo en que podría haber ocurrido el evento y el final del momento en que ha ocurrido (o el tiempo actual, si el evento no ha ocurrido). Por ejemplo, para estimar la duración de los árboles, los valores del campo de antigüedad deben ser la antigüedad actual del árbol, si está vivo, o la antigüedad del árbol cuando murió. Sin embargo, para estimar el tiempo hasta el nuevo arresto, los valores del campo deben ser la cantidad de tiempo desde que el individuo fue excarcelado (la primera vez que podría ocurrir un nuevo arresto) hasta el momento del nuevo arresto (o la fecha actual si el individuo no se ha arrestado de nuevo). No es necesario proporcionar la unidad de la antigüedad (horas, días, años, etc.), pero todos los resultados deben interpretarse en esa unidad de tiempo.

La herramienta produce una variedad de salidas, numéricas y gráficas, para entender cómo afectan las variables explicativas al tiempo hasta el evento, predecir cuándo ocurrirá el evento y evaluar la precisión y fiabilidad del modelo.

Potenciales aplicaciones

Los modelos de tiempo hasta el evento son útiles en una serie de campos en los que el objetivo es estimar cuánto tarda en ocurrir un evento y qué factores influyen en su cronología. A continuación se ofrecen algunas de las posibles aplicaciones de la herramienta:

• Mantenimiento de infraestructura: estime el tiempo hasta que la tubería gotee, un puente necesite reparaciones importantes o un transformador falle. Las variables explicativas podrían incluir el tipo de material (categórico), la exposición a clima extremo (categórico) y la carga de tráfico (continuo).
• Gestión forestal: modelo de tiempo hasta que un árbol tiene un diámetro determinado, necesita cosecharse o sucumbe a la enfermedad. Las variables explicativas podrían incluir el diámetro inicial del tronco (continuo), la especie (categórico), la calidad del suelo (continuo) y la competencia de árboles cercanos (categórico).
• Crédito predeterminado: prediga el tiempo hasta el impago de un préstamo por parte de un prestatario. Las variables explicativas podrían incluir el importe del préstamo (continuo), la puntuación de crédito (continuo), el tipo de empleo (categórico) y el historial de crédito (categórico).
• Retención de clientes: estime cuándo cancelará su suscripción un cliente o cambiará de proveedores de servicios. Las variables explicativas podrían incluir el importe de la factura mensual (continuo), la duración del contrato (categórico), el número de reclamaciones de servicio del cliente (continuo) y los descuentos promocionales que ha recibido (categórico).
• Fabricación: vaticine cuándo una máquina requerirá mantenimiento o tendrá que reemplazarse. Las variables explicativas podrían incluir las horas de funcionamiento (continuo), el modelo de máquina (categórico) y la temperatura de la planta (continuo).

Análisis de tiempo hasta el evento y análisis de supervivencia

El análisis de tiempo hasta el evento es una rama de la estadística que calcula, explica y pronostica cuándo ocurrirá un evento durante una serie de observaciones, en la que se supone que cada observación percibirá el evento después de algún tiempo. El análisis de tiempo hasta el evento se utiliza de forma generalizada en la investigación médica, en la que suele llamarse análisis de supervivencia porque el evento que se modela es la muerte de un individuo. Por este motivo, gran parte de la terminología y los conceptos del análisis de tiempo hasta el evento se toman prestados del análisis de supervivencia. Por ejemplo, la cantidad de tiempo hasta que la observación advierte el evento se denomina duración y la curva de estimación del tiempo hasta el evento se denomina curva de supervivencia. En el caso de aplicaciones como la predicción de la muerte de un árbol o de cuándo fallará una infraestructura, la terminología se adapta de forma natural, pero es menos clara; esto es evidente, por ejemplo, cuando se estima el tiempo hasta un nuevo arresto. En ese caso, el tiempo de supervivencia de un individuo será la cantidad de tiempo que transcurre hasta que se vuelva a arrestar a un individuo. De forma similar, cuando se habla de la probabilidad de que no se vuelva a arrestar a individuo en cinco años, se formula como la probabilidad de que el tiempo de supervivencia supere los cinco años. Este tema cambiará entre el tiempo hasta los eventos y los tiempos de supervivencia dependiendo del contexto, pero se referirá a lo mismo.

Otra diferencia entre el análisis del tiempo hasta el evento y el análisis de supervivencia consiste en que el análisis de supervivencia se centra principalmente en calcular el efecto de un tratamiento (por lo general, un fármaco en periodo de ensayo clínico) en el tiempo de supervivencia y se centra menos en predecir los tiempos de supervivencia de personas individuales. Básicamente, la pregunta es si el fármaco aumenta los tiempos de supervivencia, en lugar de cuánto vivirá un individuo concreto. Sin embargo, el análisis del tiempo hasta el evento se centra más en predecir cuándo ocurrirá un evento durante observaciones individuales y está menos centrado en estimar si las variables explicativas aumentarán o reducirán el tiempo de supervivencia. Aunque todos los modelos de análisis de supervivencia pueden utilizarse en análisis del tiempo hasta el evento (y viceversa), algunos modelos son más adecuados para unos que para otros. En concreto, esta herramienta utiliza un modelo de tiempo de fallo acelerado paramétrico que es más adecuado para predecir el tiempo hasta el evento, mientras que en los ensayos clínicos suele usarse un modelo de riesgos proporcionales de Cox no paramétrico, que resulta más apropiado para calcular el efecto de los tratamientos médicos.

Curvas de supervivencia

Al estimar el tiempo hasta el evento, se crea una curva de supervivencia para cada observación, dependiendo de sus variables explicativas. La curva de supervivencia es una función que traza gráficamente la probabilidad de que el tiempo de supervivencia supere una cantidad de tiempo determinada (es decir, la probabilidad de que el individuo siga vivo después de un cierto tiempo). La curva de supervivencia siempre empieza en 1 y se reduce a lo largo del tiempo hasta 0. Por ejemplo, la curva de supervivencia siguiente se parece a de los seres humanos.

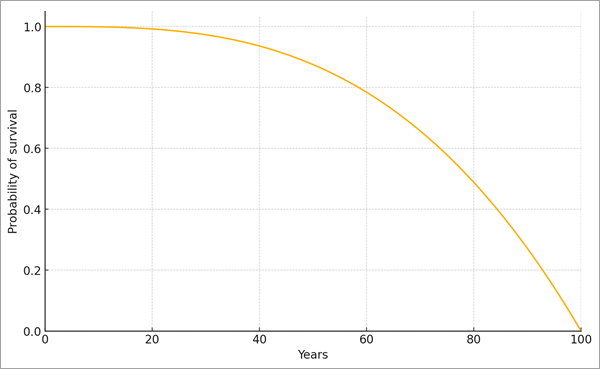
En esta curva, la gran mayoría de los individuos vive más de 20 años antes de que la proporción empiece a acelerar la decadencia. A los 60 años, algo menos del 80 por ciento de las personas sigue viva. El tiempo medio de supervivencia (0,5 en el eje y) es de aproximadamente 80 años y casi ninguna persona llega a los 100 años.

A partir de la curva de supervivencia se puede cualquier cuantil de tiempo hasta el evento. Por ejemplo, el percentil ⁵ del tiempo hasta el evento es el valor del eje x cuando la curva equivale a 0,95 (cuando existe un 95 por ciento de probabilidad de que el evento no haya ocurrido todavía) y el percentil ⁷⁵ es cuando la curva equivale a 0,25. Estos cuantiles pueden utilizarse para crear intervalos de confianza; por ejemplo, el tiempo entre los percentiles ⁵ y ⁹⁵ es un intervalo de confianza del 90 por ciento para el tiempo hasta el evento. Aunque puede calcularse cualquier cuantil, las curvas de supervivencia suelen resumirse mediante la mediana del tiempo de supervivencia (el valor del eje x cuando la curva de supervivencia es igual a 0,5).

Modelo de tiempo de fallo acelerado

El modelo estadístico utilizado para estimar los tiempos hasta el evento se denomina modelo de tiempo de fallo acelerado (AFT). En el funcionamiento de los modelos AFT se supone que cada observación envejece a un ritmo diferente, dependiendo de sus variables explicativas individuales. Por ejemplo, a menudo se dice (aunque no es verdad) que los perros envejecen siete veces más rápido que los seres humanos, que la edad de 3 años en un perro equivale a 21 años en los seres humanos. En otro ejemplo puede considerar que dos puentes pueden deteriorarse a una velocidad diferente. Un puente podría tener 30 años de antigüedad y considerarse igual de deteriorado que otro que solo tiene 10 años, dependiendo de los atributos de los puentes, como el material de construcción, el volumen de tráfico y las condiciones ambientales.

En los modelos AFT, el efecto de las variables explicativas es acelerar o desacelerar el tiempo hasta el evento y esto se expresa como factor de tiempo. El factor de tiempo entre dos observaciones, A y B (cada una con variables explicativas diferentes), es la relación de las duraciones previstas de A y B. Por ejemplo, un factor de tiempo de 1,3 indica que se espera que la duración de la observación A sea un 30 por ciento más larga que la observación B. De forma similar, un factor de tiempo de 0.6 significa que se espera que sea un 40 por ciento más corta. Si el factor de tiempo es 1, se espera que ambas observaciones tengan la misma duración. Hay que tener en cuenta que el factor de tiempo comprende una línea de base o referencia con la que se compara (en este caso, la duración de la observación B).

El efecto del factor de tiempo consiste en alargar la curva de supervivencia horizontalmente. Por ejemplo, en la imagen siguiente se muestran cuatro curvas de supervivencia que reflejan el efecto de los factores de tiempo de 1 (curva azul con la que se compara), 2 (curva naranja), 3 (curva verde) y 4 (curva roja), de izquierda a derecha. Es difícil ver que las curvas son versiones alargadas las unas de las otras, por lo que se dibuja una línea de puntos horizontal en el tiempo medio de supervivencia. Obsérvese que el tiempo medio de supervivencia correspondiente al factor de tiempo 2 es el doble que el tiempo medio correspondiente al factor de tiempo 1. De forma similar, el tiempo medio de supervivencia de los factores de tiempo 3 y 4 son tres y cuatro veces el tiempo medio de supervivencia correspondiente al factor de tiempo 1, respectivamente. Aunque la línea de puntos se sitúa en la media, el uso de cualquier otro valor del eje x también mantendrá estos coeficientes.

El uso de la curva azul del extremo izquierdo como línea de base ha sido una elección arbitraria. Si, en lugar de esto, se define la curva roja del extremo derecho como línea de base para la comparación, los factores de tiempo serían 0,25, 0,5, 0,75 y 1 (de izquierda a derecha). Estos factores de tiempo inferiores a 1 indican que la curva de supervivencia roja tiene la supervivencia prevista más larga entre las cuatro curvas.

La herramienta estimará un factor de tiempo para cada variable explicativa, probará la relevancia estadística del factor de tiempo y mostrará el resultado en el mensaje (consulte la sección Mensajes de geoprocesamiento siguiente para obtener más información). La interpretación del factor de tiempo depende de si la variable explicativa es categórica o continua, puesto que define las líneas de base de manera diferente. En el caso de las variables categóricas, debe designarse una categoría como categoría de referencia, y se crearán factores de tiempo para todas las demás categorías comparadas con la categoría de referencia. Por ejemplo, si un campo de variable categórica tiene valores únicos A, B y C y la categoría A es la categoría de referencia, los factores de tiempo solo se calcularán para las categorías B y C. Si el factor de tiempo para la categoría B es 2,2, significa que se estima que una observación de categoría B dure 2,2 veces más que una observación de categoría A, suponiendo que todos los demás atributos sean igual (o, lo que es lo mismo, que las curvas de supervivencia de la categoría B se alargan 2,2 veces más que las curvas de supervivencia de la categoría A). La herramienta utiliza la primera categoría ordenada alfanuméricamente como categoría de referencia, pero el usuario puede reclasificar los valores de campo para cambiar la categoría que se utilizará como categoría de referencia.

En el caso de las variables continuas, el factor de tiempo es el cambio de la duración correspondiente a un incremento de una unidad en la variable explicativa. En este caso, se comparan dos observaciones que difieren exactamente en 1 con respecto al valor de la variable explicativa (el resto de variables explicativas son iguales). Por ejemplo, cuando se calculan tres duraciones, si el diámetro del tronco en metros es una variable explicativa, el factor de tiempo mide el aumento (o la reducción) de la duración aumentando el diámetro del árbol en 1 metro. Si los árboles con diámetro de tronco más grande tienden a vivir más tiempo, el factor de tiempo será superior a 1 y si tienden a vivir menos, el factor de tiempo será menor que 1. Como el factor de tiempo es un multiplicador, un aumento de dos unidades en la variable explicativa multiplicará la duración por el factor de tiempo al cuadrado, el aumento de tres unidades de la variable explicativa multiplicará la duración por el factor de tiempo al cubo y así sucesivamente. La naturaleza compuesta del factor de tiempo correspondiente a las variables explicativas continuas puede causar problemas de modelado (consulte la sección Prácticas recomendadas, limitaciones y flujo de trabajo sugerido a continuación para obtener información y recomendaciones).

Estimación del modelo AFT

El modelo AFT utiliza una distribución de Weibull para modelar la curva de supervivencia:

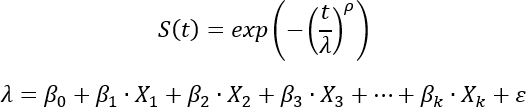
El parámetro de escala (λ) se calcula como modelo lineal de variables explicativas (X_i) y coeficientes estimados (β_i). El parámetro de escala controla la cantidad de extensión de la curva de supervivencia, como se describe en la sección anterior. Los atributos particulares de una observación alargarán (o contraerán) la curva de supervivencia de esa observación de forma intuitiva, dependiendo de si sus atributos se asocian generalmente con duraciones mayores o menores.

Todas las observaciones comparten el parámetro de forma (ρ), que permite que la curva de supervivencia adopte varias formas en el mismo intervalo de tiempo. En la imagen siguiente se muestran formas diferentes de las distribuciones de Weibull con el mismo parámetro de escala:

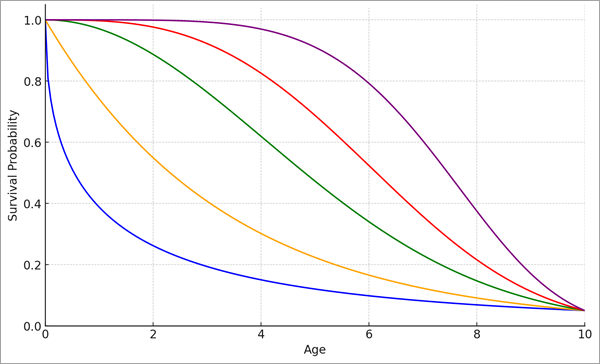
El parámetro de forma a veces se denomina parámetro de aceleración porque está relacionado con si la curva de supervivencia se acelera o se desacelera. La aceleración se mide mediante la función de riesgo, que se define como la probabilidad de que ocurra el evento en un momento determinado, suponiendo que el evento no haya ocurrido antes de ese momento. Por ejemplo, si es más probable que los puentes más antiguos necesiten repararse en un futuro próximo que los puentes más recientes, la función de riesgo aumenta con el tiempo (en otras palabras, los puentes más antiguos tienen mayor riesgo que los más recientes), por lo que la curva de supervivencia se acelera con el tiempo. Por el contrario, si es menos probable que los puentes más antiguos tengan que repararse en un futuro próximo que los puentes más recientes, el índice de riesgo se reduce y la curva de supervivencia se desacelera. Los valores del parámetro de forma superiores a 1 indican una curva de supervivencia en aumento y los valores menores que 1 indican una supervivencia en desaceleración. Sin embargo, el modelo no puede calcular los diversos índices de riesgo, en los que la curva de supervivencia se acelera y desacelera en momentos diferentes (por ejemplo, la duración humana presenta un riesgo más alto en bebés, luego disminuye en niños y adultos jóvenes y aumenta de nuevo en las personas mayores).

Todos los coeficientes y el parámetro de forma se calculan utilizando la probabilidad máxima y la herramienta los muestra como mensajes.

Observaciones censuradas y predicción

En las secciones anteriores se muestra cómo se calculan las curvas de supervivencia de cada observación, ya haya ocurrido o no el evento de la observación. Por ejemplo, se puede crear una curva de supervivencia para un puente que ya se ha deteriorado. En esencia, esta curva de supervivencia muestra la duración prevista del puente si se construye con los mismos atributos hoy. Aunque esta información puede ser útil, resulta mucho más útil para crear curvas de supervivencia que pronostiquen la duración adicional de las observaciones en las que el evento no ha ocurrido (por ejemplo, predecir cuánto tiempo más durará un puente existente hasta que necesite repararse).

Las observaciones en las que el evento aún no ha ocurrido se denominan observaciones censuradas y las observaciones en las que el evento ha ocurrido se denominan observaciones sin censura. Esta terminología proviene del hecho de que las observaciones sin censura tienen información completa (se conoce el tiempo de supervivencia), pero las observaciones censuradas solo tienen información parcial; no se conoce el tiempo de supervivencia exacto, pero se sabe que es más largo que una cierta cantidad de tiempo (la edad actual de la observación). Esto es comparable a la idea de que un documento puede estar sin censurar o censurado: toda la información del documento puede estar disponible (un documento sin censurar) o partes pueden estar redactadas por un censor (un documento censurado).

En el caso de las observaciones censuradas, el objetivo es crear una curva de supervivencia que estime el tiempo adicional hasta el evento, según su antigüedad actual. Esta curva de tiempo de supervivencia adicional puede crearse supeditándola a la cantidad de tiempo que el individuo ha vivido ya. Desde el punto de vista matemático, la curva de tiempo de supervivencia adicional, S_Add(T), se calcula como S_Add(T) = S(C+T)/S(C), donde T son unidades de tiempo adicional tras el tiempo de censura C.

La curva de tiempo de supervivencia adicional puede visualizarse como un reajuste a escala de la curva de supervivencia de la observación después del tiempo de censura. Por ejemplo, en la imagen siguiente se muestra una curva de supervivencia de una observación que se censuró en el tiempo 4. Basándose en las variables explicativas, había aproximadamente un 60 por ciento de probabilidad de que el individuo viviera al menos cuatro unidades de tiempo (el valor del eje y en el tiempo de censura). Sin embargo, como se sabe que el individuo ha vivido al menos cuatro unidades de tiempo (tiempo de censura), los valores del eje y se reajustan a escala para empezar de nuevo en 1 (en otras palabras, hay una probabilidad del 100 por cien de que el individuo viva al menos cuatro unidades de tiempo). De forma similar, el eje x comienza en 0 otra vez para medir el tiempo futuro a partir del tiempo de censura. En este ejemplo, el tiempo medio de supervivencia de un individuo con estas variables explicativas es aproximadamente cinco unidades de tiempo (donde la curva cruza 0,5 en el eje y original), pero si se sabe que el individuo ya ha vivido cuatro unidades de tiempo, el tiempo medio de supervivencia adicional es de dos unidades de tiempo, más o menos, (donde la curva cruza 0,5 en el eje y ajustado a escala más pequeño) durante un intervalo total de seis unidades de tiempo. En otras palabras, saber que el individuo ya ha vivido cuatro unidades de tiempo aumenta la duración media total de aproximadamente cinco unidades de tiempo a seis unidades de tiempo más o menos. Cuanto más dura la observación antes de ser censurada, más tiempo se espera que sobreviva en comparación con su curva de supervivencia de línea de base.

En las observaciones censuradas, las curvas de supervivencia que muestran los tiempos adicionales hasta el evento tras la censura aparecen en los gráficos emergentes de la tabla o las entidades de salida. En los gráficos emergentes también se muestran las curvas de supervivencia individuales de las entidades censuradas y sin censurar.

La antigüedad de la observación en el tiempo de censura normalmente será la antigüedad actual de la observación, pero también puede ser la antigüedad con respecto al momento en que el individuo se observó por última vez, como la fecha de inspección más reciente de un puente. En ese caso, el tiempo de supervivencia adicional comienza en la antigüedad de la última observación.

Curva de Kaplan-Meier

Como cada combinación de variables explicativas resulta en una curva de supervivencia diferente, puede ser difícil cuantificar si se prevé que una observación particular tenga una duración más larga o más corta que una observación típica. Algunas de las variables explicativas de la observación aumentan la duración y otras la reducen, pero no está claro si, en total, alargan o acortan la duración de la observación. Para proporcionar una curva que puede utilizarse como base de la comparación con curvas de supervivencia individuales, la herramienta calcula una curva de Kaplan-Meier para los datos.

La curva de Kaplan-Meier es una estimación no paramétrica de la función de supervivencia que ignora las variables explicativas y calcula la proporción de observaciones que no han experimentado el evento a lo largo del tiempo. Esto se hace mediante el ajuste secuencial para el evento y los tiempos de censura utilizando la siguiente ecuación:

En la ecuación, E_i es el número de eventos que ocurrieron en el momento t_i, y N_i es el número de observaciones que no experimentaron el evento o se han censurado antes del tiempo t_i.

La curva se visualiza como una función escalonada que reduce cada tiempo en que ocurre el evento. La curva no puede extenderse después del tiempo del valor de campo de antigüedad más largo y la probabilidad de supervivencia nunca descenderá por debajo del porcentaje de individuos que se censuraron. Por ejemplo, en la curva de Kaplan-Meier siguiente, el valor más alto del campo de antigüedad era aproximadamente 3500 (el valor máximo del eje x) y algo más del 40 por ciento de las observaciones se censuraron (el valor más bajo de la curva es algo mayor que 0,4).

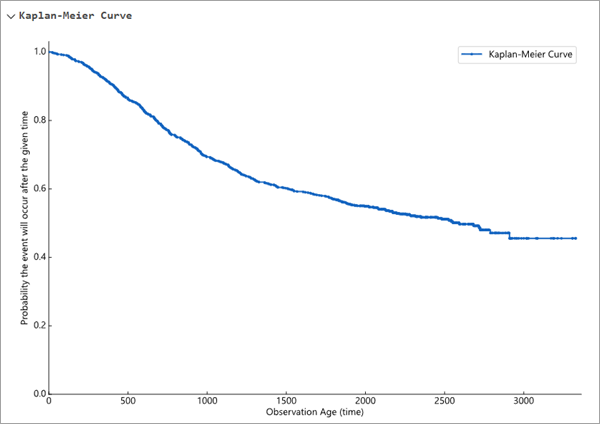
La curva de Kaplan-Meier correspondiente a los datos se muestra en una sección contraíble de los mensajes de geoprocesamiento. También se muestra en los gráficos emergentes de las entidades de salida o en la tabla para que pueda compararse directamente con las curvas de supervivencia de las observaciones individuales (para más información, consulte la siguiente sección).

Salidas de la herramienta

La herramienta devuelve una diversidad de salidas para investigar los resultados. Las salidas incluyen una tabla o clase de entidad de salida, mensajes de geoprocesamiento, gráficos emergentes y un histograma.

Entidades o tabla de salida

Para la entidad de entrada, se dibujará la capa de entidades de salida basada en el tiempo medio adicional hasta el evento. Las entidades censuradas se dibujan en tonos de rojo y rosa con tonos más intensos que indican que está previsto que el evento ocurra antes. Las entidades sin censurar se dibujan en gris claro y se configuran para dibujar debajo de las entidades censuradas si sus símbolos se superponen.

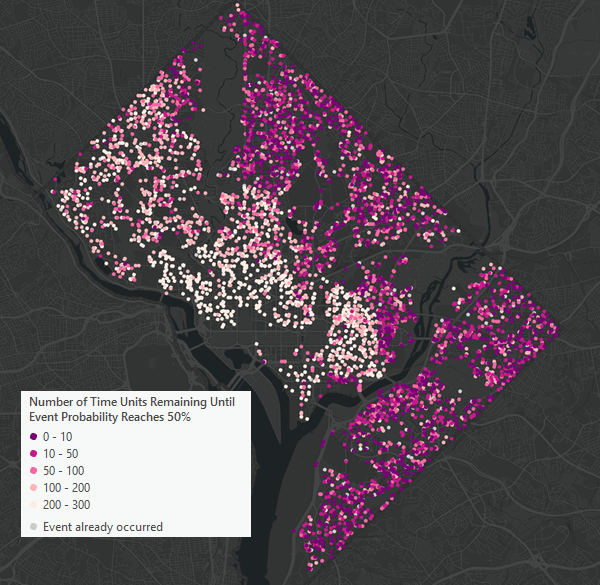
La salida de las entradas de entidad y tabla contendrá copias de todos los campos de entrada, junto con varios cuantiles de tiempo adicional hasta el evento. Los campos contendrán los percentiles ⁵, ¹⁰, ²⁵, medio (⁵⁰), ⁷⁵, ⁹⁰ y ⁹⁵ del tiempo adicional hasta el evento. Puede utilizar estos valores para crear rangos para el momento en que es probable que ocurra el evento, por ejemplo, mediante el uso de los percentiles ⁵ y ⁹⁵ para crear un intervalo de confianza del 90 por ciento. En el caso de las entidades no censuradas, todos los valores del campo cuantil contendrán valores nulos porque predecir cuándo ocurrirá el evento no es necesario si el evento ya ha ocurrido.

Gráficos emergentes

Si se activa el parámetro Habilitar elementos emergentes de curva de supervivencia, las entidades de salida o la tabla también contendrán un campo de gráficos emergentes para cada observación. En el caso de las entidades, puede acceder a los gráficos emergentes haciendo clic en la entidad del mapa mediante el uso de la herramienta Explorar. Cuando se trata de las tablas, es posible acceder a los gráficos emergentes haciendo clic con el botón derecho en la fila del registro de la tabla de atributos.

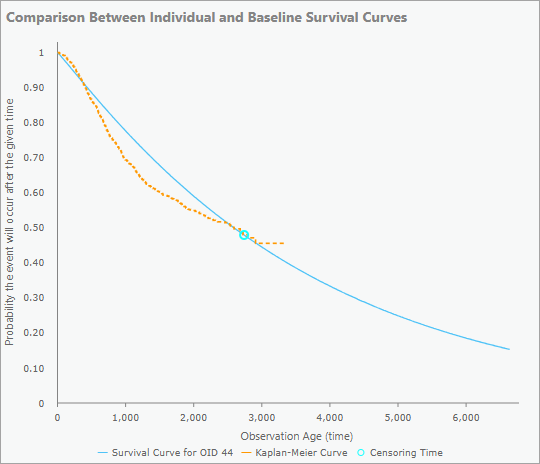
En el caso de las observaciones sin censurar, el gráfico emergente mostrará la curva de supervivencia de la entidad (curva azul) y un punto azul que indica el tiempo del evento. Esto permite ver si la observación percibió el evento antes o después en su duración prevista. Las observaciones con eventos muy anteriores o posteriores a lo previsto por el modelo podrían requerir más investigación. La curva de Kaplan-Meier (curva naranja) también se incluye en el gráfico emergente como base de la comparación. Esto permite ver si se esperaba que la observación sobreviviese más o menos que una observación típica. Por ejemplo, en la imagen siguiente, la curva de supervivencia es mejor y está a la izquierda de la curva de Kaplan-Meier, lo que significa que se esperaba que el evento ocurriese antes que para la mayoría de las observaciones. El punto azul también está en el centro de la curva de supervivencia, lo que significa que el evento ha ocurrido aproximadamente cuando el modelo predijo que lo haría, en función de sus variables explicativas.

Nota:

El eje x de los gráficos emergentes se extenderá hasta que la curva de supervivencia llegue a 0,1 (se necesita un valor de corte porque las curvas de supervivencia nunca llegan a cero). Sin embargo, como la curva de Kaplan-Meier no se puede extender más de lo establecido en el valor del campo de antigüedad, a menudo finalizará antes de que la curva de supervivencia llegue a 0,1. Para garantizar que la curva Kaplan-Meier se pueda ver, el eje x nunca se extenderá más del doble de la longitud de la curva de Kaplan-Meier, aunque la curva de supervivencia todavía no haya llegado a 0,1.

En el caso de las entidades censuradas, los gráficos emergentes también contendrán la curva de supervivencia y la curva de Kaplan-Meier de la observación, pero el tiempo de censura se indicará mediante un círculo azul en lugar de un punto.

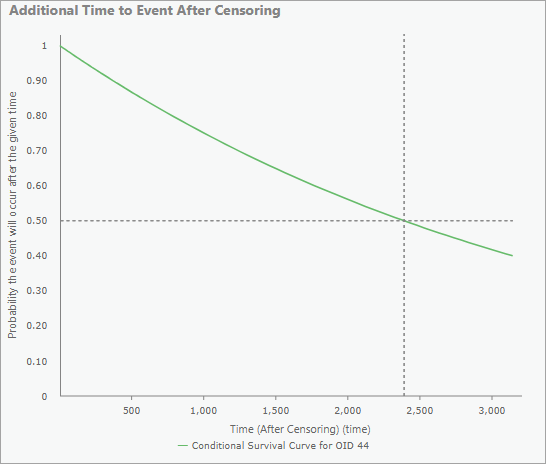
En el caso exclusivo de las entidades censuradas, los gráficos emergentes también contendrán un gráfico del tiempo adicional hasta el evento después de la censura. El tiempo medio adicional se dibuja como líneas de puntos horizontales y verticales para identificar el tiempo cuando el modelo predice que el evento habrá ocurrido con un 50 por ciento de probabilidad. El eje x se extenderá hasta que la curva llegue a 0,4 para garantizar que siempre se muestre la mediana.

Puede pasar el cursor por cualquiera de los gráficos emergentes para ver los valores particulares de las curvas.

Mensajes de geoprocesamiento

Los mensajes de geoprocesamiento contienen varias secciones en las que se resumen los efectos de las variables explicativas y los diagnósticos relacionados con lo bien que el modelo se ajusta a los datos.

Variables explicativas continuas

La primera sección de los mensajes contiene una tabla en la que se resumen los efectos de las variables explicativas continuas. Por cada variable, la tabla muestra el factor de tiempo, el coeficiente y su error estándar (a partir del parámetro de la escala de distribución de Weibull), la puntuación z y el valor p que prueba la relevancia estadística del coeficiente, así como los límites superior e inferior de un intervalo de confianza del 95 por ciento del factor de tiempo.

Al final se incluye una fila para el término de intercepción, pero los valores sin procesar normalmente carecen de una interpretación significativa. En cambio, la finalidad de la intercepción es escalar las curvas de supervivencia según la unidad de tiempo del campo de antigüedad. Por ejemplo, si ha convertido los valores de campo de antigüedad de horas a días, todos los factores de tiempo deberían seguir igual, pero el factor de tiempo de la intercepción se dividiría entre 24 (conversión de horas a días). Esto explica por qué no es necesario especificar la unidad del campo de antigüedad en la herramienta y arrojará resultados equivalentes con independencia de la unidad.

Nota:

El modelo AFT calcula directamente el coeficiente y el error estándar de cada variable, y demuestra su relevancia estadística mediante una prueba de z. Entonces se calcula el factor de tiempo a partir del coeficiente tomando su exponencial: exp(coefficent). Suele preferirse los factores de tiempo a los coeficientes porque los primeros se interpretan en relación con el tiempo de supervivencia bruto, mientras que los coeficientes se interpretan con relación al logaritmo del tiempo de supervivencia. Los límites de confianza superior e inferior se calculan creando un intervalo de confianza para el coeficiente y calculando el exponencial de los extremos.

Variables explicativas categóricas

La segunda sección de los mensajes contiene una tabla en la que se resumen los efectos de las variables explicativas categóricas. Por cada variable categórica se muestra una tabla en la que se indica el efecto de cada una de sus categorías. La categoría de referencia se muestra sobre la tabla y todos los factores de tiempo deben interpretarse en relación con su categoría. Por ejemplo, en la imagen siguiente, la variable categórica es el número de distrito y el distrito 1 es la categoría de referencia. Las observaciones del distrito 2 duran 5,345 veces más que las observaciones del distrito 1 (factor de tiempo equivalente a 5,345), pero las observaciones del distrito 8 son un 23,6 por ciento más breves que las del distrito 1 (factor de tiempo equivalente a 0,764). Los valores p también indican que los distritos 4, 5 y 7 no son significativamente diferentes del distrito 1.

Nota:

Cada variable categórica se convierte en una serie de variables binarias (0 o 1) y estas variables binarias se utilizan como variables explicativas continuas en el modelo AFT. Se crean variables binarias (K-1) para las categorías K y cada categoría recibe una variable binaria, excepto la categoría de referencia (este proceso se denomina codificación de indicador). Debe excluirse una categoría y utilizarse como referencia porque la inclusión de las variables binarias para todas las categorías da lugar a una colinealidad perfecta, que hace que el modelo no pueda calcular los coeficientes y los factores de tiempo.

Parámetro de forma de Wibull

Después de las tablas de coeficientes de variables explicativas, los mensajes muestran una tabla en la que se resume el parámetro de forma de la distribución de Weibull. La tabla también contiene la puntuación z y el valor p que demuestra si el parámetro de forma es estadísticamente diferente de 1. Además, se proporcionan los límites superior e inferior del intervalo de confianza del 95 por ciento.

El parámetro de forma determina si la curva de supervivencia se acelera o se desacelera. Los valores mucho más altos que 1 indican aceleración, lo que significa que, cuanto más antigua es la observación, mayor es la probabilidad de experimentar el evento en un futuro próximo. Los valores mucho más bajos que 1 indican desaceleración, lo que significa que, cuanto más reciente es la observación, mayor es la probabilidad de experimentar el evento en un futuro próximo. Los valores que no son significativamente distintos de 1 indican que las observaciones recientes y antiguas tienen la misma probabilidad de experimentar el evento en el futuro próximo. En el modelo se supone que la curva de supervivencia se acelera o desacelera de manera constante, pero no se puede cambiar entre ellos.

Estadísticas de resumen del modelo

La sección final del mensaje es la sección de resumen del modelo, que contiene la estadística relacionada con la precisión general de las predicciones y el ajuste del modelo. La sección muestra las estadísticas siguientes:

• Índice de concordancias: valor entre 0 y 1 que indica la probabilidad de que el modelo pueda predecir correctamente si un individuo tendrá una vida más larga que otro. Los valores próximos a 1 indican que el modelo puede predecir prácticamente siempre qué individuo experimentará el evento primero y los valores próximos a 0,5 indican que el modelo no es mejor que la casualidad a la hora de predecir el orden de los eventos. Los valores inferiores a 0,5 rara vez se observan, lo que indicaría que el modelo es menos preciso que la casualidad al hacer la predicción. El valor se calcula como proporción de pares de individuos en los que el modelo predice correctamente cuál de los dos experimenta el evento primero. Las entidades censuradas no se utilizan en el cálculo porque no se conocen sus tiempos de supervivencia. En la práctica, el valor típico se encuentra entre 0,6 y 0,8.
• AIC: criterio de información de Akaike (AIC) correspondiente al ajuste del modelo AFT. Este valor es informativo principalmente, pero puede utilizarse en flujos de trabajo avanzados, por ejemplo, para construir pruebas de razón de verosimilitud anidadas entre diferentes combinaciones de variables explicativas.
• Valor p: valor p de una prueba de repercusión general de las variables explicativas. El valor indica si las variables explicativas juntas mejoran significativamente las predicciones del modelo. Si este valor no es estadísticamente significativo (suele ser un valor mayor que 0,05), el modelo no funciona significativamente mejor que no proporcionar ninguna variable explicativa. El valor se determina utilizando una prueba de razón de verosimilitud.

Histograma de residual de desviación

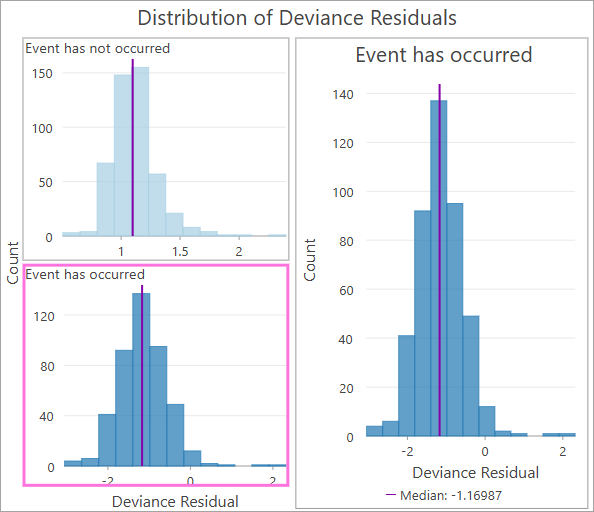
La capa de entidades de salida también incluye un histograma de los residuales de desviación de las observaciones. Desde el punto de vista conceptual, los residuales de desviación son similares a los residuales de otros modelos de regresión porque cuantifican si una observación ha tenido una duración más corta o más larga de lo que ha pronosticado el modelo. Los residuales de desviación positivos significan que el individuo ha vivido más de lo previsto, mientras que los residuales de desviación negativa indican que el individuo ha vivido menos (hay que tener en cuenta que algunas fuentes definen los signos, positivo o negativo, al contrario). Si el modelo se ajusta bien, el promedio de los residuales de desviación debería ser un valor próximo a cero.

En el caso de las observaciones sin censurar, algunas tendrán una duración mayor o menor de lo que el modelo predice, por lo que los residuales de desviación pueden ser positivos y negativos. Sin embargo, los residuales de desviación de las observaciones censuradas siempre serán positivos. Por esta razón, el histograma se divide en función del campo indicador del evento, que muestra histogramas separados para observaciones censuradas y sin censurar.

Los residuales de desviación resultan más útiles para investigar los valores atípicos de los resultados y los valores extremos de ambos histogramas indican cosas diferentes. En el caso de las observaciones sin censurar, los valores negativos extremos indican que la observación ha percibido el evento mucho antes de lo que se pronostica en el modelo y los valores positivos extremos indican que el evento se ha percibido mucho después. Los valores mayores que tres en cualquier dirección probablemente indican valores atípicos u observaciones anómalas que podrían requerir más investigación o la eliminación del dataset. En el caso de las observaciones censuradas, los valores son menos significativos, pero generalmente miden en qué momento se encontraba la observación cuando se censuró. Los valores del extremo izquierdo (próximos a cero) indican que la observación se censuró muy pronto en su duración, mientras que los valores del extremo derecho indican que se censuró muy tarde (posiblemente ya haya durado más de lo que predice el modelo, incluso antes de censurarse).

Los residuales de desviación se calculan con la siguiente ecuación:

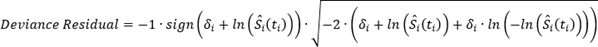
En la ecuación, S-hat_i(t_i) es la probabilidad de supervivencia estimada de la observación en el momento del evento (o en el momento en que se censura) y δ_i es el indicador del evento.

Nota:

Los residuales de desviación de las observaciones censuradas siempre son positivos porque, si un individuo ya ha sobrevivido cualquier cantidad de tiempo, se vaticina que tendrá una duración total más larga de lo que predice la curva de supervivencia de línea de base (consulte la imagen de la sección Observaciones censuradas y predicción anterior para conocer el motivo). Este proceso garantiza que la media general de los residuales de desviación (censurados y sin censurar) es cero para los modelos especificados correctamente.

Prácticas recomendadas, limitaciones y flujo de trabajo sugerido

La herramienta plantea una serie de limitaciones y desafíos. A continuación se ofrecen recomendaciones generales y las mejores prácticas a la hora de utilizar la herramienta:

• Predecir cuándo ocurrirá un evento en el futuro plantea dificultades, por lo que recomendado mantener expectativas realistas. La herramienta solo puede extraer información de las variables explicativas que proporciona el usuario, pero los fenómenos complejos, como la rotura de la infraestructura, implican numerosos factores que a menudo suelen muy particulares y específicos de cada individuo. En la práctica, normalmente debería considerar los tiempos previstos hasta el evento como indicaciones generales del momento en que podría ocurrir el evento, en lugar de predicciones muy concretas de fechas particulares. También debería ser particularmente precavido y escéptico al extrapolarlo a tiempos más remotos que el tiempo del evento más largo de los datos de entrada. Aunque a menudo son imprecisos, los resultados del análisis del tiempo hasta el evento pueden seguir siendo muy útiles para proporcionar estimaciones generales de costes futuros o priorización y asignación de recursos a observaciones que más probablemente perciban el evento después.

• Los modelos de tiempo hasta el evento no son intrínsecamente espaciales, pero la incorporación de información espacial podría mejorar el modelo al tomar en cuenta los patrones geográficos. Considere la posibilidad de agregar variables explicativas espaciales, como regiones geográficas como variables explicativas categóricas o distancias a entidades clave como variables explicativas continuas. Por ejemplo, al modelar la mortalidad de los árboles urbanos, la distancia hasta el edificio más cercano podría ser importante debido a la reducción de la luz solar provocada por las sombras del edificio.

• En el modelo se asume que el evento ocurrirá durante cada observación después de una cierta cantidad de tiempo, pero esto no es así en algunos casos. Por ejemplo, al predecir el tiempo hasta el nuevo arresto, algunos individuos nunca serán arrestados otra vez, pero el modelo seguirá vaticinando una curva de supervivencia para ellos. En la práctica, si el tiempo para la supervivencia adicional pronosticado durante una observación es muy largo, puede indicar la probabilidad de que el evento no ocurra nunca.
• En el caso de las variables explicativas continuas, los factores de tiempo son el cambio multiplicativo en la curva de supervivencia correspondiente a un incremento de una unidad en la variable explicativa. Sin embargo, el cambio de una unidad es mínimo para algunas variables y resulta en factores de tiempo muy próximos a 1 incluso para variables explicativas muy significativas e importantes. Por ejemplo, al predecir cuándo necesitará repararse los tejados, el tamaño del edificio en metros cuadrados podría utilizarse como variable explicativa. Sin embargo, aunque el tamaño del edificio sea muy importante, el aumento en un metro cuadrado solamente tendría un efecto insignificante en la curva de supervivencia. Si una de las variables explicativas es muy significativa (puntuación z alta y valor p bajo), pero tiene un factor de tiempo impreso de 1,000 o muy próximo a este valor, considere la posibilidad de dividir los valores del campo por un valor constante alto. Por ejemplo, dividir la variable de metros cuadrados por 100 producirá curvas de supervivencia idénticas y resultados significativos, pero el factor de tiempo ahora se interpretará como el cambio correspondiente a un aumento de 100 metros cuadrados en el tamaño del edificio, lo que podría generar un factor de tiempo más interpretable. Multiplicar o dividir cualquiera de las variables explicativas (o el campo de antigüedad) por un valor constante originará curvas de supervivencia equivalentes, por lo que se incentiva el reajuste a escala de los valores si facilita la interpretación de los resultados.
• Como el factor de tiempo es multiplicativo, los valores grandes (en comparación con los valores del resto de los datos) de cualquier variable explicativa continua puede causar inestabilidad y curvas de supervivencia cortas o largas sin motivo. El factor de tiempo representa el cambio correspondiente al aumento de la variable explicativa en una unidad y esto crece exponencialmente. Por ejemplo, un aumento de la variable explicativa en cinco unidades alarga la curva de supervivencia de acuerdo con el factor de tiempo a la quinta potencia. Estos exponentes pueden llegar a ser muy grandes y producir curvas de supervivencia inestables cuando se trata de la variable explicativa con valores altos. Los valores atípicos serán especialmente problemáticos, pero incluso los valores altos que no son valores atípicos pueden producir curvas de supervivencia inestables. En estos casos, una posible solución es aplicar una transformación logarítmica a la variable explicativa. Esto hará que el factor de tiempo de la variable explicativa sea más difícil de interpretar (ahora es la extensión de la curva de supervivencia correspondiente al aumento de una unidad en el logaritmo de la variable explicativa), pero convertir la variable explicativa a una escala logarítmica a menudo contrarresta el efecto combinado del factor de tiempo y produce curvas de supervivencia más razonables.

• Mientras que la estimación de los parámetros del modelo utilizan observaciones censuradas y sin censurar, las observaciones sin censurar facilitan el máximo de información porque se conoce su tiempo de supervivencia exacto. En general, se recomienda tener al menos 10 observaciones sin censurar por variable explicativa. Sin embargo, las variables categóricas deberían contarse como variables múltiples. Una variable categoría con dos categorías se considera una variable, con tres categorías cuenta como dos variables, con cuatro categorías como tres variables y así sucesivamente. Asimismo, cada categoría debería tener varias observaciones sin censurar para estimar mejor el efecto de todas las categorías de la variable categórica.

• En algunos casos puede resultar difícil definir el punto inicial de la duración de una observación. Por ejemplo, los puentes se someten a reparación y mantenimiento periódicos, por lo que, al predecir el tiempo hasta las siguientes reparaciones necesarios, la fecha inicial podría ser la fecha de construcción del puente o la fecha en la que hubo que reparar el puente por última vez. En este caso, tendrá que decidir si un puente reparado se considera equivalente a un puente nuevo. Si decide que los puentes reparados son equivalente a los nuevos, se podría incluir un solo puente en los datos varias veces para facilitar la creación del modelo (uno para cada vez que hubo que hacer reparaciones). Sin embargo, si decide que un puente reparado no es equivalente a un puente nuevo, podría intentar utilizar el número de veces anteriores que hubo que reparar el puente como variable explicatoria.

Aunque no existe un flujo de trabajo perfecto para el análisis de tiempo hasta el evento, a continuación se incluye la plantilla general para crear y evaluar un modelo:

1. Examine los datos de entrada y decida qué variables explicativas utilizará. Elija las variables explicativas que sabe o espera que estén relacionadas con el tiempo de supervivencia y examínelas con gráficos. Los gráficos de dispersión de las variables explicativas en función del tiempo de supervivencia resultarán particularmente útiles al determinar las variables que están relacionadas con el tiempo de supervivencia (lamentablemente, solo pueden utilizarse las observaciones sin censurar para esto). Preste especial atención a los valores atípicos de las variables explicativas continuas y plantéese eliminarlos o aplicar una transformación logarítmica. En el caso de las variables categóricas, asegúrese de que haya varias observaciones sin censurar para cada categoría y, tal vez, combine o elimine las categorías con números reducidos de observaciones sin censurar.
2. Dependiendo de cómo se representen los datos, puede requerirse una cantidad considerable de ingeniería de datos para crear los campos de antigüedad e indicador de evento. Por ejemplo, es posible que necesite convertir los campos de fecha inicial y final en valores de antigüedad (para esto puede ser útil emplear la expresión DateDiff Arcade de la herramienta Calcular campo) o reclasificar un campo de texto en un campo indicador de evento binario.
3. Tras ejecutar la herramienta y revisar las advertencias o los errores, debería comprobar la precisión general del modelo y buscar indicios de un ajuste deficiente o de una mala especificación del modelo. Revise el histograma de residuales de desviación y preste especial atención a los valores residuales extremos (positivos o negativos) de las observaciones sin censurar. Evalúe el valor p y el índice de concordancia en la sección Resumen del modelo de los mensajes; si el valor p no es significativo (lo que ocurre rara vez), debería intentar encontrar variables explicativas que calculen mejor los tiempos de supervivencia. También debería valorar si el índice de concordancia es aceptablemente alto, lo que mantiene expectativas realistas.
4. Si el modelo general es lo suficientemente preciso, luego debería revisar las tablas de coeficientes de los mensajes para averiguar qué variables explicativas han repercutido en los tiempos de supervivencia y en qué medida. Plantéese eliminar cualquier variable explicativa que no sea estadísticamente significativa.
5. Para las entidades, luego examine la capa de entidades de salida de un mapa y busque patrones espaciales. ¿Algunas áreas tienen tiempos de supervivencia mayores que otras?
6. Por último, examine los gráficos emergentes y la tabla de atributos de observaciones de interés individuales para ver las curvas de supervivencia estimadas.

Referencias

Para implementar la herramienta, se utilizaron los siguientes recursos:

• Collett, David. 2023. "Modelling survival data in medical research." Chapman and Hall/CRC. https://doi.org/10.1201/9781003282525.
• Davidson-Pilon, Cameron. 2019. "lifelines: survival analysis in Python." Journal of Open Source Software. 4(40), 1317, https://doi.org/10.21105/joss.01317.
• Klein, John P. and Melvin L. Moeschberger. 2003. "Survival Analysis: Techniques for Censored and Truncated Data." Springer Science & Business Media. ISBN 0-387-95399-X.