Cálculos
La distancia estándar se proporciona como:
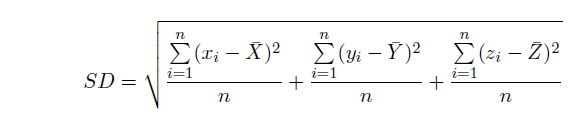
donde x i , y i y z i son las coordenadas para la entidad i , {x̄, ȳ, z̄} representa el centro medio para las entidades y n es igual a la cantidad total de entidades.
La distancia estándar ponderada se amplía a lo siguiente:
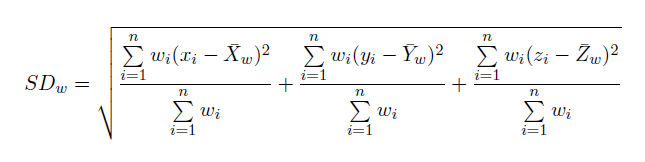
Donde wi es el peso en la entidad i y {x w, y w, z w} representa el centro medio ponderado.
Salida
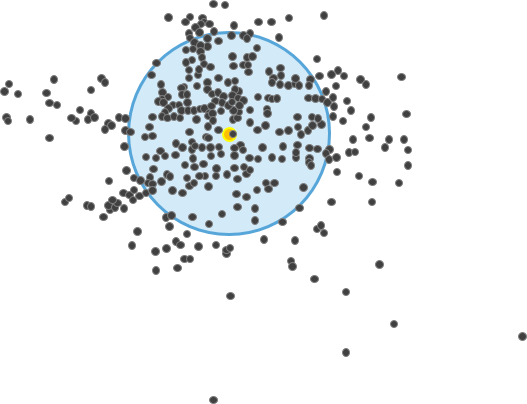
Aplicaciones potenciales
- Puede utilizar los valores de dos o más distribuciones para compararlos. Por ejemplo, un analista de delitos podría comparar la compactación de asaltos y de robos de automóviles. Tener conocimiento de cómo se distribuyen los diferentes tipos de delitos puede ayudar a la policía a desarrollar estrategias para combatir el delito. Si la distribución de delitos en un área en particular es compacta, estacionar un coche cerca del centro del área puede ser suficiente. Si la distribución es dispersa, el patrullaje de varios coches de la policía en el área puede ser más efectivo para responder a los delitos.
- También puede comparar el mismo tipo de entidad en distintos períodos de tiempo; por ejemplo, un analista de delitos puede comparar los robos que se producen de día y los que se producen de noche para ver si estos son más dispersos o más compactos durante el día que durante la noche.
- Además, puede comparar las distribuciones de las entidades con las entidades estacionarias. Por ejemplo, podría medir la distribución de las llamadas de emergencia durante varios meses para cada estación de bomberos que es responsable de responder en una región y compararlas para ver qué estaciones son responsables de responder en un área más amplia.
Recursos adicionales
Mitchell, Andy. La Guía de Esri para el análisis SIG, Volumen 2. Esri Press, 2005.