La herramienta Reducción de dimensión reduce el número de dimensiones de un conjunto de variables continuas agregando la mayor cantidad posible de varianza en menos componentes utilizando un Análisis de componentes principales (PCA) o un Análisis discriminante lineal (LDA) de rango reducido. Las variables se especifican como campos en una tabla o capa de entidades de entrada y los nuevos campos que representan las nuevas variables se guardan en la tabla o clase de entidad de salida. El número de campos nuevos será menor que el número de variables originales y mantendrá al mismo tiempo la cantidad de varianza más alta posible de todas las variables originales.
La herramienta Reducción de dimensión se utiliza normalmente para explorar relaciones multivariantes entre variables y para reducir el coste de cálculo de algoritmos de aprendizaje automático en los que la memoria requerida y el tiempo de procesamiento dependen del número de dimensiones de los datos. El uso de los componentes en lugar de los datos originales en análisis o algoritmos de aprendizaje automático puede proporcionar a menudo resultados comparables (o mejores) al tiempo que se consumen menos recursos de cálculo.
Se recomienda que utilice PCA cuando desea realizar un análisis o un método de aprendizaje automático en el que los componentes se utilizan para predecir el valor de una variable continua. Además, LDA requiere que cada registro se clasifique en una categoría, como una categoría de uso del suelo, y se recomienda que utilice LDA para realizar un análisis o un método de aprendizaje automático en el que los componentes se utilizan para clasificar la categoría de la variable de categorías en función de los campos de análisis numéricos.
Potenciales aplicaciones
Esta herramienta se puede utilizar en estos tipos de escenarios:
- Tiene una clase de entidad con muchos campos difíciles de visualizar simultáneamente. Al reducir el dataset a dos dimensiones, puede visualizar los datos utilizando un gráfico para ver interacciones multivariantes entre los campos en dos dimensiones.
- Desea utilizar herramientas de análisis del conjunto de herramientas Modelado de relaciones espaciales, como las herramientas Regresión lineal generalizada o Regresión ponderada geográficamente (GWR), pero muchos de los campos están altamente correlacionados entre sí. Al reducir el número de dimensiones de las variables explicativas, las herramientas de análisis pueden ser más estables y menos propensas a un exceso de ajuste en los datos de entrenamiento.
- Está realizando un método de aprendizaje automático cuyo tiempo de ejecución aumenta rápidamente con el número de variables de entrada. Al reducir el número de dimensiones, puede obtener resultados de análisis comparables utilizando menos memoria y un menor tiempo.
Cómo funciona PCA
PCA funciona creando secuencialmente componentes que capturan un determinado porcentaje de la varianza total de todos los campos de análisis. Cada componente en sí es una combinación lineal (suma ponderada) de cada uno de los campos de análisis, donde las ponderaciones se conocen como las cargas del componente. Junto con los campos de análisis, las cargas forman un eigenvector que indica la contribución de cada campo de análisis al componente. El componente también está asociado con un eigenvalor, que representa la varianza total mantenida por el componente.
Con dos campos de análisis, puede visualizar PCA geométricamente como ejes de rotación en el espacio de datos donde la rotación maximiza el ratio de variabilidad de los nuevos ejes, como se muestra en la siguiente imagen:
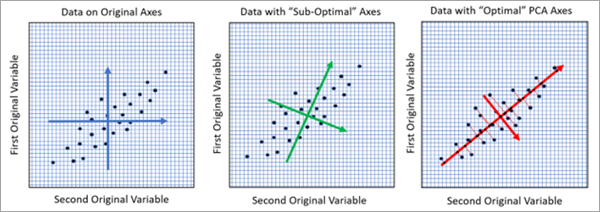
En la imagen de la izquierda, cada punto es un registro de la tabla de entrada que se representa en dos dimensiones con los valores de los dos campos de análisis en los ejes x e y. La longitud de los ejes azules representa la varianza de cada una de las dos variables. Las longitudes de las dos flechas azules son aproximadamente iguales, lo que indica que las dos variables tienen una varianza aproximadamente igual. En la imagen central, los ejes se han rotado para representar mejor la relación lineal entre las variables. Uno de los ejes verdes es ligeramente más largo que el otro, lo que indica más varianza en esa dirección. Sin embargo, esta rotación no es óptima. La imagen de la derecha muestra la rotación óptima encontrada por PCA que se alinea con la relación lineal entre las variables. Esta rotación produce un eje rojo con la mayor cantidad de varianza. El eje rojo más grande corresponde al primer componente principal y es la mejor representación en una sola dimensión de los datos bidimensionales. En las tres imágenes, la varianza total de las variables originales es la misma, pero la imagen de la derecha ha asignado la mayor cantidad posible de varianza al primer componente, lo que deja la menor cantidad posible de varianza restante para el segundo componente.
Puede ver los eigenvalores y eigenvectores para cada componente utilizando los parámetros Tabla de eigenvalores de salida y Tabla de eigenvectores de salida, y la tabla de eigenvectores viene con un gráfico de barras que muestra las cargas de cada componente. Para obtener los detalles matemáticos completos de PCA, consulte la sección Recursos adicionales.
Cómo funciona Análisis discriminante lineal de rango reducido
LDA (a menudo abreviado RR-LDA o LDA de rango reducido) funciona creando secuencialmente componentes que maximizan la separabilidad entre clases de una variable de categorías. El método tiene por objetivo reducir las dimensiones de los campos de análisis continuo y mantener al mismo tiempo la mayor precisión en la clasificación de la categoría de la variable de categorías. De forma similar a PCA, los componentes de LDA también están asociados con eigenvectores y eigenvalores para representar la contribución de los campos de análisis a cada componente y la cantidad de varianza mantenida por cada componente.
Para dos variables de análisis continuo y una variable de categorías con dos categorías, LDA también tiene una interpretación geométrica 2D que implica rotaciones. La siguiente imagen muestra un dataset, donde cada punto representa un registro del dataset de entrada. Los ejes x e y son los dos campos de análisis continuo, y los puntos se colorean en rojo o azul en función de su categoría. Las distribuciones roja y azul son las distribuciones de las categorías cuando se proyectan en el eje y. En las distribuciones de las clases existe cierta separabilidad, pero tienen una gran superposición y son difíciles de separar. Se produce una falta de separación similar al proyectar en el eje x.
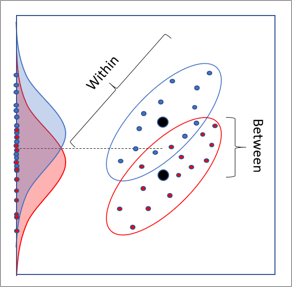
La siguiente imagen muestra la rotación de eje óptima determinada por LDA. Esta rotación da como resultado la mayor separación entre las distribuciones de las categorías, lo que permite la mayor tasa de clasificación de la categoría.
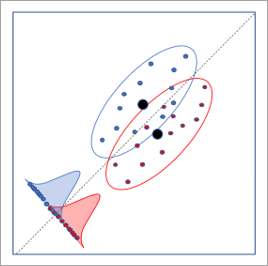
Si se crean al menos dos componentes, las entidades de salida incluyen un gráfico de dispersión Discriminante lineal. Los valores del primer y segundo componente se representan en los ejes y los puntos se colorean por categoría. Si los dos primeros componentes conservan suficiente información para diferenciar las categorías, los puntos del diagrama pueden agruparse por categoría.
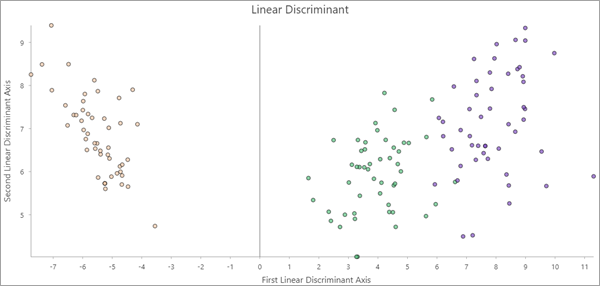
Puede ver los eigenvalores y eigenvectores para cada componente utilizando los parámetros Tabla de eigenvalores de salida y Tabla de eigenvectores de salida, y la tabla de eigenvectores incluye un gráfico de barras que muestra las cargas de cada componente. Para obtener los detalles matemáticos completos de LDA, consulte la sección Recursos adicionales.
Determinar el número de componentes
Una de las elecciones más importantes en la reducción de dimensión es cuántos componentes crear. Esto equivale a elegir cuántas dimensiones de los datos de entrada se van a reducir. En ocasiones, es posible que sepa cuántos componentes necesita en función del análisis previsto, por ejemplo, un método de aprendizaje automático que solo puede funcionar de manera eficiente con hasta cuatro variables. En otros casos, es posible que desee utilizar tantos componentes principales como sea necesario para mantener, por ejemplo, el 90 por ciento de la varianza total de los datos originales. En otras situaciones, es posible que necesite un equilibrio entre minimizar el número de componentes y maximizar el porcentaje de varianza que se mantiene.
En ambos métodos de reducción de datos, para los campos de análisis p, el porcentaje de varianza explicada por el componente número i es la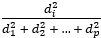 
, donde di es el eigenvalor del componente número i. Cada componente secuencial mantiene un porcentaje más pequeño de la varianza total que el componente anterior.
El número de componentes utilizados por la herramienta depende de si se especifican valores para los parámetros Número mínimo de componentes y Porcentaje mínimo de varianza a mantener.
- Si se especifica un parámetro y el otro no, el valor del parámetro especificado determina el número de componentes. El número de componentes es igual al número más bajo necesario para satisfacer el mínimo especificado.
- Si se especifican ambos parámetros, se utiliza el mayor de los dos números de componentes resultantes.
- Si no se especifica ninguno de los parámetros, el número de componentes se determina utilizando varios métodos estadísticos y la herramienta utiliza el mayor número de componentes recomendado por cada uno de los métodos. En ambos métodos de reducción de dimensión, los métodos incluyen el método Broken Stick y la prueba de esfericidad de Bartlett. En PCA, también se realiza una prueba de permutación si el valor del parámetro Número de permutaciones es mayor que cero. Los resultados de las pruebas estadísticas se muestran como mensajes de geoprocesamiento. Encontrará los detalles matemáticos de las tres pruebas en la sección Recursos adicionales.
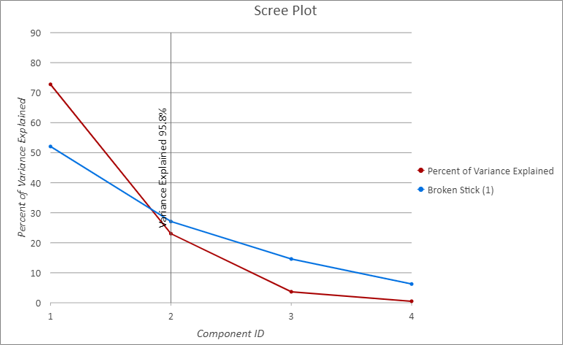
La tabla de eigenvalores de salida viene con un gráfico de líneas personalizado, denominado gráfico de sedimentación, para mostrar el porcentaje de varianza que mantiene cada componente. En el gráfico de sedimentación siguiente, el eje x muestra cada componente secuencial y la línea roja muestra el porcentaje de varianza explicada por cada componente. La línea roja disminuye, lo que indica que cada componente nuevo mantiene una cantidad menor de varianza que el componente anterior. La línea vertical negra sobre el componente 2 en el eje x indica que la herramienta utilizó dos componentes y que mantuvieron el 95,8 por ciento de la varianza total de las variables originales. La línea azul muestra los resultados del método Broken Stick, utilizado para estimar el número óptimo de componentes. El número óptimo de componentes a menudo corresponde al lugar donde se cruzan las líneas rojas y azules, lo que indica el acuerdo en el número de componentes.
Prácticas recomendadas y limitaciones
Plantéese lo siguiente al utilizar esta herramienta:
- En PCA, los resultados de este análisis dependen de si las variables se escalan. Dado que PCA divide la varianza total en componentes, cuanto mayor sea el tamaño de los valores sin procesar de un campo de análisis, mayor será el porcentaje de la varianza total asociada a él. Al escalar cada uno de los campos de análisis para que la varianza sea igual a uno, se elimina este efecto. Por ejemplo, si los campos de análisis están escalados, los datos medidos en pies y los datos medidos en metros dan como resultado los mismos componentes. Si no se escala, los datos medidos en pies contribuyen más al primer componente que los mismos datos en metros. Esto se debe a que un valor de distancia medido en pies es mayor que el mismo valor de distancia medido en metros (1 metro = 3,2808 pies).
- PCA estima eigenvalores y eigenvectores suponiendo relaciones lineales entre todos los campos de análisis. Si las relaciones entre los campos de análisis no son lineales, PCA no captura estas relaciones con precisión. Se recomienda crear una matriz de gráficos de dispersión de las variables de análisis y buscar patrones no lineales. Si se encuentran patrones no lineales, es posible que la herramienta Transformar campo pueda linealizar las relaciones.
Recursos adicionales
Para obtener más información sobre PCA y LDA de rango reducido, consulte la siguiente referencia:
- James, G., Witten, D., Hastie, T., Tibshirani, R. (2014). "An Introduction to Statistical Learning: with Applications in R." Springer Publishing Company, Incorporated. https://doi.org/10.1007/978-1-4614-7138-7
Para obtener más información sobre los métodos para determinar el número de componentes, consulte la siguiente referencia:
- Peres-Neto, P., Jackson, D., Somers, K. (2005). "How many principal components? Stopping rules for determining the number of non-trivial axes revisited." Computational Statistics & Data Analysis. 49.4: 974-997. https://doi.org/10.1016/j.csda.2004.06.015.