Cómo funciona la distribución direccional (Elipse de desviación estándar)

Mientras que puede obtener un sentido de la orientación al dibujar las entidades en un mapa, calcular la elipse de desviación estándar hace que la tendencia sea clara. Puede calcular la elipse de desviación estándar al utilizar las ubicaciones de las entidades o las ubicaciones influenciadas por un valor de atributo asociado con las entidades. El último se denomina elipse de desviación estándar ponderada.

Cálculos

La elipse de desviación estándar se proporciona como:

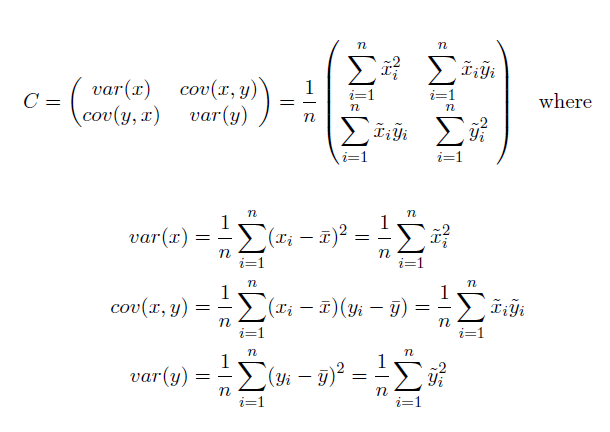
Donde x e y son las coordenadas para la entidad i, {x̄, ȳ} representa el centro medio para las entidades y n es igual a la cantidad total de entidades.

La matriz de covarianza de muestra se factoriza en un formulario estándar y la matriz se representa por sus valores y vectores eigen. De este modo, las desviaciones estándar para los ejes x e y son:

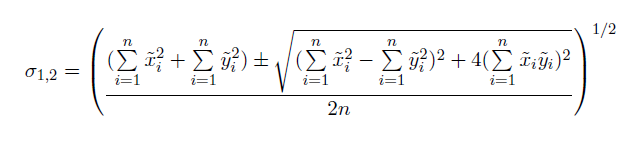
Consulte Recursos adicionales si desea obtener más información sobre los valores y vectores eigen.

Salida e interpretación

Para los datos bidimensionales, la herramienta Distribución direccional (Elipse de desviación estándar) crea una nueva clase de entidad que contiene un polígono elíptico centrado en el centro medio para todas las entidades (o para todos los casos donde se especifica un valor para el Campo de caso). Los valores de atributo para estos polígonos elipse de salida incluyen dos distancias estándar (ejes largo y corto); la orientación de la elipse y el campo de caso, si se especifican. La orientación representa la rotación del eje largo medido en el sentido de las agujas del reloj a partir del mediodía. También puede especificar la cantidad de desviaciones estándar a representar (1, 2 ó 3).

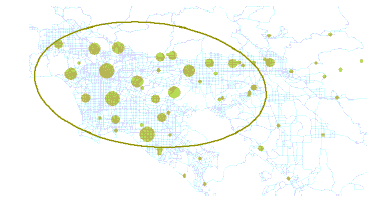
Aplicaciones potenciales

• La asignación de la tendencia distribucional a un conjunto de delitos puede identificar una relación a las entidades físicas particulares (una cadena de bares o restaurantes, un bulevar particular, y así sucesivamente).
• La asignación de muestras de agua subterránea a un contaminante particular puede indicar cómo se expande la toxina y, por consiguiente, puede resultar útil en la implementación de estrategias de mitigación.
• La comparación del tamaño, la forma y la superposición de elipses de varios grupos raciales o étnicos puede proporcionar ideas con respecto a la segregación racial o étnica.
• El gráfico de elipses para el brote de una enfermedad con el transcurso del tiempo se puede utilizar para modelar la extensión.
• Examinar la distribución de las elevaciones de las tormentas de una determinada categoría sería un factor muy útil a tener en cuenta al investigar la relación entre las condiciones atmosféricas y los accidentes aéreos.

Recursos adicionales

Chew, Victor. "Confidence, prediction, and tolerance regions for the multivariate normal distribution". Journal of the American Statistical Association 61.315 (1966): 605-617.

Fisher, N. I., T. Lewis, and B. J. J. Embleton. Statistical Analysis of Spherical Data. 1^st ed. Cambridge: Cambridge University Press, 1987. Cambridge Books Online. Web. 26 de abril de 2016.

Levine, Ned. "CrimeStat III: a spatial statistics program for the analysis of crime incident locations (version 3.0)." Houston (TX): Ned Levine & Associates/Washington, DC: National Institute of Justice (2004).

Mitchell, Andy. La Guía de Esri para el análisis SIG, Volumen 2. ESRI Press, 2005.

Wang, Bin, Wenzhong Shi, and Zelang Miao. (2015) Confidence Analysis of Standard Deviational Ellipse and Its Extension into Higher Dimensional Euclidean Space. PLoS ONE 10(3), e0118537.