La mayoría de las pruebas estadísticas comienzan al identificar una hipótesis nula. La hipótesis nula para las herramientas de análisis de patrón (conjunto de herramientas Análisis de patrones y conjunto de herramientas Asignación de clusters) es la Aleatoriedad espacial completa (CSR), ya sea de las entidades o de los valores asociados con esas entidades. Las puntuaciones z y los valores p devueltos por las herramientas de análisis de patrón le dicen si puede rechazar esa hipótesis nula o no. Por lo general, ejecutará una de las herramientas de análisis de patrón, con la esperanza de que la puntuación z y el valor p indiquen que puede rechazar la hipótesis nula, ya que indicaría que en lugar de un patrón aleatorio, sus entidades (o los valores asociados con las entidades) exhiben clusterig o dispersión estadísticamente significativa. La presencia de una estructura espacial, como el clustering, en el apaisado (o en los datos espaciales), significa que algunos procesos espaciales subyacentes están trabajando, y como geógrafo o analista de SIG, esto es por lo general lo que más le interesa.
El valor p es una probabilidad. Para las herramientas de análisis de patrón, existe la probabilidad de que el patrón espacial observado se haya creado mediante algún proceso aleatorio. Cuando el valor p es muy pequeño, significa que es muy poco probable (pequeña probabilidad) que el patrón espacial observado sea el resultado de procesos aleatorios, por lo tanto puede rechazar la hipótesis nula. Puede preguntar: ¿Cuán pequeño es suficientemente pequeño? Buena pregunta. Consulte la tabla y el análisis a continuación.
Las puntuaciones z son desviaciones estándar. Si, por ejemplo, una herramienta devuelve una puntuación z de +2,5, diría que el resultado son desviaciones estándar de 2,5 Tanto las puntuaciones z como los valores p se asocian con la distribución normal estándar como se muestra a continuación.
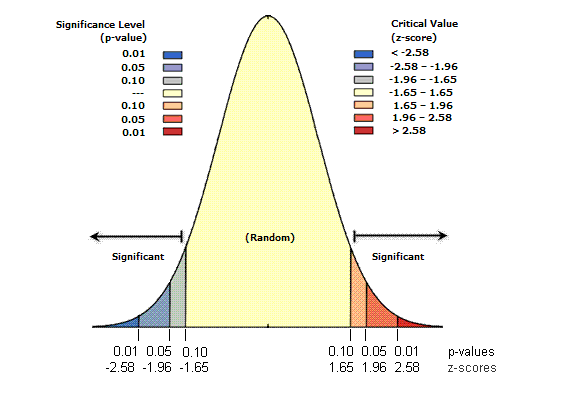
Las puntuaciones z muy altas o muy bajas (negativas), asociadas con valores p muy pequeños, se encuentran en las colas de la distribución normal. Cuando ejecuta una herramienta de análisis de patrón de entidad y produce valores p pequeños y una puntuación z muy alta o muy baja, esto indica que es poco probable que el patrón espacial observado refleje el patrón aleatorio teórico representado por su hipótesis nula (CSR).
Para rechazar la hipótesis nula, debe formar una opinión subjetiva con respecto al grado de riesgo que desea aceptar por estar equivocado (por rechazar falsamente la hipótesis nula). Por lo tanto, antes de ejecutar la estadística espacial, usted selecciona un nivel de confianza. Los niveles de confianza típicos son 90, 95 ó 99 por ciento. Un nivel de confianza del 99 por ciento sería el más conservador en este caso, lo que indica que no desea rechazar la hipótesis nula a menos que la probabilidad de que el patrón se haya creado mediante una opción aleatoria sea realmente pequeña (menos de 1 por ciento de probabilidad).
Niveles de confianza
En la tabla siguiente se muestran los valores p y las puntuaciones z críticas sin corregir para distintos niveles de confianza.
Nota:
Las herramientas que permiten aplicar el Índice de descubrimientos falsos (FDR) utilizarán valores p críticos corregidos. Estos valores críticos serán los mismos o inferiores a los que se muestran en la tabla siguiente.
| puntuación z (Desviaciones estándar) | valor P (Probabilidad) | Nivel de confianza |
|---|---|---|
< -1,65 o > +1,65 | < 0,10 | 90% |
< -1,96 o > +1,96 | < 0,05 | 95% |
< -2,58 o > +2,58 | < 0,01 | 99% |
Considere un ejemplo. Los valores de puntuación z críticos al utilizar un nivel de confianza del 95 por ciento son desviaciones estándar de -1,96 y +1,96. El valor p asociado sin corrección con un nivel de confianza del 95 por ciento es 0,05. Si su puntuación z está entre -1,96 y +1,96, su valor p sin corrección será mayor que 0,05, y no puede rechazar la hipótesis nula porque el patrón exhibido probablemente podría ser el resultado de procesos espaciales aleatorios. Si la puntuación z cae fuera de ese rango (por ejemplo, desviaciones estándar de -2,5 ó +5,4), probablemente sea muy poco común que el patrón espacial observado sea el resultado de la opción aleatoria, y el valor p será pequeño para reflejar esto. En este caso, es posible rechazar la hipótesis nula y seguir averiguando qué puede estar causando la estructura espacial estadísticamente significativa en los datos.
Una idea clave aquí es que los valores en el medio de la distribución normal (puntuaciones z como 0,19 ó 1,2, por ejemplo) representan el resultado esperado. Sin embargo, cuando el valor absoluto de la puntuación z es grande y las probabilidades son pequeñas (en las colas de la distribución normal), se detecta algo poco común y por lo general muy interesante. Para la herramienta Análisis de puntos calientes, por ejemplo, "poco común" significa un punto caliente estadísticamente significativo o un punto frío estadísticamente significativo.
Corrección FDR
Las herramientas de análisis de patrón espacial local, que incluyen Análisis de puntos calientes y Análisis de cluster y de valor atípico: I Anselin local de Moran proporcionan un parámetro booleano opcional Aplicar corrección False Discovery Rate (FDR). Cuando se marca este parámetro, el procedimiento Índice de descubrimientos falsos (FDR) reducirá potencialmente los umbrales de valor p críticos mostrados en la tabla anterior para dar cuenta de la realización de varias pruebas y la dependencia espacial. La reducción, si se produce, es una función del número de entidades de entrada y de la estructura de vecindad empleada.
Las herramientas de análisis de patrón espacial local funcionan teniendo en cuenta cada entidad en el contexto de las entidades de vecindad y determinando si el patrón local (una entidad de destino y sus vecinos) es estadísticamente distinta del patrón global (todas las entidades del dataset). Los resultados de la puntuación z y el valor p asociados con cada entidad determinan si la diferencia es estadísticamente significativa o no. Este enfoque analítico genera problemas relacionados tanto con las pruebas múltiples como la dependencia.
Múltiples pruebas: con un nivel de confianza del 95 por ciento, la teoría de la probabilidad deja claro que existen 5 posibilidades entre 100 de que un patrón espacial aparezca estructurado (agrupado o disperso, por ejemplo) y que se asocie con un valor estadísticamente significativo, cuando en realidad los procesos espaciales subyacentes que promueven el patrón son de hecho aleatorios. En estos casos rechazaríamos la hipótesis nula CSR debido a los valores p estadísticamente significativos. A priori, cinco de cada 100 puede parecer un resultado discreto, pero no si se tiene en cuenta que las estadísticas espaciales locales realizan una prueba para cada entidad del dataset. Por ejemplo, si hay 10.000 entidades, se obtendrán al menos unos 500 resultados falsos.
Dependencia espacial: las entidades muy próximas tienden a ser similares. La mayoría de las veces los datos espaciales exhiben este tipo de dependencia. Sin embargo, muchas pruebas estadísticas requieren que las entidades sean independientes. Para las herramientas de análisis de patrones locales esto es así porque la dependencia espacial puede inflar artificialmente la importancia estadística. La dependencia estadística se agrava con las herramientas de análisis de patrones locales porque cada entidad se evalúa en el contexto de sus vecinos, y es probable que las entidades próximas entre sí compartan muchos de los mismos vecinos. Esta superposición acentúa la dependencia espacial.
Hay al menos tres estrategias para tratar con los problemas relacionados con las múltiples pruebas y la dependencia espacial. La primera estrategia consiste en pasar por alto el problema ya que la prueba individual realizada para cada entidad en el dataset debería tenerse en cuenta en aislamiento. Sin embargo, con esta estrategia es muy posible que algunos resultados estadísticamente significativos sean incorrectos (parecen importantes estadísticamente pero en realidad los procesos espaciales subyacentes son aleatorios). La segunda estrategia consiste en aplicar un procedimiento de múltiples pruebas clásicas, como las correcciones Bonferroni o Sidak. No obstante, estos métodos son demasiado conservadores. Si bien pueden reducir en gran medida el número de falsos positivos, también detectarán menos resultados estadísticamente significativos. La tercera estrategia consiste en aplicar la corrección FDR, que calcula el número de falsos positivos para un nivel de confianza determinado y ajusta el valor p crítico en correspondencia. Para este método, los valores p estadísticamente significativos se clasifican del menor (más potente) al mayor (más débil) y, en función del cálculo de falsos positivos, los más débiles se eliminan de la lista. Las entidades restantes con valores p estadísticamente significativos se identifican por medio de los campos Gi_Bin o COType en la clase de entidades de salida. Aunque están lejos de la perfección, las pruebas empíricas demuestran que el rendimiento de este método es mucho mejor que dar por hecho que cada prueba local se realiza de forma aislada, o que aplicar los tradicionales métodos de múltiples pruebas, de marcada tendencia conservadora. La sección de recursos adicionales ofrece más información acerca de la corrección FDR.
Hipótesis nula y estadística espacial
Varias estadísticas en la caja de herramientas Estadística espacial son técnicas de análisis de patrón espacial deductivas, incluida Autocorrelación espacial (I de Moran global), Análisis de cluster y de valor atípico (I Anselin local de Moran) y Análisis de puntos calientes (Gi* de Getis-Ord). Las estadísticas deductivas se basan en la teoría de la probabilidad. La probabilidad es una medida de posibilidad, y subyacer todas las pruebas estadísticas (ya sea directa o indirectamente) es un cálculo de probabilidad que evalúa el rol de la posibilidad en el resultado del análisis. Típicamente, con las estadísticas tradicionales (no espaciales), usted trabaja con una muestra aleatoria y trata de determinar la probabilidad de que los datos de muestra sean una buena representación (sean reflexivos) de la población en general. Por ejemplo, puede preguntar "¿Cuáles son las posibilidades de que los resultados de mi sondeo de salida (que muestran que el candidato A vencerá al candidato B por un pequeño margen) reflejen los resultados de la elección final?" Pero con varias estadísticas espaciales, incluidas las estadísticas de tipo autocorrelación espacial que se enumeran más arriba, con frecuencia trata con todos los datos disponibles para el área de estudio (todos los delitos, todos los casos de enfermedad, los atributos para cada bloque censal, etc.). Cuando calcula la estadística para toda la población, ya no tiene una estimación. Tiene un hecho. Por consiguiente, ya no tiene sentido hablar sobre posibilidades o probabilidades. Por lo tanto, ¿de qué manera las herramientas de análisis espacial, aplicadas con frecuencia a todos los datos en el área de estudio, pueden informar legítimamente las probabilidades? La respuesta es que pueden hacerlo al postular, a través de la hipótesis nula, que los datos son, en realidad, parte de alguna población más grande. Considere esto con más detalle.
La hipótesis nula de aleatorización: donde sea apropiado, las herramientas en la caja de herramientas Estadística espacial utilizan la hipótesis nula de aleatorización como la base para la prueba de significancia estadística. La hipótesis nula de aleatorización postula que el patrón espacial observado de los datos representa una de las tantas ordenaciones espaciales posibles (n!). Si pudiera obtener los valores de los datos y arrojarlos en las entidades en su área de estudio, tendría una ordenación espacial posible de esos valores. (Tenga en cuenta que obtener los valores de los datos y arrojarlos arbitrariamente es un ejemplo de un proceso espacial aleatorio). La hipótesis nula de aleatorización establece que si pudiera hacer este ejercicio (obtenerlos, arrojarlos) infinitas veces, la mayoría del tiempo produciría un patrón que no sería muy distinto del patrón observado (los datos reales). De vez en cuando puede arrojar accidentalmente todos los valores más altos en la misma esquina de su área de estudio, pero la probabilidad de hacer eso es pequeña. La hipótesis nula de aleatorización establece que los datos son una de las tantas versiones posibles de la aleatoriedad espacial completa. Los valores de datos son fijos; solo la ordenación espacial podría variar.
La hipótesis nula de normalización: una hipótesis nula alternativa común, no implementada para la caja de herramientas Estadística espacial, es la hipótesis nula de normalización. La hipótesis nula de normalización postula que los valores observados derivan de una población de valores distribuida normalmente e infinitamente grande a través de algún proceso de muestreo aleatorio. Con una muestra diferente obtendría valores diferentes, pero aún esperaría que esos valores sean representativos de la distribución más grande. La hipótesis nula de normalización establece que los valores representan una de las tantas muestras de valores posibles. Si pudiera ajustar los datos observados a una curva normal y seleccionar aleatoriamente valores de esa distribución para arrojarlos a su área de estudio, la mayoría del tiempo produciría un patrón y una distribución de valores que no serían muy distintos del patrón/distribución observada (los datos reales). La hipótesis nula de normalización establece que los datos y la ordenación son una de las tantas muestras aleatorias posibles. Ni los valores de datos ni la ordenación espacial son fijos. La hipótesis nula de normalización solo es apropiada cuando los valores de datos se distribuyen normalmente.
Recursos adicionales
- Ebdon, David. Estadísticas en Geografía. Blackwell, 1985.
- Mitchell, Andy. La Guía de Esri para el análisis SIG, Volumen 2. Esri Press, 2005.
- Goodchild, M.F., Autocorrelación espacial. Catmog 47, Geo Books, 1986
- Caldas de Castro, Marcia, and Burton H. Singer. "Controlling the False Discovery Rate: A New Application to Account for Multiple and Dependent Test in Local Statistics of Spatial Association." Geographical Analysis 38, pp 180-208, 2006.