La herramienta Re-escalar por función re-escala los valores del ráster de entrada basándose en una función de transformación específica. Existen distintas funciones de transformación y cada una de ellas tiene formas de cálculo y aplicaciones distintas. Su elección depende de cuál es la función que mejor representa el fenómeno que se está estudiando. Puede refinar aún más las características de cada función a través de una serie de parámetros de entrada.
Con el fin de aprovechar al máximo la información de esta sección, le resultará útil familiarizarse con el vocabulario esencial que se utiliza en esta herramienta. Para entender cómo afectan los umbrales inferior y superior de la función de transformación a los valores de salida, consulte Efecto de los umbrales inferior y superior sobre los valores de salida.
Lista de funciones
La tabla siguiente proporciona un resumen de cada función, con enlaces que le llevarán al análisis específico de esa función.
Se utiliza cuando la preferencia aumenta con un aumento de los valores de entrada y la preferencia aumenta más rápidamente a medida que aumentan los valores de entrada. | |
Se utiliza cuando la preferencia máxima está alrededor de cierto valor de entrada y la preferencia decrece a medida que los valores de entrada se alejan de ese valor. | |
Se utiliza para indicar que los valores de entrada tienen una preferencia mayor. | |
Re-escala los valores de entrada utilizando una función lineal. | |
Se utiliza cuando la preferencia de los valores de entrada menores aumenta rápidamente a medida que los valores aumentan y se reduce cuando los valores de entrada siguen aumentando. | |
Se utiliza cuando los valores de entrada pequeños son la opción preferida. A medida que los valores aumentan, las preferencias decrecen rápidamente hasta que, con valores de entrada mayores, se reducen. | |
Se utiliza cuando los valores de entrada grandes son los preferidos. A medida que los valores aumentan, las preferencias aumentan rápidamente hasta que, con valores de entrada mayores, se reducen. | |
Re-escala los datos de entrada basándose la media y la desviación estándar de tal modo que los valores mayores del ráster de entrada tienen la preferencia mayor. | |
Re-escala los datos de entrada basándose la media y la desviación estándar de tal modo que los valores mayores del ráster de entrada tienen la preferencia menor. | |
Se utiliza cuando los valores de entrada próximos al punto medio tienen mayor preferencia. | |
Se utiliza cuando la preferencia de los valores de entrada aumenta rápidamente cuando los valores de entrada aumentan. | |
Se utiliza para indicar que los valores menores del ráster de entrada tienen mayor preferencia. | |
Se utiliza cuando hay un valor específico de entrada que es el más preferido y la preferencia decrece linealmente a medida que los valores de entrada se alejan del punto. |
Descripciones generales e ilustraciones de las funciones
A continuación para cada función se muestran una descripción general, un caso de uso y los detalles de los efectos que tienen ciertos parámetros de entrada sobre la curva de la función.
Información general
La descripción general contiene las propiedades básicas, así como los comportamientos específicos de cada función.
Caso de uso
El caso de uso describe un ejemplo específico del mundo real para el que esa función en particular puede ser adecuada.
Efectos de los parámetros
Esta sección describe de qué modo influyen los parámetros que controlan la forma en la función. Describe cómo influye en la curva las variaciones de los parámetros y muestra un gráfico con distintos valores de los parámetros para ilustrar los efectos. También incluye una expresión de clase de Python que demuestra cómo se ha construido la función de transformación que se muestra en los gráficos.
Nota:
Para cada ejemplo de gráfico mostrado, la entrada es un ráster cuyos valores oscilan entre 0 y 500. No hay ninguna razón específica para esta selección en particular, pero se utiliza de manera coherente en todos los gráficos para facilitar las comparaciones. En la práctica, los rásteres de entrada reales pueden tener valores de entrada en cualquier rango.
Función Exponencial
Información general
La función Exponencial transforma los datos de entrada aplicando una función exponencial con un factor de base y un desplazamiento especificados. En un modelo de adecuación, esta función es idónea cuando las ubicaciones con valores de entrada menores son las menos preferidas, pero las preferencias aumentan rápidamente en las ubicaciones con valores mayores.
Caso de uso
Analice cómo volvería a medir la distancia desde las fuentes de agua para un modelo de adecuación para tortugas. Las tortugas prefieren ubicaciones próximas al agua debido a su movilidad limitada. La preferencia por las ubicaciones próximas al agua decrece rápidamente al aumentar la distancia.
Efectos de los parámetros
Desplazamiento de entrada
El Desplazamiento de entrada es el valor que se resta de los valores de entrada. La función Exponencial se aplica a los valores de entrada desplazados para determinar los valores de la función.
Factor base
El parámetro Factor base controla cuán deprisa aumenta la función exponencial. A medida que el factor de base aumenta, la preferencia por los valores de entrada menores aumenta más lentamente a medida que los valores e entrada aumentan y después la preferencia aumenta rápidamente con los valores de entrada. Variar este parámetro puede ser útil si el rango de los datos de entrada es pequeño (por ejemplo, de 0 a 1) y se desea mantener una curva exponencial entre los valores mínimo y máximo.
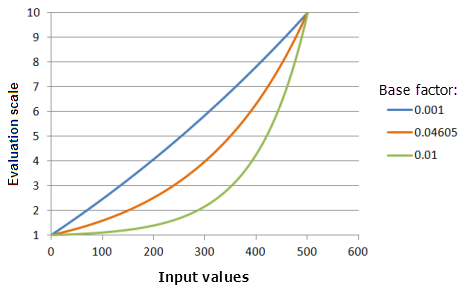
Función utilizada para el gráfico anterior:
- TfExponential(0.002651, BaseFactor, 0, 1, 500, 10)
Donde los valores usados para BaseFactor son: 0,001, 0,04605 y 0,01. Los valores de Valor constante 0,002651 y Factor base 0,04605 son los valores predeterminados de los parámetros correspondientes al dataset de entrada en el rango de 0 a 500.
Función Gaussiano
Información general
La función Gaussiano transforma los valores de entrada utilizando una distribución normal. Al aplicar una escala de evaluación creciente, el punto medio de la distribución normal define el valor más preferido. Si el punto medio está entre los umbrales inferior y superior, un valor de entrada igual al punto medio se asignará al valor Escala Hasta. El resto de valores de entrada decrece en la escala de evaluación (la preferencia decrece) a medida que los valores se desvían del punto medio en ambos sentidos hasta que alcanzan el valor de Escala Desde. En un modelo de adecuación, esta función resulta especialmente útil cuando la máxima preferencia está alrededor de un valor conocido y la preferencia decrece a medida que los valores de entrada se alejan de este valor.
Caso de uso
Al instalar paneles solares, seleccionar la dirección correcta para orientar los paneles es importante para lograr el mejor resultado. Para el hemisferio norte, el aspecto orientado al sur (180 grados) tiene la máxima preferencia. La preferencia de los aspectos cada vez más orientados hacia el este u oeste disminuye continuamente hasta que los aspectos orientados al norte son los menos preferidos.
Efectos de los parámetros
Punto medio
El parámetro Punto medio define el centro de la curva de Gauss. Tal vez desee desplazar el punto medio de la función respecto del punto medio de los datos de tal modo que los valores mayores o menores sean más o menos importantes. Un segundo motivo para desplazar el punto medio sería ajustar la función a valores del criterio fuera del intervalo de datos.
El punto medio puede controlar el rango de valores de entrada sobre los cuales se extiende la curva de la función.
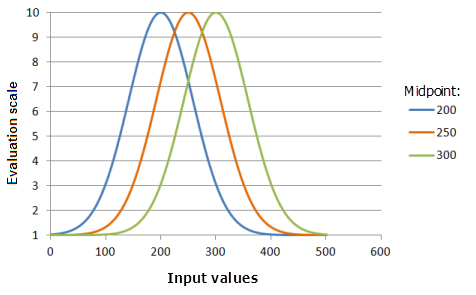
Función utilizada para el gráfico anterior:
- TfGaussian(Midpoint, 0.000147, 0, 1, 500, 10)
Donde los valores usados para Midpoint) son: 200, 250 y 300. Los valores Punto medio 250 y Expandir 0,0000147 son los valores predeterminados de los parámetros para el dataset de entrada en el rango de 0 a 500.
Expandir
El parámetro Expandir controla con qué rapidez se produce el decaimiento desde el punto medio. Cuanto mayor es el valor, más estrecha es la curva alrededor del punto medio (la preferencia decrece más rápidamente).
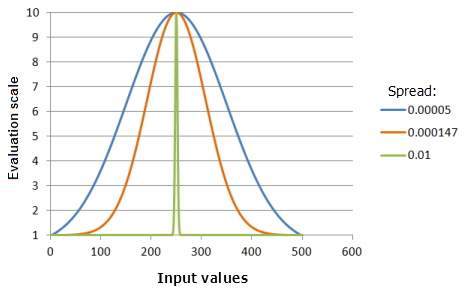
Función utilizada para el gráfico anterior:
- TfGaussian(250, Spread, 0, 1, 500, 10)
Donde los valores usados para Spread son: 0,00005, 0,000147 y 0,01. Los valores Punto medio 250 y Expandir 0,0000147 son los valores predeterminados de los parámetros para el dataset de entrada en el rango de 0 a 500.
Función Grande
Información general
La función de transformación Grande se utiliza cuando los valores de entrada grandes son los preferidos. El punto medio definido identifica el punto de transición de la función. Los valores mayores que el punto medio tienen una preferencia creciente y los valores por debajo del punto medio tienen una preferencia decreciente. La velocidad con la que los valores crecen o decrecen al alejarse del punto medio se determina mediante el parámetro de control de forma Expandir.
Caso de uso
Para crear un modelo de adecuación de comercialización de productos básicos tal vez deba re-escalar el criterio de rendimiento del café. Las ubicaciones con mayor rendimiento son preferibles, de modo que la preferencia aumenta de forma no lineal con el valor del rendimiento.
Efectos de los parámetros
Punto medio
El parámetro Punto medio define el punto de transición de la función. Si se desplaza para que esté por debajo del punto medio de los datos de entrada, el punto de transición varía de tal modo que el rango de los valores mayores tiene mayor preferencia a la derecha del punto medio y la preferencia aumenta más rápidamente.
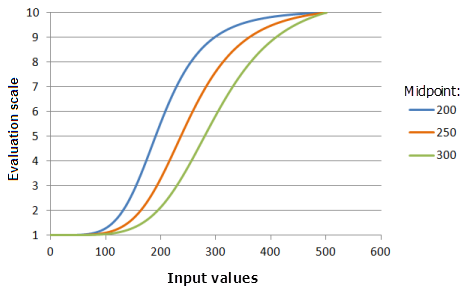
Función utilizada para el gráfico anterior:
- TfLarge(Midpoint, 5, 0, 1, 500, 10)
Donde los valores usados para Midpoint son: 200, 250 y 300. Los valores Punto medio 250 y Expandir 5 son los valores predeterminados de los parámetros para el dataset de entrada en el rango de 0 a 500.
Expandir
El parámetro Expandir controla la velocidad con la que crece y decrece la preferencia. A medida que el valor de Expandir aumenta, la preferencia de los valores de entrada mayores que el punto medio aumentará más rápidamente hasta el umbral superior, y la preferencia de los valores de entrada menores que el punto medio decrecerá más rápidamente hacia el umbral inferior.
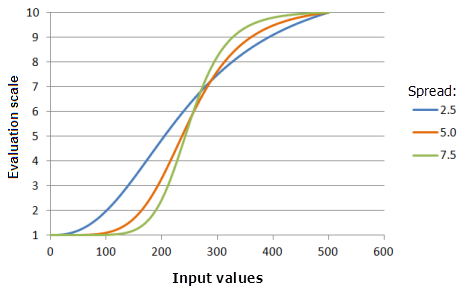
Función utilizada para el gráfico anterior:
- TfLarge(250, Spread, 0, 1, 500, 10)
Donde los valores usados para Spread son: 2,5, 5,0 y 7,5. Los valores Expandir 5 y Punto medio 250 son los valores predeterminados de los parámetros para el dataset de entrada en el rango de 0 a 500.
Función Lineal
Información general
La función de transformación Lineal aplica una función lineal entre los valores mínimos y máximos especificados. Si Escala Desde es mayor que Escala Hasta, se establece una relación lineal negativa (una pendiente negativa).
Esta función es idónea cuando la preferencia por los valores crece o decrece de forma lineal.
Caso de uso
Para crear un modelo de adecuación al cambio climático para un hábitat natural, tal vez sea interesante re-escalar la preferencia de la fauna salvaje por los valores de elevación. Dentro del área de estudio, serán preferibles los valores de elevación mayores.
Efectos de los parámetros
Mínimo
El parámetro Mínimo establece el primer punto por el cual debe pasar la función Lineal. El valor del parámetro se puede cambiar del mínimo de los datos de entrada para que se corresponda con la preferencia del fenómeno por el criterio.
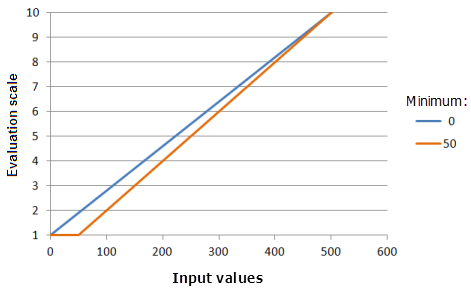
Función utilizada para el gráfico anterior:
- TfLinear(Minimum, 500, 0, 1, 500, 10)
Donde los valores usados para Minimum son: 0 y 50. Los valores Mínimo 0 y Máximo 500 son los valores predeterminados de los parámetros para el dataset de entrada en el rango de 0 a 500.
Máximo
El parámetro Máximo establece el segundo punto por el cual debe pasar la función Lineal. El valor del parámetro se puede cambiar del máximo de los datos de entrada para que se corresponda con la preferencia del fenómeno por el criterio.
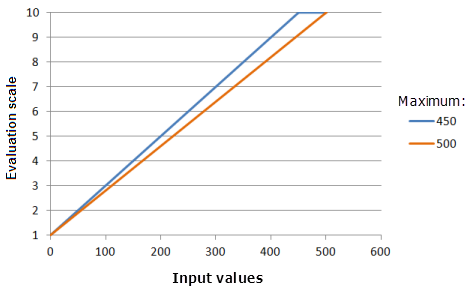
Función utilizada para el gráfico anterior:
- TfLinear(0, Maximum, 0, 1, 500, 10)
Donde los valores usados para Maximum son: 450 y 500. Los valores Mínimo 0 y Máximo 500 son los valores predeterminados de los parámetros para el dataset de entrada en el rango de 0 a 500.
Función Logaritmo
Información general
La función de transformación Logaritmo aplica una función logarítmica a los datos de entrada utilizando un desplazamiento y un factor especificados. En un modelo de adecuación, la función Logaritmo se utiliza mejor cuando las preferencias aumentan o disminuyen rápidamente y después desaparecen con el aumento de los valores del criterio de entrada.
Caso de uso
Para crear un modelo de adecuación para pájaros, puede ser interesante re-escalar el criterio de cantidad de alimento. La preferencia por localizaciones con poco alimento es la menor posible si no es suficiente para la población de pájaros. Si hay alimento suficiente para sobrevivir, la preferencia aumenta rápidamente en las ubicaciones con cantidades mayores de comida, ya que los pájaros estarán en mejor condición física. En cierto punto, los pájaros tendrán alimento suficiente, así que las ubicaciones donde el alimento sea todavía más abundante serán más deseables pero con un ritmo de crecimiento menor.
Efectos de los parámetros
Valor constante
Valor constante es el valor que se resta de los valores de entrada que permite controlar el valor de entrada inicial para calcular los logaritmos. Por ejemplo, en el caso de los pájaros, si los pájaros no pueden vivir en lugares con menos de 250 unidades de alimento, seguramente será interesante desplazar el punto de inicio de la función a 250.
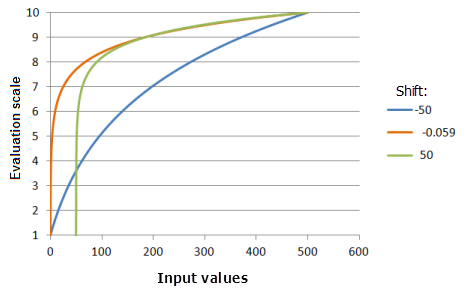
Función utilizada para el gráfico anterior:
- TfLogarithm(Shift, 0.0046, 0, 1, 500, 10)
Donde los valores usados para Shift son: -50,0, -0,059 y 50,0. Los valores Valor constante -0,059 y Exponente 0,0046 son los valores predeterminados de los parámetros para el dataset de entrada en el rango de 0 a 500.
Factor
Factor es un multiplicador que controla el aumento de la función logarítmica. Este parámetro se puede alterar si el rango de valores de entrada es pequeño (por ejemplo de 0 a 1) para mantener una curva logarítmica entre los valores mínimo y máximo.
Función Decaimiento logístico
Información general
La función de transformación Decaimiento logístico ajusta una función de decaimiento logístico con un mínimo y un máximo especificados utilizando un porcentaje de interceptación definido. En un modelo de adecuación, la función de decaimiento logístico resulta idónea cuando los valores de entrada menores son los preferidos. A medida que los valores de entrada aumentan, las preferencias decrecen rápidamente hasta un punto en el cual las preferencias mínimas se estabilizan para los valores de entrada mayores.
Caso de uso
Para crear un modelo de adecuación para viviendas, tal vez sea interesante re-escalar la distancia respecto a líneas eléctricas para el criterio de coste de la electricidad. Las localizaciones próximas a líneas eléctricas existentes son las preferidas porque costará menos dotarlas de electricidad. A cierta distancia, la preferencia decrece rápidamente porque es necesario instalar transformadores adicionales, lo cual aumenta los costes de equipos y mano de obra. La reducción en los niveles de preferencia lejos de las celdas ya no es tan visible ya que el coste adicional no afecta mucho a la preferencia una vez que la localización ya es demasiado cara.
Efectos de los parámetros
Mínimo
El parámetro Mínimo controla el punto de inicio del decaimiento logístico. Cuanto mayor es el valor mínimo, más rápidamente decrece la preferencia en la porción principal del decaimiento de la función (la curva será más abrupta).
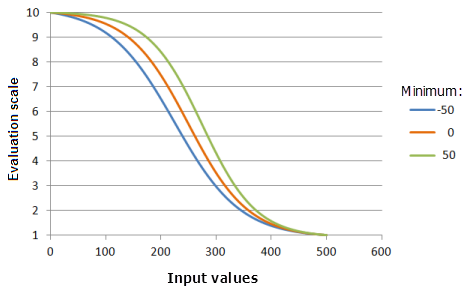
Función utilizada para el gráfico anterior:
- TfLogisticDecay(Minimum, 500, 99, 0, 1, 500, 10)
Donde los valores usados para Minimum son: -50, 0 y 50. Los valores Mínimo 0, y Máximo 500 y Porcentaje de interceptación Y 99 son los valores predeterminados de los parámetros para el dataset de entrada en el rango de 0 a 500.
Máximo
El parámetro Máximo controla el punto de fin del decaimiento logístico. Cuanto menor es el valor máximo, más rápidamente decrece la preferencia en la porción principal del decaimiento de la función (la curva será más abrupta).
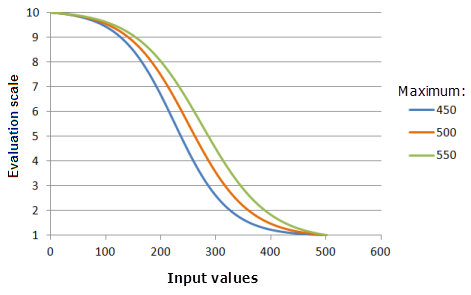
Función utilizada para el gráfico anterior:
- TfLogisticDecay(0, Maximum, 99, 0, 1, 500, 10)
Donde los valores usados para Maximum son: 450, 500 y 550. Los valores Mínimo 0, y Máximo 500 y Porcentaje de interceptación Y 99 son los valores predeterminados de los parámetros para el dataset de entrada en el rango de 0 a 500.
Porcentaje de interceptación Y
El parámetro Porcentaje de interceptación Y determina el rango de valores que queda en la parte de decaimiento de la curva Decaimiento logístico. Conceptualmente, podemos pensar en una función de decaimiento logístico como una forma de "S" al revés. Tiene dos colas conectadas por el cuerpo principal de la "S", que se llama la parte de decaimiento de la curva. Cuanto mayor es el valor de este parámetro, menor es el rango de valores de entrada que queda dentro de la porción de decaimiento de la curva (la "S" es más estrecha). La preferencia por los valores decrecerá más de prisa y la curva será más pronunciada.
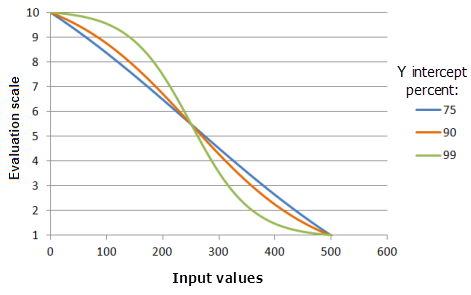
Función utilizada para el gráfico anterior:
- TfLogisticDecay(0, 500, YInterceptPercent, 0, 1, 500, 10)
Donde los valores usados para el porcentaje de interceptación Y son: 75, 90 y 99. Los valores Mínimo 0, y Máximo 500 y Porcentaje de interceptación Y 99 son los valores predeterminados de los parámetros para el dataset de entrada en el rango de 0 a 500.
Función Crecimiento logístico
Información general
La función de transformación Crecimiento logístico es parecida a la función de transformación Decaimiento logístico, salvo porque las preferencias en la función de crecimiento logístico crecen en lugar de decrecer.
Caso de uso
En un modelo de adecuación de hábitats, las preferencias de un animal aumentan logísticamente con el aumento del alimento disponible. Primero el alimento debe alcanzar un nivel crítico para la supervivencia y, a partir de ahí, la preferencia aumenta rápidamente con el aumento del alimento hasta que se alcanza el consumo máximo, lo cual hace que la preferencia ya no varíe.
Efectos de los parámetros
Mínimo
El parámetro Mínimo controla el punto de inicio del crecimiento logístico. Cuanto mayor es el valor mínimo, más rápidamente crece la preferencia en la porción principal del crecimiento de la función (la curva será más abrupta).
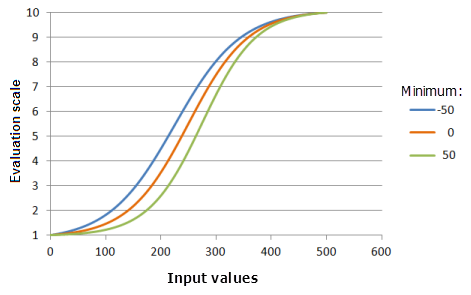
Función utilizada para el gráfico anterior:
- TfLogisticGrowth(Minimum, 500, 1, 0, 1, 500, 10)
Donde los valores usados para Minimum son: -50, 0 y 50. Los valores Mínimo 0, y Máximo 500 y Porcentaje de interceptación Y 1 son los valores predeterminados de los parámetros para el dataset de entrada en el rango de 0 a 500.
Máximo
El parámetro Máximo controla el punto de fin del crecimiento logístico. Cuanto menor es el valor máximo, más rápidamente crece la preferencia en la porción principal del crecimiento de la función (la curva será más abrupta).
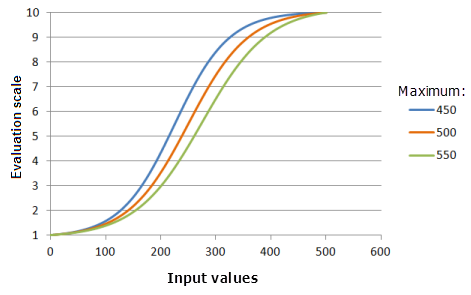
Función utilizada para el gráfico anterior:
- TfLogisticGrowth(0, Maximum, 1, 0, 1, 500, 10)
Donde los valores usados para Maximum son: 450, 500 y 550. Los valores Mínimo 0, y Máximo 500 y Porcentaje de interceptación Y 1 son los valores predeterminados calculados de los parámetros para el dataset de entrada en el rango de 0 a 500.
Porcentaje de interceptación Y
El parámetro Porcentaje de interceptación Y determina el rango de valores que queda en la parte de crecimiento de la curva Crecimiento logístico. Conceptualmente, podemos pensar en una función de crecimiento logístico como una forma de "S". Tiene dos colas conectadas por el cuerpo principal de la "S", que se llama la parte de crecimiento de la curva. Cuanto menor es el valor de Porcentaje de interceptación Y, menor es el rango de valores de entrada que queda dentro de la porción de crecimiento de la curva (la "S" es más empinada). La preferencia por los valores crecerá más de prisa y la curva será más pronunciada.
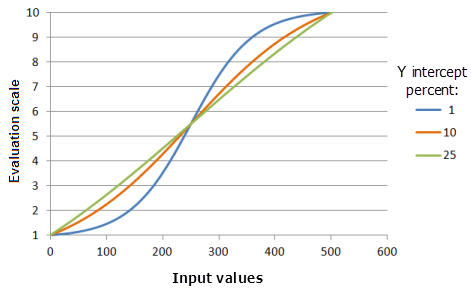
Función utilizada para el gráfico anterior:
- TfLogisticGrowth(0, 500, YInterceptPercent, 0, 1, 500, 10)
Donde los valores usados para el porcentaje de interceptación Y son: 1, 10 y 25. Los valores Mínimo 0, y Máximo 500 y Porcentaje de interceptación Y 1 son los valores predeterminados de los parámetros para el dataset de entrada en el rango de 0 a 500.
Función MSLarge
Información general
La función de transformación MSLarge es similar a la función Grande, excepto que la definición de la función está basada en multiplicadores especificados sobre la media y la desviación estándar. Por lo general, la diferencia entre las dos funciones es que la función MSLarge puede ser más adecuada cuando los valores preferidos son muy grandes.
El resultado puede ser parecido al de la función de transformación Grande con una combinación determinada de multiplicadores de media y desviación estándar.
Caso de uso
Similar al modelo de adecuación comercial de productos básicos analizado en el caso de usos de la función de transformación Grande, salvo en que las ubicaciones con una mayor producción de café tienen una preferencia mucho más alta en este caso.
Efectos de los parámetros
Multiplicador de valor medio
El parámetro Multiplicador de valor medio controla la pendiente de la curva de la función. A medida que el multiplicador decrece, el rango favorable de los valores mayores aumenta y, con los valores mayores, la curva de la función aumenta más rápidamente hacia el umbral superior.
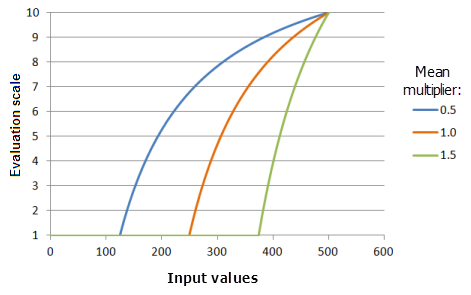
Función utilizada para el gráfico anterior:
- TfMSLarge(MeanMultiplier, 1, 0, 1, 500, 10)
Donde los valores usados para el valor medio son: 0,5, 1,0 y 1,5. El Multiplicador de valor medio 1 y el Multiplicador de desviación estándar 1 son los valores predeterminados de los parámetros para el dataset de entrada en el rango de 0 a 500.
Multiplicador de desviación estándar
El parámetro Multiplicador de desviación estándar controla la pendiente de la curva de la función. A medida que el multiplicador aumenta, la curva de la función aumenta más despacio.
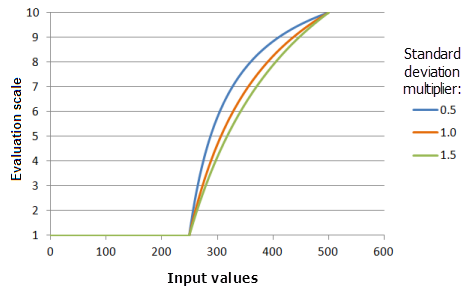
Función utilizada para el gráfico anterior:
- TfMSLarge(1, StandardDeviationMultiplier, 0, 1, 500, 10)
Donde los valores usados para la desviación estándar son: 0,5, 1,0 y 1,5. El Multiplicador de valor medio 1 y el Multiplicador de desviación estándar 1 son los valores predeterminados de los parámetros para el dataset de entrada en el rango de 0 a 500.
Función MSSmall
Información general
La función de transformación MSSmall es similar a la función Pequeño, excepto que la definición de la función está basada en factores sobre media y desviación estándar especificados. Por lo general, la diferencia entre las dos funciones es que la función MSSmall puede ser más adecuada cuando los valores preferidos son muy pequeños.
El resultado puede ser parecido al de la función de transformación Pequeño con una combinación determinada de multiplicadores de media y desviación estándar.
Caso de uso
De forma parecida al re-escalado de la distancia de las carreteras para el criterio del coste de la construcción en el modelo de adecuación de viviendas analizado en la función de transformación Pequeño, salvo en que las celdas más próximas tienen una preferencia mucho más alta en este caso.
Efectos de los parámetros
Multiplicador de valor medio
Multiplicador de valor medio: controla la pendiente de la curva de la función. A medida que aumenta el multiplicador, el rango favorable de los valores menores se incrementa y, con los valores mayores, la curva de la función disminuye más rápidamente hacia el umbral superior.
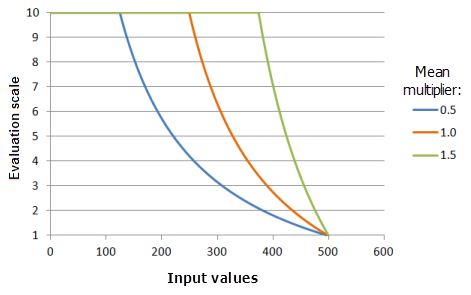
Función utilizada para el gráfico anterior:
- TfMSSmall(MeanMultiplier, 1, 0, 1, 500, 10)
Donde los valores usados para el valor medio son: 0,5, 1,0 y 1,5. El Multiplicador de valor medio 1 y el Multiplicador de desviación estándar 1 son los valores predeterminados de los parámetros para el dataset de entrada en el rango de 0 a 500.
Multiplicador de desviación estándar
El parámetro Multiplicador de desviación estándar controla la pendiente de la curva de la función. A medida que el multiplicador aumenta, la curva de la función decrece más despacio.
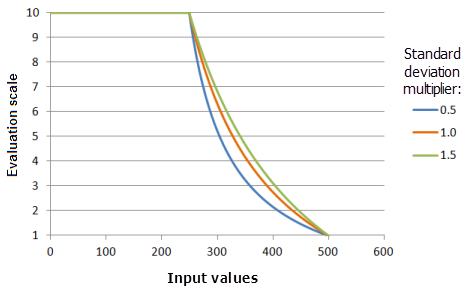
Función utilizada para el gráfico anterior:
- TfMSSmall(1, StandardDeviationMultiplier, 0, 1, 500, 10)
Donde los valores usados para la desviación estándar son: 0,5, 1,0 y 1,5. El Multiplicador de valor medio 1 y el Multiplicador de desviación estándar 1 son los valores predeterminados de los parámetros para el dataset de entrada en el rango de 0 a 500.
Función Cercano
Información general
La función de transformación Cercano es de la máxima utilidad cuando la preferencia más alta está alrededor de un valor específico. Si el punto medio está entre los umbrales inferior y superior, un valor de entrada igual al punto medio se asignará al valor Escala Hasta. El resto de valores de entrada decrece en la escala de evaluación (la preferencia decrece) a medida que los valores se desvían del punto medio en ambos sentidos hasta que alcanzan el valor de Escala Desde.
Las funciones Cercano y Gaussiano pueden ser similares según los parámetros especificados. Por lo general, la función Cercano decrece más rápidamente con una anchura más estrecha que la función Gaussiano. Por consiguiente se utiliza cuando los valores de entrada próximos al punto medio tienen mayor preferencia.
Caso de uso
De forma similar al modelo de adecuación de paneles solares analizado en la función de transformación Gaussiana, solo que en este caso la orientación hacia el sur es mucho más preferible que el resto.
Efectos de los parámetros
Punto medio
Punto medio: coincide con el punto medio de la función Gaussiano y define el centro de la curva de la función.
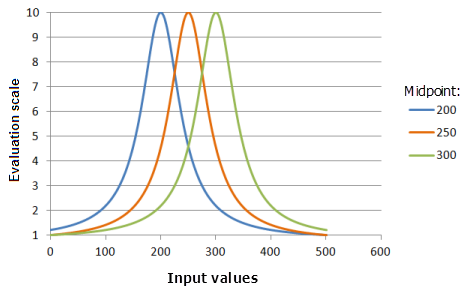
Función utilizada para el gráfico anterior:
- TfNear(Midpoint, 0.000576, 0, 1, 500, 10)
Donde los valores usados para Midpoint son: 200, 250 y 300. Los valores de Punto medio 250 y Expandir 0,000576 son los valores predeterminados de los parámetros para el dataset de entrada en el rango de 0 a 500.
Expandir
El parámetro Expandir es parecido a la función Gaussiano solo que con un efecto más drástico sobre los valores de entrada si se alejan del punto medio.
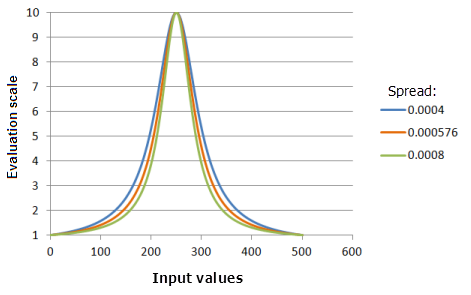
Función utilizada para el gráfico anterior:
- TfNear(250, Spread, 0, 1, 500, 10)
Donde los valores usados para Spread son: 0,0004, 0,000576 y 0,008. Los valores de Punto medio 250 y Expandir 0,000576 son los valores predeterminados de los parámetros para el dataset de entrada en el rango de 0 a 500.
Función Potencia
Información general
La función de transformación Potencia aplica una función potencia a los datos de entrada elevados a un exponente específico utilizando un desplazamiento definido. En un modelo de adecuación, la función Potencia resulta óptimo cuando los valores de entrada menores son los menos preferibles y mientras los valores de entrada aumentan las preferencias aumentan hasta alcanzar los valores de entrada mayores, para los cuales las preferencias aumentan rápidamente (este comportamiento depende del exponente).
Caso de uso
En un modelo de adecuación para situar una central nuclear puede ser adecuado re-escalar el criterio de seguridad basado en la distancia a los fallos. Las localizaciones más alejadas de una línea de falla aumentan continuamente en una función potencia basada en preferencias. Esto es, las ubicaciones más alejadas de la línea de falla son mucho más preferidas que las cercanas a la falla.
Efectos de los parámetros
Valor constante
El parámetro Valor constante es el valor que se resta de los valores de entrada que permite controlar el valor de entrada inicial para calcular las potencias. Por ejemplo, en el caso de uso de la central nuclear, se ha determinado que la planta no se debería construir a menos de 10 kilómetros de la línea de falla. Es posible que desee cambiar la función para que la función Potencia empieza en 10 kilómetros.
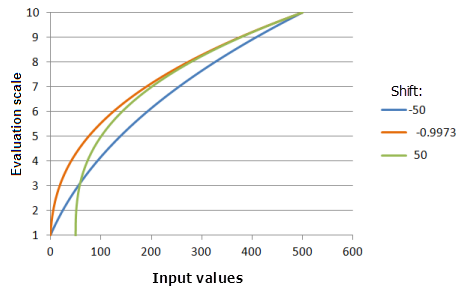
Función utilizada para el gráfico anterior:
- TfPower(Shift, 0.3704, 0, 1, 500, 10)
Donde los valores usados para Shift son: -50,0, -0,9973 y 50,0. Los valores de Valor constante -0,9973 y Exponente 0,3704 son los valores predeterminados de los parámetros para el dataset de entrada en el rango de 0 a 500.
Exponente
El parámetro Exponente controla cuán empinada es la función potencia. Cuanto mayor sea el exponente, más empinada será la curva de la función, especialmente con valores de entrada más grandes.
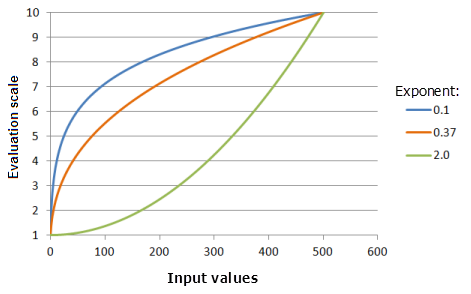
Parámetros de entrada del gráfico anterior:
- TfPower(-0.9973, Exponent, 0, 1, 500, 10)
Donde los valores usados para Exponent son: 0,1, 0,37 y 2,0. Los valores de Valor constante -0,9973 y Exponente 0,3704 son los valores predeterminados de los parámetros para el dataset de entrada en el rango de 0 a 500.
Función Pequeño
Información general
La función de transformación Pequeño se utiliza cuando los valores de entrada más bajos son los más preferidos. El punto medio definido identifica el punto de transición de la función. Los valores mayores que el punto medio tienen una preferencia decreciente y los valores por debajo del punto medio tienen una preferencia creciente. La velocidad con la que los valores crecen o decrecen al alejarse del punto medio se determina mediante el parámetro de control de forma Expandir.
Caso de uso
En un modelo de adecuación de vivienda tal vez interese re-escalar la distancia hasta el dataset de carreteras para tener en cuenta el criterio del coste de la construcción. Las localizaciones más próximas a las carreteras (los valores pequeños) tienen la máxima preferencia (costes mínimos) y los valores de las preferencias decrecen continuamente al aumentar la distancia a las carreteras.
Efectos de los parámetros
Punto medio
El parámetro Punto medio define el punto de transición de la función. Si se desplaza el punto medio para que esté por encima del punto medio de los datos de entrada, el punto de transición varía de tal modo que el rango de los valores menores tiene mayor preferencia a la izquierda del punto medio y la preferencia aumenta más lentamente.
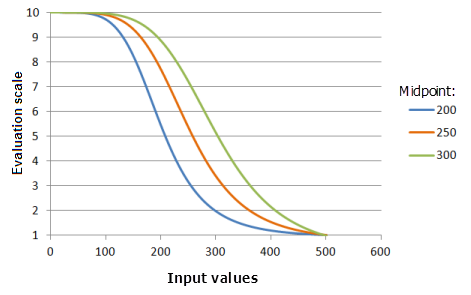
Función utilizada para el gráfico anterior:
- TfSmall(Midpoint, 5, 0, 1, 500, 10)
Donde los valores usados para Midpoint son: 200, 250 y 300. Los valores Punto medio 250 y Expandir 5 son los valores predeterminados de los parámetros para el dataset de entrada en el rango de 0 a 500.
Expandir
El parámetro Expandir controla la velocidad con la que decrece y crece la preferencia. A medida que el valor de Expandir aumenta, la preferencia de los valores de entrada menores que el punto medio aumentará más rápidamente hasta el umbral inferior, y la preferencia de los valores de entrada mayores que el punto medio decrecerá más rápidamente hacia el umbral superior.
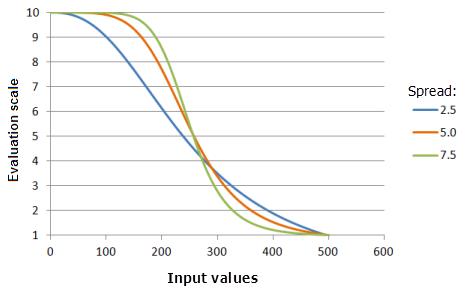
Función utilizada para el gráfico anterior:
- TfSmall(250, Spread, 0, 1, 500, 10)
Donde los valores usados para Spread son: 2,5, 5,0 y 7,5. Los valores Punto medio 250 y Expandir 5 son los valores predeterminados de los parámetros para el dataset de entrada en el rango de 0 a 500.
Función Lineal simétrica
Información general
La función de transformación Lineal simétrica aplica una función lineal entre los valores mínimo y máximo especificados que es simétrica respecto del punto medio entre Mínimo y Máximo. El valor de entrada correspondiente al punto simétrico tiene el valor de preferencia mayor, y la preferencia de los valores de entrada decrece linealmente al alejarse del punto reflejado. A todos los valores de entrada por debajo del Mínimo pero mayores que el Umbral inferior o por encima del Máximo pero menores que el Umbral superior se les asigna el valor de Escala Desde.
Si el Mínimo es mayor que el Máximo, se establece una relación lineal negativa (una pendiente negativa).
La función Lineal simétrica resulta idónea para los casos en los cuales la preferencia máxima está en el valor medio y las preferencias crecen y decrecen linealmente cuando los valores de entrada se alejan del punto medio.
Caso de uso
Cierto insecto transmisor de enfermedades tiene la mínima actividad a 70 grados Fahrenheit. A medida que la temperatura media crece o decrece hacia las temperaturas medias mínima y máxima del lugar de estudio, el insecto es más activo, lo cual da como resultado más casos de enfermedad entre humanos. Al localizar una instalación recreativa regional, las áreas con temperatura media de 70 (temperatura media) son las preferidas, con una preferencia que disminuye linealmente a medida que las temperaturas aumentan o se reducen con respecto a 70 grados hasta que se alcanzan las temperaturas promedio máxima y mínima en el área de estudio.
Efectos de los parámetros
Mínimo
El parámetro Mínimo establece uno de los puntos por los cuales debe pasar la función Lineal simétrica. Al cambiar el mínimo puede cambiar el punto medio donde la función tiene el eje de simetría. El valor del parámetro también se puede cambiar del mínimo de los datos del ráster de entrada para que se corresponda con la preferencia del fenómeno por el criterio.
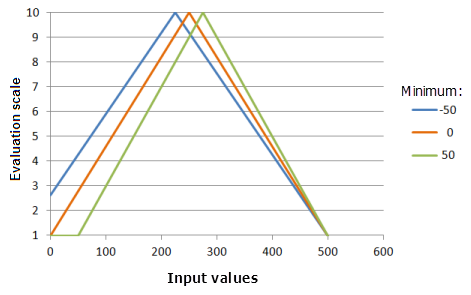
Función utilizada para el gráfico anterior:
- TfSymmetricLinear(Minimum, 500, 0, 1, 500, 10)
Donde los valores usados para Minimum son: -50, 0 y 50. Los valores Mínimo 0 y Máximo 500 son los valores predeterminados de los parámetros para el dataset de entrada en el rango de 0 a 500.
Máximo
Máximo: establece el segundo punto por el cual debe pasar la función Lineal simétrica. Al cambiar el máximo puede cambiar el punto medio donde la función tiene el eje de simetría. El valor del parámetro también se puede cambiar del máximo de los datos del ráster de entrada para que se corresponda con la preferencia del fenómeno por el criterio.
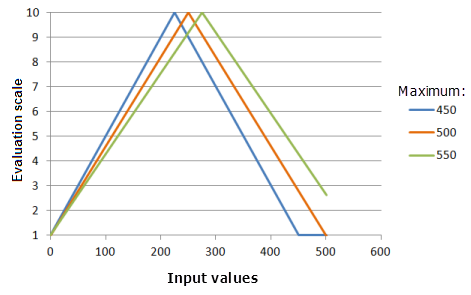
Función utilizada para el gráfico anterior:
- TfSymmetricLinear(0, Maximum, 0, 1, 500, 10)
Donde los valores usados para Maximum son: 450, 500 y 550. Los valores Mínimo 0 y Máximo 500 son los valores predeterminados de los parámetros para el dataset de entrada en el rango de 0 a 500.