Regresión ponderada geográficamente multiescala (MGWR)

La herramienta Regresión ponderada geográficamente multiescala (MGWR) realiza una técnica avanzada de regresión espacial que se utiliza en geografía, planeamiento urbanístico y otras disciplinas. Evolucionó a partir del modelo de Regresión ponderada geográficamente (GWR), que utiliza variables explicativas y dependientes dentro de la vecindad de una entidad de destino para construir un modelo de regresión lineal local para la interpretación o la predicción.

La motivación principal de GWR es que puede ser demasiado restrictivo para utilizar un único modelo de regresión para una gran región geográfica. En su lugar, GWR permite un modelo de regresión diferente en cada ubicación espacial, con los coeficientes de regresión que cambian suavemente sobre la región. Significa que, en distintas ubicaciones del área de estudio, las variables explicativas tienen diferentes impactos en la variable dependiente. GWR lo hace al crear un modelo de regresión ponderada para cada entidad espacial mediante las variables explicativas y dependientes de la entidad y sus vecinos espaciales. Los vecinos que están más cerca de la entidad reciben pesos más elevados y tienen mayor influencia en el modelo de regresión local.

La MGWR es una extensión de GWR que permite que la vecindad alrededor de cada entidad espacial varíe entre cada variable explicativa. Significa que, para algunas variables explicativas, la vecindad puede ser mayor o menor que para otras variables. Es importante permitir diferentes vecindades para distintas variables explicativas porque las relaciones entre las variables explicativas y la variable dependiente pueden operar en diferentes escalas espaciales: los coeficientes de algunas variables pueden cambiar gradualmente en el área de estudio, mientras que los coeficientes de otras variables cambian rápidamente. Hacer coincidir la vecindad de cada variable explicativa con la escala espacial de la variable explicativa es lo que permite que la MGWR calcule con mayor precisión los coeficientes del modelo de regresión local.

La MGWR ofrece resultados óptimos con los datasets grandes que contienen al menos cientos de entidades y datasets en los que la variable dependiente exhibe heterogeneidad espacial. Para modelar relaciones espacialmente variables de datasets más pequeños, pueden ser más apropiadas otras herramientas. La herramienta Regresión ponderada geográficamente multiescala (MGWR) actual solo acepta variables dependientes continuas. No ejecute el modelo con datos binarios ni de recuentos. Podría conducir a un modelo sesgado y resultados sin sentido.

Gran parte de este tema explicará la MGWR mediante comparaciones con otros métodos de regresión. Resulta útil tener conocimientos básicos de la regresión Mínimos cuadrados ordinarios (OLS) y familiarizarse con las vecindades, los esquemas de ponderación y los diagnósticos de GWR antes de continuar.

Más información sobre la regresión de OLS

Más información sobre la GWR

Selección del modelo de regresión

OLS, GWR y MGWR son todos ellos modelos de regresión lineal, pero operan en diferentes escalas espaciales y realizan diferentes suposiciones sobre la heterogeneidad espacial (la consistencia de las relaciones en el área de estudio) de un dataset. La OLS representa un modelo global. Se presupone que el proceso de generación de datos es estacionario en el espacio, de modo que un único coeficiente puede tener en cuenta la relación entre cada variable explicativa y la variable dependiente en cualquier lugar. La GWR representa un modelo local que suaviza la suposición de estacionariedad espacial al permitir que los coeficientes varíen en el espacio. Sin embargo, en la GWR, se presupone que todas las relaciones locales operan en la misma escala espacial al requerir que todas las variables explicativas utilicen la misma vecindad. Por ejemplo, si una variable explicativa utiliza 20 vecinos, todas las variables explicativas también deben utilizar 20 vecinos.

Sin embargo, la MGWR no solo permite que los coeficientes varíen en el espacio, sino que también permite que la escala varíe entre diferentes variables explicativas. La MGWR lo hace utilizando vecindades separadas para cada variable explicativa, para dar cuenta de diferentes escalas espaciales de las relaciones entre cada variable explicativa y la variable dependiente. Permite por tanto combinar variables explicativas que operan en escalas espaciales relativamente grandes, como la temperatura o la presión atmosférica, con variables que funcionan en escalas espaciales más pequeñas, como densidad de población o mediana de ingresos.

La MGWR estima coeficientes locales más precisos y experimenta menos problemas con la multicolinealidad que la GWR. Sin embargo, el tiempo de procesamiento es mucho más largo para MGWR que GWR, especialmente para las opciones Búsqueda dorada, Intervalos manuales o Definido por el usuario del parámetro Método de selección de vecindad. Estos tres métodos de selección de vecindad se basan en el algoritmo de ajuste de fondo, que requiere muchos cálculos y memoria. El tiempo de ejecución y el uso de memoria aumenta considerablemente a medida que aumenta el tamaño de los datos.

Al decidir qué modelo aplicar a los datos, tenga en cuenta estas preguntas:

• ¿Se debe ejecutar mi modelo a nivel local o global?
  • Si desea un modelo local, aplique la GWR o la MGWR. De lo contrario, utilice la OLS u otro modelo, por ejemplo, la herramienta Clasificación y regresión basadas en bosque.
• ¿Operan las variables explicativas de mi modelo en diferentes escalas espaciales?
  • Si sospecha que las variables explicativas pueden operar en diferentes escalas y desea identificar y modelar esas distintas escalas, aplique la MGWR.
• ¿Qué tamaño tiene mi dataset? ¿En cuánto tiempo necesito los resultados?
  • Si su dataset es muy grande y ejecuta la herramienta MGWR, la herramienta requiere un tiempo de ejecución más largo. Utilizando un hardware habitual de principios de la década de 2020 (16 procesadores lógicos y memoria de 32 GB) y parámetros típicos, en el caso de los datasets de más de 10.000 puntos, es probable que el tiempo de ejecución sea de varias horas. Con 50.000, el tiempo de ejecución probablemente será de varios días. Para 100.000 o más, es probable que ocurran errores de memoria.

Si tiene dudas de qué modelo local, GWR o MGWR aplicar a sus datos, comience con la MGWR. Al ejecutar la MGWR, también realiza una GWR con una configuración específica. En los mensajes de geoprocesamiento, puede buscar los diagnósticos de la GWR y compararlos con los diagnósticos de la MGWR. Otra posibilidad es ejecutar varias herramientas (OLS, GWR y MGWR) y utilizar el AICc enumerado en los mensajes de geoprocesamiento para comparar los modelos y elegir el mejor. Si decide ejecutar varias herramientas, puede escalar todos los modelos o dejar todos los modelos sin escala para garantizar que las salidas sean comparables.

Potenciales aplicaciones

La MGWR se puede aplicar a numerosos análisis y preguntas multivariante, como las siguientes:

• ¿Cómo influyen las distintas características, como el número de habitaciones, año de construcción, superficie de parcela, etc., en el precio de una vivienda? ¿Estas relaciones difieren significativamente entre las diferentes comunidades?
• ¿Cómo se asocia la distribución de PM2.5 a variables económicas como los ingresos por unidad familiar de la región, número de automóviles por hogar o porcentaje de producto interior bruto aportado por la agricultura?
• En la agricultura de precisión, ¿afectan las condiciones del suelo a la productividad de los cultivos en la misma escala espacial que variables atmosféricas como la temperatura, la humedad y las precipitaciones?

Consideraciones sobre el rendimiento y el punto de referencia

Son varios los factores que afectan al tiempo de ejecución de la MGWR. El factor más importante para el tiempo de ejecución es el número de entidades. El tiempo de ejecución aumenta cúbicamente con el número de entidades. La magnitud de la vecindad y el número de variables explicativas también afectan al tiempo de ejecución de la MGWR al requerir más cálculos para cada modelo local. Para calcular los resultados lo más rápido posible, la MGWR emplea el procesamiento en paralelo en su equipo. Algunos cálculos usarán todos los núcleos disponibles, pero otros se pueden controlar con el entorno Factor de procesamiento en paralelo.

Entradas de herramienta

Existen varios métodos para proporcionar la escala espacial de las variables explicativas.

Selección de vecindad (ancho de banda)

Una mejora clave de la MGWR es la posibilidad de variar el ancho de banda (vecindad) de cada variable explicativa en la ecuación de regresión lineal. La vecindad de una variable explicativa en una ubicación de destino incluye todas las ubicaciones que contribuirán a la estimación del coeficiente de la variable explicativa en el modelo de regresión lineal local. Cada vecindad se define por una cantidad de vecinos alrededor de la entidad de destino o por todos los vecinos dentro de una distancia fija. La cantidad de vecinos o la distancia pueden variar para cada variable explicativa.

Existen cuatro opciones para el parámetro Método de selección de vecindad que se pueden utilizar para estimar la escala espacial óptima para cada una de las variables explicativas:

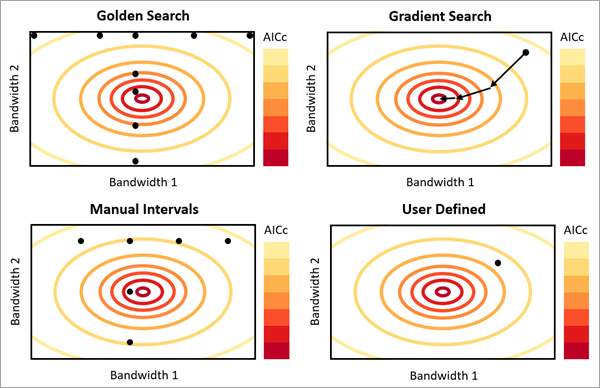
• Búsqueda dorada: determina el número de vecinos o la banda de distancia para cada variable explicativa utilizando el algoritmo Búsqueda dorada. Este método busca varias combinaciones de valores para cada variable explicativa entre un valor mínimo y un valor máximo especificados. El procedimiento es iterativo y utiliza los resultados de los valores anteriores para seleccionar cada nueva combinación que se va a probar. Los valores finales seleccionados tendrán el AICc más pequeño. Para la opción de número de vecinos, los valores mínimo y máximo se especifican utilizando los parámetros Cantidad mínima de vecinos y Cantidad máxima de vecinos. Para la opción de banda de distancia, los valores mínimo y máximo se especifican utilizando los parámetros Distancia mínima de búsqueda y Distancia máxima de búsqueda. Los valores mínimo y máximo se comparten para todas las variables explicativas, pero el número estimado de vecinos o bandas de distancia será diferente para cada variable explicativa (a menos que dos o más casualmente tengan la misma escala espacial). Esta opción es la que tarda más tiempo en calcularse, especialmente para datasets grandes o de alta dimensión.

• Búsqueda en gradiente: determina el número de vecinos o bandas de distancia para cada variable explicativa mediante un algoritmo de optimización basado en gradiente. Para hallar el ancho de banda óptimo de cada variable explicativa, Búsqueda en gradiente toma la derivada del AICc con respecto a los anchos de banda y actualiza los anchos de banda hasta que encuentra el AICc más bajo. Para la opción de número de vecinos, los valores mínimo y máximo se especifican utilizando los parámetros Cantidad mínima de vecinos y Cantidad máxima de vecinos. Para la opción Banda de distancia, los valores mínimo y máximo se especifican utilizando los parámetros Distancia mínima de búsqueda y Distancia máxima de búsqueda. Al igual que Búsqueda dorada, los valores mínimo y máximo se comparten para todas las variables explicativas, pero el número estimado de vecinos o la banda de distancia podría ser diferente para cada variable explicativa (a menos que dos o más casualmente tengan la misma escala espacial). Esta opción estima vecindades comparables con respecto a Búsqueda dorada, pero tiene un mejor rendimiento de tiempo de ejecución y requiere un uso significativamente menor de la memoria.

• Intervalos manuales: determina la cantidad de vecinos o bandas de distancia para cada variable explicativa incrementando el número de vecinos o bandas de distancia a partir de un valor mínimo. Para la opción de cantidad de vecinos, el método comienza con el valor del parámetro Cantidad mínima de vecinos. A continuación, la cantidad de vecinos aumenta según el valor del parámetro Incremento de número de vecinos. Este incremento se repite un determinado número de veces, especificado con el parámetro Número de incrementos. Para la opción de banda de distancia, el método utiliza los parámetros Distancia mínima de búsqueda, Incremento de distancia de búsqueda y Número de incrementos. El número de vecinos o bandas de distancia utilizado por cada variable explicativa será uno de los valores probados, pero los valores pueden ser diferentes para cada variable explicativa. Esta opción es más rápida que Búsqueda dorada y con frecuencia estima vecindades comparables.

• Definido por el usuario: el número de vecinos o bandas de distancia que utilizan todas las variables explicativas. El valor se especifica mediante el parámetro Cantidad de vecinos o Banda de distancia. Esta opción proporciona el máximo control si conoce los valores óptimos.

De forma predeterminada, los parámetros de vecindad dependiente de cada método de selección de vecindad se aplican a todas las variables explicativas. Sin embargo, solo es posible proporcionar unos parámetros de selección de vecindad personalizados para determinadas variables explicativas utilizando el correspondiente parámetro de invalidación para el tipo de vecindad y el método de selección: Cantidad de vecinos para Búsqueda dorada, Cantidad de vecinos para Búsqueda en gradiente, Cantidad de vecinos para Intervalos manuales, Cantidad de vecinos definida por el usuario, Distancia de búsqueda para Búsqueda dorada, Distancia de búsqueda para Búsqueda en gradiente, Distancia de búsqueda para Intervalos manuales o Distancia de búsqueda definida por el usuario. Para utilizar vecindades personalizadas para determinadas variables explicativas, proporcione las variables explicativas en la primera columna del correspondiente parámetro de invalidación correspondiente y proporcione las opciones personalizadas de la vecindad en las otras columnas. Las columnas tienen los mismos nombres que los parámetros que invalidan; por ejemplo, si utiliza intervalos manuales con banda de distancia, la columna Incremento de distancia de búsqueda especifica valores personalizados del parámetro Incremento de distancia de búsqueda. En el panel Geoprocesamiento, los parámetros de vecindad personalizada se encuentran en la categoría del parámetro Opciones de vecindad personalizada.

Por ejemplo, supongamos que utiliza tres variables explicativas con el tipo de vecindad Búsqueda dorada con mínimo de 30 vecinos y máximo de 40 vecinos. Si la herramienta se ejecuta con estos parámetros, cada una de las tres variables explicativas utilizará entre 30 y 40 vecinos. Si, en cambio, desea utilizar entre 45 y 55 vecinos solo para la segunda variable explicativa, puede proporcionar la segunda variable explicativa, el mínimo personalizado y el máximo personalizado en las columnas del parámetro Cantidad de vecinos para Búsqueda dorada. Con estos parámetros, la primera y la tercera variables explicativas utilizarán entre 30 y 40 vecinos, y la segunda variable explicativa utilizará entre 45 y 55 vecinos.

Esquema de ponderación local

La MGWR estima un modelo de regresión local para cada entidad de destino aplicando una función de ponderación geográfica (kernel) a la entidad y sus entidades vecinas. Los vecinos más cercanos a la entidad de destino tienen un mayor impacto en los resultados del modelo local. Las opciones kernel están disponibles en el parámetro Esquema de ponderación local: Gaussiano y Bicuadrado. Para obtener más información sobre la ponderación geográfica con kernels, consulte Cómo funciona Regresión ponderada geográficamente. En la MGWR, el ancho de banda de ponderación varía en las variables explicativas.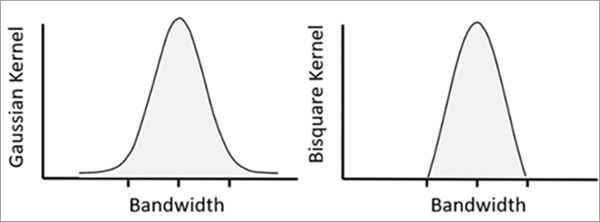

Nota:

El tipo de vecindad de búsqueda en gradiente solo permite el kernel bicuadrado. El kernel gaussiano se puede permitir en versiones futuras.

Datos escalados y coeficientes

De forma predeterminada, todas las variables explicativas y la variable dependiente se escalan para tener un valor medio igual a cero y una desviación estándar igual a uno (también denominada estandarización de puntuación z). Los coeficientes estimados de los valores de datos escalados se interpretan mediante desviaciones estándar; por ejemplo, un coeficiente de 1,2 significa que un aumento de la desviación estándar de la variable explicativa se correlaciona con un aumento de desviación estándar de 1,2 de la variable dependiente. Dado que todos los coeficientes utilizan una unidad común, los valores se pueden comparar directamente para ver qué variables explicativas suponen un mayor impacto en el modelo. Por lo general, se recomienda escalar las variables, y la escala es especialmente importante si el rango de valores de las variables varía considerablemente. Sin embargo, existe la opción de no escalar los datos desactivando el parámetro Escalar datos.

En la mayoría de los modelos de regresión lineal, como ocurre con la OLS y la GWR, los coeficientes no varían en la escala lineal. Significa que, si escala los datos de entrada, ajusta el modelo de regresión y, a continuación, desescala el resultado a las unidades originales, el resultado será el mismo que si no hubiera escalado los datos en absoluto. Sin embargo, en la MGWR, el escalado y el desescalado no darán lugar al mismo modelo que obtendría con los datos originales. Se debe a que el ajuste de fondo es un procedimiento iterativo en el que los resultados de cada paso dependen de los resultados de pasos anteriores. El uso de diferentes escalas de inicio afectará a la ruta de los valores probados y dará como resultado distintos modelos de MGWR. Por lo general, los resultados escalados son más precisos ya que el escalado ecualiza las varianzas de las variables, mientras que el procedimiento iterativo suele converger más rápido y a valores más exactos si cada variable contribuye en la misma medida a la varianza total de los datos. Si las variables explicativas presentan varianzas diferentes (por ejemplo, al tener diferentes unidades), las variables con varianzas más grandes tendrán una influencia mayor en cada paso de la estimación iterativa. En la mayoría de los casos, esta influencia afectará negativamente a los anchos de banda y coeficientes finales del modelo.

Para facilitar la interpretación de los resultados escalados, todos los coeficientes de las salidas de la herramienta contendrán un valor escalado y el valor sin escalar a las unidades de datos originales. Estas salidas contienen campos adicionales en las entidades de salida (también agregados como capas a la capa de grupo de salida) y rásteres adicionales en el directorio del parámetro Espacio de trabajo de ráster de coeficiente de salida. Al realizar predicciones de nuevas ubicaciones con los parámetros Ubicaciones de predicción y Entidades predichas de salida, todos los valores predichos se desescalan a las unidades de datos originales. Consulte Salidas de la herramienta para obtener más información sobre las salidas.

Salidas de la herramienta

La herramienta produce una variedad de salidas diferentes, incluida una capa de grupo para varios campos de las entidades, mensajes y gráficos de salida. Entre las salidas opcionales están una clase de entidad que predice valores en nuevas ubicaciones, una tabla de vecindad y superficies ráster de cada coeficiente.

Capas de grupo y simbología

La capa de simbología de salida predeterminada visualiza los residuales estandarizados de los modelos de regresión lineal local con un esquema de color clasificado. Examine los patrones de los residuales para determinar si el modelo está bien especificado. Los residuales de los modelos de regresión bien especificados se distribuirán normalmente y serán espacialmente aleatorios sin clustering de valores. Puede ejecutar la herramienta Autocorrelación espacial (I de Moran global) con los residuales de regresión para probar si son espacialmente aleatorios. Un clustering de residuales alto y bajo estadísticamente significativo indica que el modelo de MGWR no es óptimo.

Las capas del coeficiente y la significancia estadística de cada variable explicativa se agregan al mapa como una capa de grupo, con capas de subgrupo separadas para cada variable explicativa. Cada capa de coeficientes presenta un esquema de color divergente centrado en cero. Por tanto, es posible guiarse por los colores para identificar qué variables presentan relaciones positivas y negativas con la variable dependiente. Para los puntos, las entidades estadísticamente significativas (confianza del 95 por ciento) se indican con halos verdes alrededor de los puntos, y las relaciones no significativas se indican mediante halos grises. En el caso de los polígonos, las relaciones significativas se indican con mallas de textura en los polígonos. Examine las capas de coeficiente y las capas de significancia para comprender mejor la variación espacial de las variables explicativas. Puede utilizar sus perspectivas de esta variación espacial como fuente de información de sus políticas. Las políticas globales pueden funcionar bien si las variables son estadísticamente significativas a nivel mundial y exhiben poca variación regional, pero las políticas locales pueden funcionar mejor si hay una variación espacial sustancial en los coeficientes de regresión. En este caso, puede ser apropiado iniciar políticas en áreas donde el efecto local es positivo y grande. Sin embargo, es posible que las mismas políticas no sean adecuadas en otras áreas donde el efecto sea pequeño o negativo.

Mensajes y diagnósticos

Los mensajes proporcionan información sobre el modelo MGWR y su rendimiento. Los mensajes presentan varias secciones.

Estadísticas de resumen para estimaciones de coeficientes

La sección Resumen de estadísticas para estimaciones de coeficientes resume el valor medio, desviación estándar, mínimo, mediana y máximo de las estimaciones de coeficientes en toda el área de estudio. El valor medio de cada coeficiente refleja la asociación entre esa variable explicativa y la variable dependiente. La desviación estándar indica la variación espacial de cada variable explicativa. Una pequeña desviación estándar implica que un método más sencillo como OLS pueda modelar los datos adecuadamente. Si el parámetro Datos de escala está activado, puede comparar los valores de las distintas variables explicativas. Si el parámetro Datos de escala no está activado, el valor de los coeficientes entre variables explicativas no se puede comparar directamente porque las unidades pueden variar.

Diagnóstico de modelo

La sección Diagnóstico de modelo contiene una tabla que muestra varios diagnósticos de modelo para GWR y MGWR, incluidos R², R², AICc ajustado, varianza residual y número de grados de libertad efectivos. Para más información sobre estos diagnósticos de modelo, consulte Cómo funciona Regresión ponderada geográficamente.

Nota:

En algunos casos, el modelo GWR para su comparación puede no calcularse. En este caso, solo se muestran los diagnósticos para la MGWR.

Puede utilizar los diagnósticos R² y R² ajustado para evaluar la bondad de ajuste del modelo a los datos. Cuanto mayor sea el R2 y el R2 ajustado, mejor es el ajuste entre el modelo y los datos. Evalúe la complejidad del modelo mediante el número de variables explicativas y el valor de diagnóstico Grado de libertad efectivo. Los modelos más sencillos presentan un mayor grado de libertad efectivo y menos parámetros. Si un modelo presenta demasiados parámetros, corre riesgo de un exceso de ajuste en los datos. El diagnóstico AICc tiene en cuenta tanto la bondad de ajuste como la complejidad del modelo. La herramienta Regresión ponderada geográficamente multiescala selecciona el modelo que exhibe el AICc más bajo.

Resumen de variables explicativas y vecindades

La sección Resumen de variables explicativas y vecindades muestra los niveles estimados de vecindad y de significancia de cada variable explicativa. En el caso de las vecindades basadas en el número de vecinos, el número óptimo de vecinos se muestra como un recuento y como un porcentaje del número total de entidades de entrada. En el caso de las vecindades de banda de distancia, las bandas de distancia óptimas se muestran junto con la distancia como un porcentaje de la extensión diagonal de las entidades de entrada. Los porcentajes de las entidades o de la extensión son útiles a la hora de caracterizar la escala espacial de las variables explicativas; por ejemplo, si una variable explicativa utiliza como vecinos el 75 por ciento de las entidades, los modelos de regresión local están más cerca de los modelos globales que de los modelos locales (lo que indica que un modelo más sencillo como la OLS puede ser adecuado). Si otra variable explicativa utiliza como vecinos solo el 5 por ciento de las entidades de entrada, es un modelo más local. En todos los tipos de vecindad, se muestran el recuento y porcentaje de los modelos locales estadísticamente significativos con un nivel de confianza del 95 por ciento para cada variable explicativa.

Historial de búsqueda de anchos de banda óptimos

La sección Historial de búsqueda de anchos de banda óptimos muestra el historial de búsqueda de los anchos de banda óptimos, junto con el valor de AICc de cada conjunto de valores evaluados. La herramienta comienza a buscar el ancho de banda óptimo de cada variable explicativa asignando a todas las variables el mismo valor: el ancho de banda óptimo de GWR. A continuación, la herramienta ajusta el ancho de banda y el coeficiente de cada variable en cada iteración y estima un nuevo valor de AICc. A medida que avanzan las iteraciones, el valor de AICc disminuye hasta que se estabiliza o aumenta, y es aquí donde se da fin a las iteraciones. La opción Definido por el usuario es la que requiere generalmente el menor número de iteraciones, mientras que la opción Búsqueda dorada suele requerir más. Aunque utiliza un gran número de iteraciones, la opción Búsqueda en gradiente suele tener el tiempo de ejecución más rápido, ya que cada iteración se puede calcular rápidamente.

Nota:

Para la Búsqueda en gradiente con cantidad de vecinos, el valor AICc final que se muestra en la sección del historial de búsqueda de ancho de banda óptimo a menudo será ligeramente diferente al valor AICc que se muestra en la sección de diagnósticos de modelo. Sucede porque Búsqueda en gradiente utiliza una representación continua del número de vecinos durante la optimización del ancho de banda, que provoca pequeñas cantidades de imprecisiones en el valor AICc calculado de cada iteración. Al informar del AICc del modelo final, utilice el valor que se muestra en la sección de diagnósticos de modelo.

Resumen de estadísticas de ancho de banda

La sección Resumen de estadísticas de ancho de banda resume los valores que se utilizan para evaluar si cada variable explicativa es estadísticamente significativa en cada modelo local. Entre estas estadísticas están la vecindad óptima (número de vecinos o banda de distancia) de MGWR, el número efectivo de parámetros, el nivel de significancia ajustado (alfa) y el valor crítico ajustado de estadística seudo t. Estos valores se utilizan para crear los campos relacionados con la significancia estadística de cada variable explicativa en las entidades de salida. El valor ajustado de alfa se calcula dividiendo el nivel de significancia (0,05) entre el número efectivo de parámetros; de este modo, se controla la tasa de error por familia (FWER) de la significancia de las variables explicativas. El valor alfa ajustado se utiliza como nivel de significancia en una evaluación t de dos lados con el número efectivo de grados de libertad.

Entidades de salida

La herramienta genera una clase de entidad que abarca diagnósticos locales para cada entidad. Entre estos diagnósticos están los residuales de regresión, residuales estandarizados, valores predichos de la variable dependiente, intercepción, coeficientes de variable explicativa, errores estándar de coeficiente, estadísticas seudo t de coeficiente, significancia del coeficiente, influencia, D de Cook, R2 local y número de condición. Para más información sobre estos diagnósticos, consulte Cómo funciona Regresión ponderada geográficamente.

Gráficos

Se agregan los tres gráficos siguientes al panel Contenido:

• Relación entre variables: una matriz de gráficos de dispersión, con 1 variable dependiente y hasta 9 variables explicativas, que muestra la correlación entre la variable dependiente y cada variable explicativa y la correlación entre cada par de variables explicativas. Las correlaciones fuertes entre cualquier par indican multicolinealidad.
• Distribución del residual estandarizado: un histograma de los residuales estandarizados. Los residuales estandarizados se deben distribuir normalmente con un valor medio de cero y una desviación estándar de uno.
• Residuales estandarizados frente a predichos: un gráfico de dispersión entre los residuales estandarizados y sus valores predichos correspondientes. El diagrama debe ser aleatorio y no presentar patrones ni tendencias.

Salidas opcionales

Las siguientes salidas opcionales se pueden especificar en las listas desplegables Opciones de predicción y Opciones adicionales.

• El valor del parámetro Entidades predichas de salida es una clase de entidad con predicciones para la variable dependiente en las ubicaciones especificadas por el parámetro Ubicaciones de predicción.
• El valor del parámetro Tabla de vecindad de salida guarda una tabla que contiene los valores de las secciones Resumen de estadísticas para estimaciones de coeficientes y Resumen de variables explicativas y vecindades de los mensajes.
• El parámetro Espacio de trabajo de ráster de coeficiente especifica un espacio de trabajo (directorio o geodatabase) en el que se guardan los rásteres de los coeficientes. Estas superficies de ráster de coeficiente pueden ayudar a explicar la variación espacial presente en los coeficientes.

Multicolinealidad

La multicolinealidad se produce cuando dos o más variables explicativas están altamente correlacionadas en un modelo de regresión. Puede darse en los modelos OLS, GLR, GWR y MGWR. La multicolinealidad puede perjudicar a la estimación de coeficientes y vecindades óptimas ya que, si las variables explicativas están correlacionadas, comparten información mutua y el modelo de regresión no es capaz de distinguir entre los efectos de las variables. En casos moderados, las estimaciones de coeficiente estimadas pueden estar sesgadas y presentar una alta incertidumbre. En casos extremos, es posible que el modelo no se calcule. El siguiente ejemplo muestra una matriz de gráficos de dispersión de tres variables que están altamente correlacionadas entre sí y cualquier modelo de regresión que las utilice como variables explicativas podría presentar problemas con la multicolinealidad.

Cada par de variables está fuertemente correlacionada.

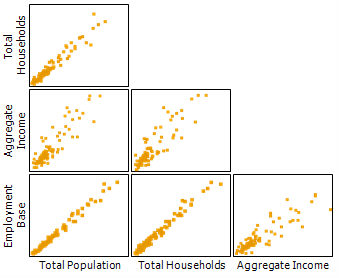
Identificación y prevención de la multicolinealidad en la MGWR

En un modelo MGWR, la multicolinealidad puede ocurrir en distintas situaciones:

• Una de las variables explicativas está muy agrupada espacialmente en clústeres. A medida que la MGWR se ajusta a los modelos de regresión local, cuando una entidad y todos sus vecinos tienen aproximadamente el mismo valor para una variable explicativa, es probable que se produzca la multicolinealidad.

  Para evitarlo, asigne cada variable explicativa e identifique las variables que presenten pocos valores posibles o en las que haya variables idénticas agrupadas espacialmente en clústeres. Si observa estos tipos de variables, considere la posibilidad de eliminarlas del modelo o representarlas de forma que aumente el rango de valores. Por ejemplo, un número variable de dormitorios se puede representar mejor como dormitorios por pie cuadrado.

• Dos o más variables explicativas altamente correlacionadas globalmente.

  Ejecute un modelo global con Regresión lineal generalizada y examine el Factor de inflación de la varianza (VIF) de cada variable explicativa. Si los valores VIF son grandes, por ejemplo, de 7,5 o más, la multicolinealidad global podría impedir que se ejecutara la MGWR. En este caso, las variables son redundantes; por lo tanto, considere la posibilidad de eliminar una de estas variables del modelo o combinarlas con otras variables explicativas para aumentar la variación en los valores.

• La vecindad definida es demasiado pequeña.

  La multicolinealidad también puede involucrar varias variables explicativas al mismo tiempo, lo que ocurre cuando las combinaciones lineales de algunas variables explicativas están altamente correlacionadas con combinaciones lineales de otras variables explicativas. Es más común en vecindades con una pequeña cantidad de vecinos. Para comprobarlo, verifique el número de condición local de la clase de entidad de salida. Un número de condición local alto indica que los resultados son inestables debido a la multicolinealidad local. Si este es el caso, vuelva a ejecutar el modelo utilizando una mayor cantidad de vecinos o bandas de distancia. Como regla, conviene ser escépticos ante los resultados en los que las entidades presenten un número de condición mayor que 30 o nulo. En el caso de los shapefiles, los valores nulos se representan con el valor -1,7976931348623158e+308. El número de condición es el ajuste de escala para corregir el número de variables explicativas del modelo, lo que permite comparar directamente el número de condición entre los modelos que utilizan un número diferente de variables explicativas.

La verificación de todas estas condiciones puede ayudar con los problemas de multicolinealidad, pero no siempre los resuelve.

Estimación de coeficiente y ancho de banda

Para todos los métodos de selección de vecindad excepto Búsqueda en gradiente, los coeficientes y anchos de banda de las variables explicativas se estiman a través de un proceso denominado ajuste de fondo (Breiman y otros, 1985). Desarrollado originalmente para estimar los parámetros de los modelos aditivos generalizados, este procedimiento recorre las variables explicativas una a una y utiliza una función de suavizado para calibrar el coeficiente mientras mantiene constantes el resto de variables explicativas. Este proceso se repite con las variables explicativas hasta que los valores de los coeficientes se estabilizan y no varían con cada sucesiva iteración.

Cuando se aplica a la MGWR (Fotheringham y otros, 2017), la función de suavizado es un modelo GWR univariante que resume la predicción ajustada por el residual anterior contra la variable explicativa simple (tratando al resto de variables explicativas como constantes). Este modelo GWR utiliza el mismo método de selección de vecindad (Búsqueda dorada, intervalos manuales o definido por el usuario) para estimar la escala espacial de la variable explicativa. Consulte la sección Recursos adicionales para obtener una descripción completa del proceso.

El algoritmo de ajuste de fondo debe comenzar con los valores inicializados de los coeficientes. Estos valores iniciales se calculan por medio de un modelo GWR de todas las variables explicativas. Si este modelo falla debido a la multicolinealidad, se utiliza la OLS en su lugar. Si el proceso no converge después de 25 iteraciones, se utilizan los valores de coeficiente de la iteración final.

Búsqueda en gradiente

La opción del método de selección de vecindad Búsqueda en gradiente es un enfoque más reciente para estimar los anchos de banda óptimos en la MGWR que no utiliza ajuste de fondo. Las principales ventajas de Búsqueda en gradiente son los tiempos de ejecución mejorados y el uso eficiente de la memoria. Este método es un algoritmo de optimización de segundo orden que utiliza el gradiente y la matriz hessiana para minimizar el AICc con respecto a la escala espacial de las variables explicativas. En lugar de actualizar el parámetro de una sola variable explicativa en cada paso iterativo, los parámetros de todas las variables explicativas se actualizan simultáneamente al descender en la dirección más empinada del gradiente, corregida por la curvatura del AICc.

Los resultados generados por Búsqueda dorada y Búsqueda en gradiente suelen ser muy similares. La siguiente imagen muestra la superficie de coeficiente verdadera junto con la superficie de coeficiente estimada de Búsqueda dorada y Búsqueda en gradiente. Observe que todas las superficies son similares y calculan la superficie verdadera con precisión.

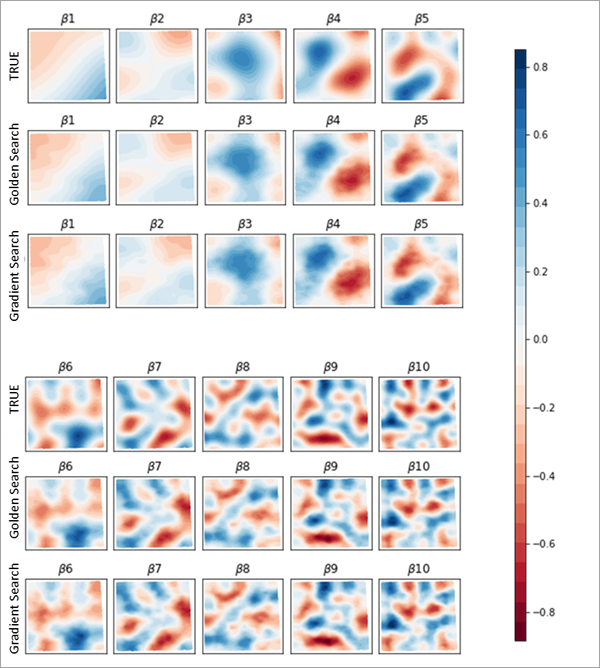
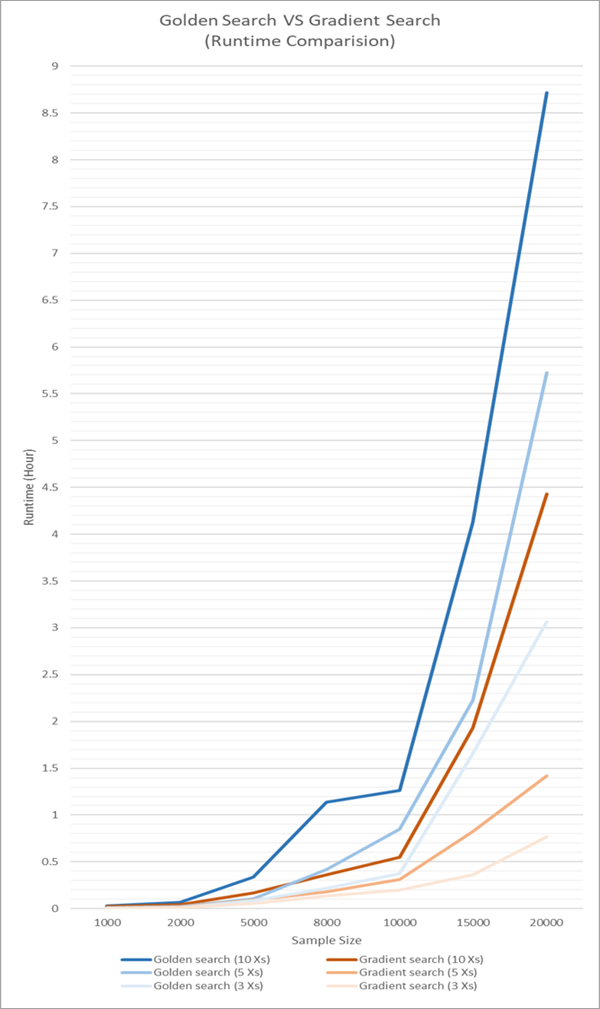
La siguiente imagen compara los tiempos de ejecución de Búsqueda dorada y Búsqueda en gradiente para distintos números de variables explicativas y distintos tamaños de dataset. Observe que el tiempo de ejecución de Búsqueda en gradiente es sistemáticamente más o menos la mitad del tiempo de ejecución de Búsqueda dorada para el mismo número de variables explicativas.

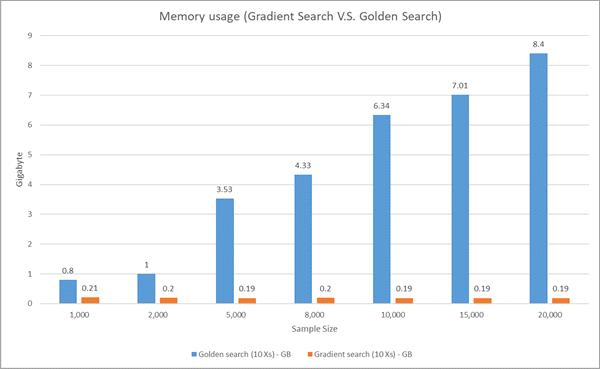
La siguiente imagen compara el uso de memoria de Búsqueda dorada y Búsqueda en gradiente. El uso de memoria de Búsqueda dorada aumenta rápidamente (crecimiento cuadrático) a medida que aumenta el tamaño de la muestra, pero el uso de memoria de Búsqueda en gradiente no se ve afectado por el tamaño de la muestra.

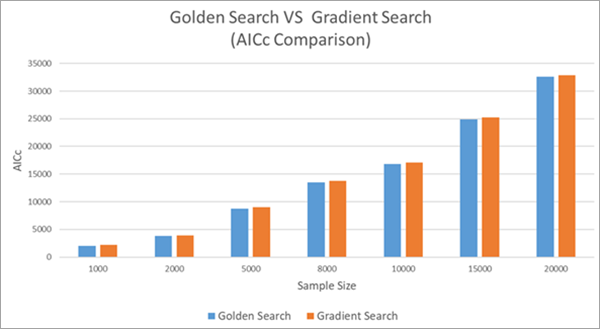
La siguiente imagen compara los valores de AICc de Búsqueda dorada y Búsqueda en gradiente. La precisión de los métodos es muy similar, pero Búsqueda dorada obtiene valores de AICc ligeramente más bajos (lo que indica una estimación algo más precisa) que Búsqueda en gradiente.

Recursos adicionales

Para obtener más información, consulte los recursos siguientes:

• Breiman, L., y J. H. Friedman. 1985. "Estimating optimal transformations for multiple regression and correlations (with discussion)". Journal of the American Statistical Association 80, (391): 580–619. https://doi.org/10.2307/2288473. JSTOR 2288473.
• Brunsdon C., A. S. Fotheringham y M. E. Charlton. 1996. "Geographically weighted regression: A method for exploring spatial nonstationarity". Geographical Analysis 28: 281–298.
• Conn, A.R., N.I.M. Gould y P.L. Toint. 2000. "Trust Region Methods." Society for Industrial and Applied Mathematics. https://doi.org/10.1137/1.9780898719857.
• da Silva, A. R. y A. S. Fotheringham. 2016. "The multiple testing issue in geographically weighted regression." Geographical Analysis 48(3), 233–247. https://doi.org/10.1111/gean.12084.
• Fotheringham, A. S., W. Yang y W. Kang. 2017. "Multiscale geographically weighted regression (MGWR)". Annals of the American Association of Geographers 107: 1247–265. https://doi.org/10.1080/24694452.2017.1352480
• Oshan, T. M., Z. Li, W. Kang, L. J. Wolf y A. S. Fotheringham. 2019. "mgwr: A Python implementation of multiscale geographically weighted regression for investigating process spatial heterogeneity and scale". ISPRS International Journal of Geo-Information 8: 269.
• Yu, H., A. S. Fotheringham, Z. Li, T. Oshan, W. Kang y L. J. Wolf. 2020. "Inference in multiscale geographically weighted regression". Geographical Analysis 52: 87–106.
• Zhou, X., R. Assunção, H. Shao, M. Janikas, C. Huang y H. Asefaw. 2023. "Gradient-based optimization for Multi-scale Geographically Weighted Regression." (en revisión)