| Label | Explanation | Data Type |
Input Features
| The input features containing the fields that will be used to select the SWM. | Feature Layer |
Input Fields
| The input fields that will be used to select the SWM. | Field |
Output Spatial Weights Matrix
| The output .swm file of the neighbors and weights selected by the tool. | File |
Unique ID Field | The unique ID field of the output .swm file. The field must be an integer and must have a unique value for each input feature. | Field |
Summary
Selects the spatial weights matrix (SWM) from a set of candidate SWMs that best represents the spatial patterns (such as trends or clusters) of one or more numeric fields.
The output spatial weights matrix file can then be used in tools that allow .swm files for their Neighborhood Type or Conceptualization of Spatial Relationships parameter values, such as the Bivariate Spatial Association (Lee's L), Hot Spot Analysis (Getis-Ord Gi*), and Cluster and Outlier Analysis (Anselin Local Moran's I) tools.
The tool selects the SWM by creating spatial components (called Moran eigenvectors) from each candidate SWM and testing how effectively the components represent the spatial patterns of the input fields.
Illustration
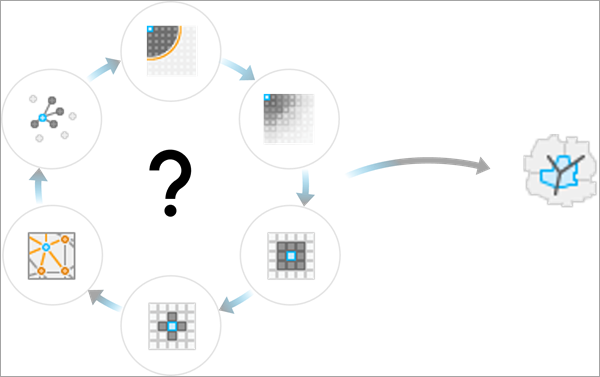
Usage
-
The purpose of the tool is to suggest a neighborhood type and weighting scheme (sometimes called a conceptualization of spatial relationships) that best represent the spatial patterns of the input fields by testing which spatial weighting produces spatial components that can most accurately predict the values of the input fields. The reasoning is that each spatial component has a spatial pattern, and the components that can most accurately predict the input fields are those that have the most similar patterns to the input fields. However, this suggested SWM is not intended to be a replacement for individual or expert knowledge of the data and its processes. There are many considerations to make when choosing a SWM for an analysis, and this tool only uses the ability of the spatial components to predict the input fields to determine the suggested SWM. In some cases, such as with the Hot Spot Analysis (Getis-Ord Gi*) tool, there are alternative methodologies for choosing a SWM, such as using the distance band that maximizes the spatial autocorrelation of the data (this is how the Optimized Hot Spot Analysis tool determines its neighbors and weights). It is recommended that you try alternative methodologies for neighborhoods and spatial weights and use the method that best aligns with the goals of the analysis.
Provide all the fields to the Input Fields parameter that you will use in any subsequent analysis using the output .swm file. For example, the Hot Spot Analysis (Getis-Ord Gi*) tool only requires one field, but the Bivariate Spatial Association (Lee's L) tool requires two fields. You can provide the output .swm file in the Weights Matrix File parameter after specifying the Get spatial weights from file option for the Neighborhood Type or Conceptualization of Spatial Relationships parameter of subsequent analysis tools.
The following SWMs will be tested by the tool:
- Five distance bands, each with unweighted, Gaussian, and bisquare kernels (15 total). The shortest distance band is the distance that results in at least one neighbor for each feature. The longest distance band is 20 percent of the diagonal extent of the input features. The other three distance bands are created by evenly incrementing between the shortest and longest distance bands. For polygon features, the distance between centroids is used to determine distances and neighbors.
- Four different numbers of neighbors (8, 16, 32, and 64), each with unweighted, Gaussian, and bisquare kernels (12 total). The bandwidths will be adaptive and equal to the distance to the (K+1)th neighbor, for K neighbors. If there are fewer than K input features, larger numbers of neighbors will be skipped. For example, if there are 50 input features, the three SWMs using 64 nearest neighbors will be skipped. For polygon features, the distance between centroids is used to determine distances and neighbors.
- For point features, the final SWM is a Delaunay triangulation neighborhood. For polygon features, the final SWM is a contiguity (edges and corners) neighborhood.
See How Neighborhood Summary Statistics works and Modeling spatial relationships for more information about each neighborhood and kernel weighting.
The geoprocessing messages include the Neighborhood Search History table that displays details of each tested SWM (such as the number of neighbors and weighting scheme) and the adjusted R-squared value of the SWM when used to predict the input fields. The SWM suggested by the tool will be the one with the largest adjusted R-squared and will be bolded and include an asterisk in the table.
The tool determines the suggested SWM using the following procedure:
- For each SWM, the Moran eigenvectors with the largest eigenvalues (those with strongest autocorrelation) are generated. The number of eigenvectors is equal to 25 percent of the number of features, up to a maximum of 100.
- Any eigenvectors that have negative Moran's I values (meaning that they are negatively autocorrelated) are filtered out.
- Each input field is predicted individually using the eigenvectors as explanatory variables in an ordinary least-squares regression model.
- The total sum of squares and residual sum of squares for all fields are aggregated, and a combined adjusted R-squared value is calculated.
- The SWM with the highest adjusted R-squared value is returned.
This procedure is fully described in the following reference:
Bauman, David, Thomas Drouet, Marie-Josée Fortin, and Stéphane Dray. 2018. "Optimizing the choice of a spatial weighting matrix in eigenvector-based methods." Ecology 99, no. 10: 2159-2166. https://doi.org/10.1002/ecy.2469.
Parameters
arcpy.stats.CompareNeighborhoodConceptualizations(in_features, input_fields, out_swm, id_field)
| Name | Explanation | Data Type |
in_features | The input features containing the fields that will be used to select the SWM. | Feature Layer |
input_fields [input_fields,...] | The input fields that will be used to select the SWM. | Field |
out_swm | The output .swm file of the neighbors and weights selected by the tool. | File |
id_field | The unique ID field of the output .swm file. The field must be an integer and must have a unique value for each input feature. | Field |
Code sample
The following Python window script demonstrates how to use the CompareNeighborhoodConceptualizations function:
# Select the spatial weights matrix (SWM) that best describes the
# spatial patterns of POP_SQMI.
arcpy.env.workspace = r"c:\data\project_data.gdb"
arcpy.stats.CompareNeighborhoodConceptualizations(
in_features="states",
input_fields="POP_SQMI",
out_swm=r"c:\data\states.swm",
id_field="unique_id_field"
)The following stand-alone script demonstrates how to use the CompareNeighborhoodConceptualizations function:
# Select the spatial weights matrix (SWM) that best describes
# the spatial patterns of two analysis field.
import arcpy
# Set the current workspace.
arcpy.env.workspace = r"c:\data\project_data.gdb"
# Run the tool.
arcpy.stats.CompareNeighborhoodConceptualizations(
in_features="myFeatureClass",
input_fields="myAnalysisField1;myAnalysis Field2",
out_swm=r"myOutputSWM.swm",
id_field="myUniqueIDField"
)
# Print the tool messages.
print(arcpy.GetMessages())