While you can get a sense of the orientation by drawing the features on a map, calculating the standard deviational ellipse makes the trend clear. You can calculate the standard deviational ellipse using either the locations of the features or the locations influenced by an attribute value associated with the features. The latter is termed a weighted standard deviational ellipse.
Calculations
The Standard Deviational Ellipse is given as:
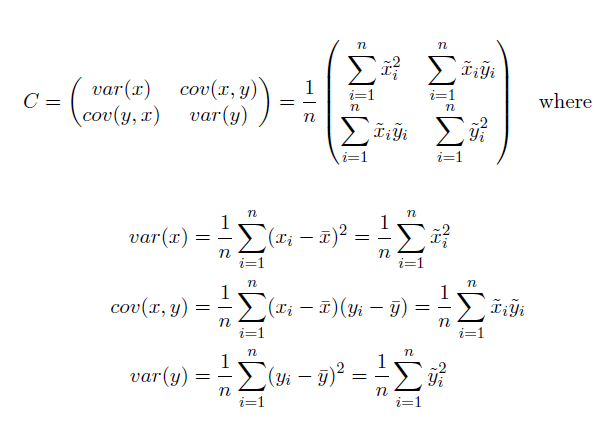
Where x and y are the coordinates for feature i, {x̄, ȳ} represent the Mean Center for the features and n is equal to the total number of features.
The sample covariate matrix is factored into a standard form which results in the matrix being represented by its eigenvalues and eigenvectors. The standard deviations for the x- and y-axis are then:
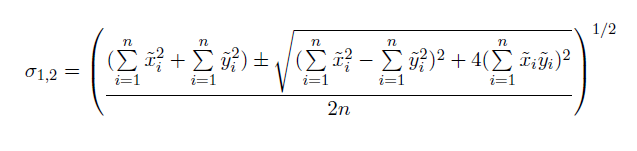
Visit the Additional resources if you would like to learn more about eigenvalues and eigenvectors.
Output and interpretation
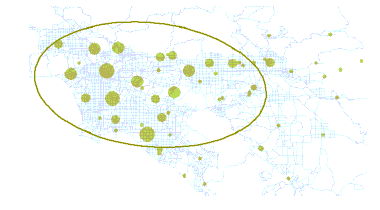
For two dimensional data, the Directional Distribution (Standard Deviational Ellipse) tool creates a new feature class containing an elliptical polygon centered on the mean center for all features (or for all cases when a value is specified for Case Field). The attribute values for these output ellipse polygons include two standard distances (long and short axes); the orientation of the ellipse; and the case field, if specified. The orientation represents the rotation of the long axis measured clockwise from noon. You can also specify the number of standard deviations to represent (1, 2, or 3).
Potential applications
- Mapping the distributional trend for a set of crimes might identify a relationship to particular physical features (a string of bars or restaurants, a particular boulevard, and so on).
- Mapping groundwater well samples for a particular contaminant might indicate how the toxin is spreading and, consequently, may be useful in deploying mitigation strategies.
- Comparing the size, shape, and overlap of ellipses for various racial or ethnic groups may provide insights regarding racial or ethnic segregation.
- Plotting ellipses for a disease outbreak over time may be used to model its spread.
- Examining the distribution of elevations for storms of a certain category would be a useful factor to consider when investigating the relationship between atmospheric conditions and aircraft accidents.
Additional resources
Chew, Victor. "Confidence, prediction, and tolerance regions for the multivariate normal distribution." Journal of the American Statistical Association 61.315 (1966): 605-617.
Fisher, N. I., T. Lewis, and B. J. J. Embleton. Statistical Analysis of Spherical Data. 1st ed. Cambridge: Cambridge University Press, 1987. Cambridge Books Online. Web. 26 April 2016.
Levine, Ned. "CrimeStat III: a spatial statistics program for the analysis of crime incident locations (version 3.0)." Houston (TX): Ned Levine & Associates/Washington, DC: National Institute of Justice (2004).
Mitchell, Andy. The ESRI Guide to GIS Analysis, Volume 2. ESRI Press, 2005.
Wang, Bin, Wenzhong Shi, and Zelang Miao. (2015) Confidence Analysis of Standard Deviational Ellipse and Its Extension into Higher Dimensional Euclidean Space. PLoS ONE 10(3), e0118537.