The Fuzzy Membership tool reclassifies or transforms the input data to a 0 to 1 scale based on the possibility of being a member of a specified set. 0 is assigned to those locations that are definitely not a member of the specified set, 1 is assigned to those values that are definitely a member of the specified set, and the entire range of possibilities between 0 and 1 are assigned to some level of possible membership (the larger the number, the greater the possibility).
The input values can be transformed by any number of functions and operators available in the ArcGIS Spatial Analyst extension that can reclassify the values to the 0 to 1 possibility scale. However, the Fuzzy Membership tool allows you to transform continuous input data based on a series of specific functions that are common to the fuzzification process. For example, the fuzzy Linear membership function transforms the input values linearly on the 0 to 1 scale, with 0 being assigned to the lowest input value and 1 to the largest input value. All the in-between values receive some membership value based on a linear scale, with the larger input values being assigned a greater possibility, or closer to 1.
In scripting, each of these functions is implemented as Python class.
Since these membership functions are specific to continuous input data, when you want to use categorical data for input to your Fuzzy Overlay analysis, you need to transform the data to the 0 to 1 possibility of membership scale using any number of Spatial Analyst tools. The two tools that are most useful for this process are Reclassify and Divide. The Reclassify tool allows you to transform your categorical data to a 0 to 10 scale (you cannot reclassify the data directly to the 0 to 1 scale with the tool), then divide the resulting transformed data by 10 to obtain the 0 to 1 scale.
Each membership function varies in its equation and application. Which function to use is based on which best captures the transformation of the data based on the phenomenon being modeled. You can further refine the characteristics of each membership function through a series of input parameters.
Below is a list of the different fuzzy membership functions and what they are best used for. A graph accompanies each function. On the x-axis are the input values (referred to as crisp values in the graphs) and on the y-axis are the transformed fuzzy membership values.
Fuzzy membership types
Following is a discussion of each of the seven fuzzy membership functions.
Fuzzy Gaussian
The Fuzzy Gaussian function transforms the original values into a normal distribution. The midpoint of the normal distribution defines the ideal definition for the set, assigned a 1, with the remaining input values decreasing in membership as they move away from the midpoint in both the positive and negative directions. The input values decrease in membership from the midpoint until they reach a point where the values move too far from the ideal definition and are definitely not in the set and are therefore assigned zeros.
Changes to the spread parameter alters the width and character of the transition zone.
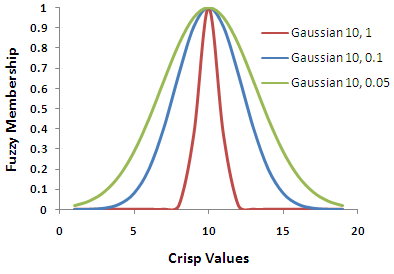
The Gaussian function is useful if the membership is near a specific value. For example, in a housing suitability model, for solar gain, south (180 degrees) may be the ideal aspect to build on, with aspects less than or greater than 180 being less favorable or less likely to belong to the ideal suitability set.
Fuzzy Large
The Fuzzy Large transformation function is used when the larger input values are more likely to be a member of the set. The defined midpoint identifies the crossover point (assigned a membership of 0.5) with values greater than the midpoint having a higher possibility of being a member of the set and values below the midpoint having a decreasing membership. The spread parameter defines the shape and character of the transition zone.
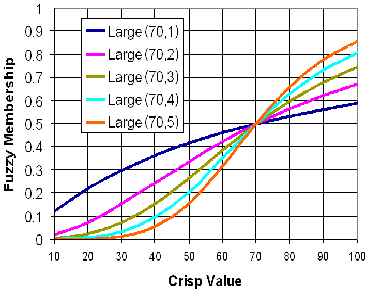
In the housing suitability model, the Fuzzy Large function can be used to transform the values of the distance from a landfill layer. The farther the locations are from the landfill, the more likely they are to be a member of the favorable suitability set.
Fuzzy Linear
The Fuzzy Linear transformation function applies a linear function between the user-specified minimum and maximum values. Anything below the minimum will be assigned a 0 (definitely not a member) and anything above the maximum a 1 (definitely a member). The blue line in the image below represents a positive sloped linear transformation with a minimum of 30 and a maximum of 80. Any value below 30 will be assigned a zero and anything above 80 a 1.
If the minimum is greater than the maximum, a negative linear relationship (a negative slope) is established. The red line in the image below represents a negative slope linear transformation. Any value less than 30 will be assigned a 1 and anything above 80 a 0.
Where the slope of the line is increasing or decreasing defines the transition zone (between 30 to 80 in the image below).
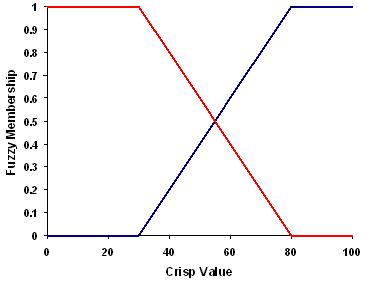
The Fuzzy Linear transformation function in the housing suitability example can be used for the distance from recreational areas criteria (a negative linear transformation). Any location that is within 500 meters of a recreation area could be definitely in the favorable suitable set, while 500 to 10,000 meters linearly decreases in possibility of being in the suitable set, and any location farther than 10,000 meters would be too far from a recreational area to be part of the favorable set and would be assigned a 0.
Fuzzy MS Large
The Fuzzy MS Large transformation function is similar to the Fuzzy Large function, except the definition of the function is based on a specified mean and standard deviation. Generally, the difference between the two functions is that the Fuzzy MS Large function can be more applicable if the very large values are more likely to be a member of the set.

The result can be similar to the Large function depending on defined mean and standard deviation.
Fuzzy MS Small
The Fuzzy MS Small transformation function is similar to the Fuzzy Small function, except the definition of the function is based on a specified mean and standard deviation. Generally, the difference between the two functions is that the Fuzzy MS Small function can be more applicable if the very small values are more likely to be a member of the set.
The result can be similar to the Small function depending on how the multipliers of the mean and standard deviation are defined.
Fuzzy Near
The Fuzzy Near transformation function is most useful if membership is near a specific value. The function is defined by a midpoint defining the center of the set, identifying definite membership and therefore assigned a 1. As values move from the midpoint, in both the positive and negative directions, membership decreases until it reaches 0, defining no membership. The spread defines the width and character of the transition zone.
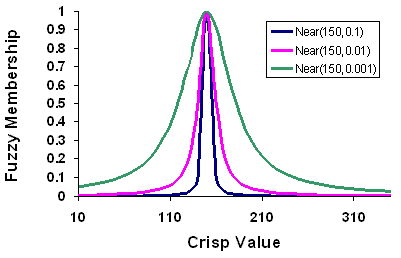
Fuzzy Near and Fuzzy Gaussian can be similar, depending on the specified parameters. The Fuzzy Near function generally decreases at a faster rate, with a more narrow spread, than Fuzzy Gaussian function and is therefore used when the values very near the midpoint are more likely to be a member of the set.
Fuzzy Small
The Fuzzy Small transformation function is used when the smaller input values are more likely to be a member of the set. The defined midpoint identifies the crossover point (assigned a membership of 0.5) with values greater than the midpoint having a lower possibility of being a member of the set and values below the midpoint having a higher possibility of membership. The spread parameter defines the shape and character of the transition zone.
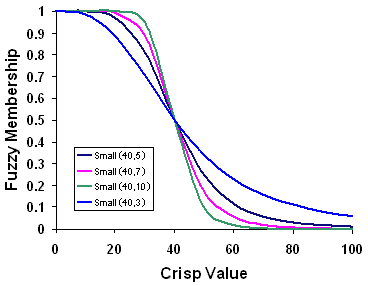
The Fuzzy Small transformation function in the housing suitability example can be used for the distance from power criteria. As the distance from a power line increases, it is more expensive to access power, so it is less likely that the locations will be members of the favorable suitable set. The access to power criteria is not modeled as a linear transformation to account for the need for electrical transformers as the distance increases.