Funktionsweise von "Auf Vorhandensein beschränkte Vorhersage (MaxEnt)"

Das Werkzeug Auf Vorhandensein beschränkte Vorhersage (MaxEnt) schätzt anhand der maximalen Entropie (MaxEnt) die Wahrscheinlichkeit für das Vorhandensein eines Phänomens. Das Werkzeug stellt anhand bekannter Punkte des Vorkommens und erklärender Variablen in Form von Feldern, Rastern oder Entfernungs-Features eine Schätzung des Vorhandenseins in einem Untersuchungsgebiet bereit. Sie können mit dem trainierten Modell das Vorhandensein in unterschiedlichen Daten vorhersagen, wenn entsprechende erklärende Variablen bekannt sind. Im Gegensatz zu anderen Methoden, die definierte Positionen des Fehlens voraussetzen oder explizit erfordern, kann Auf Vorhandensein beschränkte Vorhersage auf Vorhersageprobleme angewendet werden, wenn nur das Vorhandensein des Ereignisses bekannt ist.

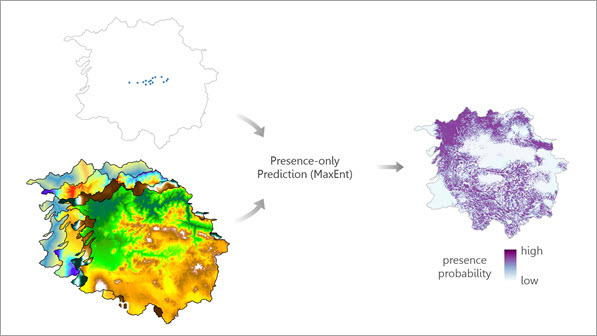
Potenzielle Anwendungsbereiche

Anwendungsbeispiele betreffen in der Regel die Modellierung des Vorhandensein von Arten für Zwecke des Umwelt- und Naturschutzes, jedoch umfassen Anwendungen der Vorhersage des Vorhandenseins vielfältige Bereiche und Anwendungen:

• Eine Ökologin hat Felddaten zu beobachteten Positionen des Vorhandenseins einer Pflanzenart gesammelt. Sie muss das Vorhandensein der Art in einem größeren Untersuchungsgebiet schätzen. Die Ökologin kann anhand der bekannten Positionen des Vorhandenseins und mithilfe zugrunde liegender Faktoren als Raster das Vorhandensein der Art modellieren und eine Karte vorhergesagter Positionen erstellen, an denen die Art mit der größten Wahrscheinlichkeit vorhanden ist.
• Ein Forscher möchte die Auswirkungen des Klimawandels auf den Lebensraum einer sensiblen Art ermitteln. Er modelliert das Vorhandensein anhand bekannter Positionen des Vorhandenseins und einer Reihe erklärender Variablen, einschließlich klimabezogener Faktoren wie Temperatur und Niederschlägen. Der Forscher modelliert mithilfe projizierter Klimawandel-Raster-Oberflächen eine geschätzte Verteilung der Arten gemäß den in den erklärenden Variablen festgestellten Auswirkungen des Klimawandels. Dies ergibt eine Schätzung des neuen Lebensraumes der Arten entsprechend den projizierten Auswirkungen des Klimawandels.
• Ein Analyst für Hochwassergefahren möchte die Wahrscheinlichkeit von Überschwemmungen nach dem Eintreffen eines Hurrikans in einem Untersuchungsgebiet schätzen. Als Ergänzung zum Einsatz hochauflösender Luftbilder während des Ereignisses verwendet er räumlich verteilte physische und sozioökonomische Merkmale in Kombination mit Crowdsourcing-Daten, um das Vorhandensein von Überschwemmungen zu modellieren. Mithilfe dieses Modells identifiziert der Analyst, wo die Wahrscheinlichkeit am größten ist, dass Menschen nach dem Hurrikan unmittelbare Nothilfe benötigen (Mobley et. al, 2019).
• Ein Epidemiologe modelliert das Auftreten neuer Infektionskrankheiten. Er verwendet vorhandene bekannte Orte, an denen Erreger übergesprungen sind, und ökologische Faktoren wie Temperatur, Niederschlag, Landbedeckung, den normalisierten differenzierten Vegetationsindex (NDVI) sowie die Sonnenscheindauer als Einflussvariablen in einem Modell. Mithilfe des Modells wird eine vorläufige Risikoprognose erstellt, aus der die Eignung für das Auftreten neuer Infektionskrankheiten hervorgeht (Du et. al., 2014).

MaxEnt

Eine Facette der räumlichen Analyse betrifft das Modellieren und Schätzen des geographischen Vorkommens eines Ereignisses. Anwendungsbeispiele betreffen in der Regel die Modellierung des Vorhandenseins von Arten für Zwecke des Umwelt- und Naturschutzes, jedoch umfassen Anwendungen der Vorhersage des Vorhandenseins vielfältige Bereiche und Anwendungen.

In manchen Fällen werden Daten zum Vorhandensein als Anzahl von Ereignissen des Vorhandenseins in quadratischen Zellen aufgezeichnet: Durch jede Beobachtung wird eine Anzahl an der Position erhöht. Zum Modellieren dieser Anzahl können verschiedene Modellierungsmethoden verwendet werden, z. B. die Poisson-Methode des Werkzeugs Generalisierte lineare Regression. In anderen Fällen werden explizite Daten zu Vorhandensein und Fehlen in bestimmten Intervallen an bekannten Positionen aufgezeichnet, z. B. in Stationen zur Überwachung der Luftqualität, die gesundheitsschädliche Ozonwerte aufzeichnen. In diesen Fällen handelt es sich bei der Modellierung von Vorhandensein und Fehlen um eine binäre Klassifizierung, für die verschiedene Methoden, z. B. die logistische Regression, genutzt werden können.

Bei der Modellierung des Vorhandensein von Arten durch Ökologen und in verschiedenen anderen Bereichen, bei denen häufig das Vorhandensein eines Ereignisses, jedoch selten das Fehlen aufgezeichnet wird, erschwert der Mangel an expliziten Daten zum Fehlen das Modellieren von Vorhandensein und Fehlen mithilfe von Mehrklassen-Vorhersagemethoden.

Für MaxEnt werden Daten zum Fehlen weder vorausgesetzt noch benötigt. MaxEnt ist eine universelle Methode für Vorhersagen oder Inferenzen aus unvollständigen Informationen (Phillips et al. 2006). MaxEnt vergleicht anhand eines Satzes bekannter Positionen des Vorhandensein und anhand erklärender Variablen, die das Untersuchungsgebiet beschreiben, die Bedingungen an den Positionen des Vorhandensein mit dem Untersuchungsgebiet, um eine Wahrscheinlichkeitsoberfläche für das Vorhandensein zu schätzen.

MaxEnt basiert im Wesentlichen auf drei primären Eingaben:

• Der Position bekannter Punkte des Vorhandenseins.
• Einem Untersuchungsgebiet.
• Erklärenden Variablen (Kovariablen) zur Beschreibung der Umweltfaktoren, die im Zusammenhang mit dem Vorhandensein im Untersuchungsgebiet stehen können.

Das Untersuchungsgebiet definiert einen Bereich, in dem ein Vorhandensein möglich ist. Es wird häufig durch eine Reihe unbekannter Positionen des Vorhandenseins dargestellt. Diese Positionen werden auch als Hintergrundpunkte bezeichnet und von der MaxEnt-Methode verwendet, um die Bedingungen an Positionen des Vorhandenseins und im Untersuchungsgebiet gegenüberzustellen und so eine Wahrscheinlichkeitsoberfläche für das Vorhandensein zu schätzen.

Die Wahrscheinlichkeitsoberfläche für das Vorhandensein kann viele Formen aufweisen. Durch MaxEnt wird die Form gewählt, die der Umgebung am stärksten entspricht, aus der sie abgeleitet wurde, und reduziert alle anderen Annahmen (d. h., die Entropie wird maximiert). "It agrees with everything that is known, but carefully avoids assuming anything that is not known" (Alles, was bekannt ist, wird übernommen. Jedoch wird nichts übernommen, was unbekannt ist.). (Jaynes 1990).

MaxEnt umfasst zusätzlich zu seinem Modellierungsverfahren Schritte für die Vorbereitung der Eingabedaten, die Transformation erklärender Variablen, die Vorbereitung der Ausgabedaten und die Modellvalidierung. Dies macht sie zu einer robusten Methode für die Modellierung von auf Vorhandensein beschränkten Phänomenen.

Verwenden des Werkzeugs "Auf Vorhandensein beschränkte Vorhersage (MaxEnt)"

Das Werkzeug Auf Vorhandensein beschränkte Vorhersage umfasst Aspekte der Datenvorbereitungs-, Modellierungs-, Variablenauswahl- und Vorhersage-Workflows von MaxEnt. Dieser Abschnitt bietet wichtige Informationen über die einzelnen Parameter, um Ihnen das Erstellen besser geeigneter Modelle zu erleichtern.

Angeben von bekannten Positionen des Vorhandenseins und von Hintergrundpunkten

Die auf Vorhandensein beschränkte Vorhersage erfordert Eingabedaten, um bekannte Positionen des Vorhandenseins darzustellen. Mit dem Parameter Eingabe-Punkt-Features wird ein vorhandenes Dataset mit diesen Positionen angegeben.

Eingabe-Punkt-Features enthalten keine Hintergrundpunkte

Wenn die Eingabe-Punkt-Features keine Hintergrundpunkte enthalten, können Sie den Parameter Enthält Hintergrundpunkte deaktiviert lassen.

Wenn der Parameter Enthält Hintergrundpunkte deaktiviert ist, verwendet das Werkzeug die gröbsten Zellenschwerpunkte sich überschneidender Werte des Parameters Erklärende Trainings-Raster im Untersuchungsgebiet, um Hintergrundpunkte automatisch zu erstellen.

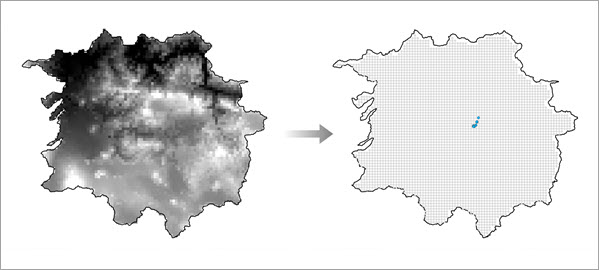
Sie können mit dem Parameter Trainierte Ausgabe-Features eine Ausgabe erstellen, die vom Werkzeug erstellte Hintergrundpunkte enthält.

Eingabe-Punkt-Features enthalten Hintergrundpunkte

Wenn die Eingabe-Punkt-Features Hintergrundpunkte enthalten, können Sie die Parameter Enthält Hintergrundpunkte und Vorhandensein-Indikatorfeld mit Feldwerten verwenden, die die jeweilige Position als Vorhandensein (1) oder Hintergrund (0) kennzeichnen.

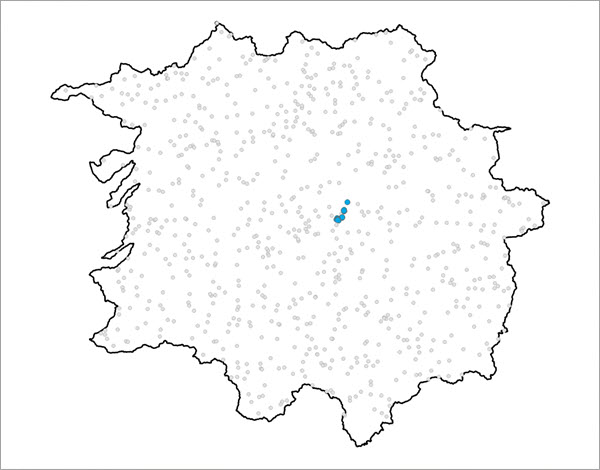
Das Verhältnis zwischen Hintergrundpunkten und Punkten des Vorhandenseins hat erhebliche Auswirkungen auf die Vorhersageergebnisse. Unabhängig davon, ob Hintergrundpunkte in den Eingabe-Punkt-Features bereitgestellt oder vom Werkzeug erstellt werden, wird empfohlen, die Klassifizierungsdiagnosen für die Modelle mit unterschiedlichen Mengen von Hintergrundpunkte zu überprüfen und zu vergleichen. Mit dem Parameter Räumliche Ausdünnung können Sie die Anzahl der Hintergrundpunkte in der Analyse verringern. Weitere Informationen finden Sie in den Abschnitten Definieren eines Untersuchungsgebiets und Reduzieren der Stichprobenverzerrung mithilfe von räumlicher Ausdünnung unten.

Hinweis:

Zum Erstellen eines Modells mit dem Werkzeug müssen die Trainingsdaten mindestens zwei Punkte des Vorhandenseins und zwei Hintergrundpunkte enthalten.

Angeben von erklärenden Variablen

Zum Erstellen des Vorhersagemodells verwendet das Werkzeug zusätzlich zu bekannten Punkten des Vorhandenseins und Hintergrundpunkten erklärende Variablen. Es gibt drei Methoden zum Angeben erklärender Variablen: mit Rastern, mit Feldern in den Eingabe-Punkt-Features und mit Entfernungs-Features. Für Raster und Felder können erklärende Variablen kontinuierlich oder kategorial sein. Für kategoriale erklärende Variablen erfordert das Werkzeug mindestens drei Datenpunkte pro Kategorie.

Verwenden erklärender Variablen aus Rastern

Sie können mit Rastern Bedingungen in der Landschaft darstellen, die möglicherweise hilfreiche Einflussvariablen für das Vorhandensein eines Ereignisses sind. Beispielsweise ist eine Pflanzenart eventuell stark von einem bestimmten Höhenbereich abhängig. Sie können dann mit einem Höhen-Raster den Positionen des Vorhandenseins der Pflanze im Modell Höhenwerte zuordnen.

Aktivieren Sie das Kontrollkästchen Kategorisch, wenn Raster Kategoriedaten, z. B. Landbedeckungsklassen, darstellen.

Wenn die Eingabe-Punkt-Features keine Hintergrundpunkte enthalten, ist die Verwendung erklärender Variablen erforderlich, da jede Zelle im Untersuchungsgebiet zum Erstellen eines Hintergrundpunktes verwendet wird.

Die Zellengrößen der Werte des Parameters Erklärende Trainings-Raster wirken sich erheblich auf die Verarbeitungszeit aus: je höher die Auflösung, desto länger die Verarbeitungszeit. Aus diesem Grund gilt für das Werkzeug eine Begrenzung auf insgesamt 100 Millionen Zellen im Interessenbereich. Sie können mit dem Werkzeug Resampling die räumliche Auflösung des Rasters verringern, sodass die Anzahl der Zellen und die Verarbeitungszeit verringert werden.

Verwenden erklärender Variablen aus Feldern

Geben Sie mit dem Parameter Erklärende Trainingsvariablen Felder an, deren Attribute beim Modellieren des Vorhandenseins des Phänomens als erklärende Variablen verwendet werden. Diese Option ist nur verfügbar, wenn Eingabe-Punkt-Features Hintergrundpunkte enthalten und der Parameter Enthält Hintergrundpunkte aktiviert ist.

Verwenden Sie das Kontrollkästchen Kategorisch, um anzugeben, ob ein im Parameter Erklärende Trainingsvariablen angegebenes Feld ein kategoriales Feld ist.

Verwenden erklärender Variablen aus Entfernungs-Features

Verwenden Sie den Parameter Erklärende Trainings-Entfernungs-Features, um Features anzugeben, deren Nähe zu den Eingabe-Punkt-Features als erklärende Variablen verwendet wird. Diese Option ist nur verfügbar, wenn Eingabe-Punkt-Features Hintergrundpunkte enthalten und der Parameter Enthält Hintergrundpunkte aktiviert ist.

Entfernungs-Features dienen zum automatischen Erstellen erklärender Variablen durch die Berechnung der Entfernung zwischen den Eingabe-Punkt-Features und dem nächsten bereitgestellten Feature. Wenn es sich bei dem Parameterwert Erklärende Trainings-Entfernungs-Features um Polygone oder Linien handelt, werden die Entfernungsattribute als Entfernung zwischen den nächstgelegenen Segmenten des Feature-Paares berechnet. Entfernungen werden für Polygone und Linien unterschiedlich berechnet. Weitere Informationen hierzu finden Sie unter So wird die Entfernung mit Nachbarschaftsanalyse-Werkzeugen berechnet.

Aus Gründen der Performance ist der Parameter Erklärende Trainings-Entfernungs-Features nicht verfügbar, wenn Eingabe-Punkt-Features keine Hintergrundpunkte enthalten. Sie können jedoch bei Verwendung von auf Vorhandensein beschränkten Punkten Entfernungs-Features verwenden, indem Sie mit dem Werkzeug Entfernungsakkumulation Entfernungs-Raster erstellen. Entfernungs-Raster enthalten Zellen mit Werten, die die Entfernung zwischen der Zelle und dem nächstgelegenen Feature in einer angegebenen Datenquelle beschreiben. Nach der Erstellung von Entfernungs-Rastern können Sie diese als Eingaben im Parameter Erklärende Trainings-Raster für auf Vorhandensein beschränkte Eingabe-Punkt-Features verwenden.

Vorbereiten der Daten für die Modelleingaben

Das Werkzeug umfasst Datenvorbereitungsschritte für die bereitgestellten Eingabe-Punkt-Features und erklärenden Variablen. Die Datenvorbereitung umfasst die Variablentransformation mittels Basisfunktionen, das Angeben eines Untersuchungsgebiets und das Verringern der Stichprobenverzerrung mithilfe von räumlicher Ausdünnung.

Transformieren erklärender Variablen mithilfe von Basisfunktionen

In MaxEnt werden die Eigenschaften der Landschaft als potenzielle erklärende Variablen verwendet. In einigen Fällen weisen die günstigen Bedingungen für Vorhandensein möglicherweise komplexe Beziehungen zum Vorkommen des Ereignisses auf. Um komplexere Beziehungsformen in das Modell zu integrieren, transformiert (oder erweitert) das Werkzeug die potenziellen erklärenden Variablen mithilfe von Basisfunktionen.

Sie können beim Ausführen des Werkzeugs mit dem Parameter Erweiterungen von erklärenden Variablen (Basisfunktionen) mehrere Basisfunktionen auswählen. Anschließend werden alle transformierten Versionen der erklärenden Variablen im Modell verwendet. Die Variablen mit der besten Performance werden durch Normalisierung ausgewählt. Bei dieser Methode der Variablenauswahl wird ein Kompromiss zwischen Eignung und Komplexität des Modells erzielt.

Es gibt fünf Typen von Basisfunktionen, bei denen jeweils unterschiedliche Überlegungen für die Modellierung komplexer Phänomene berücksichtigt werden.

• Original (Linear): Wendet eine lineare Basisfunktion auf die Eingabevariablen an und kann verwendet werden, wenn keine Transformation angewendet werden muss. Dies ist die Standardoption.

  In einem Beispielanwendungsfall wird das Werkzeug verwendet, um das Vorhandensein einer Art zu modellieren, von der bekannt ist, dass sie Zugang zu einem Wasserlauf benötigt. Die Verwendung der linearen Basisfunktion für eine Variable, die der Entfernung zu einem Wasserlauf entspricht, ermöglicht es dem Modell, die lineare Beziehung zwischen dem Vorhandensein einer Art und der Entfernung zu einem Wasserlauf zu schätzen. Der resultierende Koeffizient kann verwendet werden, um die marginale lineare Beziehung zu interpretieren, bevor komplexere Beziehungsformen betrachtet werden.

  Verwenden Sie die Basisfunktion Original (Linear), wenn die Auswertbarkeit im Modell einen hohen Stellenwert hat. Da keine Transformation erfolgt, ist das Auswerten der Koeffizienten bezüglich ihrer Auswirkung auf die Wahrscheinlichkeit des Vorhandenseins mit der Methode "Linear" am einfachsten.

  

  Hinweis:

  Kategoriale erklärende Variablen lassen nur die Verwendung der Basisfunktion Original (Linear) zu. Wenn sowohl kontinuierliche als auch kategoriale erklärende Variablen angewendet werden, können Sie mehrere Basisfunktionen auswählen. Auf die kategorialen Variablen wird jedoch nur die Basisfunktion Original (Linear) angewendet.

• Squared (Quadratic): Transformiert jeden Wert einer erklärenden Variable, indem er quadriert wird. Dies führt zu einer quadratischen Beziehung zwischen der erklärenden Variablen und der Antwort für das Vorhandensein. In einigen Bereichen, z. B. bei der Verteilung der Arten, sind die Reaktionen der Arten auf Umgebungsbedingungen häufig unimodal und nicht linear (Austin 2002, 2007). In solchen Fällen werden die Beziehungen möglicherweise durch eine quadratische Form am besten dargestellt.

  In manchen Fällen ist die Beziehung einer erklärenden Variable mit einem Reaktionsereignis zwangsläufig quadratisch, während die Stichprobendaten in den Eingabe-Punkt-Features möglicherweise nur eine Facette der parabolischen Beziehung darstellen. Beispielsweise kann eine tropische Art eine parabolische Beziehung zur Temperatur aufweisen: Äußerst niedrige Temperaturen führen zu einer geringen Wahrscheinlichkeit des Vorhandenseins, tropische Temperaturen führen zu einer hohen Wahrscheinlichkeit, und äußerst hohe Temperaturen führen wiederum zu einer geringen Wahrscheinlichkeit. Wenn äußerst niedrige Temperaturen in den Stichprobendaten für diese Art nicht enthalten sind, kann die Beziehung einfach durch eine lineare Beziehung dargestellt werden (Merow et al., 2013).

  

• Paarweise Interaktion (Product): Führt eine paarweise Multiplikation erklärender Variablen durch. Wenn z. B. drei Variablen A, B und C ausgewählt werden, erzeugt diese Basisfunktion transformierte Variablen, die den Ergebnissen von A x B, A x C und B x C entsprechen. Diese transformierten Variablen werden i. d. R. als Interaktionsterme bezeichnet. Sie sind möglicherweise hilfreiche Darstellungen komplexer Beziehungen, die von Bedingungen zwischen mehreren Variablen abhängen. Beispielsweise ist ein Interaktionsterm, der Einkommen und Entfernung umfasst, eventuell eine stärkere Einflussvariable für den Kundenkreis als die einzelnen Einflussvariablen für Einkommen und Entfernung.

  Erklärende Variablen, die mit der Methode Paarweise Interaktion (Product) transformiert wurden, können für die Modellierung der Interaktion zwischen Umgebungsbedingungen hilfreich sein. Die Auswertung des Modells ist jedoch möglicherweise komplizierter, da Interaktionsterme es schwierig machen, die Auswirkungen der einzelnen erklärenden Variablen miteinander zu vergleichen. Dies fällt besonders ins Gewicht, wenn die Plots der Koeffizienten und partiellen Antworten der einzelnen erklärenden Variablen ausgewertet werden.

  

  Hinweis:

  Die Option Paarweise Interaktion (Product) ist nur verfügbar, wenn mehrere kontinuierliche erklärende Variablen ausgewählt werden.

• Einzelschritt (Threshold): Konvertiert die kontinuierliche erklärende Variable durch das Anwenden einer schrittweisen Funktion in eine binäre erklärende Variable: Werten unter dem Schwellenwert wird der Wert 0 und Werten über dem Schwellenwert der Wert 1 zugewiesen.

  Der Parameter Anzahl von Knoten steuert die Anzahl der erstellten Schwellenwerte. Diese werden dann zum Erstellen mehrerer transformierter binärer erklärender Variablen unter Verwendung des jeweiligen Schwellenwertes verwendet. Die Schwellenwerte werden zwischen dem Minimal- und Maximalwert in der erklärenden Variable angewendet, um Segmente gleicher Länge zu erstellen.

  In einem Beispielanwendungsfall wird Auf Vorhandensein beschränkte Vorhersage ausgeführt, um die Auswirkungen hoher Temperaturen auf das Vorkommen zu untersuchen (Beispiel: über 32 Grad Celsius oder unter 32 Grad Celsius). Mit der Schwellenwert-Basisfunktion wird die kontinuierliche Temperaturvariable in die Werte 1 (über 32 Grad) und 0 (unter 32 Grad) unterteilt, sodass jede Bedingung in Bezug auf Vorhandensein ausgewertet werden kann.

  

• Geglätteter Schritt (Hinge): Konvertiert die kontinuierliche erklärende Variable in zwei Segmente: ein statisches Segment (alle Werte lauten 0 oder 1) und eine lineare Funktion (steigend oder abnehmend), die durch einen als Knoten bezeichneten Schwellenwert getrennt werden. Dies kann mit Forward Hinge (mit den 0 betragenden Werten zwischen dem Minimum und dem Knoten beginnen und dann zwischen dem Knoten und dem Maximum eine steigende lineare Funktion anwenden) oder Reverse Hinge (mit einer zunehmenden linearen Funktion zwischen dem Minimum und dem Knoten beginnen und dann zwischen dem Knoten und dem Maximum alle 1 betragenden Werte anwenden) erfolgen.

  Der Parameter Anzahl von Knoten steuert die Anzahl der erzeugten Transformationen erklärender Variablen, sodass (Anzahl von Knoten - 1) * 2 transformierte erklärende Variablen erzeugt werden. Diese Formel drückt aus, dass die Anzahl der Knoten der Anzahl der gleichen Intervalle zwischen dem Minimal- und Maximalwert in der erklärenden Variablen entspricht (Anzahl von Knoten minus 1) und sowohl mit Forward Hinge transformierte Variablen als auch mit Reverse Hinge transformierte Variablen erstellt werden (Multiplikation mit 2).

  In einem Beispielanwendungsfall wird das Werkzeug ausgeführt, um die Auswirkungen der Schwankungen hoher Temperaturen zu untersuchen (Beispiel: Beibehalten aller Werte über 32 Grad Celsius und Ignorieren aller niedrigeren Werte). Mit der Hinge-Basisfunktion kann die Schwankung der Variable über dem Knoten bleiben (indem eine lineare Funktion für alle Werte über 32 Grad angewendet wird) und für alle Daten unter dem Knoten das Rauschen reduziert werden (indem alle Werte unter 32 Grad in 0 umgewandelt werden).

  Die Optionen Geglätteter Schritt (Hinge) und Einzelschritt (Threshold) sind abschnittsweise definierte Funktionen, die sich gegenseitig ausschließen. Wenn eine ausgewählt ist, kann die andere nicht ausgewählt werden. Es wird empfohlen, bei Auswahl einer dieser Funktionen mehrere Ausführungen des Modells zu testen und den Wert des Parameters Anzahl von Knoten anzupassen, um zu ermitteln, wie das Modell durch die Schwellenwerte unterstützt oder beeinträchtigt wird.

  

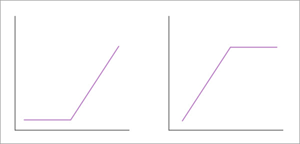
  Das Werkzeug verwendet beim Modellieren komplexer Bedingungen, die das Vorhandensein eines Phänomens begünstigen, mehrere transformierte Versionen der einzelnen erklärenden Variablen. Beispielsweise kann ein Modell, das die Wahrscheinlichkeit des Vorhandenseins einer Wüstenschildkrötenart anhand der jährlichen Durchschnittstemperatur schätzt, verschiedene Variablenerweiterungen verwenden, um eine komplexe Beziehung zwischen Temperatur und Lebensräumen von Wüstenschildkröten zu beschreiben.

  

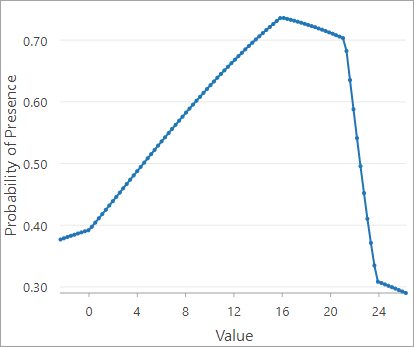
  Aus dem oben gezeigten Plot der partiellen Antworten geht die marginale Antwort der Wahrscheinlichkeit des Vorhandenseins bei Änderungen der jährlichen Durchschnittstemperatur hervor. Wenn alle anderen Faktoren gleich bleiben, ändert sich die Wahrscheinlichkeit des Vorhandenseins wie folgt:

  • Linearer Anstieg bei einem Anstieg der jährlichen Durchschnittstemperatur um 0 bis 15 °C
  • Allmählicher Rückgang bei 15 bis 21 °C
  • Schneller Rückgang bei jährlichen Durchschnittstemperaturen über 21 °C

  Das Werkzeug generiert mithilfe mehrerer Basisfunktionen erklärende Variablenerweiterungen, die diesen Beziehungstyp am besten darstellen. Dabei werden die hilfreichsten Transformationen durch einen Prozess ausgewählt, der als Vereinfachung bezeichnet wird.

Normalisierung

MaxEnt kann zu einer Überanpassung der Daten führen. Zum Verringern des Problems wendet die Methode eine Form der Normalisierung an, mit der große Koeffizienten erklärender Variablen sanktioniert werden. Dies erzwingt die Konzentration des Modells auf die wichtigsten erklärenden Variablen (Phillips et al. 2006).

Die Normalisierung lässt sich folgendermaßen darstellen: Für alle erklärenden Variablen gemeinsam, die vom Modell bereitgestellt werden, ist ein begrenztes Budget an Koeffizienten vorhanden. Wenn Koeffizienten verringert werden, um das Budget nicht zu überschreiten, werden mehrere erklärende Variablen mit niedrigen Koeffizienten auf Null reduziert und somit aus dem Modell entfernt. Dies bewirkt, dass das Modell weniger erklärende Variablen enthält, und zwar nur solche, deren Koeffizienten hoch genug sind, um auch unter einem begrenzten Budget an Koeffizienten im Modell zu verbleiben. Mit einer geringeren Anzahl erklärender Variablen verringert sich die Wahrscheinlichkeit einer Überanpassung des Modells, und es ist einfacher auszuwerten. Aus Gründen der Übersichtlichkeit ist die einfachste Erklärung eines Phänomens in der Regel die beste (Phillips et al., 2006).

Normalisierung erleichtert auch die Behandlung von Multikollinearität: Wenn miteinander in Beziehung stehende erklärende Variablen hinzugefügt werden, gilt der Koeffizientengesamtwert einer einzelnen Variable für mehrere korrelierte Variablen, sodass die Koeffizienten für multikollineare Variablen verringert werden. Da die restlichen Koeffizientenwerte durch die Normalisierung sanktioniert werden, erhöht sich die Wahrscheinlichkeit, dass die Koeffizienten multikollinearer Variablen auf Null reduziert und aus dem Modell entfernt werden.

Definieren eines Untersuchungsgebiets

Wenn die Eingabe-Punkt-Features keine Hintergrundpunkte enthalten, muss ein Untersuchungsgebiet angegeben und definiert werden, wo Vorhandensein möglich ist. Sie können zum Definieren des Untersuchungsgebiets drei Optionen des Parameters Untersuchungsgebiet verwenden:

• Konvexe Hülle: Verwendung der konvexen Hülle der Eingabe-Punkt-Features.

  

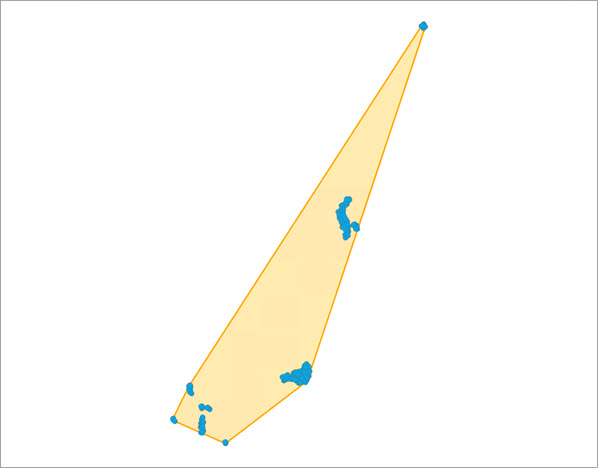
• Raster-Ausdehnung: Die Ausdehnung des Schnittpunktes der im Parameter Erklärende Trainings-Raster angegebenen Raster.

  

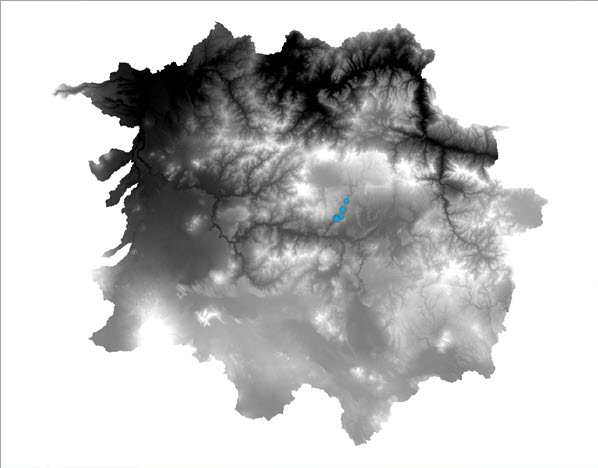
• Untersuchungsgebiet-Polygon: Verwendung einer angepassten Polygon-Feature-Class-Grenze, die im Parameter Untersuchungsgebiet-Polygon angegeben wird.

  

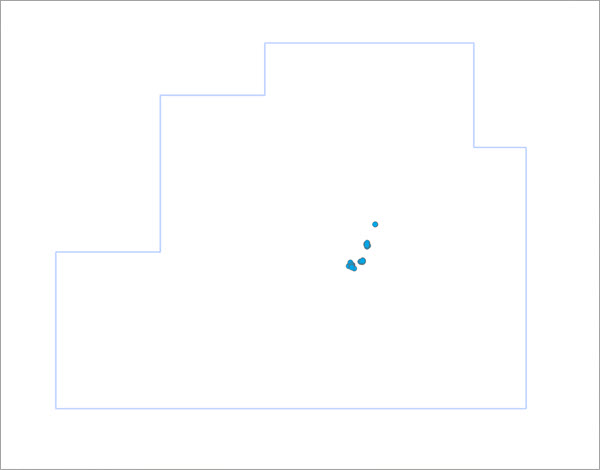
Das Untersuchungsgebiet hat erheblichen Einfluss auf das Ergebnis des Modells: Die Ausdehnung des Untersuchungsgebiets bestimmt die Raster-Zellen aus den erklärenden Trainings-Rastern, die zum Erstellen der Hintergrundpunkte verwendet werden. Die Hintergrundpunkte bestimmen die Umgebungsbedingungen, unter denen Vorhandensein möglich ist und werden mit den Umgebungsbedingungen verglichen, in denen Vorhandensein festgestellt wird. Die Vorhersageergebnisse unterscheiden sich, wenn sich das Verhältnis zwischen der Anzahl an Hintergrundpunkten und Punkten des Vorhandenseins ändert.

Das Untersuchungsgebiet bestimmt die Ausdehnung der Trainingsdaten für das Modell. In diesem Szenario stellen die Eingabe-Punkt-Features dar, wo Vorhandensein festgestellt wurde, und das Untersuchungsgebiet stellt dar, wo Vorhandensein möglich ist (auch wenn sie nicht unbedingt festgestellt wurde). Es wird empfohlen, das Untersuchungsgebiet für eine Analyse am Survey-Design der erfassten Punkte des Vorhandenseins auszurichten. Wenn z. B. in einem Survey für die Erfassung von Daten zum Vorhandensein eine Region in der Größe von 100 Quadratkilometern gründlich untersucht wurde, kann das Begrenzungspolygon der Region als Untersuchungsgebiet verwendet werden.

In manchen Fällen ist es möglicherweise hilfreich, unterschiedliche Untersuchungsgebiete für eine Reihe von Eingabe-Punkt-Features zu verwenden, um unterschiedliche Dynamiken eines Phänomens zu untersuchen (Elith et al. 2011, 51–52).

Reduzieren der Stichprobenverzerrung mithilfe von räumlicher Ausdünnung

Eine Stichprobenverzerrung tritt auf, wenn in den Eingabe-Punkt-Features dargestellte Stichprobengebiete bestimmte räumliche Muster aufweisen. Beispielsweise werden Datenerfassungs-Surveys i. d. R. näher an Straßen, Wegen und anderen Gegebenheiten durchgeführt, die die Datenerfassung begünstigen. Die Stichprobenverzerrung bewirkt, dass Daten, die das Vorhandensein eines Phänomens darstellen sollen, mit Daten vermengt werden, die zeigen, dass geeignete Bedingungen für die Datenerfassung vorliegen. In den meisten auf Vorhandensein beschränkten Datasets kommt es zwangsläufig zu Stichprobenverzerrung. Diese lässt sich nur in äußerst strikten und strukturierten Survey-Designs reduzieren.

Durch räumliche Ausdünnung können die Auswirkungen der Stichprobenverzerrung im Modell verringert werden. Dabei werden Punkte des Vorhandenseins und Hintergrundpunkte aus den Trainingsdaten entfernt, sodass die angegebene Entfernung zwischen den Punkten minimal ist. Indem die Anzahl der Punkte innerhalb einer angegebenen Entfernung zwischen den Punkten reduziert wird, werden in den Trainingsdaten für das Modell Flächen verringert, die das räumlich notwendige Maß an Stichproben überschreiten.

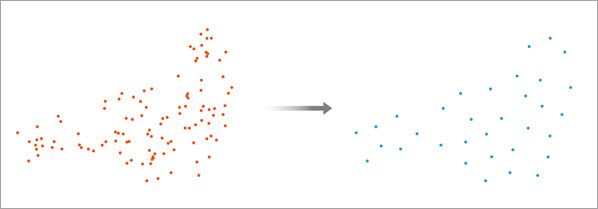
Aktivieren Sie für die Verwendung von räumlicher Ausdünnung den Parameter Räumliche Ausdünnung anwenden, und geben Sie Werte für die folgenden beiden Parameter an:

• Minimale Entfernung zum nächsten Nachbarn: Legt die minimal zulässige Entfernung zwischen zwei Punkten fest.
• Anzahl der Iterationen für die Ausdünnung: Legt fest, wie oft versucht werden soll, Punkte zu entfernen, um eine geeignete Lösung zu finden. Nachdem diese Anzahl der Ausführungen von räumlicher Ausdünnung erfolgt ist, wird im Trainingsmodell die Ausführung verwendet, bei der die größte Anzahl an Punkten übrig geblieben ist.

Die räumliche Ausdünnung erfolgt für Punkte des Vorhandenseins und Hintergrundpunkte, auch wenn das Werkzeug bei Verwendung von auf Vorhandensein beschränkten Daten Hintergrundpunkte generiert. Die räumliche Ausdünnung der Hintergrundpunkte erfolgt getrennt von der räumlichen Ausdünnung der Punkte des Vorhandenseins. Dies kann dazu führen, dass die Entfernung eines Punktes des Vorhandenseins zu einem Hintergrundpunkt geringer als die minimale Entfernung zum nächsten Nachbarn ist.

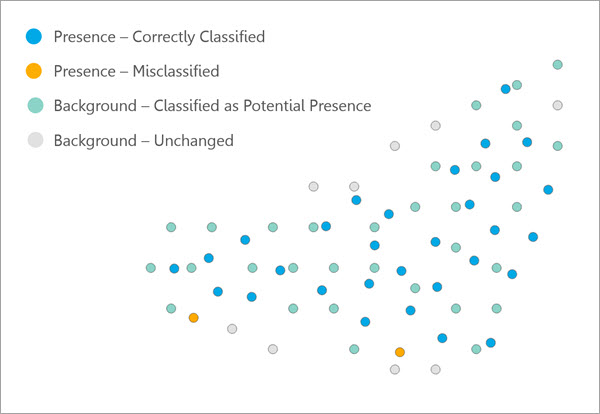
Wenn mit dem Werkzeug Hintergrundpunkte mithilfe von Raster-Zellen erstellt werden, wird räumliche Ausdünnung angewendet durch Resampling des Rasters mit dem Parameterwert Minimale Entfernung zum nächsten Nachbarn und durch Verwendung der resultierenden Raster-Zellenschwerpunkte als räumlich ausgedünnte Hintergrundpunkte.

Die räumliche Ausdünnung kann hilfreich sein, um Probleme aufgrund von Rastern mit einer hohen Anzahl an Zellen zu reduzieren, da die Anzahl der Hintergrundpunkte verringert wird. Unabhängig von der Raster-Auflösung bleibt nach der Ausdünnung ungefähr die gleiche Anzahl an Hintergrundpunkten gemäß der angegebenen minimalen Entfernung zum nächster Nachbarn erhalten.

Räumliche Ausdünnung wird nicht angewendet, wenn der Wert der minimalen Entfernung zum nächsten Nachbarn kleiner ist als die kürzeste Entfernung zwischen zwei beliebigen Punkten (aus Eingabe-Punkt-Features oder von Raster-Zellenschwerpunkten abgeleitet), da die Daten den Kriterien für räumliche Ausdünnung entsprechen.

Konfigurieren des Modells

Das Werkzeug enthält verschiedene Parameter zum Konfigurieren und Anpassen des Modells. Zum Ausführen des Werkzeugs ist es nicht erforderlich, jeden Parameter zu verwenden. Die Nützlichkeit des Werkzeugs für Ihre Workflows zur Modellierung des Vorhandenseins lässt sich jedoch erheblich verbessern, wenn Sie die Funktionsweise des Modells und die Verwendung jedes Parameters begreifen.

Festlegen der relativen Gewichtung des Vorhandenseins zum Hintergrund

Das Werkzeug legt mit dem Parameter Relative Gewichtung des Vorhandenseins zu Hintergrund fest, wie Hintergrundpunkte vom Modell berücksichtigt werden.

Der Standardwert 100 bedeutet, dass Punkte des Vorhandenseins in den Eingabe-Punkt-Features die primäre Quelle der Informationen zum Vorhandensein sind. Das Vorkommen der einzelnen Hintergrundpunkte ist unbekannt, und diese können lediglich zum Darstellen von Landschaftseigenschaften verwendet werden, wenn Vorhandensein möglich, jedoch unbekannt ist. Der Wert 1 bedeutet, dass Hintergrundpunkte die gleiche Aussagefähigkeit wie Punkte des Vorhandenseins haben. Da sie keine Punkte des Vorhandenseins sind, jedoch die gleiche Aussagefähigkeit besitzen, stellen sie bekannte Positionen des Fehlens dar. Hintergrundpunkte als Positionen des Fehlens können dann gleichwertig und gemeinsam mit Positionen des Vorhandenseins zum Erstellen eines binären Klassifizierungsmodells verwendet werden, das Vorhandensein und Fehlen schätzt.

Dieser Wert wirkt sich erheblich auf die Funktion des Modells und die resultierenden Vorhersagen des Werkzeugs aus. Wenn der Wert von Relative Gewichtung der Vorhandenseins zu Hintergrund nahe 100 ist, wendet das Modell die herkömmliche Form der MaxEnt-Methode an. Wenn der Wert 1 lautet, behandelt das Modell jeden Punkt des Vorhandenseins und Hintergrundpunkt gleich und ähnelt der logistischen Regression.

Es wird empfohlen, geeignete Werte zwischen 1 und 100 für den Parameter Relative Gewichtung des Vorhandenseins zu Hintergrund auf Grundlage Ihres Fachwissens zu wählen, da sie als Darstellung der Verbreitung des Ereignisses im Untersuchungsgebiet betrachtet werden können.

Verwenden von Kopplungsfunktionen und Wahrscheinlichkeitsschwellenwerten für Vorhandensein zum Interpretieren von Ausgaben

Eine Zwischenausgabe des Modells (nicht vom Werkzeug zurückgegeben) ist die relative Häufigkeit (Relative Occurrence Rate, ROR) für jede Position. Diese Zwischenausgabe stellt keine Vorkommenswahrscheinlichkeit dar. Sie entspricht der relativen Eignung jeder Position für das Fördern des Vorhandenseins im Untersuchungsgebiet. Um diese Raw-Werte in Werte, die sich als Wahrscheinlichkeiten und Vorhersagen des Vorhandenseins auswerten lassen, umzuwandeln, müssen Sie in den Parametern Transformation der Wahrscheinlichkeit für Vorhandensein (Kopplungsfunktion) und Grenzwert für Wahrscheinlichkeit für Vorhandensein eine Kopplungsfunktion und einen Grenzwert angeben.

Im Parameter Transformation der Wahrscheinlichkeit für Vorhandensein (Kopplungsfunktion) sind zwei Optionen verfügbar:

• C-log-log: Berechnet die Wahrscheinlichkeit des Vorhandenseins an jeder Position mit der Formel 1 - exp (- exp (Entropie + Raw-Wert-Ausgabe)). Dies ist die Standardeinstellung.

• Logistisch: Berechnet die Wahrscheinlichkeit des Vorhandenseins an jeder Position mit der Formel 1 / (1 + exp (- Entropie - Raw-Wert-Ausgabe)).

Kopplungsfunktionen stehen im Zusammenhang mit der Mehrdeutigkeit, die Punktdatensätze für Vorhandensein u. U. aufweisen. Verwenden Sie die Option C-log-log, wenn die Position und das Vorhandensein eines Phänomens klar und eindeutig sind. Dies ist beispielsweise der Fall, wenn die Punkte des Vorhandenseins eine unbewegliche Pflanzenart darstellen. Verwenden Sie die Option Logistisch, wenn die Position und das Vorhandensein eines Phänomens nicht eindeutig sind. Dies ist beispielsweise der Fall, wenn die Punkte des Vorhandenseins Positionen einer wandernden Tierart darstellen.

Die mit einer Kopplungsfunktion berechnete Wahrscheinlichkeit des Vorhandenseins wird als Wert zwischen 0 und 1 angegeben. Mit dem Parameter Grenzwert für Wahrscheinlichkeit für Vorhandensein können Sie einen Wahrscheinlichkeitsschwellenwert angeben, der eine Position als Vorhandensein klassifiziert. Der Standardwert ist 0,5, und Werte größer als oder gleich 0,5 werden als Vorhandensein klassifiziert. Sie können einen Wert zwischen 0,01 und 0,99 angeben, um einen benutzerdefinierten Wert festzulegen.

Die mit dem Grenzwert erzielten Klassifizierungsergebnisse werden mit bekannten Punkten des Vorhandenseins in den Eingabe-Punkt-Features verglichen, und in den Geoverarbeitungsmeldungen und den trainierten Ausgabe-Features werden Diagnosen bereitgestellt.

Angeben von Modelltrainingsausgaben

Das Werkzeug organisiert Ausgaben in Trainings- und Vorhersageausgaben. Der Hauptunterschied besteht darin, dass Trainingsausgaben den Daten entsprechen, die beim Trainieren und der Auswahl des Modells verwendet wurden, während Vorhersageausgaben den Daten entsprechen, auf die das Modell noch nicht angewendet wurde.

Trainierte Ausgabe-Features

Erzeugen Sie mit dem Parameter Trainierte Ausgabe-Features eine Feature-Class, die die beim Trainieren des Modells verwendeten Punkte enthält. Diese Ausgabe symbolisiert jeden trainierten Punkt mithilfe eines Vergleichs zwischen der Klassifizierung durch das Modell und der beobachteten Klassifizierung.

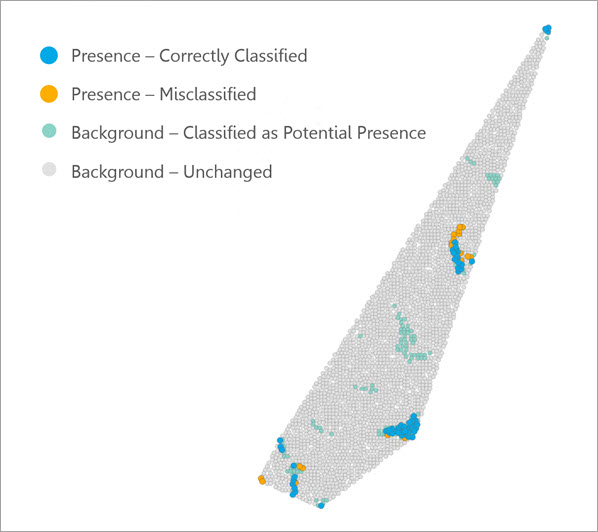
Die Punkte in den trainierten Ausgabe-Features sind nicht unbedingt mit den Punkten in den Eingabe-Punkt-Features identisch, da Hintergrundpunkte generiert werden, wenn auf Vorhandensein beschränkte Daten verwendet werden, und die Anzahl der beim Trainieren des Modells verwendeten Punkte möglicherweise durch räumliche Ausdünnung verringert wird.

Die trainierten Ausgabe-Features enthalten drei Diagramme:

• Prozentsätze der Klassifizierungsergebnisse: Wird verwendet, um anhand der beobachteten Klassifizierung in den Trainings-Features den Anteil richtiger Vorhersagen zu schätzen.

  

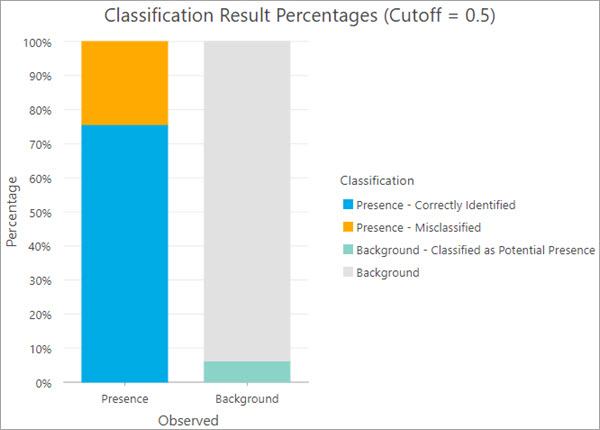
• Anzahl für Vorhandensein und Hintergrund nach Wahrscheinlichkeitsbereichen: Wird verwendet, um die Verteilung der Wahrscheinlichkeitswerte für das Vorhandensein im Modell mit den beobachteten Klassifizierungen von Vorhandensein und Hintergrund zu vergleichen.

  

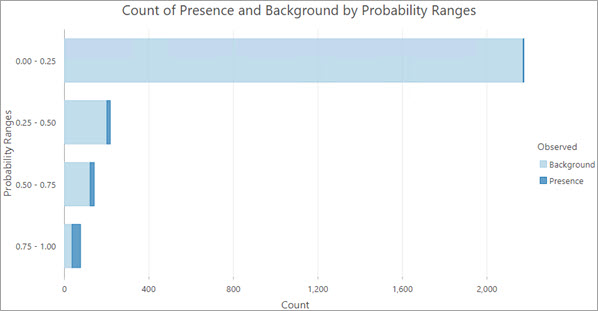
• Verteilung der Wahrscheinlichkeit für Vorhandensein nach Klassifizierungen: Wird verwendet, um die Verteilung der Wahrscheinlichkeitsbereiche für Vorhandensein nach Klassifizierungsbezeichnung anzuzeigen.

  

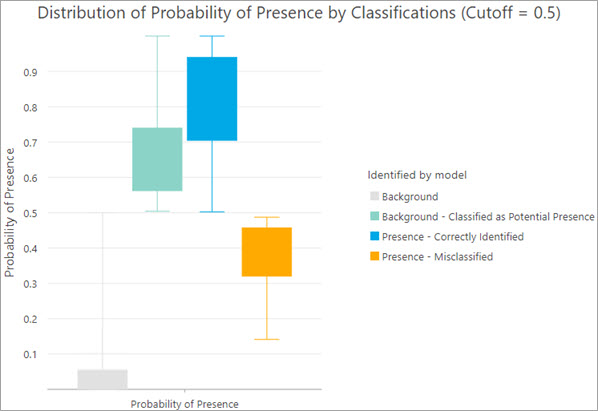
Trainiertes Ausgabe-Raster

Sie können mit Trainiertes Ausgabe-Raster ein Raster erstellen, das die Wahrscheinlichkeit des Vorhandenseins in jeder Zelle in der Ausdehnung der Eingabe-Trainingsdaten in vier Kategorien klassifiziert. Diese Option ist nur verfügbar, wenn Eingabe-Punkt-Features verwendet werden, die keine Hintergrundpunkte enthalten.

Die Ausdehnung des trainierten Ausgabe-Rasters entspricht dem Schnittpunkt der erklärenden Trainings-Raster im Untersuchungsgebiet. Die Standard-Zellengröße ist die maximale Zellengröße der Raster-Eingaben. Diese können Sie mit der Umgebung Zellengröße ändern.

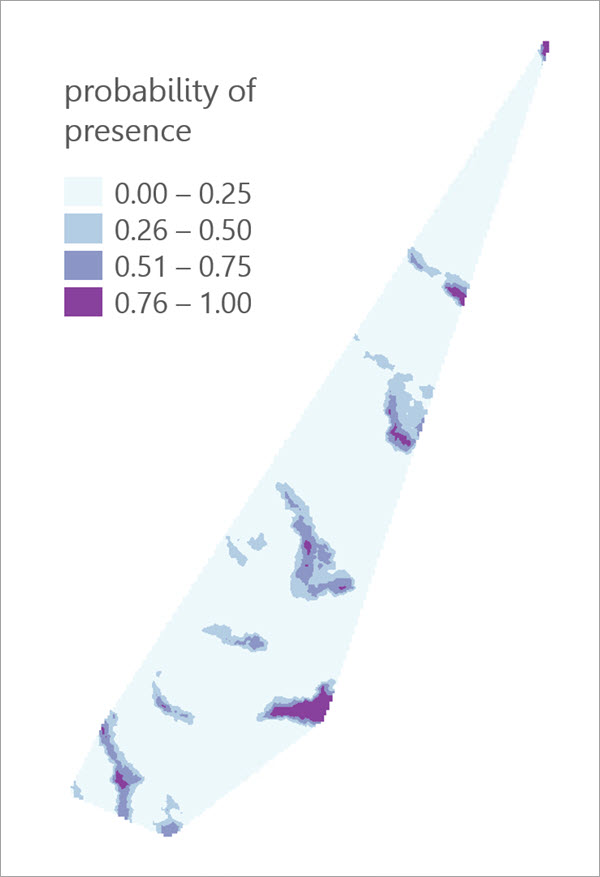
Antwortkurventabelle und Empfindlichkeitstabelle

Sie können mit dem Parameter Ausgabe-Antwortkurventabelle eine Tabelle mit Diagrammen erstellen, die die marginale Auswirkung der erklärenden Variable auf die Vorhersage des Vorhandenseins visualisieren. Dies wird auch als partielle Abhängigkeit (oder partielle Antwort) des Vorhandenseins des Phänomens in Bezug auf die jeweilige erklärende Variable bezeichnet.

Das Diagramm Teilantwort von kontinuierlichen Variablen besteht aus mehreren Diagrammen. Jedes Diagramm visualisiert die Auswirkungen sich ändernder Werte in jeder erklärenden Variablen auf die Wahrscheinlichkeit des Vorhandenseins, während alle anderen Faktoren unverändert bleiben.

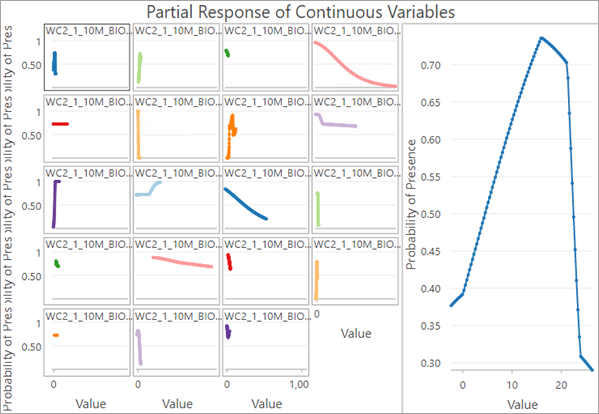
Das Diagramm "Teilantwort von Kategorievariablen" ist ein Diagramm mit einem Balken, das die marginale Antwort des Vorhandenseins für jede erklärende Variablenkategorie anzeigt.

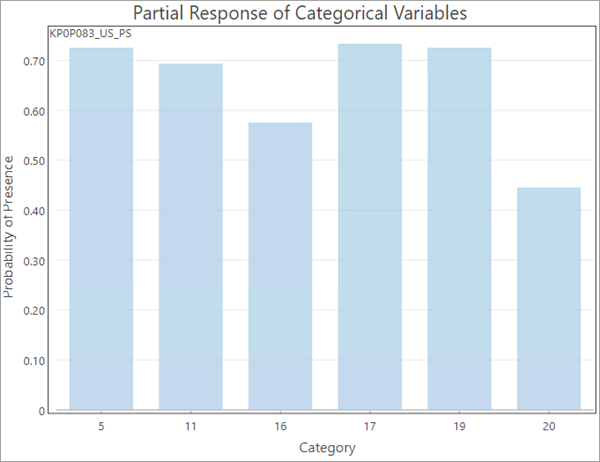
Mit dem Parameter Ausgabe-Empfindlichkeitstabelle wird eine Tabelle bereitgestellt, die zwei Diagramme enthält:

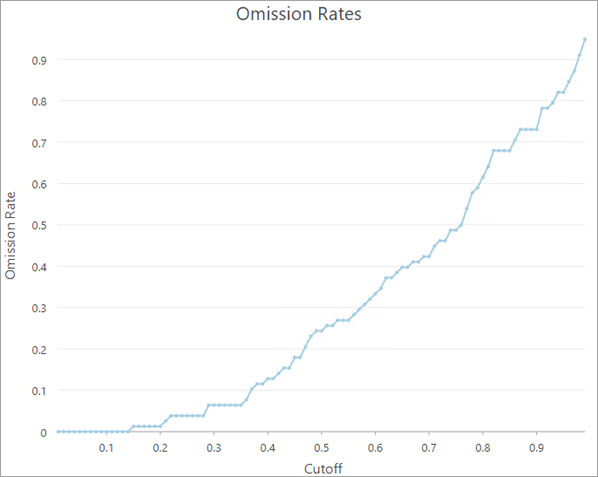
• Diagramm Auslassungsraten: Wird verwendet, um den Anteil bekannter Punktes des Vorhandenseins zu schätzen, die vom Modell fälschlicherweise als Fehlen klassifiziert wurden. Dabei werden Grenzwerte für die Wahrscheinlichkeit für Vorhandensein im Bereich zwischen 0 und 1 verwendet.

  

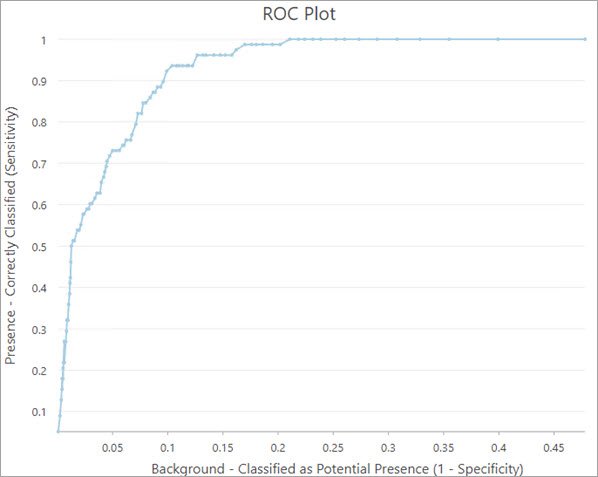
• Diagramm ROC-Plot: Wird verwendet, um den Anteil richtig klassifizierter bekannter Punkte des Vorhandenseins, auch als Empfindlichkeit des Modells bezeichnet, und den Anteil der als Vorhandensein klassifizierten Hintergrundpunkte zu vergleichen. Dieser Vergleich erfolgt wie beim Diagramm Auslassungsraten über einen Bereich von Grenzwerten für die Wahrscheinlichkeit für Vorhandensein zwischen 0 und 1.

  

Anwenden des Modells zu Vorhersagezwecken

Das Werkzeug Auf Vorhandensein beschränkte Vorhersage wird nicht nur zum Trainieren von Modellen, sondern auch zum Schätzen des Vorhandenseins an neuen Positionen mithilfe von Parametern in der Parameterkategorie Vorhersageoptionen verwendet.

Konfigurieren des Werkzeugs für Vorhersagen mithilfe neuer Eingabe-Vorhersage-Features

Der Parameter Eingabe-Vorhersage-Features gibt Positionen an, an denen das Werkzeug das trainierte Modell anwendet, um Vorhandensein zu schätzen. Der Parameter Ausgabe-Vorhersage-Features gibt eine Ausgabe an, in der die Ergebnisse der auf den Wert des Parameters Eingabe-Vorhersage-Features angewendeten Vorhersage enthalten sind.

Sie müssen für jede erklärende Variable, die beim Trainieren des Modells verwendet wird, eine abgeglichene erklärende Variable in Form eines Feldes, eines Entfernungs-Features oder eines Rasters angeben. Verwenden Sie hierzu den Parameter Erklärende Variablen abgleichen, Entfernungs-Features abgleichen bzw. Erklärende Raster abgleichen.

Die Wertebereiche der Vorhersagedaten können von den Wertebereichen der Trainingsdaten abweichen. Beispielsweise kann ein Höhen-Raster zum Trainieren des Modells Werte zwischen 400 und 1.000 Metern enthalten, während das entsprechende Höhen-Raster für die Vorhersagepositionen Flächen mit Höhen zwischen 200 und 1.200 Metern enthält. Die Wertebereiche der erklärenden Variable für Vorhersagepositionen sollten nach Möglichkeit mit den Wertebereichen der Trainingsdaten übereinstimmen. Mit dem Parameter Vorhersagen außerhalb von Datenbereichen zulassen kann das Modell jedoch extrapolieren und auch für diese Positionen Schätzungen bereitstellen. Verwenden Sie die Geoverarbeitungsmeldungen des Werkzeugs, um zu ermitteln, ob die Wertebereiche der Trainingsdaten die Wertebereiche der erklärenden Variable überschritten haben.

Sie können auch mit dem Parameter Ausgabe-Vorhersage-Raster ein Raster erstellen, das die Ergebnisse der Vorhersagen des Modells enthält, die auf jede Zelle in der Ausdehnung des Schnittpunktes der im Parameter Erklärende Raster abgleichen angegebenen Raster angewendet wurden. Mit diesem Parameter wird eine vorhergesagte Oberfläche über der Ausdehnung der für die Vorhersagepositionen verfügbaren Umgebungsbedingungen bereitgestellt.

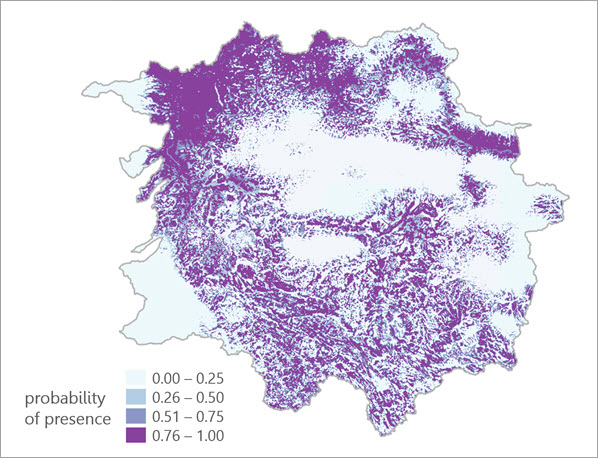
Das Ausgabe-Vorhersage-Raster unterscheidet sich vom Ausgabe-Trainings-Raster. Letzteres wird nur für die Ausdehnung der im Modell verwendeten Trainingsdaten verwendet, und das Vorhersage-Raster wird für die Ausdehnung der Eingabe-Vorhersage-Features und des Schnittpunktes der abgeglichenen erklärenden Raster generiert.

Validieren des Modells

Das Werkzeug bietet Optionen zum Überprüfen und Bewerten eines Modells. Es wird empfohlen, diese Optionen zusammen mit den Parametern Ausgabe-Antwortkurventabelle und Ausgabe-Empfindlichkeitstabelle zu verwenden, um die Qualität und Nützlichkeit des Modells zu bewerten.

Verwenden von Resampling und Kreuzvalidierung

Die Parameter Resampling-Schema und Gruppenanzahl in der Parameterkategorie Validierungsoptionen geben an, ob eine Kreuzvalidierung des Modells durchgeführt wird.

Wenn das Resampling-Schema Zufallsprinzip ausgewählt wird, unterteilt das Werkzeug die Trainingsdaten in die angegebene Anzahl von Gruppen.

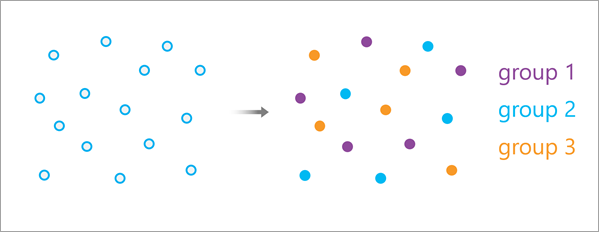
Anschließend durchläuft das Werkzeug die einzelnen Gruppen. Dabei werden die Daten für die aktuelle Gruppe als Validierungs-Subset und die Sammlung der Daten für alle verbleibenden Gruppen als Trainings-Subset ausgewählt.

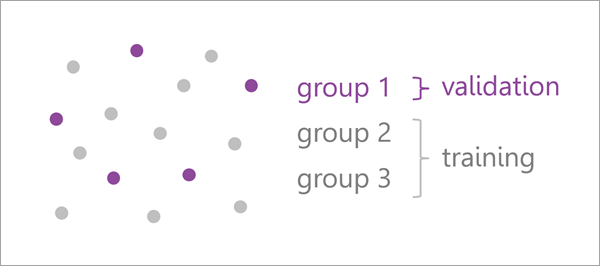
Das Werkzeug erstellt mithilfe des Trainings-Subsets für die Gruppe ein Modell und sagt für jedes Validierungs-Feature das Vorhandensein vorher. Anschließend werden die Ergebnisse der Vorhersage mit dem bekannten Vorhandensein und den Hintergrundbezeichnungen im Validierungs-Subset verglichen.

Dieser Prozess wird fortgesetzt, indem die einzelnen Gruppen durchlaufen werden und jeweils die Rolle des Validierungs-Subsets übernehmen. Der Prozess wird allgemein als "k-fache Kreuzvalidierung" bezeichnet, wobei "k" der Anzahl der Gruppen entspricht.

Für jede Gruppe wird der Prozentsatz der richtig klassifizierten Vorhandensein-Features und der Prozentsatz der als potenzielles Vorhandensein klassifizierten Hintergrund-Features erfasst. Anhand der Diagnosedaten der einzelnen Gruppen kann bestimmt werden, wie gut das Modell das Vorhandensein an unbekannten Positionen schätzen kann. Diese Diagnosedaten sind in den Geoverarbeitungsmeldungen des Werkzeugs enthalten.

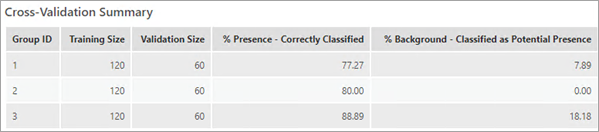
Zum Erstellen eines Modells für die Kreuzvalidierung mit dem Werkzeug muss das Trainings-Subset für jede Gruppe mindestens zwei Punkte des Vorhandenseins und zwei Hintergrundpunkte enthalten. Wenn sich mit den vom Werkzeug nach dem Zufallsprinzip ausgewählten Gruppen nicht mindestens zwei Punkte des Vorhandenseins und zwei Hintergrundpunkte aus den Trainings-Subsets der einzelnen Gruppen ergeben, versucht das Werkzeug, die Gruppen neu zu erstellen, bis diese Anforderung erfüllt ist oder mindestens zehn Versuche unternommen wurden. Wenn diese Anforderung auch nach zehn Versuchen mithilfe der bereitgestellten Daten nicht erfüllt ist, wird eine Warnung angezeigt, aus der hervorgeht, dass die Kreuzvalidierung nicht möglich war.

Geoverarbeitungsmeldungen

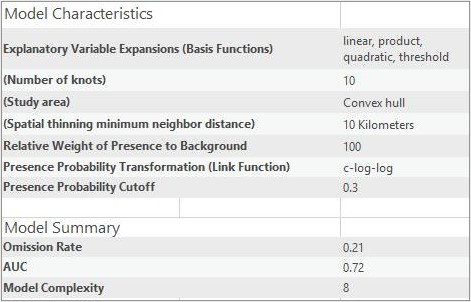
Eine wichtige Ausgabe des Werkzeugs ist der Bericht in den Geoverarbeitungsmeldungen. Der Bericht enthält wichtige Informationen zum trainierten Modell. Hierzu zählen eine Tabelle mit Modellparametern, Modellvergleichsdiagnosen, Regressionskoeffizienten, eine Zusammenfassung der Kategorien (falls unter den erklärenden Variablen Kategorievariablen vorhanden sind), eine Zusammenfassung der Kreuzvalidierung (für das Resampling-Schema "Zufallsprinzip") und eine Diagnose des Bereichs der erklärenden Variable für Trainings- und Vorhersagedaten (wenn Eingabe-Vorhersage-Features verwendet wurden).

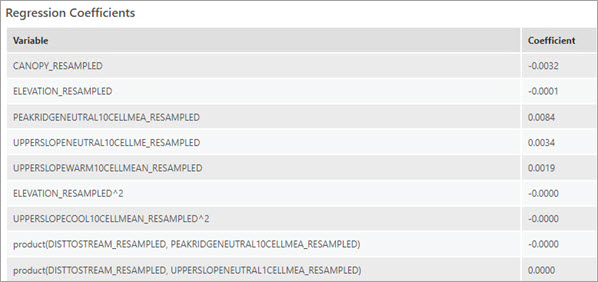
Die Tabelle Regressionskoeffizienten zeigt die erklärenden Variablen, die für das Training des Modells nach der Vereinfachung verwendet werden. Jeder Eintrag enthält den Namen einer erklärenden Variablen, die entsprechende Basis-Erweiterung und den resultierenden Koeffizienten. Die Namen der erklärenden Variablen geben die Art der Basis-Erweiterung an. Beispielsweise lautet der Name einer Produktvariable, die sich aus dem Produkt einer Elevation-Variablen und einer ClimaticWaterDeficit -Variablen zusammensetzt, product(ELEVATION, CLIMACTICWATERDEFICIT). Koeffizienten werden auf vier Dezimalstellen gerundet.

Die Tabelle Zusammenfassung der Kreuzvalidierung enthält die ID jeder Kreuzvalidierungsgruppe, die Anzahl der Beobachtungen in ihren Trainingsvalidierungs-Subsets, den Prozentsatz der beobachteten Vorhandensein-Features, die als Vorhandensein vorhergesagt wurden, und den Prozentsatz der beobachteten Hintergrund-Features, die als Hintergrund vorhergesagt wurden.

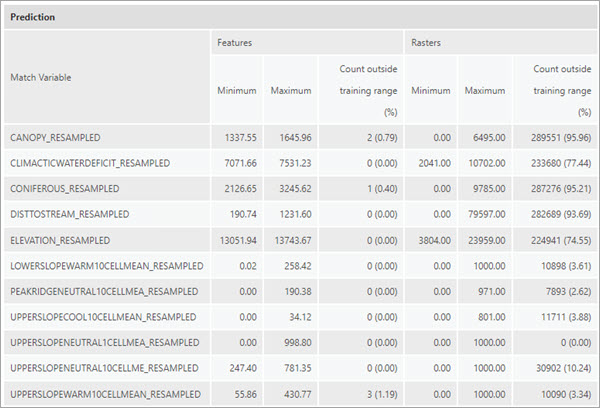
Die Tabelle Diagnose des Bereichs der erklärenden Variable enthält jede bereitgestellte erklärende Variable (in Form eines Feldes, eines Entfernungs-Features oder eines Rasters), ihren Minimal- und Maximalwert in den Trainingsdaten und (sofern Eingabe-Vorhersage-Features verwendet werden) den Minimal- und Maximalwert in den Vorhersagedaten.

Empfehlungen und Überlegungen

Bei Verwendung des Werkzeugs sollten verschiedene Empfehlungen und Überlegungen beachtet werden.

Multikollinearität

Durch die Normalisierungsfunktion des Werkzeugs werden die Auswirkungen von Multikollinearität in den erklärenden Variablen reduziert. Dennoch wird empfohlen, die korrelierten erklärenden Variablen zu ermitteln und ihre Anzahl zu verringern. Zu den gängigen Werkzeugen für die Analyse von Multikollinearität zählen Scatterplotmatrix-Diagramme, Regressionsanalyse und Dimensionsreduktion.

Kategoriedaten

Wenn für den Parameter Resampling-Schema die Option Zufallsprinzip ausgewählt wird, unterteilt das Werkzeug die Eingabe-Trainingsdaten in Gruppen, um eine Kreuzvalidierung durchzuführen. Wenn in diesem Fall in den resultierenden Gruppen Kategorien mit weniger als drei Datenpunkten vorhanden sind, kann keine Kreuzvalidierung erfolgen, und Sie werden durch eine Warnung benachrichtigt, dass die Resampling-Methode nicht angewendet werden konnte. Die Wahrscheinlichkeit dieses Problems lässt sich verringern, indem das Werkzeug mit einem niedrigeren Wert für den Parameter Gruppenanzahl ausgeführt wird. Dadurch werden die einzelnen Gruppen vergrößert, und es erhöht sich die Wahrscheinlichkeit, dass Kategorien in jeder Gruppe enthalten sind.

Räumliche Ausdünnung

Verwenden Sie den Parameter Trainierte Ausgabe-Features, um die Ergebnisse der räumlichen Ausdünnung für den Wert von Eingabe-Punkt-Features zu untersuchen.

Geben Sie in den Parametern Eingabe-Punkt-Features und Eingabe-Vorhersage-Features die gleichen Features an, um ein Modell mithilfe von räumlicher Ausdünnung zu erstellen und das Modell auf alle Eingabe-Punkt-Features anzuwenden.

Wahrscheinlichkeitsgrenzwert

Verwenden Sie die Diagramme Auslassungsraten und ROC-Plot, um einen geeigneten Wert für den Parameter Grenzwert für die Wahrscheinlichkeit für Vorhandensein zu bestimmen.

Das Diagramm Auslassungsraten stellt visuell dar, wie verschiedene Werte des Parameters Grenzwert für die Wahrscheinlichkeit für Vorhandensein zu einer jeweils unterschiedlichen Anzahl fehlklassifizierter Punkte des Vorhandenseins führen (auch als Auslassungsrate bezeichnet). Die Auslassungsrate sollte nach Möglichkeit nahe 0 sein. Jedoch darf der Grenzwert nicht einfach verringert werden, um eine möglichst geringe Auslassungsrate zu erreichen, da hierdurch auch die Anzahl der Hintergrundpunkte minimiert wird, die als potenzielles Vorhandensein klassifiziert werden (in vielen Szenarien ein hilfreiches Ergebnis).

Verwenden Sie das Diagramm ROC-Plot, um zu ermitteln, wie sich unterschiedliche Grenzwerte auf die Anzahl der als Vorhandensein klassifizierten Hintergrundpunkte auswirken. Das Diagramm bietet einen Vergleich zwischen richtig klassifizierten Punkten des Vorhandenseins und als potenzielle Punkte des Vorhandenseins klassifizierten Hintergrundpunkten für unterschiedliche Grenzwerte für die Wahrscheinlichkeit für Vorhandensein.

Der Zweck des Diagramms ROC-Plot ist je nach Art der Hintergrundpunkte unterschiedlich. Wenn Hintergrundpunkte das Fehlen des Vorkommens darstellen und der Wert des Parameters Relative Gewichtung des Vorhandenseins zu Hintergrund 1 beträgt, kann das Diagramm als herkömmlicher ROC-Plot verwendet werden, in dem die Empfindlichkeit (richtig klassifizierte Punkte des Vorhandenseins) maximiert und die 1-Spezifität (Hintergrund oder Fehlen, der bzw. das als Vorhandensein klassifiziert ist) minimiert ist. In diesem Fall sind Grenzwerte nahe an der oberen linken Ecke des Diagramms besser geeignet. Wenn Hintergrundpunkte unbekanntes, jedoch mögliches Vorkommen darstellen, veranschaulicht der ROC-Plot die Auswirkung unterschiedlicher Grenzwerte auf die Anzahl der potenziellen Hintergrundpositionen, die als Vorhandensein geschätzt wurden.

Es wird empfohlen, beide Diagramme gemeinsam zu verwenden. Wenn Sie das Diagramm "Auslassungsraten" für den Standardgrenzwert 0,5 auswerten, wählen Sie im Diagramm Auslassungsraten den Grenzwertkandidaten aus, und vergleichen Sie diesen Eintrag im Diagramm ROC-Plot.

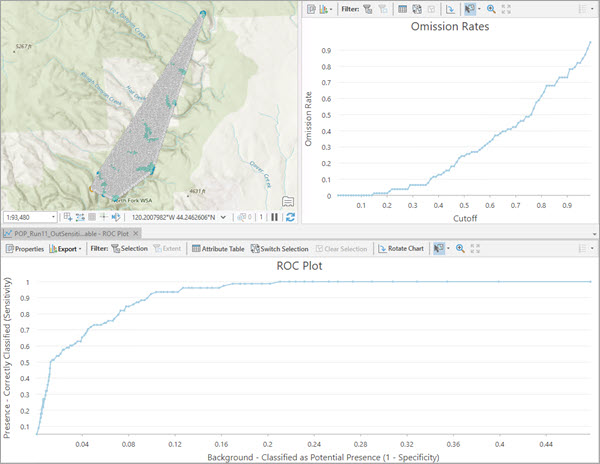
Diagramme für trainierte Ausgabe-Features zur Validierung

Im Diagramm Prozentsätze der Klassifizierungsergebnisse wird ein Vergleich der beobachteten und vorhergesagten Klassifizierungen angezeigt. Sie können mit dem Diagramm die Fähigkeit des Modells zum Vorhersagen der Performance an bekannten Punkten des Vorhandenseins bewerten. Sie können z. B. die Performance des Modells beim Vorhersagen des Vorhandenseins an bekannten Punkten des Vorhandenseins bewerten, indem Sie sich auf den Anteil der falsch klassifizierten Punkte des Vorhandenseins konzentrieren. In Anwendungsfällen, in denen die Vorhersage des Vorhandenseins für Hintergrundpunkte wichtig ist, können Sie mithilfe des Diagramms auch die Hintergrundpunkte anzeigen und auswählen, für die Vorhandensein vorhergesagt ist.

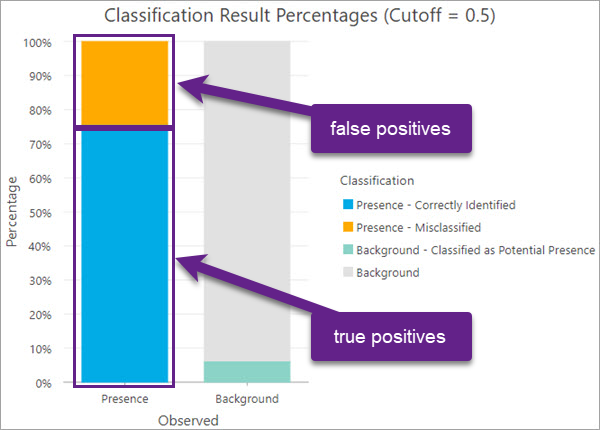
Allgemeine Kriterien für die Modellauswahl

Ein Workflow für die Modellauswahl, der sich für Ihre Anwendungsbeispiele eignen kann, sieht so aus:

1. Bewerten Sie den Standardgrenzwert 0,5 für die Wahrscheinlichkeit für Vorhandensein und seine Auswirkung auf die Fähigkeit des Modells zum Identifizieren bekannter Positionen des Vorhandenseins als Vorhandensein (Empfindlichkeit) mithilfe der Y-Achse des ROC-Plots.

   Öffnen Sie die Diagramme Auslassungsraten und ROC-Plot nebeneinander. Wählen Sie im Plot der Auslassungsraten den Standardgrenzwert 0,5 für die Wahrscheinlichkeit für Vorhandensein aus, und achten Sie auf die resultierende Empfindlichkeit auf der Y-Achse des ROC-Plots.

   

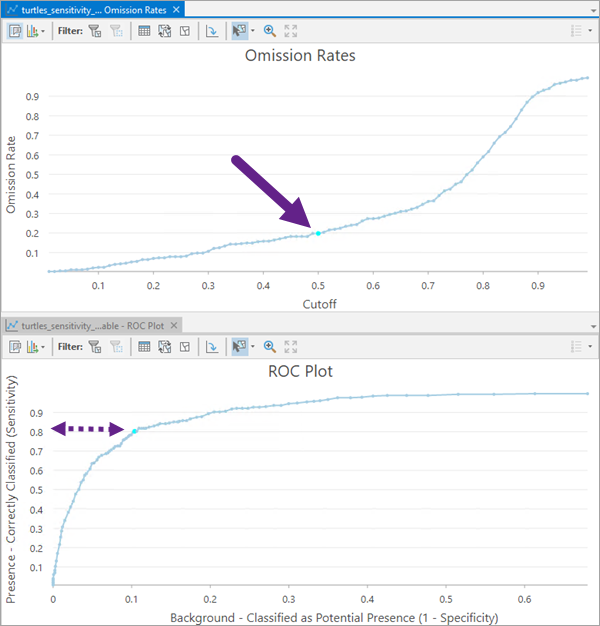
2. Bewerten Sie den Standardgrenzwert 0,5 für die Wahrscheinlichkeit für Vorhandensein und seine Auswirkung auf die Fähigkeit des Modells zum Identifizieren bekannter Hintergrundpositionen als Hintergrund (1-Spezifität) mithilfe der X-Achse des ROC-Plots.

   Öffnen Sie die Diagramme Auslassungsraten und ROC-Plot nebeneinander. Wählen Sie im Plot der Auslassungsraten den Standardgrenzwert 0,5 für die Wahrscheinlichkeit für Vorhandensein aus, und achten Sie auf den resultierenden Wert (1-Spezifität) auf der X-Achse des ROC-Plots.

   Wenn Hintergrundpunkte Positionen mit unbekanntem Vorhandensein darstellen (Verwendung des Standardwertes 100 für den Parameter Relative Gewichtung von Vorhandensein zu Hintergrund), gibt dies den Anteil der Hintergrundpositionen in den übermittelten Trainingsdaten wieder, die voraussichtlich dem potenziellen Vorhandensein entsprechen.

   Wenn Hintergrundpunkte bekanntem Fehlen entsprechen (Verwendung des Wertes 1 für Relative Gewichtung von Vorhandensein zu Hintergrund), gibt dies den Anteil der False Positives wieder (bekannte Positionen des Fehlens, die fälschlich als Vorhandensein beschriftet sind).

   

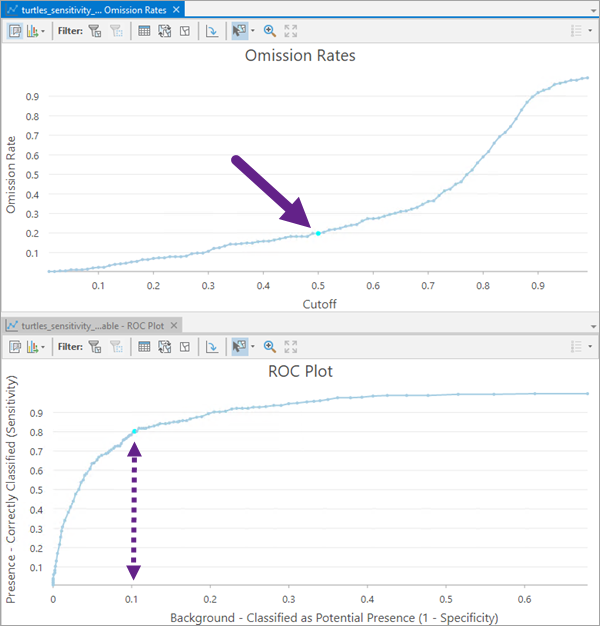
3. Interpretieren Sie die Fläche unter der Kurve (Area Under the Curve, AUC) im ROC-Plot, mit der bewertet werden kann, wie gut das Modell bekannte Positionen des Vorhandenseins als Vorhandensein und bekannte Hintergrundpositionen als Hintergrund schätzen kann. Je höher die Fläche unter der Kurve, umso geeigneter ist das Modell für die Vorhersage des Vorhandenseins.

   

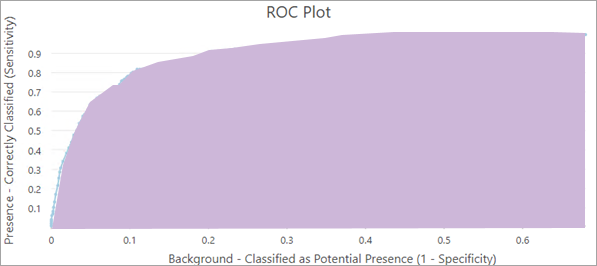
   Während die Fläche unter der Kurve eine hilfreiche allgemeine Bewertungsdiagnose darstellt, ist es wichtig zu entscheiden, ob das Ziel des Modells darin besteht, False Positives zu reduzieren (mit anderen Worten, sicherzustellen, dass das vorhergesagte Vorhandensein mit hoher Wahrscheinlichkeit tatsächlich ein Vorhandensein ist) oder False Negatives zu reduzieren (mit anderen Worten, sicherzustellen, dass das vorhergesagte Fehlen mit hoher Wahrscheinlichkeit tatsächlich ein Fehlen ist). Der ROC-Plot-Wert, der am weitesten links oben im Diagramm angezeigt wird, stellt ein ausgewogenes Verhältnis der beiden Ziele dar.

   

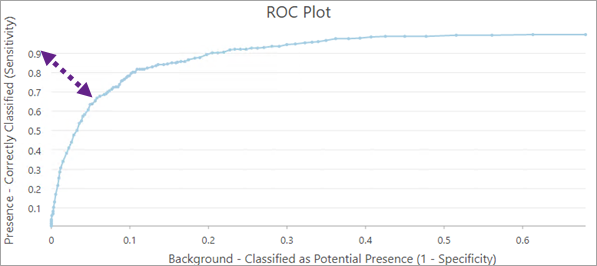
4. Wenn mehrere Modelle ähnliche Validierungsergebnisse liefern, wählen Sie das einfachere Modell. Das Modell mit weniger und einfacheren erklärenden Variablen mag wünschenswert sein, da es besser interpretiert und leichter erklärt werden kann. Aus Gründen der Übersichtlichkeit ist die einfachste Erklärung eines Phänomens in der Regel die beste (Phillips et al., 2006).

   Lassen Sie sich beim Entwurf, bei der Validierung und bei der Verwendung des Modells vor allem von Fachwissen und einem umfassenden Verständnis des Problems leiten.

Zusätzliche Quellen

Weitere Informationen finden Sie in den folgenden Ressourcen:

• Aiello-Lammens, Matthew E., Robert A. Boria, Aleksandar Radosavljevic, Bruno Vilela, Robert P. Anderson. 2015. "spThin: an R package for spatial thinning of species occurrence records for use in ecological niche models". Ecography 38: 541-545.

• Du, Zhaohui, Zhiqiang Wang, Yunxia Liu, Hao Wang, Fuzhong Xue, Yanxun Liu. 2014. "Ecological niche modeling for predicting the potential risk areas of severe fever with thrombocytopenia syndrome." International Journal of Infectious Diseases, 26: 1-8. ISSN 1201-9712. https://doi.org/10.1016/j.ijid.2014.04.006

• Elith, Jane, Steven J. Phillips, Trevor Hastie, Miroslav Dudík, Yung En Chee, and Colin J. Yates. 2011 "A statistical explanation of MaxEnt for ecologists". Diversity and Distributions, 17: 43-57. PDF

• Fithian, William, Jane Elith, Trevor Hastie, David A. Keith. 2014. "Bias Correction in Species Distribution Models: Pooling Survey and Collection Data for Multiple Species". arXiv:1403.7274v2 [stat.AP].

• Fithian, William, Trevor Hastie. 2013. "Finite-sample equivalence in statistical models for presence-only data". The Annals of Applied Statistics Vol. 7, no. 4 (Dezember), 1917-1939.

• Merow, Cory, Matthew J. Smith, and John A. Silander, Jr. 2013. "A practical guide to MaxEnt for modeling species’ distributions: what it does, and why inputs and settings matter". Ecography, 36: 1058-1069. PDF

• Mobley, W., Sebastian, A., Highfield, W., Brody, S. D. 2019. "Estimating flood extent during Hurricane Harvey using maximum entropy to build a hazard distribution model." Journal of Flood Risk Management. 2019;12 (Suppl. 1):e12549. https://doi.org/10.1111/jfr3.12549

• Phillips, Steven J., Miroslav Dudik. 2008. "Modeling of species distributions with Maxent: new extensions and a comprehensive evaluation". Ecography 31: 161-175.

• Phillips, Steven J., Robert P. Anderson, Robert E. Schapire. 2006. "Maximum entropy modeling of species geographic distributions". Ecological Modelling, 190: 231-259. PDF

• Radosavljevic, Aleksandar, Robert P. Anderson. 2014. "Making better Maxent models of species distributions: complexity, overfitting and evaluation". Journal of Biogeography 41, 629-643.