Funktionsweise von "Kontinuierlichen Fluss ableiten"

Für viele Anwendungen ist es von grundlegender Bedeutung zu verstehen, wie sich Wasser durch die Landschaft bewegt, nachdem es in Form von Niederschlag gefallen ist. Digitale Höhenmodelle (DEMs) sind das grundlegende Dataset für die Modellierung des Oberflächenflusses. Diese Daten liefern jedoch keine perfekte Darstellung – häufig gibt es kleine Höhenfehler oder falsche Darstellungen von Landschafts-Features, die den Fluss beeinflussen können.

Daher müssen Sie das Eingabe-DEM vorverarbeiten, bevor Sie die Fließrichtung des Wassers bestimmen können. Unter hydrologischer Aufbereitung versteht man die Modifizierung der Höhenwerte des Eingabe-DEM, um einen kontinuierlichen Oberflächenfluss zu gewährleisten, der dem tatsächlichen Oberflächenfluss entspricht. Die hydrologischer Aufbereitung ist notwendig, wenn das Flussnetz durch DEM-Beschränkungen gestört wird. So können z. B. unkorrekte Höhen als Senken wirken, die den Fluss künstlich akkumulieren und beenden, sodass es unmöglich ist, die Fließrichtung ausgehend von den Senkenzellen zu bestimmen. Brücken, Dämme und unterirdischer Kanäle, die nicht im Oberflächenmodell enthalten sind, können ebenfalls zu fehlerhaften Fließrichtungs- und Akkumulationsausgaben führen.

Das Werkzeug behebt fehlerhafte Fließrichtungs- und Akkumulationsausgaben nicht durch die Änderung der Eingabe-DEM-Daten, sondern durch Anwenden des Algorithmus der kostengünstigsten Route. Der Algorithmus der kostengünstigsten Route schließt die Minimierung der Höhendifferenz bei der Bewegung bergauf über das Eingabe-Oberflächen-Raster. Mit anderen Worten ist ein Optimierungsschritt auf Zellenbasis erforderlich, um den minimalen höher gelegenen Nachbarn zu identifizieren. Zusätzlich werden spezielle Regeln für Senken- und NoData-Zellen angewendet. Senken- oder Muldenzellen können einzelne Zellen oder eine Zellengruppe sein, deren Nachbarn einen höheren Höhenwert haben als die zu verarbeitende Zelle bzw. Zellengruppe. NoData-Zellen werden als Bereiche mit unbekannten Informationen betrachtet und werden bei der Verarbeitung nicht verwendet.

Dieses Werkzeug verwendet eine DEM-Oberfläche als Eingabe und erstellt ein Raster, das die Richtung und Akkumulation des Flusses für jede Zelle zeigt.

Wenn das Eingabe-Oberflächen-Raster echte Senken oder Flächen mit Mulden enthält, sollten diese mit dem Datenparameter Eingabe-Raster oder Feature-Mulden-Daten angegeben werden. Wenn ein Dataset angegeben ist, werden die Zellen im Eingabe-Raster mit Daten als gültige Muldenzellen betrachtet. Wenn ein Feature-Dataset angegeben wird, werden die Features mit der gleichen Auflösung wie die Eingabe-Oberflächendaten gerastert und das resultierende Raster wird zur Angabe gültiger Muldenzellen verwendet.

Das Werkzeug bietet zwei Methoden, um die Fließrichtung anhand des Parameters Fließrichtungstyp zu bestimmen: Die D8-Methode modelliert die Fließrichtung von jeder Zelle zu ihrem steilsten abwärts gelegenen Nachbarn und ist auf eine einzige Richtung beschränkt (Jenson und Domingue, 1988). Die MFD-Methode (Multiple Flow Direction) ermöglicht eine Flusspartitionierung auf alle abwärts gelegenen Nachbarn. Dabei wird der Exponent für die Partitionierung des Flusses in Abhängigkeit von den lokalen Terrainbedingungen angepasst (Qin et al, 2007).

Wenn ein Eingabe-Akkumulations-Gewichtungs-Raster angegeben ist, wird bei der Ableitung der Akkumulation auf jede Zelle eine Gewichtung angewendet.

Berechnen von Fließrichtung und Abflussakkumulation

Im Algorithmus Kontinuierlichen Fluss ableiten gibt es zwei grundlegende Schritte des Ansatzes der kostengünstigsten Route, der auf das Fluss-Routing angewendet wird. Zunächst werden gültige Abflüsse festgelegt. Gültige Abflüsse sind Zellen, in die Wasser hinein- aber nicht herausfließen kann. Bei Abflusszellen handelt es sich standardmäßig um Zellen am Rand des Eingabe-Oberflächen-Rasters. Wenn Eingabe-Raster oder Feature-Mulden-Daten angegeben ist, werden Zellen im Eingabe-Raster oder Feature-Dataset ab dem Beginn des Algorithmus ebenfalls als gültige Abflüsse gekennzeichnet. Der zweite Schritt besteht darin, das Eingabe-Oberflächen-Raster zu durchlaufen und die Fließrichtung und die Abflussakkumulation in jeder Zelle abzuleiten, indem die Zellen in der Reihenfolge von der niedrigsten Höhe bis zur höchsten Höhe verarbeitet werden. Diese beiden Prinzipien ermöglichen eine Bewegung von der aktuellen Zelle zur nächsthöheren Zelle in Richtung der am wenigsten bergauf liegenden Nachbarzelle (Metz et al, 2011; Ehlschlaeger, 1989).

Im folgenden Schema sehen Sie die allgemeine Logik, der gefolgt wird. Sonderfälle, wie z. B. Mulden (Senken), die nicht explizit als Mulden über den Parameter Eingabe-Raster oder Mulden-Daten angegeben sind, und NoData-Zellen werden in den Abschnitten Verarbeiten von unbekannten Muldenzellen bzw. NoData-Zellen im Eingabe-Oberflächen-Raster erläutert.

Abbildung 1. Der Algorithmus der kostengünstigste Route zum Bestimmen der Flussroute und -Akkumulation, wie in Metz et al., 2011; Ehlschlaeger, 1989, beschrieben, wird dargestellt.

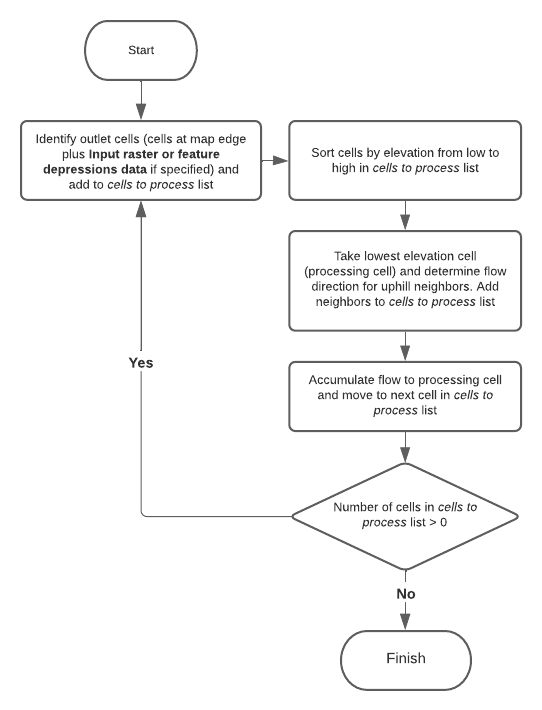
Die Logik von "Kontinuierlichen Fluss ableiten"

In diesem Abschnitt wird anhand eines Beispiel erläutert, wie das Werkzeug Kontinuierlichen Fluss ableiten Höhendaten verarbeitet und die Fließrichtung und Akkumulation auf Zellenbasis bestimmt. Das Beispiel veranschaulicht den Prozess bei Vorhandensein einer Mulde, die nicht im optionalen Parameter Eingabe-Raster oder Feature-Mulden-Daten enthalten war (siehe Abbildung 2).

Abbildung 2. Sie sehen ein Beispiel für synthetische Höhendaten mit einer Zellengröße von 1. In diesem Beispiel sehen Sie eine Mulde um den mittleren Bereich des Oberflächen-Rasters, die gelb dargestellt ist und die im Datenparameter "Eingabe-Raster oder Feature-Mulden-Daten" nicht angegeben wurde.

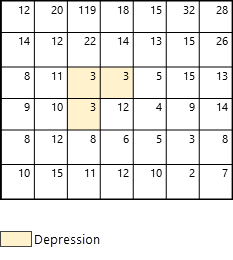
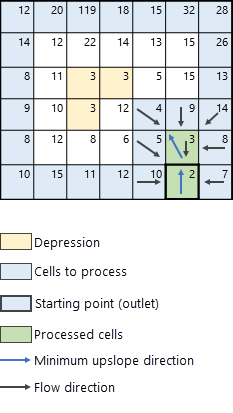
Zunächst werden die Abflüsse identifiziert. Diese entsprechen den Zellen am Kartenrand (in Abbildung 3 in blau dargestellt).

Abbildung 3. Die in Schritt 1 als potenzielle Abflüsse identifizierte Zellen werden dargestellt.

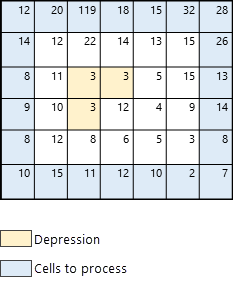
Nachdem die Abflusszellen (blaue Zellen) identifiziert wurden, sucht der Algorithmus die Zelle mit der niedrigsten Höhe, von der aus die Suche gestartet wird. In diesem Beispiel ist die niedrigste Zelle (mit Höhe 2) in Abbildung 4 durch einen dicken schwarzen Rand hervorgehoben.

Abbildung 4. In Schritt 2 wird der Startpunkt ermittelt. Dazu werden die potenziellen Abflusszellen nach Höhe sortiert, und die Zelle mit der niedrigsten Höhe wird ausgewählt und mit einem dicken schwarzen Rand hervorgehoben.

Im nächsten Schritt werden die Nachbarn der Verarbeitungszelle (in grün) ermittelt, deren Höhe größer ist als die der Verarbeitungszelle. Diese Nachbarn werden zu den möglichen Zellen hinzugefügt, die als nächstes verarbeitet werden können (siehe Abbildung 5). Die nächste Verarbeitungszelle wird bestimmt. Dazu wird der Nachbar mit der niedrigsten Höhe bergauf (in diesem Beispiel die Zelle mit dem Höhenwert 3) ermittelt, der der Richtung des minimalen Aufstiegs (blauer Pfeil in Abbildung 5) entspricht. Die Fließrichtung und die Akkumulation für die benachbarten bergauf gelegenen Zellen werden für die Verarbeitungszelle nacheinander berechnet. Die Fließrichtung wird mit der Methode bestimmt, die im Parameter Fließrichtungstyp angegeben ist. Es gibt zwei Methoden, um die Fließrichtung zu bestimmen: D8 und MFD. Eine ausführliche Erläuterung dieser beiden Methoden finden Sie im Abschnitt Methoden zur Bestimmung der Fließrichtung unten.

Abbildung 5. In Schritt 3 wurden die benachbarten Zellen der aktuellen Verarbeitungszelle identifiziert. Die blau hervorgehobenen Zellen sind Zellen, die möglicherweise als Nächstes verarbeitet werden können. Die schwarzen Pfeile entsprechen der Fließrichtung und die blauen Pfeile der Route, die für die Verarbeitung zu folgen ist.

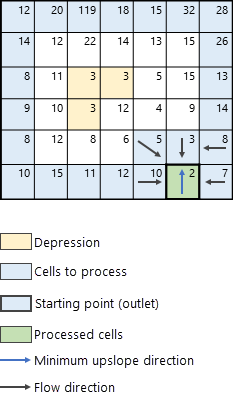
Der Algorithmus fährt auf die gleiche Weise fort und identifiziert benachbarte Zellen zur aktuellen Verarbeitungszelle, die der Richtung des minimalen Aufstiegs entspricht. Die nächste Iteration des Algorithmus ist in Abbildung 6 dargestellt.

Abbildung 6. Die nächste Iteration wird angezeigt. Wie in Abbildung 5 sind die blau hervorgehobenen Zellen die Zellen, die möglicherweise als Nächstes verarbeitet werden können. Die nächste zu verarbeitende Zelle in diesem Diagramm ist die grün dargestellte Zelle 3. Die schwarzen Pfeile entsprechen der Fließrichtung und die blauen Pfeile der Richtung der kostengünstigsten Route.

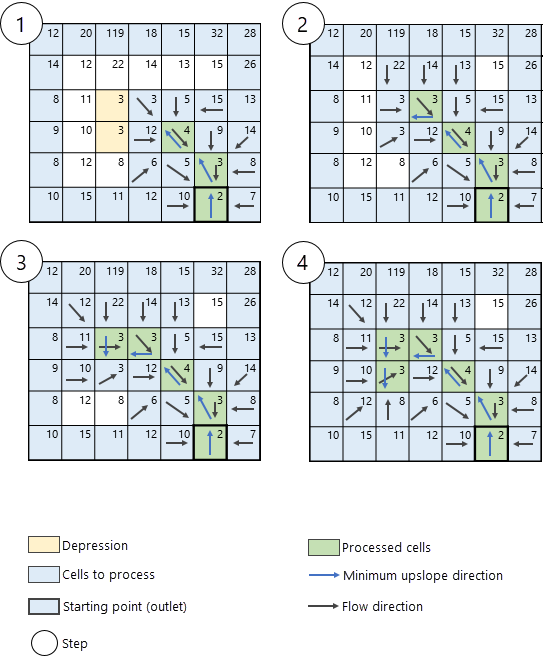
Verarbeiten von unbekannten Muldenzellen

Senkenzellen (oder Muldenzellen) können einzelne Zellen oder eine Zellengruppe sein, deren Nachbarn einen höheren Höhenwert haben als die zu verarbeitende Zelle bzw. Zellengruppe. Wenn diese Zellen nicht im Parameter Eingabe-Raster oder Feature-Mulden-Daten enthalten sind, sind sie für das Werkzeug unbekannte Muldenzellen. Wenn in diesem Szenario eine unbekannte Muldenzelle oder eine Zellengruppe gefunden wird, führt die Route über das steilste Gefälle (anstatt der Nachbarzelle mit der niedrigsten Steigung zu folgen), bis der Boden der Mulde erreicht ist, wodurch die Fließrichtung und die Akkumulation entlang des Muldenpfades festgelegt werden. Dieser Prozess ist in Abbildung 7 dargestellt.

Abbildung 7. Die Reihenfolge der Verarbeitung jeder Zelle innerhalb der Mulde wird (von links nach rechts) dargestellt. Die Fließrichtung und die Akkumulation werden beim Verarbeiten der jeweiligen Zelle innerhalb der Mulde bestimmt. Die Verarbeitungsrichtung durch die Mulde verläuft in Richtung des steilsten Gefälles, anstatt der am niedrigsten gelegenen Nachbarzelle zu folgen.

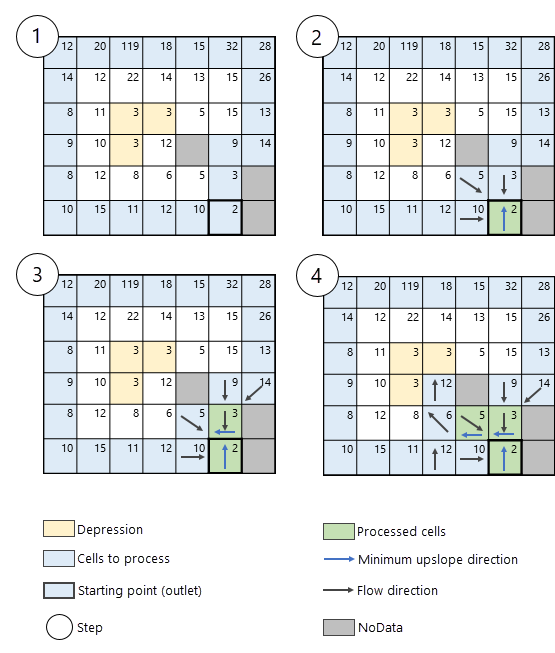
NoData-Zellen im Eingabe-Oberflächen-Raster

NoData-Zellen im Eingabe-Oberflächen-Raster sind Zellen, deren Wert nicht bekannt ist. Diese Zellen können im Oberflächen-Raster vorhanden sein und vom Algorithmus "Kontinuierlichen Fluss ableiten" erkannt werden. Wenn dies der Fall ist, werden sie nicht verarbeitet und der Algorithmus umgeht sie, wie in Abbildung 8 dargestellt.

Abbildung 8. NoData-Zellen im Eingabe-Oberflächen-Rasters werden vom Werkzeug "Kontinuierlichen Fluss ableiten" ignoriert. Äußere NoData-Zellen verschieben die Grenze des Eingabe-Oberflächen-Rasters zu den Nachbarn mit gültigen Datenwerten. Der restlichen Berechnungen zum Bestimmen der Fließrichtung und der Akkumulation bleibt gleich.

Methoden zur Bestimmung der Fließrichtung

Bei der D8-Methode wird die Fließrichtung durch die Richtung des steilsten Abgangs oder maximalen Abfalls von jeder Zelle bestimmt (Jenson und Domingue, 1988). Dieser Wert wird wie folgt berechnet:

maximum_drop = change_in_z-value/distance

Die Entfernung zwischen Zellenmittelpunkten wird berechnet. Bei über Ecken benachbarten Zellen überprüft der Algorithmus, ob der maximale Abfall in Richtung der aktuellen Verarbeitungszelle maximal ist; andernfalls wird die Fließrichtung in Richtung der Zelle mit dem maximalen Abfall der jeweiligen über Ecken benachbarten Zellen festgelegt. Wenn eine Zelle in mehrere Richtungen die gleiche Änderung im Z-Wert aufweist, ist die D8-Fließrichtung uneindeutig, und der Wert ist die Summe der möglichen Richtungen.

Sobald die Richtung des steilsten Abfalls gefunden ist, wird die Ausgabe-Zelle mit dem Wert, der diese Richtung darstellt, codiert.

Bei der MFD-Methode wird die Fließrichtung über alle niedrigeren Nachbarn hinweg partitioniert (Qin et al., 2007). Die Fließmenge, die die einzelnen niedrigeren Nachbarn erhalten, wird als Funktion des maximalen Neigungsgradienten geschätzt, die lokale Terrainbedingungen berücksichtigt. Der Ausdruck für die Schätzung der MFD lautet wie folgt:

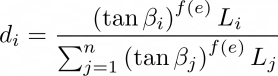
Wobei gilt:

• d_i = Teil des Abflusses aus jeder Zelle, der in die Zelle i fließt
• f (e) = Exponent, der sich an die lokalen Terrainbedingungen anpasst und angegeben wird durch

  

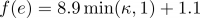
• β = Neigungswinkel (in Radiant)
• n = Anzahl der Zellen, die in die Zelle i fließen
• L_i, L_j = Angepasster Faktor zur Berücksichtigung der Entfernung zwischen der Verarbeitungszelle und den orthogonalen und diagonalen Zellen
• κ = Maximaler Abfall über Zellen hinweg, die in Zelle i fließen

Sobald Fließrichtung und Akkumulation sowie die Richtung der kostengünstigsten Route bestimmt wurden, wird die Verarbeitungszelle als verarbeitet markiert und die nächste Zelle in der Warteschlange wird analysiert. Der Algorithmus fährt auf diese Weise fort, bis alle Zellen im Eingabe-Oberflächen-Raster verarbeitet wurden. Dies bedeutet, dass die Fließrichtung und die Akkumulation für alle Zellen bestimmt wurden.

Referenzen

Ehlschlaeger, C. R. 1989. "Using the AT Search Algorithm to Develop Hydrologic Models from Digital Elevation Data." International Geographic Information Systems (IGIS) Symposium 89: 275-281.

Jenson, S. K. und Domingue, J. O. 1988. "Extracting Topographic Structure from Digital Elevation Data for Geographic Information System Analysis." Photogrammetric Engineering and Remote Sensing 54 (11): 1593–1600.

Metz, M., Mitasova, H., und Harmon, R. S. 2011 "Efficient extraction of drainage networks from massive, radar-based elevation models with least cost path search." Hydrology and Earth System Sciences 15(2): 667-678.

Qin, C., Zhu, A. X., Pei, T., Li, B., Zhou, C., und Yang, L. 2007. "An adaptive approach to selecting a flow partition exponent for a multiple flow direction algorithm." International Journal of Geographical Information Science 21(4): 443-458.