Räumliche Daten weisen häufig eine räumliche Autokorrelation auf, bei der nahe gelegene Beobachtungen ähnliche Werte aufweisen. Wenn dies in Regressionsmodellen nicht berücksichtigt wird, kann dies zu verzerrten Schätzungen und falschen Schlussfolgerungen führen.
Mit dem Werkzeug Automatische räumliche Regression kann dem begegnet werden, indem ein räumliches Regressionsmodell angepasst wird, bei dem die räumliche Abhängigkeit ausdrücklich berücksichtigt wird. Mit dem Werkzeug kann entweder eine herkömmliche Regression nach der Methode der kleinsten Quadrate oder eines der folgenden globalen räumlichen Regressionsmodelle ausgeführt werden: das räumliche Verzögerungsmodell, das räumliche Fehlermodell oder das räumlich autoregressive kombinierte Modell. Sie können angeben, welches Modell vom Werkzeug verwendet werden soll, oder das Werkzeug kann das am besten geeignete Modell ermitteln, indem es für die abhängigen und erklärenden Variablen verschiedene Diagnosetests durchführt.
Bei diesen Regressionsmodellen geht es darum, bei räumlicher Abhängigkeit aus Regressionsmodellen belastbare Rückschlüsse zu ermöglichen. Mit räumlichen Regressionsmodellen können Sie zuverlässigere Schätzungen vornehmen und die Auswirkungen des Raums in Ihren Modellen abschätzen.
Potenzielle Anwendungsbereiche
Es gibt zwei Möglichkeiten, das Werkzeug Automatische räumliche Regression so zu verwenden, dass die räumliche Abhängigkeit in Modellen berücksichtigt wird.
Zum einen ist das räumliche Verzögerungsmodell für die Analyse von räumlichen Übertragungseffekten wie den folgenden nützlich:
- Gesundheitswesen und Epidemiologie: Bewertung der Verbreitung von Krankheiten oder Viren unter Berücksichtigung der räumlichen Abhängigkeit.
- Kriminologie: Erkenntnisse über Kriminalitätscluster und die geographische Streuung von Straftaten unter Berücksichtigung von Nachbarschaftseffekten.
Zum anderen kann das räumliche Fehlermodell unverzerrte Modellschätzungen liefern, wenn wie im Folgenden die räumliche Abhängigkeit der erklärenden Variablen berücksichtigt wird:
- Sozioökonomische Analyse: Bewertung des Bildungsstands bei gleichzeitiger Kontrolle räumlich korrelierter Faktoren in den erklärenden Variablen.
- Immobilienpreise: Kontrolle für räumliche Faktoren, zu denen keine Messungen vorliegen und die sich auf die Immobilienwerte auswirken. Dadurch sind bessere Einblicke in die wichtigsten Modellvariablen möglich.
Modelltypen
Mit dem Werkzeug Automatische räumliche Regression können drei mögliche räumliche Regressionsmodelle geschätzt werden, bei denen die räumliche Abhängigkeit jeweils auf unterschiedliche Weise berücksichtigt wird. Regression der kleinsten Quadrate (Ordinary Least Squares, OLS) wird durchgeführt, wenn auf der Grundlage verschiedener Diagnosen keines der drei räumlichen Regressionsmodelle für geeignet befunden wird.
Räumliches Fehlermodell
Das räumliche Fehlermodell (Spatial Error Model, SEM) eignet sich für Situationen, in denen eine räumliche Autokorrelation in den Residuen eines Regressionsmodells besteht. Beim SEM gilt die räumliche Abhängigkeit als Störparameter. Ein Störparameter ist ein Parameter, der berücksichtigt werden muss, um sicherzustellen, dass die richtigen Schlussfolgerungen gezogen werden. Das SEM wird durch die folgende Formel definiert:

Sie ähnelt der Formel für die Regression der kleinsten Quadrate, bei der eine abhängige Variable (y) durch eine Reihe von erklärenden Variablen (x) und Koeffizienten (β) vorhergesagt wird. Der Residuenterm (u) wird jedoch durch eine andere Regressionsgleichung modelliert. Bei dieser zweiten Regression wird das Residuum mithilfe eines räumlich autoregressiven Parameters λ (Lambda) und einer räumlichen Gewichtungsmatrix (W) sowie einem eigenen Residuenterm (ε) vorhergesagt. Der Lambda-Parameter gibt an, wie stark die räumliche Abhängigkeit im Fehlerterm ist, und misst, wie stark der Fehlerterm einer Position die Fehlerterme seiner Nachbarn beeinflusst.
Beim SEM wird die räumliche Autokorrelation aus den einzelnen Variablen im Modell herausgefiltert und eine Regression für die räumlich gefilterten Variablen durchgeführt. Daher werden die Koeffizientenschätzungen nicht so stark durch die räumliche Autokorrelation der einzelnen Variablen beeinflusst.
Räumliches Verzögerungsmodell
Im Gegensatz zum SEM, bei dem die räumliche Abhängigkeit als Störparameter gilt, wird beim räumlichen Verzögerungsmodell (Spatial Lag Model, SLM) die räumliche Abhängigkeit als erklärende Variable berücksichtigt. Das räumliche Verzögerungsmodell wird verwendet, wenn die abhängige Variable eine hohe räumliche Autokorrelation aufweist und räumliche Übertragungseffekte zeigt (dass also Veränderungen in einem Gebiet Veränderungen in benachbarten Gebieten hervorrufen). Das SLM wird durch die folgende Gleichung definiert:
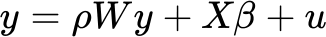
Die abhängige Variable wird durch die erklärenden Variablen sowie die eigene räumliche Verzögerung (Wy) vorhergesagt. Mit dem räumlichen autoregressiven Parameter ρ (Rho) wird gemessen, wie stark der Einfluss der Nachbarn einer Position auf den Wert der abhängigen Variable (y) ist. Größere geschätzte Werte des Parameters ρ lassen auf einen Diffusionsprozess schließen, bei dem die Werte an einer Position die Werte an benachbarten Positionen beeinflussen. Die Nachbarn wiederum können sich auf die ursprüngliche Position auswirken, was zu einer Rückkopplungsschleife führt.
Räumlich autoregressives kombiniertes Modell
Das räumlich autoregressive kombinierte Modell (Spatial Autoregressive Combined Model, SAC) enthält die räumlich autoregressiven Parameter λ und ρ aus dem räumlichen Fehlermodell bzw. aus dem räumlichen Verzögerungsmodell.

In diesem Fall wird die räumliche Abhängigkeit des Fehlerterms sowie der räumlichen Verzögerung der abhängigen Variable modelliert. Mit dem SAC-Modell können räumliche Übertragungseffekte in der abhängigen Variable ermittelt und gleichzeitig die räumliche Abhängigkeit im Fehlerterm berücksichtigt werden.
Wahl eines geeigneten Modells
Standardmäßig wählt das Werkzeug das am besten geeignete Modell anhand verschiedener statistischer Tests aus, die als Lagrange-Multiplikator-Test (LM) bezeichnet werden (auch Rao Score genannt). Dabei erfolgt die Auswahl hauptsächlich anhand des von Anselin und Rey (2014) beschriebenen Workflows.
Im folgenden Flussdiagramm sind die Entscheidungskriterien für die Auswahl des Modells dargestellt:
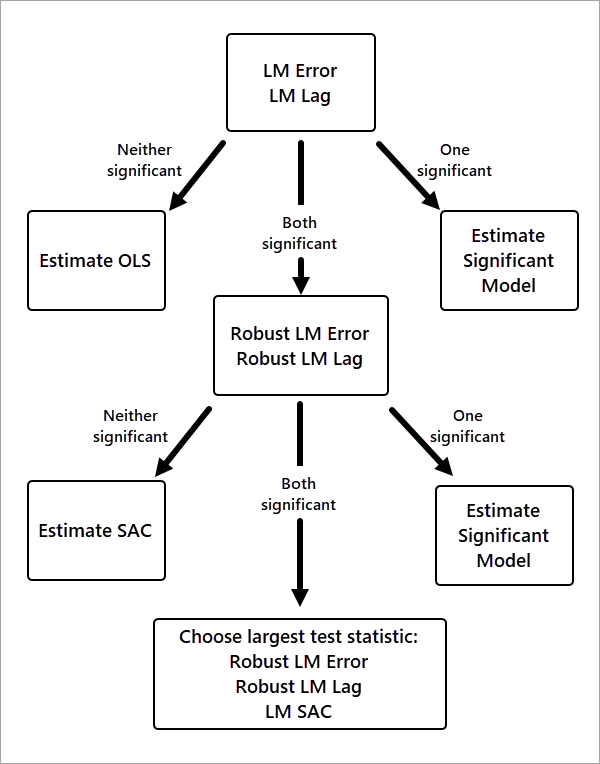
Zunächst wird der LM-Test für das räumliche Verzögerungsmodell (LM-Verzögerung) und für das räumliche Fehlermodell (LM-Fehler) durchgeführt. Wenn keiner der Tests statistisch signifikant ist (p-Wert größer als 0,05), ist kein räumliches Modell erforderlich, und es wird ein OLS-Modell gewählt. Wenn nur ein Test signifikant ist, wird das entsprechende Modell gewählt.
Wenn der Test für LM-Verzögerung und der Test für LM-Fehler signifikant sind, werden die jeweiligen robusten Entsprechungen durchgeführt. Hierbei handelt es sich um den Test für robuste LM-Verzögerung und den Test für robuste LM-Fehler. Beide Tests sind etwas strengere Testformen. Wenn nur ein Test signifikant ist, wird das entsprechende Modell gewählt.
Wenn beide robuste Tests signifikant sind, wird ein LM-Test für das SAC-Modell durchgeführt. Wenn alle drei Tests signifikant sind, wird das Modell mit dem höchsten Teststatistikwert gewählt.
In dem seltenen Fall, dass sowohl der Test für LM-Verzögerung als auch der Test für LM-Fehler signifikant sind, aber keiner der Tests für die robusten Entsprechungen, wird das SAC-Modell gewählt.
Dabei ist zu beachten, dass die LM-Tests einen datengesteuerten Ansatz zur Wahl eines Modells darstellen. Sie sind keine Garantie für ein gutes Modell oder die richtige Wahl. Betrachten Sie die Diagnosen und berücksichtigen Sie die theoretischen Annahmen für das Modell.
Werkzeugausgaben
Die primäre Ausgabe des Werkzeugs besteht aus verschiedenen Tabellen in den Geoverarbeitungsmeldungen sowie aus einer Ausgabe-Feature-Class und einem Diagramm, das die Residuen des Modells visualisiert.
Ausgabe-Features
Die Ausgabe-Feature-Class des Werkzeugs enthält Felder für die abhängige Variable, die erklärenden Variablen, den vorhergesagten Wert der abhängigen Variable, das Residuum und das standardisierte Residuum, die räumliche Verzögerung des Residuums und die Anzahl der Nachbarn jedes Features.
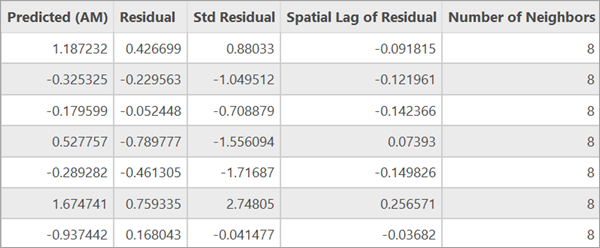
Wenn der Layer einer Karte hinzugefügt wird, werden die Features nach deren standardisierten Residuen geschummert. Die Visualisierung der standardisierten Residuen kann bei der Erkennung von Mustern der Cluster-Bildung im Fehlerterm helfen.

Die Residuen werden in einem dunkelvioletten bis dunkelgrünen Farbton symbolisiert. Grün symbolisierte Positionen weisen ein positives Residuum auf, was bedeutet, dass der Wert vom Modell zu hoch geschätzt wurde. Entsprechend weisen Positionen mit einem violetten Farbton ein negatives standardisiertes Residuum auf. Negative Residuen weisen auf eine Position hin, deren Wert zu niedrig geschätzt wurde.
Morans Scatterplot der Residuen
Der Ausgabe-Layer enthält ein Scatterplotdiagramm, in dem die Residuen entsprechend ihrer räumlichen Verzögerung dargestellt sind. Auf der X-Achse wird das standardisierte Residuum dargestellt, auf der Y-Achse die räumliche Verzögerung des standardisierten Residuums. Diese Art von Diagramm wird als Morans Scatterplot bezeichnet.
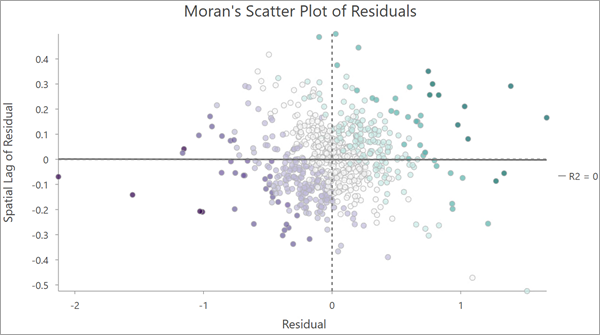
Das Diagramm kann in vier Quadranten um 0 auf der X- und Y-Achse aufgeteilt werden. Die Werte im oberen rechten und unteren linken Quadranten weisen eine positive räumliche Autokorrelation auf. Hierbei handelt es sich um Positionen, die ähnliche Werte wie die jeweiligen Nachbarn aufweisen: positive bzw. negative Werte. Die Quadranten oben links und unten rechts sind Positionen, die eine negative räumliche Autokorrelation aufweisen. Hierbei handelt es sich um Positionen, bei denen hohe Werte von niedrigen Werten umgeben sind (und umgekehrt).
Wenn die Residuen gleichmäßig über die vier Quadranten verteilt sind, deutet dies darauf hin, dass keine erkennbare räumliche Autokorrelation vorhanden ist. Diese Art von Muster ist zu erwarten, wenn das Regressionsmodell gut funktioniert und der Großteil der räumlichen Autokorrelation berücksichtigt wurde.
Geoverarbeitungsmeldungen
Das Werkzeug stellt in den Geoverarbeitungsmeldungen eine Reihe von Tabellen bereit, die Aufschluss darüber geben, wie die einzelnen Modelle geschätzt wurden:
- Zusammenfassung für Nachbarschaft und räumliche Gewichtung
- LM-Testergebnisse
- Zusammenfassung der Modellergebnisse
- Modelldiagnose
In manchen Fällen werden zudem die folgenden Meldungstabellen angezeigt:
- Zusammenfassung der Effekte des Koeffizienten
- Bericht zu lagegleichem Punkt
Die einzelnen Tabellen werden in den folgenden Abschnitten beschrieben.
Zusammenfassung für Nachbarschaft und räumliche Gewichtung
Bei den SEM-, SLM- und SAC-Modellen ist eine räumliche Gewichtungsmatrix erforderlich, die die Modellergebnisse stark beeinflussen kann. Die Tabelle "Zusammenfassung für Nachbarschaft und räumliche Gewichtung" gibt Aufschluss über die räumliche Gewichtungsmatrix, die zur Anpassung des Modells verwendet wurde. Sie enthält Informationen zum Nachbarschaftstyp, zum Gewichtungsschema, zur räumlichen Konnektivität, zur durchschnittlichen Nachbarschaftsgröße sowie zur kleinsten und größten Nachbarschaft.

Hinweis: Wenn die räumliche Gewichtungsmatrix eine zu starke Konnektivität aufweist, wird vom Werkzeug kein Modell geschätzt. Der Prozentsatz der räumlichen Konnektivität entspricht in etwa der durchschnittlichen Anzahl der Nachbarn für die einzelnen Features, ausgedrückt in Prozent der Gesamtzahl der Features. Bei 500 Features und einer räumlichen Konnektivität von 0,1 hat beispielsweise jedes Feature im Durchschnitt etwa 50 Nachbarn. Wenn die räumliche Gewichtungsmatrix eine Konnektivität von 30 Prozent oder mehr aufweist, werden die Modellergebnisse verzerrt (Smith, 2009). In diesem Fall gibt das Werkzeug einen Fehler zurück.
LM-Testergebnisse
In der Tabelle "LM-Testergebnisse" werden die Lagrange-Multiplikator-Diagnosen für die einzelnen Tests aufgeführt. Zudem ist in der Tabelle der Modelltyp angegeben, der anhand des Flussdiagramms im Abschnitt Wahl eines geeigneten Modells ausgewählt wurde.

Bericht zu lagegleichem Punkt
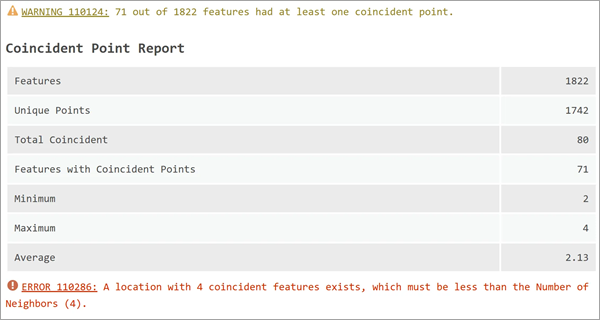
Lagegleiche Punkte (Punkte mit denselben Koordinaten) können bei der räumlichen Regression verschiedene Probleme verursachen. So können beispielsweise Gewichtungen entstehen, die für alle Nachbarn null sind. Wenn in den Eingabe-Features lagegleiche Punkte vorhanden sind, wird ein Bericht zu den lagegleichen Punkten mit folgenden Informationen angezeigt: Features gesamt, Gesamtzahl der eindeutigen Positionen und die minimale, maximale und durchschnittliche Anzahl der lagegleichen Punkte für alle Features. Zudem werden möglicherweise Warnungen und Fehler angezeigt, die durch die lagegleichen Punkte verursacht werden.
Modelldiagnose
In der Tabelle "Modelldiagnose" werden wichtige Diagnosen angezeigt, z. B. zur abhängigen Variable, zur Anzahl der Features, zu den Freiheitsgraden sowie zum verwendeten Modell.
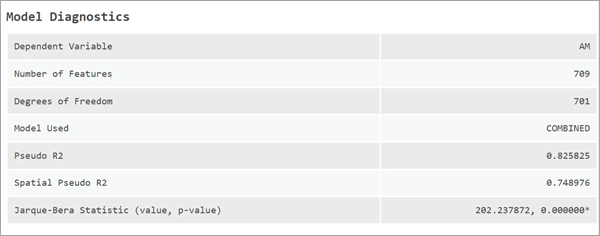
Bei der Schätzung eines OLS-Modells wird der Wert für "Adjusted R-Squared" in der Tabelle angezeigt. Für alle räumlichen Modelle wird dagegen der Wert für "Pseudo-R-Squared" angezeigt. Auch für das SLM und das SAC-Modell wird ein räumlicher Wert für "Pseudo-R-Squared" angezeigt. Diese Werte werden nachfolgend beschrieben.
Zusätzlich wird auch die Jarque-Bera-Statistik angegeben. Wenn die Statistik signifikant ist, bedeutet dies, dass die Residuen des Modells nicht normalverteilt sind. Obwohl die Modelle mit Methoden geschätzt werden, die gegenüber einer Nicht-Normalverteilung unempfindlich sind, kann der Test auf fehlende Angaben oder das Vorhandensein von Ausreißern im Modell hinweisen.
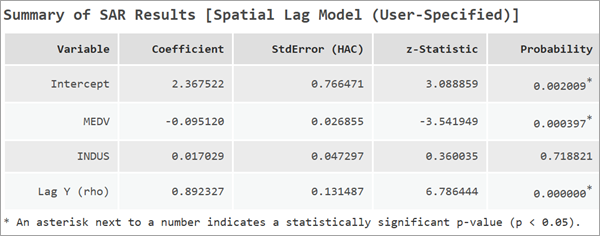
Interpretieren der Ergebnisse des räumlichen Verzögerungsmodells
Das räumliche Verzögerungsmodell enthält einen zusätzlichen Koeffizienten, der als Verzögerung Y (Rho) bezeichnet wird. Hierbei handelt es sich um die räumliche Verzögerung der abhängigen Variable. Der Koeffizient dieser Variable gibt die Stärke und Richtung der räumlichen Abhängigkeit der abhängigen Variable an. Der Wert von Rho muss zwischen –1 und 1 liegen. Größere Werte für Verzögerung Y deuten auf eine starke räumliche Rückkopplung hin.

Hinweis: Eine Veränderung einer erklärenden Variable an einer Position kann den Wert der abhängigen Variable an einer anderen Position beeinflussen, was als räumliche Übertragung bezeichnet wird. Ist eine räumliche Übertragung vorhanden, müssen die Regressionskoeffizienten zusammen mit dem räumlichen Übertragungseffekt interpretiert werden.
Auswirkungen und Koeffizienteneffekte
Neben den Regressionskoeffizienten wird zudem eine Kennzahl mit der Bezeichnung "Auswirkungen" angegeben. Mithilfe von "Auswirkungen" kann für alle erklärenden Variablen der Effekt von räumlichen Übertragungen angegeben werden. Dabei wird zwischen direkten und indirekten Auswirkungen und Auswirkungen insgesamt unterschieden. Zur Berechnung der Auswirkungen gibt es verschiedene Ansätze, und dieses Werkzeug liefert einfache Auswirkungen. Die direkten und indirekten Auswirkungen und die Auswirkungen insgesamt werden in der Meldungstabelle "Zusammenfassung der Effekte des Koeffizienten" angezeigt.
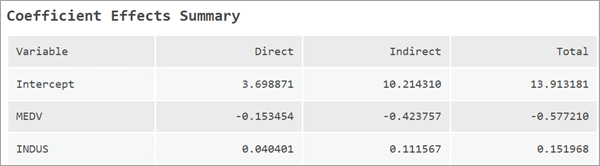
Die direkte Auswirkung gibt an, wie stark sich die Änderung einer erklärenden Variable um eine Einheit auf den Wert der abhängigen Variable an der jeweiligen Position auswirkt. Bei einfachen Auswirkungen entspricht dieser Wert dem Beta-Koeffizienten.

Die indirekte Auswirkung gibt dagegen an, wie stark sich die Änderung einer Variablen um eine Einheit auf die abhängige Variable an den benachbarten Positionen auswirkt. Es ist jedoch zu beachten, dass der Wert von Auswirkungen stark von der räumlichen Gewichtungsmatrix beeinflusst wird.
Standardfehler
Das räumliche Verzögerungsmodell gibt robuste Standardfehler an. Nach der Anpassung eines räumlichen Verzögerungsmodells verbleibt jedoch möglicherweise ein Großteil der Autokorrelation in den Residuen. Der Anselin-Kelejian-Test (AK) ist ein Diagnosetest, mit dem festgestellt werden kann, ob in den Modellresiduen eine signifikante räumliche Abhängigkeit verbleibt.
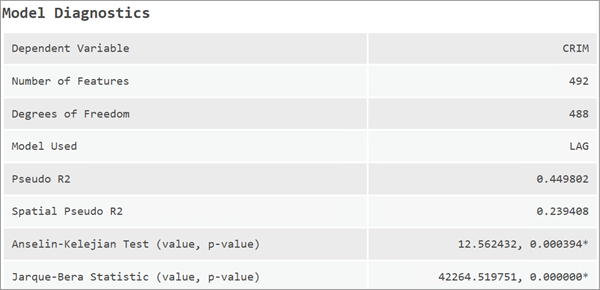
Wenn der AK-Test signifikant ist (p-Wert kleiner als 0,05), wird eine andere Kennzahl für Standardfehler, die sogenannten heteroskedastizitäts- und autokorrelationskonsistenten Standardfehler (Heteroskedastic and Autocorrelation Consistent, HAC) angegeben. Bei HAC-Standardfehlern handelt es sich um eine nichtparametrische Variante von Standardfehlern, die nützlich ist, wenn eine räumliche Autokorrelation vorliegt.
Bei HAC-Standardfehlern wird die räumliche Verteilung der Daten durch Verwendung einer separaten räumlichen Gewichtungsmatrix berücksichtigt. Die räumliche Gewichtungsmatrix wird mithilfe der Option "Nächste Nachbarn (K)" erstellt, um die Nachbarschaft der einzelnen Features mit dem in der Nachbarschaft enthaltenen fokalen Feature zu bestimmen. Die Gewichtungen der einzelnen Nachbarschaften werden unter Verwendung eines Dreieck-Kernels modelliert.
"Pseudo R-Squared" und "Spatial Pseudo R-Squared"
Da das räumliche Verzögerungsmodell die räumliche Verzögerung der abhängigen Variable als erklärende Variable enthält, können keine herkömmlichen Vorhersagemethoden für lineare Regression verwendet werden. Die Vorhersage der abhängigen Variable anhand der räumlichen Verzögerung führt zu übermäßig zuversichtlichen Schätzungen. Um dies zu vermeiden, wird eine andere Kennzahl berechnet, nämlich der Wert für "Spatial Pseudo R-Squared".
Der Wert für "Spatial Pseudo R-Squared" wird ohne die räumliche Verzögerung der abhängigen Variable berechnet. Stattdessen werden die räumliche Gewichtungsmatrix und die Schätzung von λ verwendet, um vorhergesagte Werte von Wy-hat zu erstellen, der in der Vorhersage anstelle von Wy verwendet wird.
Die vorhergesagten Werte werden dann zur Berechnung eines herkömmlichen "Pseudo R-Squared"-Wertes verwendet. Es wird empfohlen, eher den Wert für "Spatial Pseudo R-Squared" anzugeben als den Wert für "Pseudo R-Squared".
Dabei ist zu beachten, dass der Wert für "Spatial Pseudo R-Squared" eine andere Kennzahl darstellt als der Wert für "Adjusted R-Squared", der in OLS-Ergebnissen angegeben wird. Daher können die beiden nicht miteinander verglichen werden.
Interpretieren der Ergebnisse des räumlichen Fehlermodells
Beim räumlichen Fehlermodell können die Regressionskoeffizienten ähnlich wie bei der linearen Standardregression interpretiert werden. Jeder Koeffizient gibt die Veränderung der abhängigen Variable bei einer Änderung der unabhängigen Variable um eine Einheit an. Das SEM enthält jedoch noch eine weitere Komponente, das Verzögerungs-Residuum (Lambda), das für das Verständnis der räumlichen Abhängigkeit innerhalb des Modells wichtig ist. Der Koeffizient des Verzögerungs-Residuums (Lambda) liegt immer zwischen –0,99 und 0,99.

Ein positiver Lambda-Wert besagt, dass die Residuen ein räumliches Clustering aufweisen, während ein negativer Lambda-Wert besagt, dass die Residuen eine räumliche Streuung aufweisen. Größere absolute Lambda-Werte (positive oder negative) deuten zudem darauf hin, dass es räumliche Prozesse gibt, die von den erklärenden Variablen nicht erfasst werden. Durch die Einbeziehung von zusätzlichen relevanten erklärenden Variablen kann der Koeffizient auf einen moderateren Wert gesenkt werden.
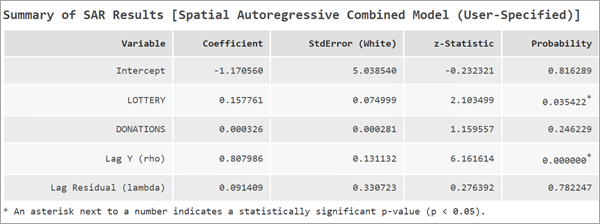
Interpretieren der Ergebnisse des räumlich autoregressiven kombinierten Modells
Wenn das SAC-Modell ausgewählt ist, werden alle für das SLM- und das SEM-Modell geltenden Abschnitte in den Meldungen angezeigt.
Referenzen
Bei der Implementierung des Werkzeugs wurden folgende Ressourcen verwendet:
- Anselin, L. und Sergio J. Rey. 2014 "Modern spatial econometrics in practice: A guide to GeoDa, GeoDaSpace and PySAL." ISBN 9780986342103.
Bivand, Roger und Gianfranco Piras. 2015. "Comparing implementations of estimation methods for spatial econometrics." Journal of Statistical Software. 63: 1-36. https://doi.org/10.18637/jss.v063.i18.
Kelejian, Harry H. und Ingmar R. Prucha. 2007. "HAC estimation in a spatial framework." Journal of Econometrics. 140, no. 1: 131-154. https://doi.org/10.1016/j.jeconom.2006.09.005.
Smith, Tony E. 2009. "Estimation Bias in Spatial Models with Strongly Connected Weight Matrices." Geographical Analysis. 41, no. 3: 307-332. https://doi.org/10.1111/j.1538-4632.2009.00758.x.