Funktionsweise von "Zeit bis zum Ereignis schätzen"

Das Werkzeug Zeit bis zum Ereignis schätzen sagt die Zeit bis zum Eintreten eines Ereignisses für eine Reihe von Beobachtungen auf der Grundlage vergangener Zeitpunkte bis zum Eintreten des Ereignisses und der spezifischen Eigenschaften der Beobachtungen voraus. Die Eingabe muss eine Mischung aus Datensätzen sein, für die das Ereignis eingetreten ist, und Datensätzen, für die das Ereignis nicht eingetreten ist. Das Werkzeug enthält erklärende Variablen und schätzt, ob diese die Zeit bis zum Ereignis verkürzen oder verlängern. Das Werkzeug sagt auch die zusätzliche Zeit bis zum Eintreten des Ereignisses für Beobachtungen voraus, bei denen das Ereignis noch nicht eingetreten ist.

This video was created with ArcGIS Pro 3.5.

Jede Beobachtung in den Eingabe-Features oder der -Tabelle muss Felder enthalten, die das Alter der Beobachtung, einen Indikator dafür, ob das Ereignis bereits eingetreten ist, und erläuternde Variablen enthalten. Diese Felder werden in den Parametern Feld "Alter", Feld "Ereignisindikator" und Erklärende Variablen bereitgestellt. Die erklärenden Variablen können kontinuierlich oder kategorial sein, und der Ereignisindikator darf nur die Werte 0 (das Ereignis ist nicht eingetreten) oder 1 (das Ereignis ist eingetreten) annehmen. Für das Feld "Alter" ist dies oft das tatsächliche Alter der Person, aber im Allgemeinen ist es die Zeitspanne, die vom ersten möglichen Zeitpunkt für das Eintreten des Ereignisses bis zum Zeitpunkt des Eintretens des Ereignisses (oder der aktuellen Zeit, wenn das Ereignis nicht eingetreten ist) reicht. Um beispielsweise die Lebensdauer von Bäumen zu schätzen, sollten die Werte im Feld "Alter" das aktuelle Alter des Baumes angeben, wenn er noch lebt, oder das Alter des Baumes, als er gestorben ist. Für die Schätzung der Zeit bis zur erneuten Festnahme sollten jedoch die Feldwerte die Zeitspanne zwischen der Entlassung der Person aus der Haft (dem ersten Zeitpunkt, an dem eine erneute Festnahme erfolgen könnte) und dem Zeitpunkt der erneuten Festnahme (oder dem aktuellen Datum, wenn die Person nicht erneut festgenommen wurde) sein. Die Einheit für das Alter (Stunden, Tage, Jahre usw.) muss nicht angegeben, aber alle Ergebnisse müssen in dieser Zeiteinheit ausgedrückt werden.

Das Werkzeug erzeugt eine Vielzahl von Ausgaben, sowohl numerisch als auch graphisch. Diese dienen dazu, die Auswirkungen der erklärenden Variablen auf die Zeit bis zum Eintreten des Ereignisses zu verstehen, das Eintreten des Ereignisses vorherzusagen und die Genauigkeit und Zuverlässigkeit des Modells zu bewerten.

Potenzielle Anwendungsbereiche

Modelle vom Typ "Zeit bis zum Ereignis" sind in einer Vielzahl von Bereichen nützlich, in denen das Ziel darin besteht, abzuschätzen, wie lange es dauert, bis ein Ereignis eintritt, und welche Faktoren den zeitlichen Ablauf beeinflussen. Nachfolgend finden Sie einige potenzielle Anwendungsbereiche des Werkzeugs:

• Instandhaltung der Infrastruktur: Abschätzen der Zeit, bis eine Rohrleitung undicht wird, eine Brücke größere Reparaturen benötigt oder ein Transformator ausfällt. Zu den erklärenden Variablen könnten die Materialart (kategorial), die Belastung durch extremes Wetter (kategorial) und die Verkehrsbelastung (kontinuierlich) gehören.
• Forstwirtschaft: Modellieren der Zeit, bis ein Baum einen bestimmten Durchmesser erreicht hat, gefällt werden muss oder einer Krankheit erliegt. Zu den erklärenden Variablen könnten der anfängliche Stammdurchmesser (kontinuierlich), die Baumart (kategorial), die Bodenqualität (kontinuierlich) und die konkurrierende Wirkung benachbarter Bäume (kategorial) gehören.
• Kreditausfall: Vorhersage der Zeit bis zum Ausfall eines Kreditnehmers bei einem Darlehen. Zu den erklärenden Variablen könnten der Darlehensbetrag (kontinuierlich), die Kreditwürdigkeit (kontinuierlich), die Beschäftigungsart (kategorial) und das Zahlungsverhalten in der Vergangenheit (kategorial) gehören.
• Kundenbindung: Abschätzen, wann ein Kunde ein Abonnement kündigt oder den Anbieter wechselt. Die erklärenden Variablen könnten den monatlichen Rechnungsbetrag (kontinuierlich), die Vertragsdauer (kategorial), die Anzahl der Beschwerden beim Kundendienst (kontinuierlich) und die erhaltenen Aktionsrabatte (kategorial) umfassen.
• Fertigung: Vorhersagen, wann eine Maschine gewartet oder ausgetauscht werden muss. Die erklärenden Variablen könnten die Betriebsstunden (kontinuierlich), das Modell der Maschine (kategorial) und die Temperatur in der Fabrik (kontinuierlich) umfassen.

Ereigniszeitanalyse und Überlebensanalyse

Die Ereigniszeitanalyse ist ein Teilgebiet der Statistik, bei der geschätzt, erklärt und vorhergesagt wird, wann ein Ereignis für eine festgelegte Anzahl von Beobachtungen eintreten wird, wobei davon ausgegangen wird, dass das Ereignis bei jeder Beobachtung nach einer gewissen Zeit eintritt. Die Ereigniszeitanalyse wird am häufigsten in der medizinischen Forschung eingesetzt, wo sie in der Regel als Überlebensanalyse bezeichnet wird, da das modellierte Ereignis der Tod einer Person ist. Aus diesem Grund sind viele der Begriffe und Konzepte in der Ereigniszeitanalyse aus der Überlebensanalyse entlehnt. Zum Beispiel wird die Zeitspanne, bis das Ereignis nach der Beobachtung eintritt, als seine Lebensdauer bezeichnet, und die Kurve, mit der die Zeit bis zum Ereignis abgeschätzt wird, wird als seine Überlebenskurve bezeichnet. Bei Anwendungen wie der Vorhersage des Baumsterbens oder des Ausfalls von Infrastruktur passt die Terminologie natürlich, aber sie ist weniger klar, wenn es beispielsweise um die Abschätzung der Zeit bis zu einer erneuten Festnahme geht. In diesem Fall wäre die Überlebenszeit einer Person die Zeitspanne bis zur erneuten Festnahme. Ähnlich verhält es sich, wenn man über die Wahrscheinlichkeit spricht, dass eine Person mindestens fünf Jahre lang nicht erneut festgenommen wird. In diesem Fall würde man von der Wahrscheinlichkeit sprechen, dass die Überlebenszeit fünf Jahre überschreitet. In diesem Thema wird je nach Kontext zwischen der Diskussion von der Ereigniszeit und der Überlebenszeit gewechselt, aber sie sollten als dasselbe verstanden werden.

Ein weiterer Unterschied zwischen der Ereigniszeitanalyse und der Überlebensanalyse besteht darin, dass sich die Überlebensanalyse in erster Linie auf die Abschätzung der Wirkung einer Behandlung (in der Regel eines Medikaments, das sich in medizinischen Studien befindet) auf die Überlebenszeit konzentriert und weniger auf die Vorhersage der Überlebenszeiten einzelner Menschen. Grundsätzlich geht es um die Frage, ob das Medikament die Überlebenszeit verlängert, und nicht darum, wie lange ein bestimmter Mensch leben wird. Die Ereigniszeitanalyse konzentriert sich jedoch mehr auf die Vorhersage, wann das Ereignis für einzelne Beobachtungen eintreten wird, und weniger auf die Schätzung, ob die erklärenden Variablen die Überlebenszeit verlängern oder verkürzen. Zwar können alle Modelle der Überlebensanalyse für Ereigniszeitanalysen verwendet werden (und umgekehrt), doch sind einige Modelle besser für das eine oder das andere geeignet. Dieses Werkzeug verwendet insbesondere ein parametrisches Modell der beschleunigten Ausfallzeit, das sich besser für die Vorhersage der Zeit bis zum Ereignis eignet, während medizinische Studien in der Regel ein nichtparametrisches Cox-Modell der proportionalen Risiken verwenden, das sich besser für die Abschätzung der Wirkung medizinischer Behandlungen eignet.

Überlebenskurven

Bei der Schätzung der Zeit bis zum Eintritt des Ereignisses wird für jede Beobachtung eine Überlebenskurve erstellt, die von den erklärenden Variablen abhängt. Die Überlebenskurve ist eine Funktion, die die Wahrscheinlichkeit darstellt, dass die Überlebenszeit eine bestimmte Zeitspanne überschreitet (mit anderen Worten, die Wahrscheinlichkeit, dass die Person nach einer bestimmten Zeit noch am Leben ist). Die Überlebenskurve beginnt immer bei 1 und sinkt mit der Zeit auf 0. Die folgende Überlebenskurve ähnelt beispielsweise der Überlebenskurve von Menschen:

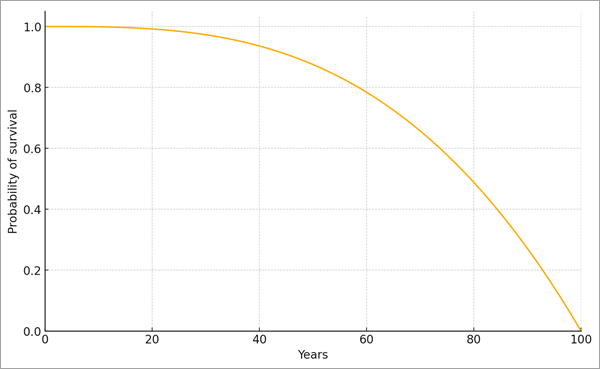
In dieser Kurve überlebt die überwiegende Mehrheit der Menschen das 20. Lebensjahr, bevor die Kurve anfängt, sich nach unten zu neigen. Mit 60 Jahren sind noch knapp 80 Prozent der Menschen am Leben. Die Median-Überlebenszeit (0,5 auf der Y-Achse) beträgt etwa 80 Jahre, und nach 100 Jahren sind fast keine Menschen mehr am Leben.

Aus der Überlebenskurve können beliebige Quantile der Zeit bis zum Ereignis berechnet werden. Zum Beispiel ist das 5. Perzentil der Zeit bis zum Ereignis der Wert der X-Achse, wenn die Kurve 0,95 beträgt (wenn eine Wahrscheinlichkeit von 95 Prozent besteht, dass das Ereignis noch nicht eingetreten ist), und das 75. Perzentil ist, wenn die Kurve 0,25 beträgt. Diese Quantile können dazu verwendet werden, Konfidenzintervalle zu erstellen. Beispielsweise ist die Zeit zwischen dem 5. und 95. Quantil ein 90-prozentiges Konfidenzintervall für die Zeit bis zum Ereignis. Während beliebige Quantile berechnet werden können, werden Überlebenskurven häufig durch die mittlere Überlebenszeit zusammengefasst (dies ist der Wert der X-Achse, wenn die Überlebenskurve gleich 0,5 ist).

Modell für beschleunigte Ausfallzeiten

Das statistische Modell, das zur Schätzung der Zeit bis zum Eintreten des Ereignisses verwendet wird, wird als Modell für beschleunigte Ausfallzeiten (Accelerated Failure Time, AFT) bezeichnet. Bei Modellen für beschleunigte Ausfallzeiten wird davon ausgegangen, dass jede Beobachtung in Abhängigkeit von ihren individuellen erklärenden Variablen unterschiedlich schnell altert. Zum Beispiel wird oft gesagt (obwohl es nicht wahr ist), dass Hunde siebenmal so schnell altern wie Menschen, dass ein dreijähriger Hund sich an einem Punkt in seinem Leben befindet, der dem eines 21-jährigen Menschen entspricht. Ein weiteres Beispiel: Bei zwei Brücken könnte davon ausgegangen werden, dass sie sich unterschiedlich schnell abnutzen. Eine Brücke kann 30 Jahre alt sein und als gleichwertig abgenutzt gelten wie eine andere Brücke, die erst 10 Jahre alt ist, je nach den Eigenschaften der Brücken, wie Baumaterial, Verkehrsaufkommen und Umweltbedingungen.

In Modellen für beschleunigte Ausfallzeiten bewirken die erklärenden Variablen eine Beschleunigung oder Verlangsamung der Zeit bis zum Ereignis, was als Zeitverhältnis ausgedrückt wird. Das Zeitverhältnis zwischen zwei Beobachtungen, A und B (jeweils mit unterschiedlichen erklärenden Variablen), ist das Verhältnis der erwarteten Lebensdauerangaben von A und B. Ein Zeitverhältnis von 1,3 bedeutet beispielsweise, dass die Lebensdauer von Beobachtung A voraussichtlich 30 Prozent länger ist als die von Beobachtung B. Gleichermaßen bedeutet ein Zeitverhältnis von 0,6, dass eine Verkürzung um 40 Prozent erwartet wird. Ein Zeitverhältnis von 1 bedeutet, dass beide Beobachtungen voraussichtlich dieselbe Lebensdauer haben. Beachten Sie, dass für das Zeitverhältnis eine Basislinie oder ein Referenzwert erforderlich ist, mit dem verglichen wird (in diesem Fall die Lebensdauer der Beobachtung B).

Der Effekt des Zeitverhältnisses besteht darin, die Überlebenskurve horizontal zu strecken. Das folgende Bild zeigt beispielsweise vier Überlebenskurven, die die Auswirkungen von Zeitverhältnissen von 1 (blaue Kurve, mit der verglichen wird), 2 (orangefarbene Kurve), 3 (grüne Kurve) und 4 (rote Kurve) von links nach rechts darstellen. Es ist schwer zu erkennen, dass die Kurven gestreckte Versionen voneinander sind, daher ist bei der Median-Überlebenszeit eine horizontale gestrichelte Linie gezogen. Beachten Sie, dass die Median-Überlebenszeit für das Zeitverhältnis 2 doppelt so hoch ist wie die mediane Zeit für das Zeitverhältnis 1. Gleichermaßen beträgt die Median-Überlebenszeit für die Zeitverhältnisse 3 und 4 das Drei- bzw. Vierfache der mittleren Überlebenszeit für das Zeitverhältnis 1. Während die gestrichelte Linie auf dem Median liegt, bleiben diese Verhältnisse auch bei Verwendung eines anderen Wertes auf der Y-Achse erhalten.

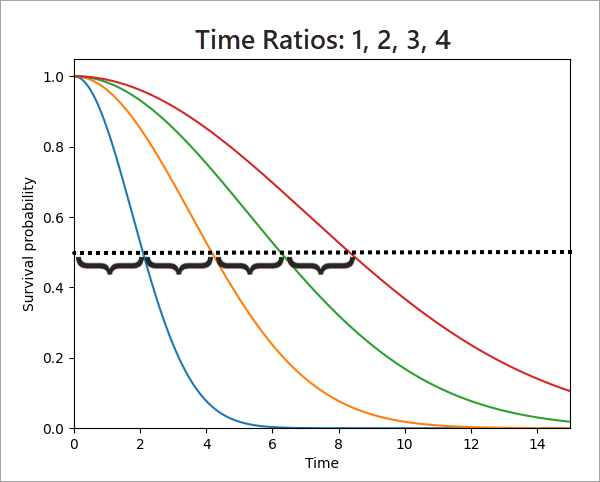
Die Verwendung der blauen Kurve ganz links als Basislinie war eine willkürliche Entscheidung. Wäre die rote Kurve ganz rechts stattdessen als die zu vergleichende Basislinie definiert worden, würden die Zeitverhältnisse 0,25, 0,5, 0,75 und 1 (von links nach rechts) betragen. Diese Zeitverhältnisse kleiner als 1 zeigen an, dass die rote Überlebenskurve die längste erwartete Überlebensdauer unter den vier Kurven aufweist.

Das Werkzeug schätzt ein Zeitverhältnis für jede erklärende Variable, testet die statistische Signifikanz des Zeitverhältnisses und zeigt das Ergebnis in den Meldungen an (weitere Informationen finden Sie im Abschnitt Geoverarbeitungsmeldungen weiter unten). Die Interpretation des Zeitverhältnisses hängt davon ab, ob die erklärende Variable kategorial oder kontinuierlich ist, da sie ihre Basislinien unterschiedlich definieren. Bei kategorialen Variablen muss eine der Kategorien als Referenzkategorie festgelegt werden, und für alle anderen Kategorien werden Zeitverhältnisse im Vergleich zur Referenzkategorie erstellt. Wenn ein kategoriales Variablenfeld beispielsweise über die Einzelwerte A, B und C verfügt und Kategorie A die Referenzkategorie ist, werden Zeitverhältnisse nur für die Kategorien B und C berechnet. Wenn das Zeitverhältnis für Kategorie B 2,2 beträgt, bedeutet dies, dass eine Beobachtung in Kategorie B schätzungsweise 2,2-mal länger lebt als eine Beobachtung in Kategorie A, vorausgesetzt, alle anderen Attribute sind gleich (oder, äquivalent dazu, dass die Überlebenskurven für Kategorie B 2,2-mal breiter sind als die Überlebenskurven für Kategorie A). Das Werkzeug verwendet die erste alphanumerisch sortierte Kategorie als Referenzkategorie. Sie können jedoch die Feldwerte reklassifizieren, um festzulegen, welche Kategorie als Referenzkategorie verwendet werden soll.

Bei kontinuierlichen Variablen ist das Zeitverhältnis die Veränderung der Lebensdauer bei einer Erhöhung der erklärenden Variablen um eine Einheit. In diesem Fall wird ein Vergleich zwischen zwei Beobachtungen durchgeführt, die sich im Wert der erklärenden Variablen um genau 1 unterscheiden (wobei alle anderen erklärenden Variablen gleich sind). Wenn beispielsweise bei der Schätzung der Lebensdauer von Bäumen der Stammdurchmesser in Metern eine erklärende Variable ist, misst das Zeitverhältnis die Zunahme (oder Abnahme) der Lebensdauer durch Erhöhung des Baumdurchmessers um 1 Meter. Wenn Bäume mit größeren Stammdurchmessern dazu neigen, länger zu leben, ist das Zeitverhältnis größer als 1, und wenn sie dazu neigen, kürzer zu leben, ist das Zeitverhältnis kleiner als 1. Da das Zeitverhältnis ein Multiplikator ist, erhöht eine Erhöhung der erklärenden Variablen um zwei Einheiten die Lebensdauer um den Wert des Zeitverhältnisses hoch zwei; eine Erhöhung der erklärenden Variablen um drei Einheiten erhöht die Lebensdauer um den Wert des Zeitverhältnisses hoch drei; und so weiter. Diese Art der Zusammensetzung des Zeitverhältnisses für kontinuierliche erklärende Variablen kann zu Modellierungsproblemen führen (weitere Informationen und Empfehlungen finden Sie im Abschnitt Empfehlungen und Beschränkungen und empfohlener Workflow weiter unten).

Schätzung des Modells für beschleunigte Ausfallzeiten

Das Modell für beschleunigte Ausfallzeiten verwendet eine Weibull-Verteilung zum Modellieren der Überlebenskurve:

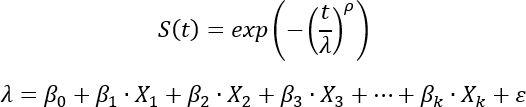
Der Skalenparameter (λ) wird als lineares Modell der erklärenden Variablen (X_i) und der geschätzten Koeffizienten (β_i) geschätzt. Es ist der Skalenparameter, der die Streckung der Überlebenskurve steuert, wie im vorherigen Abschnitt beschrieben. Intuitiv ausgedrückt wird die Überlebenskurve für eine Beobachtung durch die spezifischen Attribute dieser Beobachtung verlängert (oder verkürzt), je nachdem, ob diese Attribute im Allgemeinen mit einer längeren oder kürzeren Lebensdauer in Verbindung gebracht werden.

Der Formparameter (ρ) wird für alle Beobachtungen gleich verwendet und ermöglicht es der Überlebenskurve, innerhalb desselben Zeitraums verschiedene Formen anzunehmen. Die folgende Abbildung zeigt verschiedene Formen für Weibull-Verteilungen mit demselben Skalenparameter:

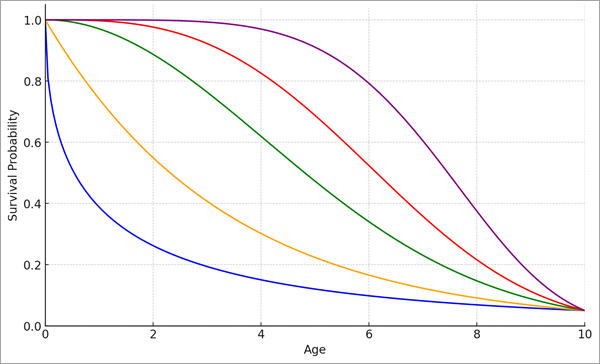
Der Formparameter wird manchmal auch als Beschleunigungsparameter bezeichnet, da er angibt, ob die Überlebenskurve beschleunigt oder verlangsamt wird. Die Beschleunigung wird anhand der Hazard-Funktion gemessen, die als Wahrscheinlichkeit definiert ist, dass das Ereignis zu einem bestimmten Zeitpunkt eintritt, unter der Annahme, dass das Ereignis zuvor noch nicht eingetreten ist. Wenn beispielsweise ältere Brücken in naher Zukunft mit größerer Wahrscheinlichkeit repariert werden müssen als jüngere Brücken, steigt die Hazard-Funktion mit der Zeit an (mit anderen Worten: Ältere Brücken sind gefährdeter als jüngere Brücken), sodass sich die Überlebenskurve mit der Zeit beschleunigt. Umgekehrt gilt: Wenn ältere Brücken in naher Zukunft weniger reparaturbedürftig sind als jüngere Brücken, sinkt die Hazard-Rate und die Überlebenskurve verlangsamt sich. Formparameterwerte über 1 weisen auf eine beschleunigte Überlebenskurve hin, Werte unter 1 auf eine verlangsamte Überlebenskurve. Das Modell kann jedoch keine variierenden Hazard-Raten schätzen, bei denen sich die Überlebenskurve zu unterschiedlichen Zeitpunkten sowohl beschleunigt als auch verlangsamt (z. B. ist die Sterblichkeitsrate bei Säuglingen höher, bei Kindern und jungen Erwachsenen niedriger und bei älteren Erwachsenen wieder höher).

Alle Koeffizienten und der Formparameter werden mithilfe der Maximum-Likelihood-Methode geschätzt und vom Werkzeug als Meldungen angezeigt.

Zensierte Beobachtungen und Vorhersagen

In den vorherigen Abschnitten wurde beschrieben, wie Überlebenskurven für jede Beobachtung geschätzt werden, unabhängig davon, ob das Ereignis für die Beobachtung bereits eingetreten ist oder nicht. Zum Beispiel kann eine Überlebenskurve für eine bereits eingestürzte Brücke erstellt werden. Im Wesentlichen zeigt diese Überlebenskurve die erwartete Lebensdauer der Brücke, wenn sie heute mit den gleichen Eigenschaften gebaut würde. Diese Informationen können zwar nützlich sein, aber noch nützlicher ist es, Überlebenskurven zu erstellen, die die zusätzliche Lebensdauer von Beobachtungen vorhersagen, bei denen das Ereignis nicht eingetreten ist (z. B. Vorhersage, wie lange eine vorhandene Brücke noch hält, bis sie repariert werden muss).

Beobachtungen, bei denen das Ereignis noch nicht eingetreten ist, werden als zensierte Beobachtungen bezeichnet, Beobachtungen, bei denen das Ereignis bereits eingetreten ist, als unzensierte Beobachtungen. Diese Terminologie erklärt sich aus dem Umstand, dass unzensierte Beobachtungen vollständige Informationen enthalten (die Überlebenszeit ist bekannt), während zensierte Beobachtungen nur Teilinformationen enthalten; die genaue Überlebenszeit ist nicht bekannt, aber es ist bekannt, dass sie eine bestimmte Zeitdauer (das aktuelle Alter der Beobachtung) überschreitet. Vergleichbar ist dies mit der Vorstellung, dass ein Dokument unzensiert oder zensiert sein kann: Demnach können alle Informationen des Dokuments verfügbar sein (ein unzensiertes Dokument) oder infolge einer Zensur zum Teil geschwärzt sein (ein zensiertes Dokument).

Bei zensierten Beobachtungen besteht das Ziel darin, eine Überlebenskurve zu erstellen, die die zusätzliche Zeit bis zum Ereignis schätzt, wenn man das aktuelle Alter berücksichtigt. Diese zusätzliche Überlebenszeitkurve kann durch Konditionierung der Zeitspanne erstellt werden, die die Person bereits überlebt hat. Mathematisch wird die zusätzliche Überlebenszeitkurve S_Add(T) berechnet als S_Add(T) = S(C+T)/S(C) für T zusätzliche Zeiteinheiten nach dem Zeitpunkt der Zensur C.

Die zusätzliche Überlebenszeitkurve kann als eine Neuskalierung der Überlebenskurve der Beobachtung nach dem Zeitpunkt der Zensur visualisiert werden. Das folgende Bild zeigt beispielsweise eine Überlebenskurve für eine Beobachtung, die zum Zeitpunkt 4 zensiert wurde. Aufgrund der erklärenden Variablen bestand eine Wahrscheinlichkeit von etwa 60 Prozent, dass die Person mindestens vier Zeiteinheiten (der Wert auf der Y-Achse zum Zeitpunkt der Zensur) leben würde. Da jedoch bekannt ist, dass die Person mindestens vier Zeiteinheiten (der Zeitpunkt der Zensur) überlebt hat, werden die Werte auf der Y-Achse neu skaliert, sodass sie wieder bei 1 beginnen (mit anderen Worten: Es besteht eine 100-prozentige Wahrscheinlichkeit, dass die Person mindestens vier Zeiteinheiten überlebt hat). Ebenso beginnt die X-Achse wieder bei 0, um die Zeit ab dem Zeitpunkt der Zensur zu messen. In diesem Beispiel beträgt die Median-Überlebenszeit für eine Person mit diesen erklärenden Variablen etwa fünf Zeiteinheiten (wobei die Kurve 0,5 auf der ursprünglichen Y-Achse schneidet). Wenn jedoch bekannt ist, dass die Person bereits vier Zeiteinheiten überlebt hat, beträgt die mediane zusätzliche Überlebenszeit etwa zwei Zeiteinheiten (wobei die Kurve 0,5 auf der kleineren, neu skalierten Y-Achse schneidet) bei einer Gesamtlebensdauer von sechs Zeiteinheiten. Mit anderen Worten: Wenn man weiß, dass die Person bereits vier Zeiteinheiten überlebt hat, erhöht sich die gesamte Median-Lebensdauer von etwa fünf Zeiteinheiten auf etwa sechs Zeiteinheiten. Je länger die Beobachtung vor der Zensur überlebt, um so länger wird sie voraussichtlich im Vergleich zu ihrer Basisüberlebenskurve überleben.

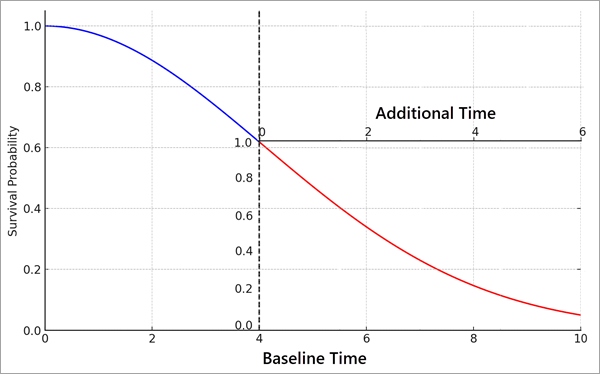
Bei zensierten Beobachtungen werden die Überlebenskurven, die die zusätzlichen Zeiten bis zum Ereignis nach der Zensur anzeigen, in den Pop-up-Diagrammen der Ausgabe-Features oder -Tabellen angezeigt. Sowohl für zensierte als auch für unzensierte Features werden auch die individuellen Überlebenskurven in den Pop-up-Diagrammen angezeigt.

Das Alter der Beobachtung zum Zeitpunkt der Zensur entspricht in der Regel dem aktuellen Alter der Beobachtung, kann aber auch das Alter sein, in dem die Person zuletzt beobachtet wurde, z. B. das Datum der zuletzt durchgeführten Brückeninspektion. In diesem Fall beginnt die zusätzliche Überlebenszeit im dem Alter der Beobachtung, als sie zuletzt stattgefunden hat.

Kaplan-Meier-Kurve

Da jede Kombination von erklärenden Variablen zu einer anderen Überlebenskurve führt, kann es schwierig sein, zu quantifizieren, ob eine bestimmte Beobachtung eine längere oder kürzere Lebensdauer als eine typische Beobachtung haben wird. Einige der erklärenden Variablen der Beobachtung verlängern die Lebensdauer, andere verkürzen sie. Es ist jedoch nicht klar, ob sie zusammengenommen die Lebensdauer der Beobachtung verlängern oder verkürzen. Um eine Kurve zu erstellen, die als Grundlage für den Vergleich mit individuellen Überlebenskurven verwendet werden kann, berechnet das Werkzeug eine Kaplan-Meier-Kurve für die Daten.

Die Kaplan-Meier-Kurve ist eine nichtparametrische Schätzung der Überlebensfunktion, die erklärende Variablen ignoriert und den Anteil der Beobachtungen schätzt, bei denen das Ereignis im Laufe der Zeit nicht eingetreten ist. Dies geschieht durch schrittweise Anpassung der Zeitpunkte des Ereignisses und der Zensur anhand der folgenden Gleichung:

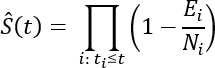
In der Gleichung ist E_i die Anzahl der Ereignisse, die zum Zeitpunkt t_i eingetreten sind, und N_i ist die Anzahl der Beobachtungen, bei denen das Ereignis nicht eingetreten ist oder die vor dem Zeitpunkt t_i zensiert wurden.

Die Kurve wird als Treppenfunktion dargestellt, die jedes Mal abnimmt, wenn das Ereignis eintritt. Die Kurve kann sich nicht über den Zeitpunkt des größten Werts im Feld "Alter" erstrecken, und die Überlebenswahrscheinlichkeit wird nie unter den Prozentsatz der zensierten Personen fallen. In der untenstehenden Kaplan-Meier-Kurve lag der größte Wert des Feldes "Alter" beispielsweise bei etwa 3500 (der Maximalwert der X-Achse), und etwas mehr als 40 Prozent der Beobachtungen wurden zensiert (der kleinste Wert der Kurve liegt etwas über 0,4).

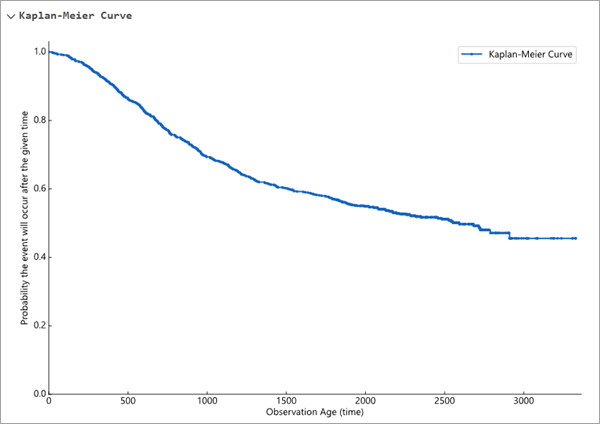
Die Kaplan-Meier-Kurve für die Daten wird in einem ausblendbaren Abschnitt der Geoverarbeitungsmeldungen angezeigt. Da sie auch in den Pop-up-Diagrammen der Ausgabe-Features oder -Tabelle angezeigt wird, kann sie direkt mit den Überlebenskurven einzelner Beobachtungen verglichen werden (weitere Informationen finden Sie im nächsten Abschnitt).

Werkzeugausgaben

Zur Untersuchung der Ergebnisse gibt das Werkzeug eine Vielzahl von Ausgaben zurück. Die Ausgaben umfassen eine Ausgabe-Feature-Class oder Tabelle, Geoverarbeitungsmeldungen, Pop-up-Diagramme und ein Histogramm.

Ausgabe-Features oder -Tabelle

Für die Feature-Eingabe ist die Darstellung des Ausgabe-Feature-Layers abhängig von der medianen zusätzlichen Zeit bis zum Ereignis. Zensierte Features sind in Rot- und Rosatönen gehalten, wobei dunklere Töne anzeigen, dass das Ereignis voraussichtlich früher eintreten wird. Unzensierte Features sind hellgrau gezeichnet und so konfiguriert, dass sie unter den zensierten Features dargestellt werden, wenn sich ihre Symbole überlappen.

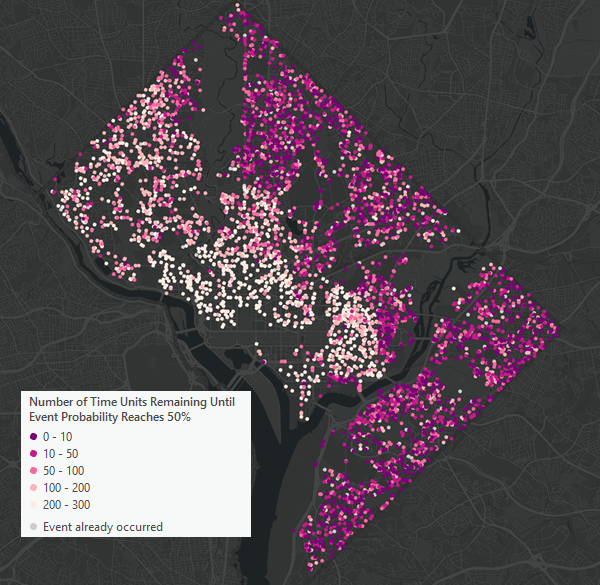
Sowohl bei Tabellen- als auch bei Feature-Eingaben enthält die Ausgabe Kopien aller Eingabefelder sowie verschiedene Quantile der zusätzlichen Zeit bis zum Ereignis. Die Felder enthalten das 5., 10., 25., Median (50.), 75., 90. und 95. Perzentil der zusätzlichen Zeit bis zum Ereignis. Sie können diese Werte verwenden, um Bereiche für den wahrscheinlichen Zeitpunkt des Ereignisses zu erstellen, z. B. durch Verwendung des 5. und 95. Perzentils zum Erstellen eines 90-prozentigen Konfidenzintervalls. Bei unzensierten Features sind alle Quantilfeldwerte NULL-Werte, da die Vorhersage, wann das Ereignis eingetreten wird, nicht notwendig ist, wenn das Ereignis bereits eingetreten ist.

Pop-up-Diagramme

Wenn der Parameter Pop-ups für Überlebenskurve aktivieren aktiviert ist, enthalten die Ausgabe-Features oder die -Tabelle auch ein Feld mit Pop-up-Diagrammen für jede Beobachtung. Bei Features können Sie auf die Pop-up-Diagramme zugreifen, indem Sie mit dem Werkzeug Erkunden auf das Feature in der Karte klicken. Bei Tabellen können die Pop-up-Diagramme durch Klicken mit der rechten Maustaste auf die Zeile des Datensatzes in der Attributtabelle aufgerufen werden.

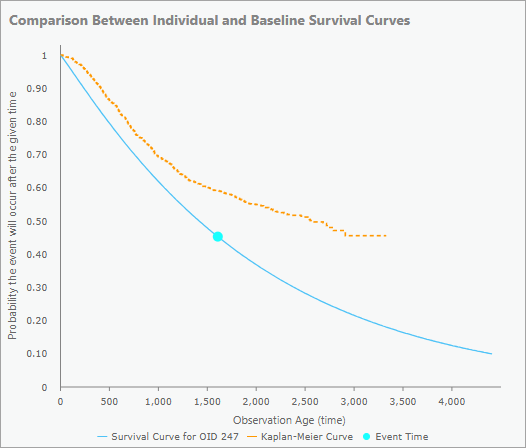
Für unzensierte Beobachtungen zeigt das Pop-up-Diagramm die Überlebenskurve für das Feature (blaue Kurve) und einen blauen Punkt, der den Zeitpunkt des Ereignisses angibt. So können Sie sehen, ob das Ereignis für die Beobachtung früh oder spät in ihrer vorhergesagten Lebensdauer eingetreten ist. Beobachtungen mit Ereignissen, die viel früher oder später als vom Modell erwartet eintreten, können weitere Untersuchungen rechtfertigen. Die Kaplan-Meier-Kurve (orangefarbene Kurve) ist ebenfalls im Pop-up-Diagramm enthalten und dient als Vergleichsgrundlage. So können Sie sehen, ob die Beobachtung länger oder kürzer als eine typische Beobachtung überleben sollte. In der Abbildung unten liegt die Überlebenskurve beispielsweise unterhalb und links von der Kaplan-Meier-Kurve. Dies bedeutet, dass das Ereignis früher eintreten sollte als bei den meisten anderen Beobachtungen. Der blaue Punkt befindet sich auch in der Mitte der Überlebenskurve. Dies bedeutet, dass das Ereignis ungefähr zu dem Zeitpunkt eingetreten ist, den das Modell auf der Grundlage seiner erklärenden Variablen vorhergesagt hat.

Hinweis:

Die X-Achse der Pop-up-Diagramme wird so erweitert, dass die Überlebenskurve 0,1 erreicht (ein Grenzwert ist erforderlich, da Überlebenskurven nie den Wert Null erreichen). Da sich die Kaplan-Meier-Kurve jedoch nicht über den größten Wert des Feldes "Alter" hinaus erstrecken kann, endet sie oft, bevor die Überlebenskurve 0,1 erreicht. Um sicherzustellen, dass die Kaplan-Meier-Kurve zu sehen ist, wird die X-Achse nie länger als doppelt so lang wie die Kaplan-Meier-Kurve sein, selbst wenn die Überlebenskurve noch nicht 0,1 erreicht.

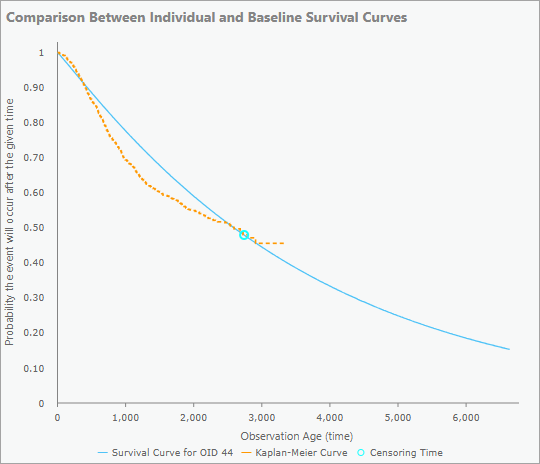
Bei zensierten Features enthalten die Pop-up-Diagramme zusätzlich die Überlebenskurve und die Kaplan-Meier-Kurve für die Beobachtung, aber der Zeitpunkt der Zensur wird durch einen blauen Kreis statt durch einen Punkt angezeigt.

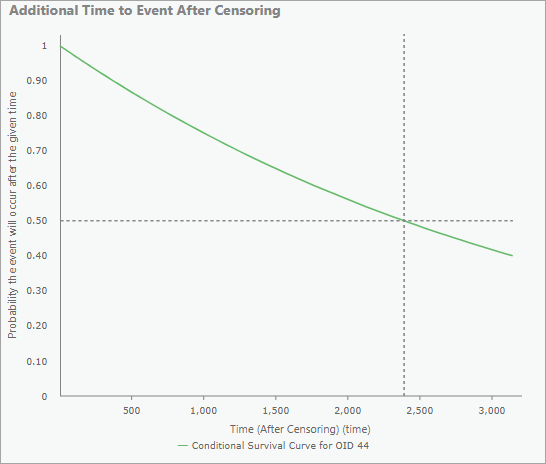
Nur bei zensierten Features enthalten die Pop-up-Diagramme auch ein Diagramm mit der zusätzlichen Zeit bis zum Ereignis nach dem Zeitpunkt der Zensur. Die mediane zusätzliche Zeit wird als gestrichelte horizontale und vertikale Linie dargestellt, um den Zeitpunkt zu kennzeichnen, zu dem das Modell mit einer Wahrscheinlichkeit von 50 Prozent vorhersagt, dass das Ereignis eingetreten sein wird. Die X-Achse wird so erweitert, dass die Überlebenskurve 0,4 erreicht, um sicherzustellen, dass der Medianwert immer zu sehen ist.

Um bestimmte Werte der Kurven anzuzeigen, können Sie mit der Maus auf ein beliebiges Pop-up-Diagramm zeigen.

Geoverarbeitungsmeldungen

Die Geoverarbeitungsmeldungen enthalten verschiedene Abschnitte, in denen die Auswirkungen der erklärenden Variablen und Diagnosen im Zusammenhang mit der Eignung des Modells für die Daten zusammengefasst werden.

Kontinuierliche erklärende Variablen

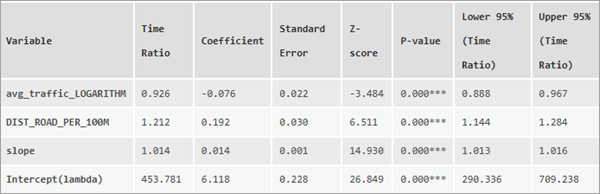
Der erste Abschnitt der Meldungen enthält eine Tabelle, in der die Auswirkungen der kontinuierlichen erklärenden Variablen zusammengefasst sind. Für jede Variable zeigt die Tabelle das Zeitverhältnis, den Koeffizienten und seinen Standardfehler (aus dem Skalenparameter der Weibull-Verteilung), den Z-Wert und den p-Wert, der die statistische Signifikanz des Koeffizienten testet, sowie die Unter- und Obergrenzen für ein 95-prozentiges Konfidenzintervall des Zeitverhältnisses an.

Am Ende ist eine Zeile für den Intercept-Term enthalten, aber die Rohwerte sind in der Regel nicht aussagekräftig. Der Zweck des Intercepts besteht stattdessen darin, die Überlebenskurven auf die Zeiteinheit des Feldes "Alter" zu skalieren. Wenn Sie beispielsweise die Werte des Feldes "Alter" von Stunden in Tage umrechnen, bleiben alle Zeitverhältnisse gleich, aber das Zeitverhältnis des Intercepts wird durch 24 (die Umrechnung von Stunden in Tage) geteilt. Aus diesem Grund muss die Einheit des Feldes "Alter" im Werkzeug nicht angegeben werden und liefert unabhängig von der Einheit gleichwertige Ergebnisse.

Hinweis:

Für jede Variable werden der Koeffizient und der Standardfehler direkt durch das Modell für beschleunigte Ausfallzeiten geschätzt und mit einem Z-Test auf statistische Signifikanz geprüft. Das Zeitverhältnis wird dann aus dem Koeffizienten berechnet, indem dessen Exponentialwert verwendet wird: exp(coefficent). Zeitverhältnisse werden in der Regel gegenüber Koeffizienten bevorzugt, da Zeitverhältnisse in Relation zur rohen Überlebenszeit interpretiert werden, während die Koeffizienten relativ zur logarithmierten Überlebenszeit interpretiert werden. Die obere und untere Konfidenzgrenze werden berechnet, indem ein Konfidenzintervall für den Koeffizienten erstellt und der Exponentialwert der Endpunkte berechnet wird.

Kategoriale erklärende Variablen

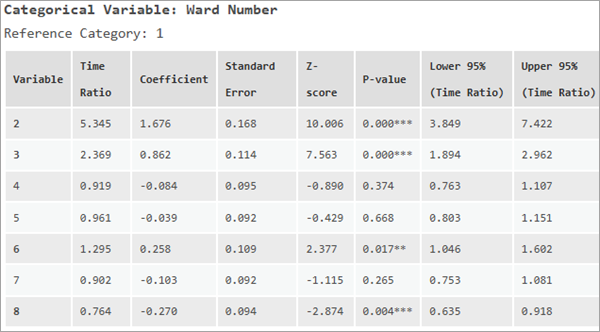
Der zweite Abschnitt der Meldungen enthält Tabellen, in denen die Auswirkungen der kategorialen erklärenden Variablen zusammengefasst sind. Für jede kategoriale Variable wird eine Tabelle angezeigt, die die Wirkung jeder ihrer Kategorien zeigt. Die Referenzkategorie wird über der Tabelle angezeigt und alle Zeitverhältnisse müssen im Verhältnis zu dieser Kategorie interpretiert werden. In der folgenden Abbildung ist die kategoriale Variable beispielsweise die Stadtteilnummer, und Stadtteil 1 ist die Referenzkategorie. Beobachtungen in Stadtteil 2 leben 5,345-mal länger als Beobachtungen in Stadtteil 1 (Zeitverhältnis gleich 5,345), aber Beobachtungen in Stadtteil 8 leben 23,6 Prozent kürzer als Beobachtungen in Stadtteil 1 (Zeitverhältnis gleich 0,764). Die p-Werte zeigen auch, dass sich die Stadtteile 4, 5 und 7 nicht signifikant von Stadtteil 1 unterscheiden.

Hinweis:

Jede kategoriale Variable wird in eine Reihe binärer (0 oder 1) Variablen umgewandelt, und diese binären Variablen werden als kontinuierliche erklärende Variablen im Modell für beschleunigte Ausfallzeiten verwendet. Für K-Kategorien (K-1) werden binäre Variablen erstellt, und jede Kategorie erhält eine binäre Variable mit Ausnahme der Referenzkategorie (dieser Prozess wird als Indikator-Encodierung bezeichnet). Eine Kategorie muss ausgeschlossen und als Referenz verwendet werden, da die Einbeziehung binärer Variablen für alle Kategorien zu einer perfekten Kollinearität führt, wodurch das Modell nicht in der Lage ist, die Koeffizienten und Zeitverhältnisse zu schätzen.

Weibull-Formparameter

Nach den Koeffiziententabellen der erklärenden Variablen zeigen die Meldungen eine Tabelle an, in der die Formparameter der Weibull-Verteilung zusammengefasst sind. Die Tabelle enthält auch den Z-Wert und den p-Wert, mit denen geprüft wird, ob der Formparameter statistisch von 1 verschieden ist. Untere und obere Grenzen für ein 95-prozentiges Konfidenzintervall werden ebenfalls angegeben.

Der Formparameter bestimmt, ob die Überlebenskurve beschleunigt oder verlangsamt wird. Werte, die signifikant größer als 1 sind, weisen auf eine Beschleunigung hin, d. h. je älter die Beobachtung ist, desto wahrscheinlicher ist es, dass das Ereignis in naher Zukunft eintritt. Werte, die signifikant unter 1 liegen, weisen auf eine Verlangsamung hin. Dies bedeutet, dass das Ereignis bei jüngeren Beobachtungen mit größerer Wahrscheinlichkeit in naher Zukunft eintreten wird. Werte, die nicht signifikant von 1 abweichen, deuten darauf hin, dass für jüngere und ältere Beobachtungen das Ereignis in naher Zukunft mit gleicher Wahrscheinlichkeit eintreten wird. Das Modell geht davon aus, dass sich die Überlebenskurve ständig beschleunigt oder verlangsamt, aber nicht zwischen diesen beiden Zuständen wechseln kann.

Modellzusammenfassung

Der letzte Abschnitt der Meldungen ist ein Abschnitt mit einer Modellzusammenfassung, der Statistiken zur Gesamtgenauigkeit der Vorhersagen und zur Eignung des Modells enthält. Der Abschnitt beinhaltet die folgenden Statistiken:

• Konkordanzindex: Ein Wert zwischen 0 und 1, der die Wahrscheinlichkeit angibt, dass das Modell korrekt vorhersagen kann, ob eine Person eine längere Lebenserwartung als eine andere Person hat. Werte nahe 1 zeigen an, dass das Modell fast immer vorhersagen kann, welche Person das Ereignis zuerst erleben wird, und Werte nahe 0,5 zeigen an, dass das Modell die Reihenfolge der Ereignisse nicht besser vorhersagen kann als der Zufall. Werte unter 0,5 werden selten beobachtet, würden aber bedeuten, dass die Vorhersage des Modells weniger genau ist als der Zufall. Der Wert wird als Anteil der paarweisen Personen berechnet, bei denen das Modell korrekt vorhergesagt hat, welche der beiden Personen das Ereignis zuerst erlebt hat. Zensierte Features werden nicht in die Berechnung einbezogen, da ihre Überlebenszeit nicht bekannt ist. In der Praxis liegt der Wert in der Regel zwischen 0,6 und 0,8.
• AIC: Das Akaike-Informationskriterium (AIC) für die Anpassung des Modells für beschleunigte Ausfallzeiten. Dieser Wert dient hauptsächlich zu Informationszwecken, kann aber auch in anspruchsvollen Workflows verwendet werden, z. B. zur Erstellung verschachtelter Likelihood-Quotienten-Tests zwischen verschiedenen Kombinationen erklärender Variablen.
• p-Wert: Der p-Wert für einen globalen Signifikanztest der erklärenden Variablen. Der Wert gibt an, ob die erklärenden Variablen zusammengenommen die Vorhersagen des Modells signifikant verbessern. Wenn dieser Wert nicht statistisch signifikant ist (in der Regel ein Wert größer als 0,05), ist die Leistung des Modells nicht signifikant besser als die Leistung ohne erklärende Variablen. Der Wert wird mithilfe eines Likelihood-Quotienten-Tests bestimmt.

Histogramm der Residuen der Abweichungen

Der Ausgabe-Feature-Layer enthält auch ein Histogramm der Residuen der Abweichungen der Beobachtungen. Residuen der Abweichungen sind konzeptionell ähnlich wie Residuen in anderen Regressionsmodellen, da sie quantifizieren, ob eine Beobachtung eine längere oder kürzere Lebensdauer hatte, als vom Modell vorhergesagt. Positive Werte für Residuen der Abweichungen bedeuten, dass die Person eine längere Lebensdauer hatte als vorhergesagt, und negative Werte für Residuen der Abweichungen bedeuten, dass die Person eine kürzere Lebensdauer hatte (beachten Sie, dass einige Quellen die Vorzeichen, positiv oder negativ, umgekehrt definieren). Wenn das Modell gut passt, sollten die Residuen der Abweichungen nahe Null liegen.

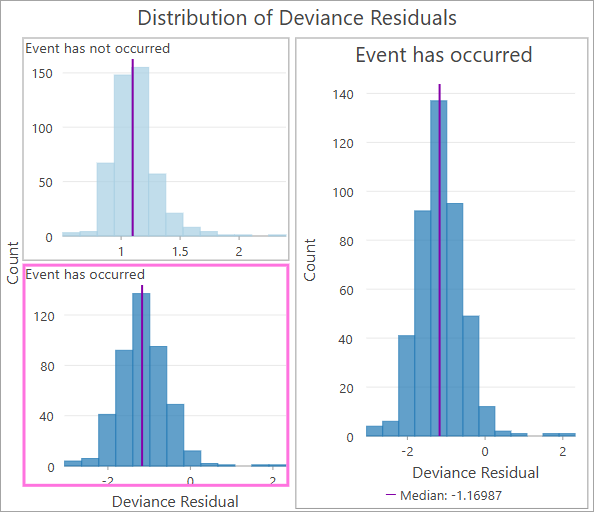
Bei unzensierten Beobachtungen haben einige eine längere oder kürzere Lebensdauer als vom Modell vorhergesagt, sodass ihre Residuen der Abweichungen sowohl positiv als auch negativ sein können. Residuen der Abweichungen für zensierte Beobachtungen sind jedoch immer positiv. Aus diesem Grund wird das Histogramm durch das Feld "Ereignisindikator" geteilt, sodass separate Histogramme für zensierte und unzensierte Beobachtungen angezeigt werden.

Residuen der Abweichungen sind am nützlichsten für die Untersuchung von Ausreißern in den Ergebnissen, und Extremwerte in beiden Histogrammen weisen auf unterschiedliche Dinge hin. Bei unzensierten Beobachtungen zeigen extrem negative Werte an, dass das Ereignis für die Beobachtung viel früher eingetreten ist als vom Modell vorhergesagt, und extrem positive Werte zeigen an, dass das Ereignis viel später eingetreten ist. Werte, die größer als drei in beide Richtungen sind, weisen wahrscheinlich auf Ausreißer oder anomale Beobachtungen hin, die weitere Untersuchungen oder eine Entfernung aus dem Dataset rechtfertigen könnten. Bei zensierten Beobachtungen sind die Werte weniger aussagekräftig, aber sie messen im Allgemeinen, wie weit die Beobachtung in ihrer Lebensdauer fortgeschritten war, bevor sie zensiert wurde. Werte ganz links (nahe Null) zeigen an, dass die Beobachtung sehr früh in ihrer Lebensdauer zensiert wurde, und Werte ganz rechts zeigen an, dass sie sehr spät in ihrer Lebensdauer zensiert wurde (möglicherweise hatte sie bereits eine längere Lebensdauer als vom Modell vorhergesagt, sogar schon vor der Zensur).

Residuen der Abweichungen werden mit der folgenden Gleichung berechnet:

In der Gleichung ist S-hat_i(t_i) die geschätzte Wahrscheinlichkeit des Überlebens für die Beobachtung zum Zeitpunkt des Ereignisses (oder zum Zeitpunkt der Zensur) und δ_i ist der Ereignisindikator.

Hinweis:

Residuen der Abweichungen für zensierte Beobachtungen sind immer positiv, denn wenn eine Person bereits eine beliebige Lebensdauer überlebt hat, wird vorausgesagt, dass sie eine längere Gesamtlebensdauer hat, als ihre Basislinie-Überlebenskurve vorhersagt (Erläuterungen hierzu finden Sie in der Abbildung im Abschnitt Zensierte Beobachtungen und Vorhersagen oben). Dieser Prozess stellt sicher, dass der Gesamtmittelwert der Residuen der Abweichungen (zensiert und unzensiert) bei ordnungsgemäß spezifizierten Modellen gleich Null ist.

Empfehlungen und Beschränkungen und empfohlener Workflow

Das Werkzeug ist mit einer Reihe von Einschränkungen und Herausforderungen verbunden, die auftreten können. Im Folgenden finden Sie allgemeine Empfehlungen und Best Practices für die Verwendung des Werkzeugs:

• Die Vorhersage, wann ein Ereignis in der Zukunft eintreten wird, ist von Natur aus eine schwierige Aufgabe. Daher sollten Sie realistische Erwartungen haben. Das Werkzeug kann nur Informationen aus den von Ihnen bereitgestellten erklärenden Variablen extrahieren, aber komplexe Phänomene wie Infrastrukturausfälle beinhalten zahlreiche Faktoren, die oft sehr lokal und individuell sind. In der Praxis sollten Sie die vorhergesagten Zeiten für das Ereignis in der Regel als allgemeine Hinweise darauf betrachten, wann das Ereignis eintreten könnte, und nicht als ganz konkrete Vorhersagen bestimmter Daten. Sie sollten auch besonders vorsichtig und skeptisch sein, wenn Sie über die maximale Dauer des längsten Ereignisses der Eingabedaten hinaus extrapolieren. Obwohl die Ergebnisse der Ereigniszeitanalyse oft ungenau sind, können sie dennoch sehr nützlich sein, um allgemeine Schätzungen zukünftiger Kosten vorzunehmen oder um Ressourcen für Beobachtungen zu priorisieren und zuzuweisen, bei denen das Ereignis am wahrscheinlichsten als Nächstes eintritt.

• Modelle vom Typ "Zeit bis zum Ereignis" sind nicht von Natur aus räumlich, aber die Einbeziehung räumlicher Informationen kann das Modell verbessern, indem geographische Muster berücksichtigt werden. Erwägen Sie, räumliche erklärende Variablen, wie zum Beispiel geographische Regionen, als kategoriale erklärende Variablen oder Entfernungen zu wichtigen Features als kontinuierliche erklärende Variablen hinzuzufügen. Zum Beispiel könnte bei der Modellierung der Sterblichkeit von Stadtbäumen die Entfernung zum nächsten Gebäude aufgrund des durch die Schatten der Gebäude verringerten Sonnenlichts eine wichtige Rolle spielen.

• Das Modell geht davon aus, dass das Ereignis nach einer gewissen Zeit bei jeder Beobachtung eintritt, aber es gibt einige Fälle, in denen dies nicht der Fall ist. Zum Beispiel werden bei der Vorhersage der Zeit bis zur erneuten Festnahme einige Personen nie erneut festgenommen, aber das Modell wird dennoch eine Überlebenskurve für sie vorhersagen. In der Praxis bedeutet dies, dass das Ereignis wahrscheinlich nie eintreten wird, wenn die vorhergesagte zusätzliche Überlebenszeit für eine Beobachtung sehr groß ist.
• Bei kontinuierlichen erklärenden Variablen sind die Zeitverhältnisse die multiplikative Änderung in der Überlebenskurve bei einer Erhöhung der erklärenden Variablen um eine Einheit. Bei einigen Variablen ist jedoch eine Änderung um eine Einheit verschwindend gering und führt zu Zeitverhältnissen, die selbst bei hochsignifikanten und wichtigen erklärenden Variablen sehr nahe bei 1 liegen. Bei der Vorhersage, wann Dächer repariert werden müssen, könnte beispielsweise die Größe des Gebäudes in Quadratmetern als erklärende Variable verwendet werden. Doch auch wenn die Größe des Gebäudes von großer Bedeutung ist, hat eine Vergrößerung um nur einen einzigen Quadratmeter nur geringe Auswirkungen auf die Überlebenskurve. Wenn eine Ihrer erklärenden Variablen hochsignifikant ist (hoher Z-Wert und niedriger p-Wert), aber ein gedrucktes Zeitverhältnis von 1,000 oder sehr nahe daran hat, sollten Sie in Betracht ziehen, die Werte des Feldes durch einen großen konstanten Wert zu teilen. Wenn man beispielsweise die Variable Quadratmeterzahl durch 100 teilt, erhält man identische Überlebenskurven und Signifikanzergebnisse, aber das Zeitverhältnis wird jetzt als Änderung für eine Vergrößerung der Gebäudefläche um 100 Quadratmeter interpretiert, was zu einem besser interpretierbaren Zeitverhältnis führen kann. Durch Multiplikation oder Division einer der erklärenden Variablen (oder des Feldes "Alter") mit einem konstanten Wert werden äquivalente Überlebenskurven erstellt. Daher sollten Sie die Werte neu skalieren, wenn dies bei der Interpretation der Ergebnisse hilfreich ist.
• Da das Zeitverhältnis multiplikativ ist, können große Werte (im Vergleich zu den Werten der restlichen Daten) einer kontinuierlichen erklärenden Variablen zu Instabilität und unangemessen langen oder kurzen Überlebenskurven führen. Das Zeitverhältnis stellt die Veränderung bei einer Erhöhung der erklärenden Variablen um eine Einheit dar, und diese erhöht sich exponentiell. Zum Beispiel streckt eine Erhöhung der erklärenden Variablen um fünf Einheiten die Überlebenskurve um das Zeitverhältnis hoch 5. Bei großen Werten der erklärenden Variablen können diese Exponenten sehr groß werden und zu instabilen Überlebenskurven führen. Ausreißer sind besonders problematisch, aber selbst große Werte, die keine Ausreißer sind, können zu instabilen Überlebenskurven führen. In diesen Fällen besteht eine mögliche Lösung darin, eine logarithmische Transformation auf die erklärende Variable anzuwenden. Dadurch wird das Zeitverhältnis für die erklärende Variable schwieriger zu interpretieren (es ist jetzt die Streckung der Überlebenskurve für eine Erhöhung im Logarithmus der erklärenden Variable um eine Einheit), aber die Konvertierung der erklärenden Variable in eine logarithmische Skala wirkt oft dem kumulativen Effekt des Zeitverhältnisses entgegen und führt zu sinnvolleren Überlebenskurven.

• Während die Schätzung der Modellparameter sowohl zensierte als auch unzensierte Beobachtungen verwendet, liefern unzensierte Beobachtungen die meisten Informationen, da ihre genaue Überlebenszeit bekannt ist. Im Allgemeinen wird empfohlen, mindestens 10 unzensierte Beobachtungen pro erklärender Variable zu verwenden. Kategoriale Variablen sollten jedoch als mehrere Variablen gezählt werden. Eine kategoriale Variable mit zwei Kategorien zählt als eine Variable; drei Kategorien zählen als zwei Variablen; vier Kategorien zählen als drei Variablen; usw. Zusätzlich sollte jede Kategorie mehrere unzensierte Beobachtungen enthalten, um die Wirkung aller Kategorien der kategorialen Variablen bestmöglich einschätzen zu können.

• In manchen Fällen kann es schwierig sein, den Startpunkt der Lebensdauer einer Beobachtung zu definieren. Beispielsweise werden Brücken regelmäßig repariert und gewartet. Bei der Vorhersage des Zeitpunkts der nächsten erforderlichen Reparaturen könnte das Startdatum das Datum sein, an dem die Brücke ursprünglich gebaut wurde, oder das Datum, an dem die Brücke zuletzt repariert wurde. In diesem Fall müssen Sie entscheiden, ob eine reparierte Brücke als gleichwertig mit einer neuen Brücke angesehen wird. Wenn Sie der Meinung sind, dass reparierte Brücken neuen Brücken gleichwertig sind, kann eine einzelne Brücke mehrmals in die Daten aufgenommen werden, um den Aufbau des Modells zu erleichtern (einmal für jede erforderliche Reparatur). Wenn Sie jedoch der Meinung sind, dass eine reparierte Brücke nicht mit einer neuen Brücke gleichzusetzen ist, können Sie versuchen, die Anzahl der vorherigen Reparaturen der Brücke als erklärende Variable zu verwenden.

Obwohl es keinen perfekten Workflow für die Ereigniszeitanalyse gibt, ist im Folgenden eine allgemeine Vorlage für die Erstellung und Bewertung eines Modells aufgeführt:

1. Untersuchen Sie die Eingabedaten und entscheiden Sie, welche erklärenden Variablen Sie verwenden möchten. Wählen Sie erklärende Variablen aus, von denen Sie wissen oder erwarten, dass sie mit der Überlebenszeit zusammenhängen, und erkunden Sie sie mithilfe von Diagrammen. Scatterplots von erklärenden Variablen im Vergleich zur Überlebenszeit sind besonders nützlich, um festzustellen, welche Variablen mit der Überlebenszeit zusammenhängen (dafür können leider nur unzensierte Beobachtungen verwendet werden). Achten Sie besonders auf Ausreißer in den kontinuierlichen erklärenden Variablen, und ziehen Sie in Betracht, diese zu entfernen oder eine logarithmische Transformation anzuwenden. Bei kategorialen Variablen sollten Sie sicherstellen, dass es für jede Kategorie mehrere unzensierte Beobachtungen gibt. Führen sie Kategorien mit einer geringen Anzahl unzensierter Beobachtungen zusammen oder entfernen Sie diese.
2. Je nachdem, wie die Daten vorliegen, kann für die Erstellung der Felder für Alter und Ereignisindikator ein erheblicher Aufwand an Datenbearbeitung erforderlich sein. Es ist zum Beispiel möglich, dass Sie Felder für Start- und Enddatum in Alterswerte umwandeln (hierfür ist die Verwendung des ArcadeArcade-Ausdrucks DateDiff im Werkzeug Feld berechnen nützlich) oder ein Textfeld in ein binäres Ereignisindikatorfeld umklassifizieren müssen.
3. Nachdem Sie das Werkzeug ausgeführt und alle Warnungen oder Fehler überprüft haben, sollten Sie die Gesamtgenauigkeit des Modells überprüfen und auf Anzeichen achten, die darauf hinweisen, dass das Modell möglicherweise unpassend ist oder falsch spezifiziert wurde. Überprüfen Sie das Histogramm der Residuen der Abweichungen, und achten Sie besonders auf extreme Residuenwerte (positiv oder negativ) in den unzensierten Beobachtungen. Bewerten Sie den p-Wert und den Konkordanzindex im Abschnitt "Modellzusammenfassung" der Meldungen. Wenn der p-Wert nicht signifikant ist (was selten der Fall sein wird), sollten Sie versuchen, erklärende Variablen zu finden, die zur besseren Schätzung der Überlebenszeiten beitragen. Sie sollten auch beurteilen, ob der Konkordanzindex akzeptabel hoch ist, und realistische Erwartungen haben.
4. Wenn das Gesamtmodell ausreichend genau ist, sollten Sie als Nächstes die Koeffiziententabellen in den Meldungen überprüfen, um zu erfahren, welche erklärenden Variablen sich auf die Überlebenszeiten ausgewirkt haben und wie stark ihr Einfluss war. Erwägen Sie, erklärende Variablen zu entfernen, die statistisch nicht signifikant sind.
5. Für Features erkunden Sie als Nächstes den Ausgabe-Feature-Layer in einer Karte und suchen nach räumlichen Mustern. Gibt es Gebiete, in denen die Überlebenszeit länger ist als in anderen?
6. Erkunden Sie schließlich die Pop-up-Diagramme und die Attributtabelle einzelner interessanter Beobachtungen, um ihre geschätzten Überlebenskurven zu sehen.

Referenzen

Bei der Implementierung des Werkzeugs wurden folgende Ressourcen verwendet:

• Collett, David. 2023. "Modelling survival data in medical research." Chapman und Hall/CRC. https://doi.org/10.1201/9781003282525.
• Davidson-Pilon, Cameron. 2019 "lifelines: survival analysis in Python." Journal of Open Source Software. 4(40), 1317, https://doi.org/10.21105/joss.01317.
• Klein, John P. und Melvin L. Moeschberger. 2003. "Survival Analysis: Techniques for Censored and Truncated Data." Springer Science & Business Media. ISBN 0-387-95399-X.