Die meisten statistischen Tests beginnen damit, dass eine NULL-Hypothese identifiziert wird. Die NULL-Hypothese für die Musteranalysewerkzeuge (Toolset "Analysen von Mustern" und Toolset "Cluster-Zuordnung") ist eine zufällige räumliche Verteilung (Complete Spatial Randomness, CSR), entweder von den Features selbst oder von den mit diesen Features verknüpften Werten. Die Z-Werte und p-Werte, die von den Musteranalysewerkzeugen zurückgegeben werden, geben Aufschluss darüber, ob Sie diese NULL-Hypothese ablehnen können oder nicht. Häufig werden Sie eines der Musteranalysewerkzeuge ausführen und hoffen, dass der Z-Wert und der p-Wert angeben, dass Sie die NULL-Hypothese ablehnen können, da dies darauf hindeuten würde, dass die Features (bzw. die mit den Features verknüpften Werte) eine statistisch signifikante Cluster-Bildung oder Streuung und kein zufälliges Muster aufweisen. Jedes Mal, wenn Sie eine räumliche Struktur, z. B. eine Cluster-Bildung, in der Landschaft (oder in den räumlichen Daten) sehen, ist dies der Beweis für zugrunde liegende räumliche Prozesse, die arbeiten. Als Geograph oder GIS-Analyst ist dies häufig das, woran Sie am meisten interessiert sind.
Der p-Wert ist eine Wahrscheinlichkeit. Für die Musteranalysewerkzeuge stellt dieser Wert die Wahrscheinlichkeit dar, dass das beobachtete räumliche Muster von einem zufälligen Prozess erzeugt wurde. Wenn der p-Wert sehr klein ist, bedeutet dies, dass es sehr unwahrscheinlich (kleine Wahrscheinlichkeit) ist, dass das beobachtete räumliche Muster das Ergebnis zufälliger Prozesse ist, deshalb können Sie die NULL-Hypothese ablehnen. Sicherlich fragen Sie sich: Was bedeutet klein? Gute Frage. Sehen Sie sich die folgende Tabelle und die Erläuterung dazu an.
Z-Werte sind Standardabweichungen. Wenn ein Werkzeug beispielsweise ein Z-Wert von +2,5 zurückgibt, würde das bedeuten, dass die Standardabweichungen 2,5 ist. Sowohl die Z-Werte als auch die p-Werte sind mit Standardnormalverteilung verknüpft, wie unten dargestellt.
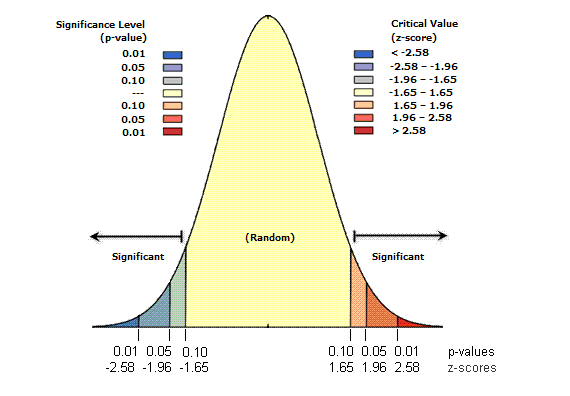
Sehr hohe oder sehr niedrige (negative) Z-Werte, die mit sehr kleinen p-Werten verknüpft sind, sind an den Enden der Normalverteilung zu finden. Wenn Sie ein Feature-Musteranalysewerkzeug ausführen und dabei niedrige p-Werte und entweder ein sehr hoher oder sehr niedriger Z-Wert zurückgegeben werden, deutet dies darauf hin, dass es unwahrscheinlich ist, dass das beobachtete räumliche Muster das theoretische zufällige Muster widerspiegelt, das von der NULL-Hypothese (CSR) dargestellt wird.
Um die NULL-Hypothese abzulehnen, müssen Sie ein subjektives Urteil bezüglich des Risikos fällen, das Sie bereit sind einzugehen, für den Fall, dass Sie falsch liegen (und die NULL-Hypothese fälschlicherweise ablehnen). Bevor Sie die räumliche Statistik ausführen, wählen Sie daher ein Konfidenzniveau aus. Typische Konfidenzniveaus liegen bei 90, 95 oder 99 Prozent. Ein Konfidenzniveau von 99 Prozent wäre in diesem Fall das konservativste und gibt an, dass Sie die NULL-Hypothese nicht ablehnen möchten, außer die Wahrscheinlichkeit, dass das Muster zufällig erstellt wurde, ist äußerst gering (weniger als 1 Prozent).
Konfidenzniveaus
In der Tabelle sind die kritischen p-Werte und Z-Werte für unterschiedliche Konfidenzniveaus dargestellt.
Hinweis:
Werkzeuge, die die Anwendung von FDR (False Discovery Rate) ermöglichen, verwenden korrigierte kritische p-Werte. Diese kritischen Werte sind mit den in der Tabelle aufgeführten Werten identisch oder kleiner als diese.
| Z-Wert (Standardabweichungen) | p-Wert (Wahrscheinlichkeit) | Konfidenzniveau |
|---|---|---|
< -1,65 oder > +1,65 | < 0,10 | 90% |
< -1,96 oder > +1,96 | < 0,05 | 95% |
< -2,58 oder > +2,58 | < 0,01 | 99% |
Sehen Sie sich das folgende Beispiel an. Die kritischen Z-Werte bei Verwendung eines Konfidenzniveaus von 95 Prozent sind die Standardabweichungen -1,96 und +1,96. Der nicht korrigierte, mit einem Konfidenzniveau von 95 Prozent verknüpfte p-Wert ist 0,05. Wenn der Z-Wert zwischen -1,96 und +1,96 liegt, ist der nicht korrigierte p-Wert größer als 0,05, und Sie können die NULL-Hypothese nicht ablehnen; das gezeigte Muster könnte mit großer Wahrscheinlichkeit das Ergebnis zufälliger räumlicher Prozesse sein. Wenn der Z-Wert außerhalb dieses Bereichs liegt (z. B., -2,5 oder +5,4 Standardabweichungen) ist die Wahrscheinlichkeit groß, dass das beobachtete räumliche Muster zu ungewöhnlich und somit nicht das Ergebnis zufälliger Prozesse ist. Der p-Wert ist daher klein. In diesem Fall können Sie die NULL-Hypothese ablehnen und sich überlegen, wodurch die statistisch signifikante räumliche Struktur in den Daten verursacht wird.
Wesentlich ist hierbei, dass die Werte in der Mitte der Normalverteilung (beispielsweise Z-Werte wie 0,19 oder -1,2) das erwartete Ergebnis darstellen. Wenn jedoch der absolute Wert des Z-Wertes groß ist und die Wahrscheinlichkeiten niedrig sind (an den Enden der Normalverteilung) ist etwas ungewöhnliches und in der Regel sehr interessantes zu beobachten. Für das Werkzeug Hot-Spot-Analyse bedeutet "ungewöhnliches" beispielsweise entweder einen statistisch signifikanten Hot-Spot oder einen statistisch signifikanten Cold-Spot.
FDR-Korrektur
Die lokalen Werkzeuge zur Analyse räumlicher Muster, darunter Hot-Spot-Analyse und Cluster- und Ausreißeranalyse (Anselin Local Morans I) stellen den optionalen booleschen Parameter FDR-Korrektur anwenden (False Discovery Rate) zur Verfügung. Bei Aktivierung dieses Parameters werden die Schwellenwerte der in der Tabelle oben aufgeführten kritischen p-Werte durch das FDR-Verfahren (False Discovery Rate) potenziell reduziert, um Mehrfachtests und räumliche Abhängigkeit einzubeziehen. Die Reduzierung (falls zutreffend) ist eine Funktion der Anzahl der Eingabe-Features und der verwendeten Nachbarschaftsstruktur.
Lokale Werkzeuge zur Analyse räumlicher Muster beziehen jedes Feature im Kontext benachbarter Features ein und ermitteln, ob sich das lokale Muster (ein Ziel-Feature und dessen Nachbarn) statistisch vom globalen Muster (alle Features im Dataset) unterscheidet. Anhand der mit jedem Feature verknüpften Z-Werte und p-Werte wird ermittelt, ob die statistische Differenz signifikant ist oder nicht. Dieser analytische Ansatz führt zu Problemen bei Mehrfachtests und Abhängigkeiten.
Mehrfachtests – Mit einem Konfidenzniveau von 95 Prozent, besagt die Wahrscheinlichkeitstheorie, dass in 5 von 100 Fällen ein räumliches Muster strukturiert (z. B. geclustert oder gestreut) und mit einem statistisch signifikanten p-Wert verknüpft sein kann, wenn die zugrunde liegenden räumlichen Prozesse, die das Muster fördern, tatsächlich zufällig sind. In diesen Fällen würde die CSR-NULL-Hypothese aufgrund der statistisch signifikanten p-Werte fälschlicherweise abgelehnt. "Fünf von 100 Fällen" scheint ein ziemlich konservativer Wert zu sein, es sei denn, Sie berücksichtigen, dass räumliche Statistiken für jedes Feature im Dataset einen Test ausführen. Wenn beispielsweise 10.000 Features vorhanden sind, werden 500 falsche Ergebnisse erwartet.
Räumliche Abhängigkeit – Features, die sich räumlich nah sind, ähneln sich häufig; diesen Abhängigkeitstyp weisen meist räumliche Daten auf. Trotzdem erfordern viele statistische Tests, dass Features unabhängig sind. Für lokale Musteranalysewerkzeuge ist dies erforderlich, da die räumliche Abhängigkeit die statistische Signifikanz künstlich erhöhen kann. Die räumliche Abhängigkeit wird durch Musteranalysewerkzeuge verstärkt, da jedes Feature innerhalb des Kontextes seiner Nachbarn evaluiert wird und Features mit räumlicher Nähe möglicherweise viele gemeinsame Nachbarn aufweisen. Durch diese Überschneidung wird die räumliche Abhängigkeit akzentuiert.
Es gibt mindestens drei Methoden, Probleme im Zusammenhang mit Mehrfachtests und räumlicher Abhängigkeit anzugehen. Die erste Methode besteht darin, das Problem zu ignorieren, indem der für jedes Feature im Dataset ausgeführte Einzeltest isoliert betrachtet wird. Bei dieser Methode ist es jedoch sehr wahrscheinlich, dass einige statistisch signifikante Ergebnisse falsch sind (sie scheinen statistisch signifikant zu sein, obgleich die zugrunde liegenden räumlichen Prozesse in Wirklichkeit zufällig sind). Bei der zweiten Methode kommt ein klassisches Verfahren für Mehrfachtests wie Bonferroni- oder Sidak-Korrekturen zur Anwendung. Diese Methoden sind in der Regel jedoch zu konservativ. Während die Anzahl der falschen positiven Ergebnisse zwar in hohem Maße reduziert wird, werden keine statistisch signifikanten Ergebnisse gefunden, auch wenn sie vorhanden sind. Die dritte Methode sieht die Anwendung der FDR-Korrektur vor, bei der die Anzahl der falschen positiven Ergebnisse für ein bestimmtes Konfidenzniveau geschätzt und der kritische p-Wert entsprechend angepasst wird. Bei dieser Methode werden statistisch signifikante p-Werte vom kleinsten (stärksten) bis zum größten (schwächsten) Wert geordnet, wobei auf Grundlage der geschätzten falschen positiven Werte die schwächsten Werte aus der Liste entfernt werden. Die restlichen Features mit statistisch signifikanten p-Werten werden anhand des Gi_Bin- oder COType-Feldes in der Ausgabe-Feature-Class identifiziert. Obwohl diese Methode nicht perfekt ist, zeigen empirische Tests, dass sie bessere Ergebnisse erzielt als die isolierte Ausführung lokaler Tests oder die Anwendung herkömmlicher, höchst konservativer Mehrfachtestmethoden. Weitere Informationen zur FDR-Korrektur finden Sie im Abschnitt "Zusätzliche Quellen".
Die NULL-Hypothese und räumliche Statistik
Mehrere Statistiken in der Toolbox "Spatial Statistics" sind schlussfolgernde räumliche Musteranalysetechniken, z. B. Räumliche Autokorrelation (Morans I), Cluster-und Ausreißeranalyse (Anselin Local Morans I) und Hot-Spot-Analyse (Getis-Ord Gi*). Schlussfolgernde Statistiken beruhen auf der Wahrscheinlichkeitstheorie. Die Wahrscheinlichkeit ist ein Messwert für den Zufall, und alle statistischen Tests (entweder direkt oder indirekt) sind im Grunde Wahrscheinlichkeitsberechnungen, die die Rolle der Wahrscheinlichkeit für das Ergebnis der Analyse bewerten. In der Regel arbeiten Sie bei herkömmlichen (nicht räumlichen) Statistiken mit einer zufälligen Probe und versuchen, die Wahrscheinlichkeit zu bestimmen, mit der die Referenzdaten eine gute Darstellung der Bevölkerung insgesamt (reflektiv) sind. Sie könnten beispielsweise fragen: "Wie groß ist die Wahrscheinlichkeit, dass die Ergebnisse meiner Wählerbefragung (die aussagt, dass Kandidat A Kandidat B knapp schlagen wird) die finalen Wahlergebnisse widerspiegeln?" Bei vielen räumlichen Statistiken, einschließlich der oben aufgeführten räumlichen Autokorrelations-Typstatistiken, müssen Sie jedoch häufig mit allen verfügbaren Daten für das Untersuchungsgebiet arbeiten (alle Verbrechen, alle Krankheitsfälle, Attribute für jeden Zählbezirk usw.) Wenn Sie eine Statistik für die ganze Bevölkerung berechnen, haben Sie keine Schätzung mehr. Es handelt sich vielmehr um eine Tatsache. Es ist daher nicht sinnvoll, weiter über Wahrscheinlichkeiten zu sprechen. Wie können die räumlichen Musteranalysewerkzeuge, die häufig auf alle Daten im Untersuchungsgebiet angewendet wurden, Wahrscheinlichkeiten zulässig melden? Dies ist möglich, indem über die NULL-Hypothese vorausgesetzt wird, dass die Daten tatsächlich Teil einer größeren Population sind. Sehen Sie sich dies etwas genauer an.
Die Zufalls-NULL-Hypothese – Die Werkzeuge in der Toolbox "Spatial Statistics" verwenden, wenn möglich, die Zufalls-NULL-Hypothese als Grundlage für statistische Signifikanztests. Die Zufalls-NULL-Hypothese fordert, dass das beobachtete räumliche Muster der Daten eine von vielen (n!) möglichen räumlichen Anordnungen darstellt. Wenn Sie die Datenwerte aufnehmen und sie auf die Features im Untersuchungsgebiet werfen könnten, würden Sie eine mögliche räumliche Anordnung dieser Werte erhalten. (Beachten Sie, dass das Aufnehmen der Datenwerte und das zufällige Werfen ein Beispiel für einen zufälligen räumlichen Prozess ist). Die Zufalls-NULL-Hypothese besagt, dass wenn Sie diese Übung (aufnehmen, abwerfen) unendliche Male ausführen könnten, in den meisten Fällen ein Muster entstehen würde, das sich nicht wesentlich von dem beobachteten Muster (den realen Daten) unterscheidet. Hin und wieder werfen Sie vielleicht versehentlich alle höchsten Werte in die gleiche Ecke des Untersuchungsgebiets, die Wahrscheinlichkeit hierfür ist jedoch niedrig. Die Zufalls-NULL-Hypothese besagt, dass die Daten eine von vielen, viele, viele mögliche Versionen der zufälligen räumlichen Verteilung sind. Die Datenwerte sind fest; nur ihre räumliche Anordnung ist veränderbar.
Die Normalisierungs-NULL-Hypothese – Eine häufig verwendete alternative NULL-Hypothese, die nicht für die Toolbox "Spatial Statistics" implementiert wurde, ist die Normalisierungs-NULL-Hypothese. Die Normalisierungs-NULL-Hypothese fordert, dass die beobachteten Werte über einen zufälligen Sampling-Prozess von einer unendlich großen, normal verteilten Population von Werten abgeleitet werden. Bei einer anderen Probe würden Sie andere Werte erhalten, Sie würden aber dennoch erwarten, dass diese Werte für eine größere Verteilung repräsentativ sind. Die Normalisierungs-NULL-Hypothese gibt an, dass die Werte einen von vielen möglichen Beispielwerten darstellen. Wenn Sie die beobachteten Daten an eine normale Kurve anpassen und zufällig Werte aus dieser Verteilung auswählen könnten, die auf das Untersuchungsgebiet geworfen werden, würde meistens ein Muster und eine Verteilung von Werten erstellt werden, die sich nicht wesentlich von dem beobachteten Muster/der beobachteten Verteilung (den realen Daten) unterscheiden würde. Die Normalisierungs-NULL-Hypothese besagt, dass die Daten und ihre Anordnung eines von vielen, vielen, vielen möglichen zufälligen Beispielen sind. Weder die Datenwerte noch ihre räumliche Anordnung sind fest. Die Normalisierungs-NULL-Hypothese ist nur geeignet, wenn die Datenwerte normal verteilt sind.
Zusätzliche Ressourcen
- Ebdon, David. Statistics in Geography. Blackwell, 1985.
- Mitchell, Andy. The ESRI Guide to GIS Analysis, Volume 2. ESRI Press, 2005.
- Goodchild, M.F., Spatial Autocorrelation. Catmog 47, Geo Books, 1986
- Caldas de Castro, Marcia, and Burton H. Singer. "Controlling the False Discovery Rate: A New Application to Account for Multiple and Dependent Test in Local Statistics of Spatial Association." Geographical Analysis 38, pp 180-208, 2006.