Funktionsweise von "Geographisch gewichtete Regression (Multiscale) (MGWR)"

Das Werkzeug Geographisch gewichtete Regression mit mehreren Maßstäben (MGWR) führt erweiterte räumliche Regressionstechniken aus, die für Geographie, Stadtplanung und verschiedene andere Disziplinen genutzt werden. Es wurde aus dem Modell Geographisch gewichtete Regression (GWR) entwickelt, für das erklärende und abhängige Variablen innerhalb der Nachbarschaft eines Ziel-Features eingesetzt werden, um ein lokales lineares Regressionsmodell für die Interpretation oder Vorhersage zu konstruieren.

Die Hauptmotivation von GWR besteht darin, dass es zu restriktiv sein kann, wenn nur ein Regressionsmodell für eine große geographische Region verwendet wird. GWR lässt stattdessen an jeder räumlichen Position ein anderes Regressionsmodell zu, deren Regressionskoeffizienten sich über die Region gleichmäßig ändern. Das bedeutet, dass an verschiedenen Positionen im Untersuchungsgebiet die erklärenden Variablen unterschiedliche Auswirkungen auf die abhängige Variable haben. Dazu erstellt GWR für jedes räumliche Feature ein gewichtetes Regressionsmodell anhand der erklärenden und abhängigen Variablen des Features und dessen räumlichen Nachbarn. Nachbarn, die sich näher am Feature befinden, erhalten höhere Gewichtungen und haben größeren Einfluss auf das lokale Regressionsmodell.

MGWR ist eine Erweiterung von GWR, bei der die Nachbarschaft um jedes räumliche Feature zwischen den einzelnen erklärenden Variablen variieren kann. Das bedeutet, dass für einige erklärende Variablen die Nachbarschaft größer oder größer kleiner sein kann als für andere Variablen. Das Zulassen unterschiedlicher Nachbarschaften für verschiedene erklärende Variablen ist wichtig, da die Beziehungen zwischen den erklärenden Variablen und der abhängigen Variable bei unterschiedlichen räumlichen Maßstäben wirken können: Koeffizienten einiger Variablen können sich über das Untersuchungsgebiet hinweg allmählich ändern, während sich Koeffizienten anderer Variablen schnell ändern. Der Abgleich der Nachbarschaft jeder erklärenden Variable mit dem räumlichen Maßstab der erklärenden Variable ist der Grund, weshalb MGWR die Koeffizienten des lokalen Regressionsmodells genauer schätzen kann.

MGWR ist für große Datasets gut geeignet, die mindestens mehrere Hundert Features und Datasets enthalten, in denen die abhängige Variable räumliche Heterogenität aufweist. Um räumlich variierende Beziehungen in kleineren Datasets zu modellieren, können andere Werkzeuge besser geeignet sein. Das aktuelle Werkzeug Geographisch gewichtete Regression (Multiscale) (MGWR) akzeptiert nur kontinuierliche abhängige Variablen. Führen Sie das Modell nicht mit binären oder Zahldaten aus. Dies kann zu einem verzerrten Modell und bedeutungslosen Ergebnissen führen.

In diesem Thema wird MGWR vorwiegend anhand von Vergleichen mit anderen Regressionsmethoden erläutert. Es ist hilfreich, wenn Sie die Grundlagen der OLS-Regression (Ordinary Least Squares, kleinste Quadrate) kennen und mit Nachbarschaften, Gewichtungsschemas und Diagnosen in GWR vertraut sind, bevor Sie fortfahren.

Weitere Informationen zur OLS-Regression

Weitere Informationen zu GWR

Auswahl des Regressionsmodells

OLS, GWR und MGWR sind lineare Regressionsmodelle, sie werden jedoch für unterschiedliche räumliche Maßstäbe eingesetzt und treffen unterschiedliche Annahmen zur räumlichen Heterogenität (Konsistenz der Beziehungen im Untersuchungsgebiet) eines Datasets. OLS ist ein globales Modell. Es wird angenommen, dass die Datengenerierung im Raum stationär ist. Daher kann ein einziger Koeffizient überall die Beziehung zwischen den einzelnen erklärenden Variablen und den abhängigen Variablen abdecken. GWR ist ein lokales Modell, dass die Annahme der räumlichen Stationarität abschwächt, indem die Koeffizienten im Raum variieren können. In GWR wird allerdings angenommen, dass alle lokalen Beziehungen den gleichen räumlichen Maßstab nutzen, indem gefordert wird, dass alle erklärenden Variablen die gleiche Nachbarschaft verwenden. Wenn zum Beispiel eine erklärende Variable 20 Nachbarn einsetzt, müssen alle erklärenden Variablen auch 20 Nachbarn verwenden.

Bei MGWR können nicht nur die Koeffizienten im Raum variieren, sondern auch der Maßstab über unterschiedliche erklärende Variablen. MGWR nutzt dafür separate Nachbarschaften für jede erklärende Variable, um unterschiedliche räumliche Maßstäbe der Beziehungen zwischen jeder erklärenden Variablen und der abhängigen Variablen zu berücksichtigen. Dies ermöglicht die Kombination von erklärenden Variablen, die für relativ große räumliche Maßstäbe eingesetzt werden, z. B. Temperatur oder atmosphärischer Druck, mit Variablen, die in kleineren Maßstäben verwendet werden, z. B. Bevölkerungsdichte oder mittleres Einkommen.

MGWR schätzt lokale Koeffizienten genauer, und Probleme mit Multikollinearität treten seltener auf als bei GWR. Allerdings ist die Verarbeitungszeit bei MGWR viel länger als bei GWR, insbesondere für die Optionen Golden Search, Manuelle Intervalle und Benutzerdefiniert des Parameters Auswahlmethode für Nachbarschaften. Diese drei Methoden zur Auswahl der Nachbarschaft basieren auf dem Backfitting-Algorithmus ("Rückanpassung"), der sehr rechen- und speicherintensiv ist. Mit dem Umfang der Daten nehmen auch die Ausführungszeit und die Speicherauslastung signifikant zu.

Um zu entscheiden, welches Modell auf Ihre Daten angewendet werden soll, bedenken Sie die folgenden Fragen:

• Soll das Modell lokal oder global ausgeführt werden?
  • Wenden Sie für ein lokales Modell GWR oder MGWR an. Verwenden Sie andernfalls OLS oder ein anderes Modell wie das Werkzeug Forest-basierte Klassifizierung und Regression.
• Verwenden die erklärenden Variablen in meinem Modell unterschiedliche räumliche Maßstäbe?
  • Wenn Sie vermuten, dass die erklärenden Variablen unterschiedliche Maßstäbe verwenden könnten und sie die unterschiedlichen Maßstäbe identifizieren und modellieren möchten, wenden Sie MGWR an.
• Wie groß ist das Dataset? Wie lange kann ich auf die Ergebnisse warten?
  • Wenn Ihr Dataset sehr groß ist und Sie das Werkzeug MGWR ausführen, müssen Sie wahrscheinlich länger auf die Werkzeugausführung warten. Mit der gängigen Hardware der frühen 2020er Jahre (16 logische Prozessoren und 32 GB Speicher) und mit typischen Parametern beträgt die Laufzeit für Datasets mit mehr als 10.000 Punkten wahrscheinlich mehrere Stunden. Bei 50.000 kann die Laufzeit mehrere Tage betragen. Bei 100.000 oder mehr sind Speicherfehler wahrscheinlich.

Wenn Sie weiterhin unsicher sind, welches lokale Modell, GWR oder MGWR, Sie auf Ihre Daten anwenden sollten, beginnen Sie mit MGWR. Bei der Ausführung von MGWR wird auch GWR mit bestimmten Einstellungen ausgeführt. In den Geoverarbeitungsmeldungen finden Sie die GWR-Diagnosen und können sie mit den Diagnosen von MGWR vergleichen. Alternativ können Sie mehrere Werkzeuge ausführen (OLS, GWR und MGWR) und mit den AICc aus den Geoverarbeitungsmeldungen die Modelle vergleichen, um das beste auszuwählen. Wenn Sie mehrere Werkzeuge ausführen, skalieren Sie alle Modelle, oder lassen Sie alle Modelle nicht skaliert, um sicherzustellen, dass die Ausgaben vergleichbar sind.

Potenzielle Anwendungsbereiche

MGWR kann viele multivariate Analysen und Fragen anwenden, beispielsweise die folgenden:

• Welchen Einfluss haben verschiedene Features wie die Anzahl der Räume, das Baujahr, die Grundstücksgröße usw. auf den Preis eines Hauses? Unterscheiden sich die Beziehungen in unterschiedlichen Gemeinden erheblich?
• Wie ist die Verteilung von PM2.5 mit ökonomischen Variablen verknüpft, beispielsweise mit dem regionalen Haushaltseinkommen, der Anzahl von Autos pro Haushalt oder dem Prozentsatz des Bruttoinlandsprodukts durch Landwirtschaft?
• Welchen Einfluss haben im Präzisionsackerbau die Bodenbedingungen auf den Ertrag, wenn derselbe räumliche Maßstab als atmosphärische Variablen, wie Temperatur, Feuchtigkeit und Niederschlag, verwendet wird?

Überlegungen zu Performance und Benchmarks

Verschiedene Faktoren beeinflussen die MGWR-Laufzeit. Der wichtigste Faktor für die Laufzeit ist die Anzahl der Features. Die Laufzeit nimmt mit der Anzahl der Features kubisch exponentiell zu. Die Nachbarschaftsgröße und die Anzahl der erklärenden Variablen haben ebenfalls Einfluss auf die MGWR-Laufzeit, da mehr Berechnungen für jedes lokale Modell erforderlich werden. Um die Ergebnisse möglichst schnell zu berechnen, nutzt MGWR die parallele Verarbeitung auf Ihrem Computer. Bei einigen Berechnungen werden alle verfügbaren Kerne genutzt. Andere Berechnungen können dagegen durch die Umgebung Faktor für parallele Verarbeitung gesteuert werden.

Werkzeugeingaben

Es gibt verschiedene Methoden, um den räumlichen Maßstab der erklärenden Variablen anzugeben.

Auswahl der Nachbarschaft (Bandbreite)

Eine wichtige Verbesserung von MGWR ist, dass die Bandbreite (Nachbarschaft) der einzelnen erklärenden Variablen in der linearen Regressionsgleichung variieren kann. Die Nachbarschaft einer erklärenden Variablen an der Zielposition umfasst alle Positionen, die zur Schätzung des Koeffizienten der erklärenden Variablen im lokalen linearen Regressionsmodell beitragen. Jede Nachbarschaft wird durch eine Anzahl der Nachbarn um das Ziel-Feature oder durch alle Nachbarn innerhalb einer festen Entfernung definiert. Die Anzahl der Nachbarn oder die Entfernung kann für die einzelnen erklärenden Variablen unterschiedlich sein.

Für den Parameter Auswahlmethode für Nachbarschaften gibt es vier Optionen. Der Parameter kann verwendet werden, um den optimalen räumlichen Maßstab für jede erklärende Variable zu schätzen:

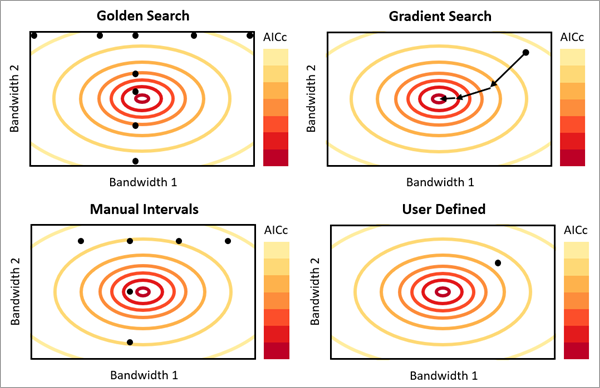
• Golden Search: Bestimmt die Anzahl der Nachbarn oder das Entfernungsband für jede erklärende Variable mithilfe des Golden-Search-Algorithmus. Bei dieser Methode werden mehrere Kombinationen von Werten für jede erklärende Variable zwischen einem angegebenen Minimal- und Maximalwert gesucht. Der Prozess ist iterativ. Er verwendet die Ergebnisse von vorherigen Werten, um jeweils eine neue zu testende Kombination auszuwählen. Die Werte, die zum Schluss ausgewählt werden, weisen den kleinsten AICc auf. Für die Option "Anzahl der Nachbarn" werden der Minimal- und der Maximalwert mit den Parametern Minimale Anzahl von Nachbarn und Maximale Anzahl von Nachbarn angegeben. Für die Option "Entfernungsband" werden der Minimal- und der Maximalwert mit den Parametern Minimale Suchentfernung und Maximale Suchentfernung angegeben. Die Mindest- und Maximalwerte werden für alle erklärenden Variablen übernommen. Die geschätzte Anzahl der Nachbarn oder das Entfernungsband sind jedoch für jede erklärende Variable unterschiedlich (sofern nicht zwei oder mehr Variablen zufällig denselben räumlichen Maßstab aufweisen). Bei dieser Option dauert die Berechnung am längsten, insbesondere bei großen oder hochdimensionalen Datasets.

• Gradientensuche: Bestimmt die Anzahl der Nachbarn oder das Entfernungsband für jede erklärende Variable mithilfe eines Gradienten-basierten Optimierungsalgorithmus. Um die optimale Bandbreite für jede erklärende Variable zu finden, verwendet die Gradientensuche die Ableitung von AICc in Bezug auf die Bandbreiten und aktualisiert die Bandbreiten, bis der kleinste AICc-Wert gefunden ist. Für die Option "Anzahl der Nachbarn" werden der Minimal- und der Maximalwert mit den Parametern Minimale Anzahl von Nachbarn und Maximale Anzahl von Nachbarn angegeben. Für die Option Entfernungsband werden der Minimal- und der Maximalwert mit den Parametern Minimale Suchentfernung und Maximale Suchentfernung angegeben. Die Mindest- und Maximalwerte werden wie bei Golden Search für alle erklärenden Variablen übernommen. Die geschätzte Anzahl der Nachbarn oder das Entfernungsband können jedoch für jede erklärende Variable unterschiedlich sein (sofern nicht zwei oder mehr Variablen denselben räumlichen Maßstab aufweisen). Die Ergebnisse der Schätzung der Nachbarschaften mit dieser Option sind mit denen von Golden Search vergleichbar. Allerdings ist diese Option schneller und kommt mit signifikant weniger Speicherauslastung aus.

• Manuelle Intervalle: Bestimmt die Anzahl der Nachbarn oder das Entfernungsband für jede erklärende Variable, indem die Anzahl der Nachbarn oder das Entfernungsband ausgehend von einem Minimalwert inkrementiert wird. Für die Option "Anzahl der Nachbarn" beginnt die Methode mit dem Wert des Parameters Minimale Anzahl von Nachbarn. Die Anzahl der Nachbarn wird dann um den Wert des Parameters Inkrement für die Anzahl der Nachbarn erhöht. Dieses Inkrement wird so viele Male wiederholt, wie im Parameter Anzahl von Inkrementen angegeben. Für die Option "Entfernungsband" verwendet die Methode die Parameter Minimale Suchentfernung, Inkrement für die Suchentfernung und Anzahl von Inkrementen. Die Anzahl der Nachbarn oder das Entfernungsband, die bzw. das von jeder erklärenden Variablen verwendet wird, ist einer der getesteten Werte, aber die Werte können für jede erklärende Variable unterschiedlich sein. Diese Option ist schneller als die Option "Golden Search" und wird häufig zur Schätzung vergleichbarer Nachbarschaften genutzt.

• Benutzerdefiniert: Die Anzahl der Nachbarn oder das Entfernungsband, die bzw. das von allen erklärenden Variablen verwendet wird. Der Wert wird mit dem Parameter Anzahl der Nachbarn bzw. Entfernungsband angegeben. Diese Option bietet die größte Kontrolle, wenn Sie die optimalen Werte kennen.

Standardmäßig werden die abhängigen Nachbarschaftsparameter jeder Auswahlmethode für Nachbarschaften auf alle erklärenden Variablen angewendet. Es können jedoch nur für bestimmte erklärende Variablen angepasste Parameter für die Auswahl der Nachbarschaft mit dem entsprechenden Override-Parameter für den Nachbarschaftstyp und die Auswahlmethode angegeben werden: Anzahl der Nachbarn für Golden Search, Anzahl der Nachbarn für Gradientensuche, Anzahl der Nachbarn für manuelle Intervalle, Benutzerdefinierte Anzahl der Nachbarn, Suchentfernung für Golden Search, Suchentfernung für Gradientensuche, Suchentfernung für manuelle Intervalle oder Benutzerdefinierte Suchentfernung. Um angepasste Nachbarschaften für bestimmte erklärende Variablen zu verwenden, geben Sie die erklärenden Variablen in der ersten Spalte des entsprechenden Override-Parameters und die angepassten Optionen der Nachbarschaft in den anderen Spalten an. Die Spalten haben dieselben Namen wie die Parameter, die sie überschreiben. Wenn Sie beispielsweise manuelle Intervalle mit Entfernungsband verwenden, enthält die Spalte Inkrement für die Suchentfernung angepasste Werte des Parameters Inkrement für die Suchentfernung. Im Bereich Geoverarbeitung befinden sich die angepassten Nachbarschaftsparameter in der Parameterkategorie Optionen für angepasste Nachbarschaften.

Angenommen, Sie verwenden drei erklärende Variablen mit dem Nachbarschaftstyp "Golden Search" mit einer minimalen Anzahl von 30 und einer maximalen Anzahl von 40 Nachbarn. Wenn das Werkzeug mit diesen Parametern ausgeführt wird, verwendet jede der drei erklärenden Variablen zwischen 30 und 40 Nachbarn. Wenn Sie stattdessen nur für die zweite erklärende Variable zwischen 45 und 55 Nachbarn verwenden möchten, können Sie die zweite erklärende Variable, das angepasste Minimum und das angepasste Maximum in den Spalten des Parameters Anzahl der Nachbarn für Golden Search angeben. Mit diesen Parametern verwenden die erste und die dritte erklärende Variable zwischen 30 und 40 Nachbarn, und die zweite erklärende Variable verwendet zwischen 45 und 55 Nachbarn.

Lokales Gewichtungsschema

MGWR schätzt für jedes Ziel-Feature ein lokales Regressionsmodell, indem eine geographische Gewichtungsfunktion (Kernel-Funktion) auf das Feature und dessen benachbarte Features angewendet wird. Nachbarn, die sich näher am Ziel-Feature befinden, haben einen größeren Einfluss auf das lokale Modell. Die Kernel-Optionen sind im Parameter Lokales Gewichtungsschema verfügbar: Gauß und Biquadrat. Weitere Informationen zur geographischen Gewichtung mit Kerneln finden Sie unter Funktionsweise des Werkzeugs "Geographisch gewichtete Regression". In MGWR variiert die Gewichtungsbandbreite der erklärenden Variablen.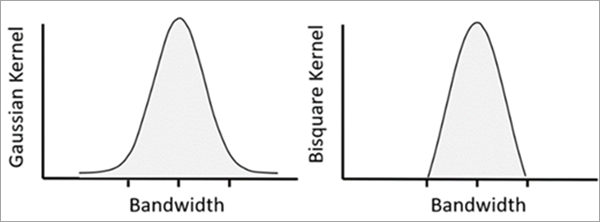

Hinweis:

Beim Nachbarschaftstyp für die Gradientensuche ist nur der Biquadrat-Kernel zulässig. Der Gauß-Kernel könnte in künftigen Versionen zulässig sein.

Skalierte Daten und Koeffizienten

Standardmäßig werden alle erklärenden Variablen und die abhängige Variable skaliert, sodass sie einen Mittelwert von null und eine Standardabweichung von eins aufweisen (wird auch als Z-Wert-Standardisierung bezeichnet). Die geschätzten Koeffizienten der skalierten Datenwerte werden in Standardabweichungen interpretiert. Beispielsweise bedeutet der Koeffizient 1,2, dass eine Zunahme der Standardabweichung von 1 in der erklärenden Variablen mit einer Zunahme der Standardabweichung von 1,2 der abhängigen Variablen korreliert. Da alle Koeffizienten eine gemeinsame Einheit verwenden, können die Werte direkt verglichen werden, um festzustellen, welche erklärenden Variablen den größten Einfluss auf das Modell haben. Im Allgemeinen ist es empfehlenswert, die Variablen zu skalieren. Die Skalierung ist besonders wichtig, wenn der Wertebereich der Variablen erheblich variiert. Sie können jedoch festlegen, dass die Daten nicht skaliert werden, indem Sie den Parameter Daten skalieren deaktivieren.

Bei den meisten linearen Regressionsmodellen wie OLS und GWR bleiben die Koeffizienten bei linearer Skalierung unverändert. Wenn Sie also die Eingabedaten skalieren, das Regressionsmodell anpassen und dann das Ergebnis wieder zurück in die Originaleinheiten skalieren, ist das Ergebnis so, als ob Sie keine Skalierung vorgenommen hätten. In MGWR führt die Skalierung und deren anschließende Umkehr nicht zu dem Modell, dass Sie mit den Originaldaten erhalten würden. Die Ursache ist, dass das Backfitting ein iteratives Verfahren ist, bei dem die Ergebnisse der einzelnen Schritte von den Ergebnissen der vorherigen Schritte abhängen. Die Verwendung unterschiedlicher Anfangsmaßstäbe hat Einfluss auf den Pfad der getesteten Werte und führt zu eindeutigen MGWR-Modellen. Die skalierten Ergebnisse sind normalerweise genauer, da durch die Skalierung Varianzen der Variablen ausgeglichen werden. Zudem konvergiert das iterative Verfahren in der Regel schneller und in genauere Werte, wenn die einzelnen Variablen gleiche Beträge zur Gesamtvarianz der Daten beitragen. Wenn die erklärenden Variablen unterschiedliche Varianzen aufweisen (da sie zum Beispiel verschiedene Einheiten haben), haben die Variablen mit größeren Varianzen mehr Einfluss auf die einzelnen Schritte der iterativen Schätzung. In den meisten Fällen hat dieser Einfluss negative Auswirkungen auf die endgültigen Bandbreiten und Koeffizienten für das Modell.

Zur leichteren Interpretation der skalierten Ergebnisse enthalten alle Koeffizienten der Werkzeugausgaben einen skalierten Wert und den nicht skalierten Wert in den Originaldateneinheiten. Diese Ausgaben umfassen zusätzliche Felder für die Ausgabe-Features (die auch als Layer zum Ausgabe-Gruppen-Layer hinzugefügt werden) und zusätzliche Raster im Verzeichnis des Parameters Ausgabe-Koeffizienten-Raster-Workspace. Beim Vorhersagen neuer Positionen mit den Parametern Vorhersage-Positionen und Ausgabe-Vorhersage-Features sind alle vorhergesagten Werte nicht skaliert in den Originaldateneinheiten. Weitere Informationen zu den Ausgaben finden Sie unter Werkzeugausgaben.

Werkzeugausgaben

Das Werkzeug erzeugt eine Vielzahl unterschiedlicher Ausgaben, darunter einen Gruppen-Layer für verschiedene Felder der Ausgabe-Features, Meldungen und Diagramme. Zu den optionalen Ausgaben gehört eine Feature-Class, die Werte an neuen Positionen vorhersagt, eine Nachbarschaftstabelle und Raster-Oberflächen der einzelnen Koeffizienten.

Gruppen-Layer und Symbolisierung

Der standardmäßige Ausgabe-Symbolisierungs-Layer visualisiert die standardisierten Residuen der lokalen linearen Regressionsmodelle mit einem klassifizierten Farbschema. Untersuchen Sie die Muster der Residuen, um festzustellen, ob das Modell richtig angegeben wurde. Residuen für richtig angegebene Regressionsmodelle sind normal und räumlich zufällig verteilt, ohne Cluster-Bildung der Werte. Sie können das Werkzeug Räumliche Autokorrelation (Global Moran's I) für die Residuen der Regression verwenden, um zu testen, ob sie räumlich zufällig sind. Statistisch signifikante hohe oder geringe Cluster-Bildung der Residuen ist ein Indikator für ein nicht optimales MGWR-Modell.

Der Karte werden Layer der Koeffizienten- und der statistischen Signifikanz jeder erklärenden Variable als Gruppen-Layer mit separaten Untergruppen-Layern für jede erklärende Variable hinzugefügt. Jeder Koeffizienten-Layer zeigt ein divergierendes Farbschema an, dass bei null zentriert ist. Dadurch können Sie anhand der Farbe bestimmen, welche Variablen positive und negative Beziehungen zur abhängigen Variablen haben. Für Punkte werden statistisch signifikante Features (95 Prozent Konfidenz) durch grüne Halos um die Punkte und nicht signifikante Beziehungen durch graue Halos angegeben. Für Polygone werden signifikante Beziehungen mit texturierten Meshes in den Polygonen angegeben. Untersuchen Sie die Koeffizienten-Layer und die Signifikanz-Layer, um die räumliche Variation in den erklärenden Variablen besser zu verstehen. Sie können Ihre Erkenntnisse aus dieser räumlichen Variation auch für Richtlinien verwenden. Globale Richtlinien können gut funktionieren, wenn Variablen global statistisch signifikant sind und nur eine geringe regionale Variation aufweisen. Bei substanzieller räumlicher Variation in den Regressionskoeffizienten können dagegen lokale Richtlinien besser geeignet sein. In diesem Fall kann es sinnvoll sein, Richtlinien in Gebieten, in denen der lokale Effekt positiv und groß ist, zu aktivieren. Dieselben Richtlinien können aber in Gebieten, in denen der lokale Effekt klein oder negativ ist, ungeeignet sein.

Meldungen und Diagnosen

Die Meldungen bieten Informationen zum MGWR-Modell und dessen Performance. Die Meldungen bestehen aus mehreren Abschnitten.

Summenstatistik für Koeffizienten-Schätzungen

Der Abschnitt Summenstatistik für Koeffizienten-Schätzungen fasst Mittelwert, Standardabweichung, Minimum, Medianwert und Maximum der Koeffizienten-Schätzungen für das Untersuchungsgebiet zusammen. Der Mittelwert für jeden Koeffizienten stellt den Zusammenhang zwischen dieser erklärenden Variablen und der abhängigen Variablen dar. Die Standardabweichung gibt die räumliche Variation für die einzelnen erklärenden Variablen an. Eine kleine Standardabweichung bedeutet, dass zum Modellieren der Daten eine einfachere Methode, wie zum Beispiel OLS, besser geeignet sein könnte. Wenn der Parameter Daten skalieren aktiviert ist, können Sie die Werte von erklärenden Variablen vergleichen. Wenn der Parameter Daten skalieren nicht aktiviert ist, kann der Wert von Koeffizienten zwischen erklärenden Variablen nicht direkt verglichen werden, da sich die Einheiten unterscheiden können.

Modelldiagnose

Der Abschnitt Modelldiagnose enthält eine Tabelle, in der verschiedene Modelldiagnosen für GWR und MGWR aufgeführt sind, einschließlich R²-Wert, angepasster R²-Wert, AICc, Residuenvarianz und die Anzahl von effektiven Freiheitsgraden. Weitere Details zu diesen Modelldiagnosen finden Sie unter Funktionsweise des Werkzeugs "Geographisch gewichtete Regression".

Hinweis:

In einigen Fällen kann das GWR-Modell für Vergleiche möglicherweise nicht berechnet werden. In diesem Fall wird nur die Diagnose für MGWR angezeigt.

Sie können mit den R²- und angepassten R²-Diagnosen die Eignung des Modells für die Daten bewerten. Je höher der R2- und der angepasste R2-Wert sind, desto besser passt das Modell zu den Daten. Bewerten Sie die Komplexität des Modells anhand der Anzahl der erklärenden Variablen und der Diagnose "Effektive Freiheitsgrade". Einfachere Modelle haben einen höheren effektiven Freiheitsgrad und weniger Parameter. Wenn ein Modell zu viele Parameter aufweist, besteht das Risiko einer Überanpassung der Daten. Die AICc-Diagnose berücksichtigt die Eignung und die Komplexität des Modells. Das Werkzeug Geographisch gewichtete Regression (Multiscale) wählt das Modell mit dem niedrigsten AICc aus.

Zusammenfassung der erklärenden Variablen und Wohnquartiere

Der Abschnitt Zusammenfassung der erklärenden Variablen und Wohnquartiere zeigt die geschätzten Nachbarschafts- und Signifikanzniveaus für die einzelnen erklärenden Variablen an. Für Nachbarschaften, die auf einer Anzahl von Nachbarn basieren, wird die optimale Anzahl von Nachbarn als Anzahl und als Prozentsatz der Gesamtzahl der Eingabe-Features dargestellt. Beim Nachbarschaftstyp "Entfernungsband" werden die optimalen Entfernungsbänder zusammen mit der Entfernung als Prozentsatz der diagonalen Ausdehnung der Eingabe-Features dargestellt. Die Prozentsätze für Feature oder Ausdehnung sind zur Charakterisierung des räumlichen Maßstabs der erklärenden Variablen nützlich. Wenn eine erklärende Variable z. B. 75 Prozent der Features als Nachbarn verwendet, sind die lokalen Regressionsmodelle näher an globalen Modellen als an lokalen Modellen (was darauf hinweist, dass ein einfacheres Modell, wie zum Beispiel OLS, besser geeignet sein könnte). Wenn eine andere erklärende Variable nur 5 Prozent der Eingabe-Features als Nachbarn nutzt, ist es ein eher lokales Modell. Für alle Nachbarschaftstypen werden die Anzahl und der Prozentsatz lokaler Modelle, die bei einem Konfidenzniveau von 95 Prozent statistisch signifikant waren, für jede erklärende Variable angezeigt.

Optimaler Bandbreiten-Suchverlauf

Im Abschnitt Optimaler Bandbreiten-Suchverlauf wird der Suchverlauf potenziell optimaler Bandbreiten entlang des AICc-Wertes für jeden Satz getesteter Werte angezeigt. Das Werkzeug beginnt die Suche nach der optimalen Bandbreite für jede erklärende Variable, indem jeder Variablen der gleiche Wert zugewiesen wird: die optimale Bandbreite von GWR. Dann passt das Werkzeug die Bandbreite und den Koeffizienten für jede Variable bei jeder Iteration an und schätzt einen neuen AICc-Wert. Mit dem Fortschreiten der Iterationen nimmt der AICc-Wert ab, bis er sich stabilisiert, oder er nimmt zu, womit die Iterationen enden. Für die Option Benutzerdefiniert sind normalerweise die wenigsten Iterationen erforderlich, für die Option Golden Search dagegen die meisten. Obwohl bei der Option Gradientensuche eine große Anzahl von Iterationen verwendet werden, erfolgt bei ihr in der Regel die Ausführung am schnellsten, da jede Iteration schnell berechnet werden kann.

Hinweis:

Bei der Gradientensuche mit Anzahl der Nachbarn weicht der endgültige AICc-Wert, der im Abschnitt mit dem optimalen Bandbreiten-Suchverlauf angezeigt wird, häufig leicht von dem AICc-Wert, der im Abschnitt mit den Modelldiagnosen angezeigt wird, ab. Der Grund dafür besteht darin, dass bei der Gradientensuche eine kontinuierliche Darstellung der Anzahl der Nachbarn während der Bandbreitenoptimierung verwendet wird, was zu einer geringfügigen Ungenauigkeit im berechneten AICc-Wert jeder Iteration führt. Wenn der AICc-Wert des endgültigen Modells in Berichten verwendet werden soll, dann verwenden Sie dafür den Wert, der im Abschnitt mit den Modelldiagnosen angezeigt wird.

Zusammenfassung der Bandbreitenstatistik

Der Abschnitt Zusammenfassung der Bandbreitenstatistik fasst die Werte zusammen, mit denen getestet wird, ob jede erklärende Variable in jedem lokalen Modell statistisch signifikant ist. Zu diesen Statistiken gehören die optimale Nachbarschaft (Anzahl der Nachbarn oder Entfernungsband) von MGWR, die effektive Anzahl von Parametern, das angepasste Signifikanzniveau (Alpha) und der angepasste kritische Wert von Pseudo-t-Statistiken. Mit diesen Werten werden die Felder im Zusammenhang mit der statistischen Signifikanz für jede erklärende Variable in den Ausgabe-Features erstellt. Der angepasste Alpha-Wert wird berechnet, indem das Signifikanzniveau (0,5) durch die effektive Anzahl von Parametern geteilt wird. Damit wird die familienweise Fehlerrate (FWER) der Signifikanz der erklärenden Variablen gesteuert. Der angepasste Alpha-Wert wird als Signifikanzniveau in einem zweiseitigen t-Test mit der effektiven Anzahl von Freiheitsgraden verwendet.

Ausgabe-Features

Das Werkzeug gibt eine Feature-Class aus, die lokale Diagnosen für jedes Feature enthält. Zu den Diagnosen gehören folgende: Regressionsresiduen, standardisierte Residuen, vorhergesagte Werte der abhängigen Variablen, Schnittpunkt, Koeffizienten von erklärenden Variablen, Standardfehler von Koeffizienten, Pseudo-t-Statistiken von Koeffizienten, Koeffizientensignifikanz, Einfluss, Cook'sche Distanz, lokaler R2-Wert und Bedingungswert. Weitere Details zu diesen Diagnosen finden Sie unter Funktionsweise des Werkzeugs "Geographisch gewichtete Regression".

Diagramme

Dem Bereich Inhalt werden die folgenden Diagramme hinzugefügt:

• Beziehung zwischen Variablen: Eine Scatterplotmatrix mit 1 abhängigen Variable und bis zu 9 erklärenden Variablen, die die Korrelation zwischen der abhängigen Variable und jeder erklärenden Variable und die Korrelation zwischen jedem Paar erklärender Variablen zeigt. Starke Korrelationen zwischen einem Paar kennzeichnen Multikollinearität.
• Verteilung von standardisiertem Residuum: Ein Histogramm der standardisierten Residuen. Die standardisierten Residuen sollten normal verteilt sein und einen Mittelwert von null sowie eine Standardabweichung von eins aufweisen
• Standardisiertes Residuum und vorausgesagtes Plot: Ein Scatterplot zwischen den standardisierten Residuen und deren entsprechenden vorausgesagten Werten. Das Diagramm sollte dem Zufallsprinzip folgen und keine Muster oder Trends darstellen.

Optionale Ausgaben

Die folgenden optionalen Ausgaben können in den Dropdown-Menüs Vorhersageoptionen und Zusätzliche Optionen angegeben werden.

• Der Parameterwert Vorhergesagte Ausgabe-Features ist eine Feature-Class mit Vorhersagen für die abhängige Variable an den Positionen, die mit dem Parameter Vorhersage-Positionen angegeben wurden.
• Der Parameterwert Ausgabe-Nachbarschaftstabelle speichert eine Tabelle, die Werte der Abschnitte Summenstatistik für Koeffizienten-Schätzungen und Zusammenfassung der erklärenden Variablen und Wohnquartiere aus den Meldungen enthält.
• Der Parameter Koeffizienten-Raster-Workspace gibt einen Workspace an (Verzeichnis oder Geodatabase), in dem die Raster der Koeffizienten gespeichert werden. Diese Koeffizienten-Raster-Oberflächen können eine Erklärung der räumlichen Variation in den Koeffizienten enthalten.

Multikollinearität

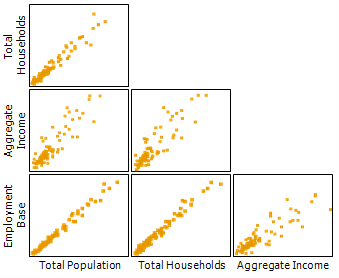
Multikollinearität tritt auf, wenn zwei oder mehr erklärende Variablen in einem Regressionsmodell eng korrelieren. Dies ist in OLS-, GLR-, GWR- und MGWR-Modellen möglich. Wenn die erklärenden Variablen korrelieren, haben sie gemeinsame Transinformationen. Das Regressionsmodell kann nicht zwischen den Effekten der Variablen unterscheiden, daher kann Multikollinearität einen negativen Einfluss auf die Schätzung der Koeffizienten und optimalen Nachbarschaften haben. In moderaten Fällen können die geschätzten Koeffizientenschätzungen verzerrt sein und eine große Unsicherheit aufweisen. In extremen Fällen kann das Modell möglicherweise nicht berechnet werden. Das folgende Beispiel zeigt eine Scatterplotmatrix von drei Variablen, die eng miteinander korrelieren, und in einem Regressionsmodell, in dem sie verwendet werden, treten wahrscheinlich Probleme mit der Multikollinearität auf.

Jedes Paar von Variablen weist eine enge Korrelation auf.

Identifizierung und Verhinderung von Multikollinearität in MGWR

In einem MGWR-Modell kann Multikollinearität in verschiedenen Situationen auftreten:

• Eine der erklärenden Variablen ist stark räumlich geclustert. Da MGWR lokale Regressionsmodelle anpasst, tritt wahrscheinlich eine Multikollinearität auf, wenn ein Feature und alle seine Nachbarn ungefähr denselben Wert für eine erklärende Variable haben.

  Um dies zu verhindern, stellen Sie die einzelnen erklärenden Variablen dar, und identifizieren Sie die Variablen, die sehr wenige mögliche Werte aufweisen oder bei denen identische Variablen räumlich geclustert sind. Wenn Sie diese Typen von Variablen beobachten, entfernen Sie sie aus dem Modell, oder stellen Sie sie so dar, dass ihr Wertebereich vergrößert wird. Eine variable Anzahl von Schlafzimmern kann z. B. besser dargestellt werden als Schlafzimmer pro Quadratfuß.

• Zwei oder mehr erklärende Variablen korrelieren global stark.

  Führen Sie ein globales Modell mit Generalisierte lineare Regression aus, und untersuchen Sie den Varianzinflationsfaktor (VIF) auf die einzelnen erklärenden Variablen. Wenn die VIF-Werte groß sind, beispielsweise 7,5 oder höher, wird MGWR möglicherweise aufgrund globaler Multikollinearität nicht ausgeführt. In diesem Fall sind die Variablen redundant. Sie könnten also eine dieser Variablen aus dem Modell entfernen oder mit anderen erklärenden Variablen kombinieren, um die Variation in den Werten zu vergrößern.

• Die definierte Nachbarschaft ist zu klein.

  Multikollinearität kann auch mehrere erklärende Variablen gleichzeitig betreffen. Dazu kommt es, wenn zwischen linearen Kombinationen einiger erklärender Variablen und linearen Kombinationen anderer erklärender Variablen eine hohe Korrelation besteht. Am häufigsten ist dies bei Nachbarschaften mit einer geringen Anzahl der Nachbarn der Fall. Um dies zu testen, überprüfen Sie den lokalen Bedingungswert in der Ausgabe-Feature-Class. Ein hoher lokaler Bedingungswert gibt an, dass die Ergebnisse aufgrund der lokalen Multikollinearität nicht stabil sind. Wenn dies der Fall ist, führen Sie das Modell mit einer größeren Anzahl von Nachbarn oder einem größeren Entfernungsband erneut aus. Bleiben Sie skeptisch bei Ergebnissen, in denen die Features einen Bedingungswert über 30 haben oder null sind. Bei Shapefiles werden NULL-Werte mit dem Wert -1,7976931348623158e+308 dargestellt. Der Bedingungswert ist an den Maßstab angepasst, um die Anzahl der erklärenden Variablen im Modell zu korrigieren. Dadurch können Sie den Bedingungswert zwischen Modellen, in denen eine andere Anzahl von erklärenden Variablen verwendet wird, direkt vergleichen.

Das Überprüfen aller dieser Bedingungen kann bei Problemen mit Multikollinearität helfen, sie aber nicht immer lösen.

Koeffizienten- und Bandbreitenschätzung

Bei allen Methoden zur Auswahl der Nachbarschaft mit Ausnahme der Gradientensuche werden die Koeffizienten und Bandbreiten durch einen Prozess geschätzt, der als "Backfitting" (Breiman et al. 1985) bezeichnet wird. Das Verfahren wurde ursprünglich zum Schätzen der Parameter von generalisierten additiven Modellen entwickelt. Es bewegt sich nacheinander durch die erklärenden Variablen und verwendet eine Glättungsfunktion, um den Koeffizienten zu kalibrieren, während alle anderen erklärenden Variablen konstant bleiben. Dieser Prozess wird für die erklärenden Variablen wiederholt, bis sich die Werte der Koeffizienten stabilisieren und sich nach einer anschließenden Iteration nicht ändern.

Bei der Anwendung auf MGWR (Fotheringham et al. 2017) ist die Glättungsfunktion ein univariates GWR-Modell, dass die vorherige mit Residuen angepasste Vorhersage mit der einzelnen erklärenden Variablen zurückentwickelt (wobei alle anderen erklärenden Variablen als Konstanten behandelt werden). Das GWR-Modell nutzt die gleiche Auswahlmethode für Nachbarschaften (Golden Search, manuelle Intervalle oder benutzerdefiniert), um den räumlichen Maßstab der erklärenden Variablen zu schätzen. Im Abschnitt Zusätzliche Quellen finden Sie eine vollständige Beschreibung des Prozesses.

Der Backfitting-Algorithmus muss mit initialisierten Werten der Koeffizienten beginnen. Diese Anfangswerte werden von einem GWR-Modell aller erklärenden Variablen geschätzt. Bei einem Modellfehler aufgrund von Multikollinearität wird stattdessen OLS verwendet. Wenn der Prozess nach 25 Iterationen nicht konvergiert, werden die Koeffizientenwerte der letzten Iteration verwendet.

Gradientensuche

Die Gradientensuche ist eine Methode zur Auswahl der Nachbarschaft, die einen jüngeren Ansatz zum Schätzen der optimalen Bandbreiten in MGWR ohne Rückanpassung ("Backfitting") darstellt. Die Hauptvorteile der Gradientensuche sind die schnellere Ausführung und die effiziente Speicherauslastung. Diese Methode ist ein Optimierungsalgorithmus zweiter Ordnung, der die Gradienten- und Hesse-Matrix verwendet, um den AICc-Wert in Bezug auf den räumlichen Maßstab der erklärenden Variablen zu minimieren. Anstatt in jedem iterativen Schritt den Parameter einer einzelnen erklärenden Variable zu aktualisieren, werden durch Absteigen in der steilsten Richtung des Gradienten, der durch die Krümmung des AICc korrigiert wird, die Parameter aller erklärenden Variablen gleichzeitig aktualisiert.

Die Ergebnisse von Golden Search und der Gradientensuche sind in der Regel sehr ähnlich. Die folgende Abbildung zeigt die tatsächliche Koeffizientenoberfläche zusammen mit der geschätzten Koeffizientenoberfläche bei Golden Search und der Gradientensuche. Wie Sie feststellen können, sind alle Oberflächen ähnlich und schätzen die tatsächliche Oberfläche genau.

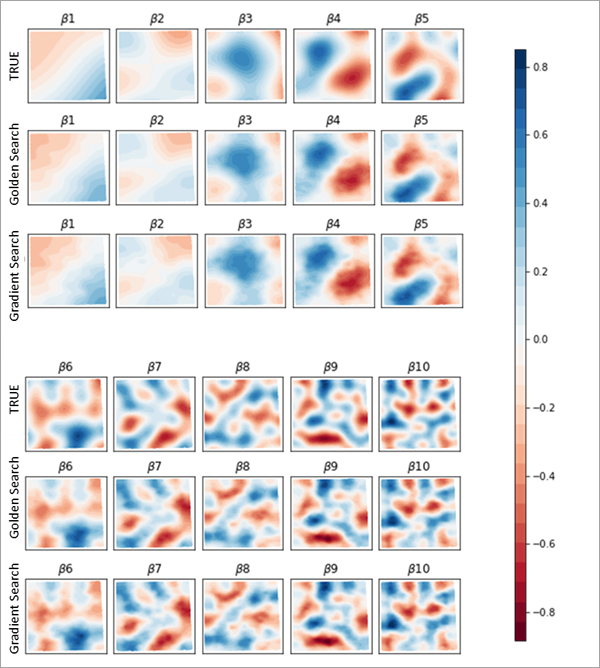
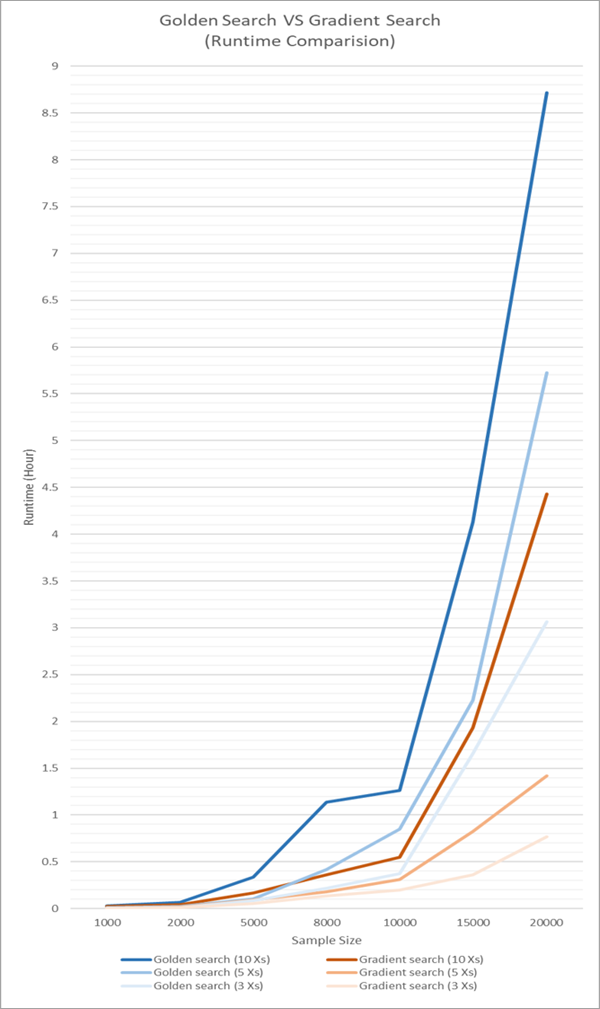
In der folgenden Abbildung werden die Laufzeiten bei Golden Search und der Gradientensuche für eine unterschiedliche Anzahl der erklärenden Variablen und unterschiedliche Dataset-Größen verglichen. Wie Sie feststellen können, ist bei derselben Anzahl der erklärenden Variablen die Laufzeit der Gradientensuche immer ungefähr halb so groß wie die Laufzeit von Golden Search.

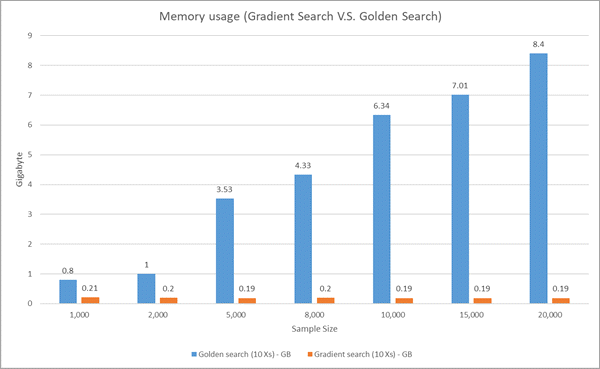
In der folgenden Abbildung wird die Speicherauslastung bei Golden Search und der Gradientensuche verglichen. Die Speicherauslastung bei Golden Search steigt mit zunehmender Stichprobengröße rapide an (quadratisches Wachstum), während die Speicherauslastung bei der Gradientensuche von der Stichprobengröße nicht beeinflusst wird.

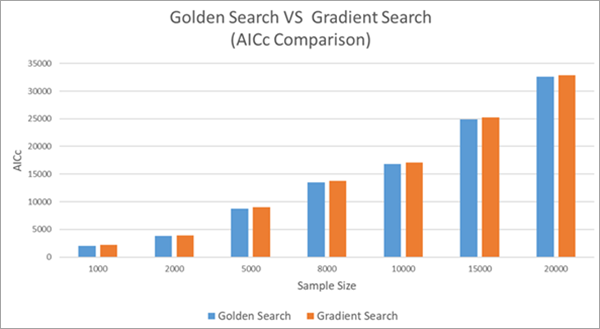
In der folgenden Abbildung werden die AICc-Werte bei Golden Search und der Gradientensuche verglichen. Zwar ist die Genauigkeit der Methoden sehr ähnlich, allerdings erreicht Golden Search etwas niedrigere AICc-Werte (was auf eine etwas genauere Schätzung hinweist) als die Gradientensuche.

Zusätzliche Quellen

Weitere Informationen finden Sie in den folgenden Ressourcen:

• Breiman, L., und J. H. Friedman. 1985 "Estimating optimal transformations for multiple regression and correlations" (mit Diskussion). Journal of the American Statistical Association 80, (391): 580–619. https://doi.org/10.2307/2288473. JSTOR 2288473.
• Brunsdon C., A. S. Fotheringham und M. E. Charlton. 1996. "Geographically weighted regression: A method for exploring spatial nonstationarity." Geographical Analysis 28: 281-298.
• Conn, A.R., N.I.M. Gould und P.L. Toint. 2000. "Trust Region Methods." Society for Industrial and Applied Mathematics. https://doi.org/10.1137/1.9780898719857.
• da Silva, A. R. und A. S. Fotheringham. 2016. "The multiple testing issue in geographically weighted regression." Geographical Analysis 48(3), 233–247. https://doi.org/10.1111/gean.12084.
• Fotheringham, A. S., W. Yang und W. Kang. 2017 "Multiscale geographically weighted regression (MGWR)." Annals of the American Association of Geographers 107: 1247–265. https://doi.org/10.1080/24694452.2017.1352480
• Oshan, T. M., Z. Li, W. Kang, L. J. Wolf und A. S. Fotheringham. 2019 "mgwr: A Python implementation of multiscale geographically weighted regression for investigating process spatial heterogeneity and scale". ISPRS International Journal of Geo-Information 8: 269.
• Yu, H., A. S. Fotheringham, Z. Li, T. Oshan, W. Kang und L. J. Wolf. 2020 "Inference in multiscale geographically weighted regression". Geographical Analysis 52: 87–106.
• Zhou, X., R. Assunção, H. Shao, M. Janikas, C. Huang und H. Asefaw. 2023. "Gradient-based optimization for Multi-scale Geographically Weighted Regression." (Wird überprüft)