Mit dem Werkzeug Erneut skalieren nach Funktion werden Eingabe-Raster-Werte anhand einer angegebenen Transformationsfunktion erneut skaliert. Es gibt eine Vielzahl von Transformationsfunktionen, deren Berechnungsmethode und Anwendung jeweils unterschiedlich sind. Welches Werkzeug verwendet wird, hängt davon ab, welche Funktion das untersuchte Phänomen am besten erfasst. Sie können die Eigenschaften der jeweiligen Funktion durch eine Reihe von Eingabeparametern weiter optimieren.
Um die Informationen in diesem Abschnitt bestmöglich nutzen zu können, ist es hilfreich, mit den für dieses Werkzeug grundlegenden Begriffen vertraut zu sein. Informationen dazu, wie sich die unteren und oberen Grenzwerte der Transformationsfunktion auf die Ausgabewerte auswirken, finden Sie unter Die Auswirkungen des unteren und oberen Grenzwertes auf die Ausgabewerte für "Erneut skalieren nach Funktion".
Liste der Funktionen
Die folgende Tabelle enthält eine Übersicht über die einzelnen Funktionen mit Links zu den jeweiligen Erläuterungen zu der Funktion.
Wird verwendet, wenn die Präferenz bei einer Erhöhung der Eingabewerte zunimmt, wobei die Präferenz schneller zunimmt als die Eingabewerte. | |
Wird verwendet, wenn die höchsten Präferenzen um einen bestimmten Eingabewert liegen, wobei die Präferenzen abnehmen, je weiter sich die Eingabewerte von diesem Wert entfernen. | |
Wird verwendet, um anzugeben, dass größere Eingabewerte eine höhere Präferenz haben. | |
Skaliert die Eingabewerte mithilfe einer linearen Funktion erneut. | |
Wird verwendet, wenn die Präferenz für die niedrigen Eingabewerte sich schnell erhöht, wenn die Werte zunehmen, und die Präferenz dann bei einer weiteren Erhöhung der Eingabewerte sich kaum weiter ändert. | |
Wird verwendet, wenn kleine Eingabewerte die höchste Präferenz darstellen. Die Präferenzen nehmen mit zunehmenden Werten schnell ab, bis sie sich bei den höheren Eingabewerten kaum weiter ändern. | |
Wird verwendet, wenn große Eingabewerte die höchste Präferenz darstellen. Die Präferenzen nehmen mit zunehmenden Werten schnell zu, bis sie sich bei den größeren Eingabewerten kaum weiter ändern. | |
Skaliert die Eingabedaten auf Grundlage von Mittelwert und Standardabweichung erneut, wobei größere Werte im Eingabe-Raster als günstiger angesehen werden. | |
Skaliert die Eingabedaten auf Grundlage von Mittelwert und Standardabweichung erneut, wobei kleinere Werte im Eingabe-Raster als günstiger angesehen werden. | |
Wird verwendet, wenn die Eingabewerte, die sehr nah am Mittelpunkt liegen, als günstiger angesehen werden. | |
Wird verwendet, wenn die Präferenz der Eingabewerte bei einer Erhöhung der Eingabewerte schnell zunimmt. | |
Wird verwendet, um anzugeben, dass die kleineren Werte aus dem Eingabe-Raster als günstiger angesehen werden. | |
Wird verwendet, wenn ein bestimmter Eingabewert als am günstigsten angesehen wird, wobei die Präferenzen linear abnehmen, je weiter sich die Eingabewerte von diesem Punkt entfernen. |
Funktionsübersicht und -darstellung
Für jede Funktion werden eine allgemeine Übersicht, ein Anwendungsfall und Informationen zu den Auswirkungen bestimmter Eingabeparameter auf die Funktionskurve dargestellt.
Übersicht
In der Übersicht werden grundlegende Eigenschaften sowie spezifische Verhaltensweisen der einzelnen Funktionen beschrieben.
Anwendungsfall
Im Anwendungsfall wird ein spezifisches Beispiel beschrieben, für das die jeweilige Funktion sich gut eignet.
Auswirkungen der Parameter
In diesem Beispiel wird erläutert, wie sich die formbestimmenden Parameter auf die Funktion auswirken. Es wird beschrieben, wie sich eine Änderung des Parameterwertes auf die Kurve auswirkt. Diese Auswirkungen werden in einem Diagramm mit mehreren verschiedenen Werten für den dargestellten Parameter gezeigt. Außerdem wird ein Python-Klassenausdruck einbezogen und damit demonstriert, wie die in den Diagrammen angezeigte Transformationsfunktion erstellt wurde.
Hinweis:
Für jedes angezeigte Diagrammbeispiel ist die Eingabe ein Raster mit Werten zwischen 0 und 500. Es gibt keinen besonderen Grund für diese spezielle Auswahl, aber sie wird durchgängig verwendet, um Vergleiche zu erleichtern. In der Praxis können die tatsächlichen Eingabe-Raster einen beliebigen Bereich von Eingabewerten umfassen.
Funktion "Exponential"
Übersicht
Mit der Funktion Exponential werden die Eingabedaten transformiert, indem mithilfe eines bestimmten Versatz- und Basisfaktors eine Exponentialfunktion angewendet wird. In einem Eignungsmodell kann diese Funktion besonders sinnvoll eingesetzt werden, wenn Positionen mit niedrigen Eingabewerten am ungünstigsten sind, die Präferenzen für Zellenpositionen mit höheren Werten jedoch schnell zunehmen.
Anwendungsfall
Überlegen Sie, wie Sie die Entfernung von Wasserquellen in einem Eignungsmodell für Landschildkröten neu skalieren würden. Landschildkröten ziehen aufgrund ihrer eingeschränkten Mobilität Orte in der Nähe von Wasser vor. Die Präferenz für Orte, die sich weiter vom Wasser entfernt befinden, nimmt mit zunehmender Entfernung schnell ab.
Auswirkungen der Parameter
Eingabeversatz
Der Eingabeversatz ist der Wert, der von den Eingabewerten subtrahiert wird. Die Exponentialfunktion wird auf die verschobenen Eingabewerte angewendet, um die Funktionswerte zu bestimmen.
Basisfaktor
Der Parameter Basisfaktor bestimmt, wie steil die Exponentialfunktion steigt. Mit zunehmendem Basisfaktor steigt die Präferenz für die niedrigen Eingabewerte langsamer, wenn die Eingabewerte größer werden, bei den größeren Eingabewerten nimmt die Präferenz jedoch schnell zu. Eine Änderung dieses Parameters kann sinnvoll sein, wenn es sich um einen kleinen Eingabedatenbereich handelt (z. B. 0 bis 1) und Sie eine Exponentialkurve zwischen den minimalen und maximalen Werten beibehalten möchten.
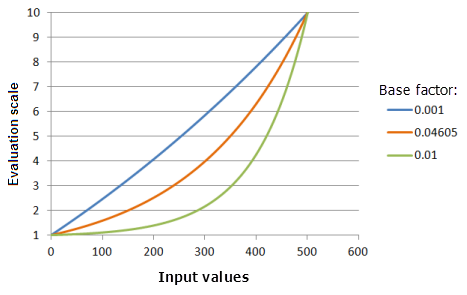
Verwendete Funktion im Schaubild oben:
- TfExponential(0.002651, BaseFactor, 0, 1, 500, 10)
Für BaseFactor werden folgende Werte verwendet: 0,001, 0,04605 und 0,01. Der Versatz um 0,002651 und der Basisfaktor von 0,04605 sind die standardmäßig berechneten Parameterwerte für das Eingabe-Dataset, das sich im Bereich 0 bis 500 befindet.
Funktion "Gauß'sche"
Übersicht
Bei der Funktion Gauß'sche werden die Eingabewerte mithilfe einer Normalverteilung transformiert. Beim Anwenden eines zunehmenden Auswertungsmaßstabs definiert der Mittelpunkt der Normalverteilung den Wert, der am günstigsten ist. Wenn sich der Mittelpunkt zwischen dem unteren und oberen Grenzwert befindet, wird dem Wert Bis-Maßstab ein Eingabewert zugewiesen, der dem Mittelpunkt entspricht. Die verbleibenden Eingabewerte nehmen auf dem Auswertungsmaßstab ab (absteigende Präferenz), je weiter die Werte in beiden Richtungen vom Mittelpunkt entfernt sind, bis sie den Wert Von-Maßstab erreichen. In einem Eignungsmodell ist diese Funktion am nützlichsten, wenn sich die höchste Präferenz in der Nähe eines bekannten Wertes befindet und die Präferenzen abnehmen, je weiter sich die Eingabewerte von diesem Wert entfernen.
Anwendungsfall
Bei der Installation von Solarkollektoren ist die Auswahl der richtigen Ausrichtung von großer Bedeutung für die Optimierung der Ausgangsleistung. In der nördlichen Hemisphäre ist eine Ausrichtung nach Süden (180 Grad) am günstigsten. Je weiter die Ausrichtung dagegen in Richtung Osten oder Westen erfolgt, desto stärker nimmt die Präferenz ab. Eine Ausrichtung nach Norden ist am ungünstigsten.
Auswirkungen der Parameter
Mittelpunkt
Der Parameter Mittelpunkt gibt das Zentrum der Gauß'schen Kurve an. Es kann empfehlenswert sein, den Mittelpunkt der Funktion vom Datenmittelpunkt zu verschieben, wenn entweder die niedrigeren oder höheren Werte wichtiger oder unwichtiger sind. Ein zweiter Grund für eine Verschiebung des Mittelpunktes kann vorliegen, wenn die Funktion an Werte des Kriteriums außerhalb des Datenbereichs angepasst werden soll.
Der Mittelpunkt kann den Bereich der Eingabewerte bestimmen, über den sich die Funktionskurve erstreckt.
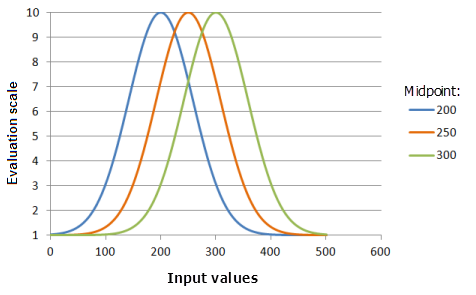
Verwendete Funktion im Schaubild oben:
- TfGaussian(Midpoint, 0.000147, 0, 1, 500, 10)
Für Midpoint) werden folgende Werte verwendet: 200, 250 und 300. Der Mittelpunkt 250 und die Spanne von 0,0000147 sind die standardmäßig berechneten Parameterwerte für das Eingabe-Dataset, das sich im Bereich 0 bis 500 befindet.
Spanne
Der Parameter Spanne bestimmt die Steilheit der Abnahme vom Mittelpunkt. Je größer der Wert, desto enger wird die Kurve um den Mittelpunkt (die Präferenz nimmt schneller ab).
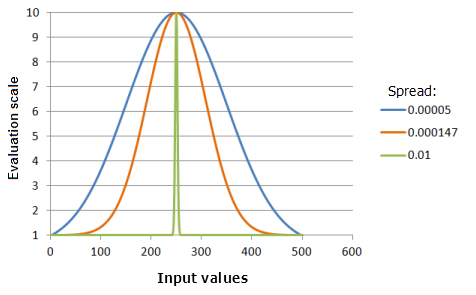
Verwendete Funktion im Schaubild oben:
- TfGaussian(250, Spread, 0, 1, 500, 10)
Für Spread werden folgende Werte verwendet: 0,00005, 0,000147 und 0,01. Der Mittelpunkt 250 und die Spanne von 0,0000147 sind die standardmäßig berechneten Parameterwerte für das Eingabe-Dataset, das sich im Bereich 0 bis 500 befindet.
Funktion "Groß"
Übersicht
Die Transformationsfunktion Groß wird verwendet, wenn die größeren Eingabewerte als günstiger angesehen werden. Der definierte Mittelpunkt bezeichnet den Übergangspunkt der Funktion. Werte, die höher Mittelpunkt sind, stellen eine abnehmende Präferenz dar, niedrigere Werte dagegen eine zunehmende Präferenz. Wie schnell die Werte mit zunehmendem Abstand vom Mittelpunkt zu- und abnehmen, wird durch den formbestimmenden Parameter Spanne festgelegt.
Anwendungsfall
Angenommen, Sie möchten ein Eignungsmodell für den Handel mit Bedarfsartikeln erstellen und dafür das Kriterium des Kaffeeertrags neu skalieren. Standorte mit einem höheren Ertrag haben eine höhere Präferenz, wobei die Präferenz mit dem Ertragswert nicht linear zunimmt.
Auswirkungen der Parameter
Mittelpunkt
Der Parameter Mittelpunkt bezeichnet den Übergangspunkt der Funktion. Wenn er auf einen Wert unter dem Mittelpunktwert der Eingabedaten verschoben wird, ändert sich der Übergangspunkt. Dies führt zu einer Zunahme der Präferenz im Bereich der größeren Werte rechts vom Mittelpunkt, wobei die Präferenz schneller steigt.
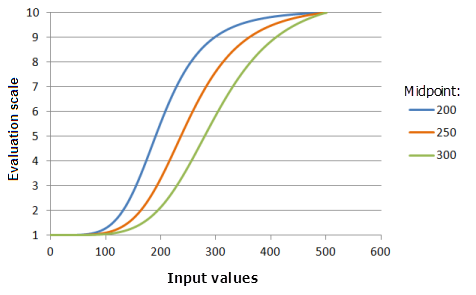
Verwendete Funktion im Schaubild oben:
- TfLarge(Midpoint, 5, 0, 1, 500, 10)
Für Midpoint werden folgende Werte verwendet: 200, 250 und 300. Der Mittelpunkt 250 und die Spanne von 5 sind die standardmäßigen Parameterwerte für das Eingabe-Dataset, das sich im Bereich 0 bis 500 befindet.
Spanne
Der Parameter Spanne legt fest, wie schnell die Präferenz zu- und abnimmt. Mit zunehmendem Spannenwert nimmt die Präferenz der Eingabewerte, die höher als der Mittelpunkt sind, gegen den oberen Grenzwert schneller zu, und die Eingabewerte, die niedriger als der Mittelpunkt sind, nehmen gegen den unteren Grenzwert schneller ab.
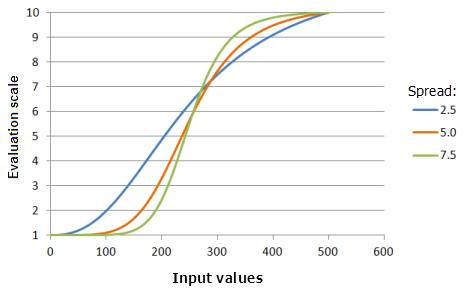
Verwendete Funktion im Schaubild oben:
- TfLarge(250, Spread, 0, 1, 500, 10)
Für Spread werden folgende Werte verwendet: 2,5, 5,0 und 7,5. Die Spanne 5 und der Mittelpunkt 250 sind die Standardparameterwerte für das Eingabe-Dataset, das sich im Bereich 0 bis 500 befindet.
Funktion "Linear"
Übersicht
Die Transformationsfunktion Linear wendet eine lineare Funktion auf die Werte zwischen dem angegebenen Minimum und Maximum an. Wenn der Von-Maßstab größer als der Bis-Maßstab ist, wird eine negative lineare Beziehung (eine negative Neigung) erstellt.
Diese Funktion ist besonders gut geeignet, wenn die Präferenzen für Werte in einem konstanten linearen Verhältnis zu- oder abnehmen.
Anwendungsfall
Angenommen, Sie möchten ein Eignungsmodell zum Klimawandel für die Lebensräume von Tieren erstellen und möchten dafür die Präferenz der Tiere für die Höhenwerte erneut skalieren. Innerhalb des Untersuchungsgebiets werden größere Höhenwerte als günstiger angesehen.
Auswirkungen der Parameter
Minimum
Der Parameter Minimum bestimmt den ersten Punkt, durch den die lineare Funktion führen muss. Es empfiehlt sich, als Parameterwert anstelle des Minimums der Eingabedaten einen Wert festzulegen, der der Präferenz des Phänomens für das Kriterium entspricht.
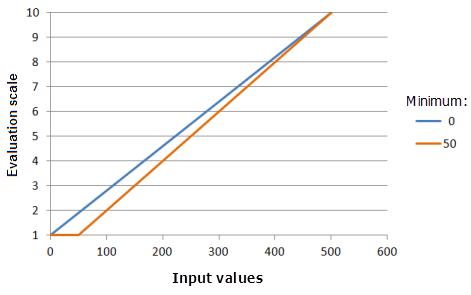
Verwendete Funktion im Schaubild oben:
- TfLinear(Minimum, 500, 0, 1, 500, 10)
Für Minimum werden folgende Werte verwendet: 0 und 50. Das Minimum 0 und das Maximum 500 sind die Standardparameterwerte für das Eingabe-Dataset, das sich im Bereich 0 bis 500 befindet.
Maximum
Der Parameter Maximum bestimmt den zweiten Punkt, durch den die lineare Funktion führen muss. Es empfiehlt sich, als Parameterwert anstelle des Maximums der Eingabedaten einen Wert festzulegen, der der Präferenz des Phänomens für das Kriterium entspricht.
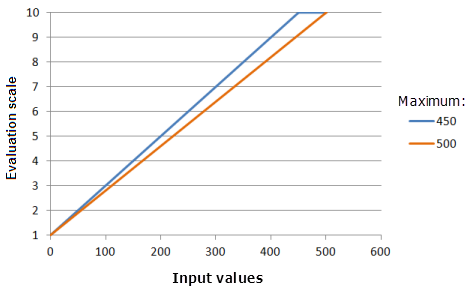
Verwendete Funktion im Schaubild oben:
- TfLinear(0, Maximum, 0, 1, 500, 10)
Für Maximum werden folgende Werte verwendet: 450 und 500. Das Minimum 0 und das Maximum 500 sind die Standardparameterwerte für das Eingabe-Dataset, das sich im Bereich 0 bis 500 befindet.
Funktion "Logarithmus"
Übersicht
Bei der Transformationsfunktion Logarithmus wird mithilfe eines bestimmten Versatzes und Faktors eine Logarithmusfunktion auf die Eingabedaten angewendet. In einem Eignungsmodell empfiehlt sich die Verwendung der Logarithmusfunktion, wenn die Präferenzen schnell zu- oder abnehmen und dann mit zunehmenden Eingabekriteriumswerten flach auslaufen.
Anwendungsfall
Angenommen, Sie möchten ein Eignungsmodell für Vögel erstellen und dafür das Kriterium Futtermenge neu skalieren. Die Präferenz für Orte mit wenig Futter ist am niedrigsten, wenn es zum Überleben der Vögel nicht ausreicht. Wenn das Futter zum Überleben ausreicht, nimmt die Präferenz für Orte mit höherer Futtermenge schnell zu, da die Vögel dadurch überlebensfähiger werden. Ab einem bestimmten Punkt steht den Vögeln genügend Futter zur Verfügung, sodass Orte mit noch größeren Futtermengen zwar wünschenswerter sind, jedoch in einem geringeren Maß.
Auswirkungen der Parameter
Verschieben
Der Wert Versatz wird von den Eingabewerten subtrahiert und kann den ersten Eingabewert für die Logarithmusberechnungen bestimmen. Im Anwendungsfall mit den Vögeln etwa sollte der Startpunkt für die Funktion zu 250 verschoben werden, wenn die Vögel an Orten mit weniger als 250 Futtereinheiten nicht leben können.
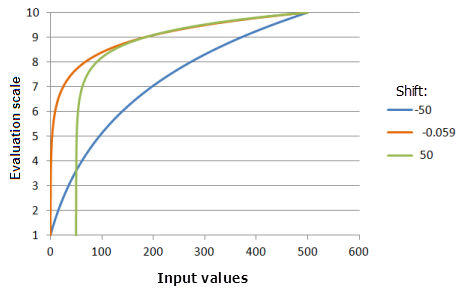
Verwendete Funktion im Schaubild oben:
- TfLogarithm(Shift, 0.0046, 0, 1, 500, 10)
Für Shift werden folgende Werte verwendet: -50,0, -0,059 und 50,0. Der Versatz um 0,059 und der Exponent 0,0046 sind die standardmäßig berechneten Parameterwerte für das Eingabe-Dataset, das sich im Bereich 0 bis 500 befindet.
Faktor
Der Faktor bezeichnet einen Multiplikator, der den Anstieg der Logarithmusfunktion steuert. Sie können diesen Parameter ändern, wenn es sich um einen kleinen Eingabewertebereich handelt (z. B. 0 bis 1), um die Logarithmuskurve zwischen dem minimalen und maximalen Wert beizubehalten.
Funktion "LogisticDecay"
Übersicht
Die Transformationsfunktion LogisticDecay entspricht einer logistischen Abnahmefunktion zwischen einem angegebenen Minimum und Maximum anhand eines definierten Y-Schnittpunktes in Prozent. In einem Eignungsmodell empfiehlt sich die Verwendung der logistischen Abnahmefunktion, wenn die niedrigen Eingabewerte am günstigsten sind. Mit steigenden Eingabewerten nehmen die Präferenzen schnell ab, bis die niedrigsten Präferenzen bei den hohen Eingabewerten sich nicht weiter verändern.
Anwendungsfall
Angenommen, Sie möchten ein Baueignungsmodell erstellen und die Entfernung von Elektroleitungen für das Kriterium Stromkosten neu skalieren. Die Standorte in der Nähe von Elektroleitungen werden als günstiger betrachtet, da der Anschluss an das Elektrizitätsnetz dort günstiger ist. Nach einer bestimmten Entfernung nehmen die Präferenzen schnell ab, da zusätzliche Transformatoren installiert werden müssten und damit zusätzliche Arbeits- und Materialkosten verbunden wären. Die Präferenz sinkt in den am weitesten entfernten Zellen nicht mehr weiter, da zusätzliche Kosten sich nicht mehr sehr auf die Präferenzen auswirken, weil die Standorte bereits zu teuer sind.
Auswirkungen der Parameter
Minimum
Der Parameter Minimum bestimmt den Startpunkt der logischen Abnahme. Je höher der Wert Minimum, desto schneller nimmt die Präferenz im Hauptteil der abnehmenden Funktion ab (die Kurve wird steiler).
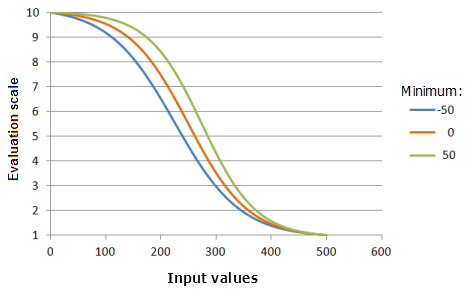
Verwendete Funktion im Schaubild oben:
- TfLogisticDecay(Minimum, 500, 99, 0, 1, 500, 10)
Für Minimum werden folgende Werte verwendet: -50, 0 und 50. Das Minimum 0 und das Maximum 500 sowie der Wert 99 für yInterceptPercent sind die Standardparameterwerte für das Eingabe-Dataset, das sich im Bereich 0 bis 500 befindet.
Maximum
Der Parameter Maximum bestimmt den Endpunkt der logistischen Abnahme. Je niedriger der Wert Maximum, desto schneller nimmt die Präferenz im Hauptteil der abnehmenden Funktion ab (die Kurve wird steiler).
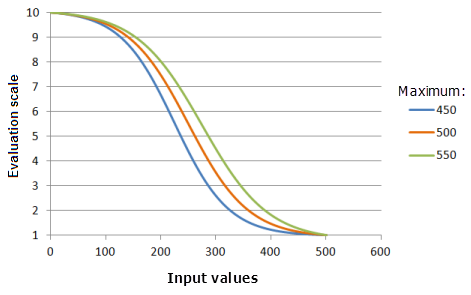
Verwendete Funktion im Schaubild oben:
- TfLogisticDecay(0, Maximum, 99, 0, 1, 500, 10)
Für Maximum werden folgende Werte verwendet: 450, 500 und 550. Das Minimum 0 und das Maximum 500 sowie der Wert 99 für yInterceptPercent sind die Standardparameterwerte für das Eingabe-Dataset, das sich im Bereich 0 bis 500 befindet.
Y-Schnittpunkt in Prozent
Der Parameter Y-Schnittpunkt in Prozent bestimmt den Wertebereich im Abnahmeteil der logistischen Abnahmekurve. Konzeptuell gesehen kann eine logistische Abnahmefunktion als umgekehrte S-Form visualisiert werden. Zwei auslaufende Enden werden durch den Hauptteil des "S" miteinander verbunden, der als Abnahmeteil der Kurve bezeichnet wird. Je größer der Wert für diesen Parameter, desto kleiner ist der Eingabewertebereich im Abnahmeteil der Kurve (das "S" ist aufrechter). Die Präferenz für die Werte nimmt jedoch schneller ab, und die Kurve ist ausgeprägter.
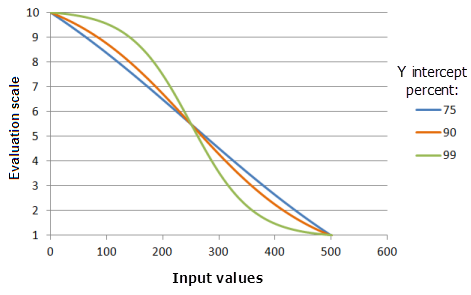
Verwendete Funktion im Schaubild oben:
- TfLogisticDecay(0, 500, YInterceptPercent, 0, 1, 500, 10)
Für den Y-Schnittpunkt in Prozent werden folgende Werte verwendet: 75, 90 und 99. Das Minimum 0 und das Maximum 500 sowie der Wert 99 für yInterceptPercent sind die Standardparameterwerte für das Eingabe-Dataset, das sich im Bereich 0 bis 500 befindet.
Funktion "LogisticGrowth"
Übersicht
Die Transformationsfunktion LogisticGrowth unterscheidet sich nur dadurch von der Transformationsfunktion "LogisticDecay", dass die Präferenzen in der logistischen Wachstumsfunktion zunehmen statt abnehmen.
Anwendungsfall
In einem Eignungsmodell zu Lebensräumen nehmen die Präferenzen eines Tieres mit zunehmender Verfügbarkeit von Futter logistisch zu. Die Futtermenge muss zuerst einen für das Überleben ausreichenden Wert erreichen, danach steigt die Präferenz mit zunehmendem Futter schnell an, bis die maximale Futteraufnahme erreicht wird. An diesem Punkt steigt die Präferenz nicht weiter.
Auswirkungen der Parameter
Minimum
Der Parameter Minimum bestimmt den Startpunkt des logischen Wachstums. Je höher der Wert Minimum, desto schneller nimmt die Präferenz im Hauptteil der steigenden Funktion zu (die Kurve wird steiler).
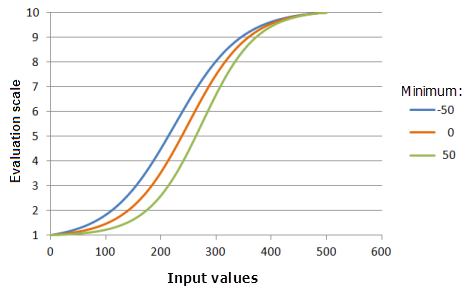
Verwendete Funktion im Schaubild oben:
- TfLogisticGrowth(Minimum, 500, 1, 0, 1, 500, 10)
Für Minimum werden folgende Werte verwendet: -50, 0 und 50. Das Minimum 0 und das Maximum 500 sowie der Wert 1 für yInterceptPercent sind die Standardparameterwerte für das Eingabe-Dataset, das sich im Bereich 0 bis 500 befindet.
Maximum
Der Parameter Maximum bestimmt den Endpunkt des logistischen Wachstums. Je niedriger der Wert Maximum, desto schneller nimmt die Präferenz im Hauptteil der wachsenden Funktion zu (die Kurve wird steiler).
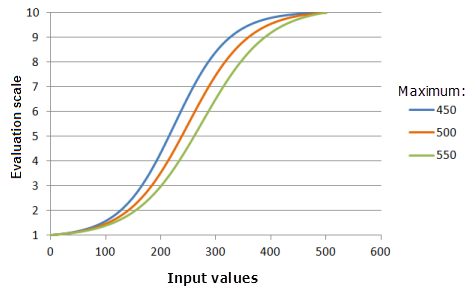
Verwendete Funktion im Schaubild oben:
- TfLogisticGrowth(0, Maximum, 1, 0, 1, 500, 10)
Für Maximum werden folgende Werte verwendet: 450, 500 und 550. Das Minimum 0 und das Maximum 500 sowie der Wert 1 für yInterceptPercent sind die standardmäßig berechneten Parameterwerte für das Eingabe-Dataset, das sich im Bereich 0 bis 500 befindet.
Y-Schnittpunkt in Prozent
Der Parameter Y-Schnittpunkt in Prozent bestimmt den Wertebereich im Abnahmeteil der logistischen Wachstumskurve. Konzeptuell gesehen kann eine logistische Wachstumsfunktion als S-Form visualisiert werden. Zwei auslaufende Enden werden durch den Hauptteil des "S" miteinander verbunden, der als Wachstumsteil der Kurve bezeichnet wird. Je kleiner der Wert yInterceptPercent, desto kleiner ist der Eingabewertebereich im Wachstumsteil der Kurve (das "S" ist aufrechter). Die Präferenz für die Werte nimmt jedoch schneller zu, und die Kurve ist ausgeprägter.
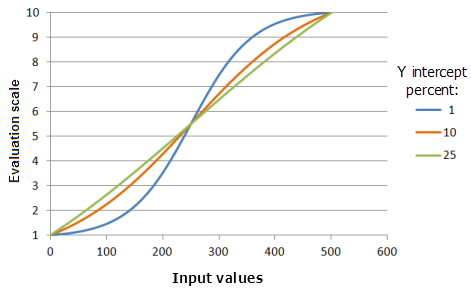
Verwendete Funktion im Schaubild oben:
- TfLogisticGrowth(0, 500, YInterceptPercent, 0, 1, 500, 10)
Für den Y-Schnittpunkt in Prozent werden folgende Werte verwendet: 1, 10 und 25. Das Minimum 0 und das Maximum 500 sowie der Wert 1 für yInterceptPercent sind die Standardparameterwerte für das Eingabe-Dataset, das sich im Bereich 0 bis 500 befindet.
Funktion "MSLarge"
Übersicht
Die Transformationsfunktion MSLarge unterscheidet sich nur dadurch von der Transformationsfunktion "Groß", dass die Definition der Funktion auf angegebenen Mittelwert- und Standardabweichungsmultiplikatoren beruht. Im Allgemeinen besteht der Unterschied darin, dass die Funktion "MSLarge" sich besser eignen kann, wenn die sehr großen Werte als günstiger angesehen werden.
Das Ergebnis kann abhängig von der Kombination der Mittelwert- und Standardabweichungsmultiplikatoren der Transformationsfunktion "Groß" ähnlich sein.
Anwendungsfall
Ähnlich dem Eignungsmodell für den Handel mit Bedarfsartikeln im Anwendungsfall für die Transformationsfunktion "Groß", die Standorte mit dem höheren Kaffeeertrag werden in diesem Fall jedoch als günstiger angesehen.
Auswirkungen der Parameter
Mittelwertmultiplikator
Der Parameter Mittelwertmultiplikator bestimmt die Neigung der Kurve der Funktion. Je mehr der Multiplikator abnimmt, desto mehr nimmt der geeignete Bereich der großen Werte zu, bis die Funktionskurve bei den hohen Werten zum oberen Grenzwert hin langsamer steigt.
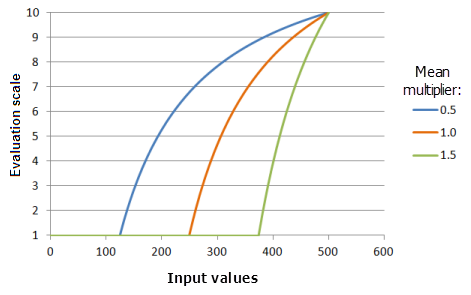
Verwendete Funktion im Schaubild oben:
- TfMSLarge(MeanMultiplier, 1, 0, 1, 500, 10)
Für den Mittelwert werden folgende Werte verwendet: 0,5, 1,0 und 1,5. Der Mittelwertmultiplikator 1 und der Standardabweichungsmultiplikator 1 sind die standardmäßig berechneten Parameterwerte für das Eingabe-Dataset, das sich im Bereich 0 bis 500 befindet.
Standardabweichungsmultiplikator
Der Parameter Standardabweichungsmultiplikator bestimmt die Neigung der Funktionskurve. Mit steigendem Multiplikator steigt die Funktionskurve immer langsamer.
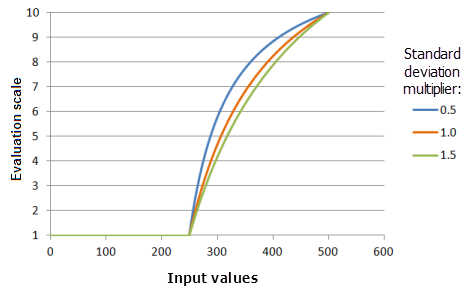
Verwendete Funktion im Schaubild oben:
- TfMSLarge(1, StandardDeviationMultiplier, 0, 1, 500, 10)
Für die Standardabweichung werden folgende Werte verwendet: 0,5, 1,0 und 1,5. Der Mittelwertmultiplikator 1 und der Standardabweichungsmultiplikator 1 sind die standardmäßig berechneten Parameterwerte für das Eingabe-Dataset, das sich im Bereich 0 bis 500 befindet.
Funktion "MSSmall"
Übersicht
Die Transformationsfunktion MSSmall unterscheidet sich nur dadurch von der Transformationsfunktion "Klein", dass die Definition der Funktion auf angegebenen Mittelwert- und Standardabweichungsmultiplikatoren beruht. Im Allgemeinen besteht der Unterschied darin, dass die Funktion "MSSmall" sich besser eignen kann, wenn die sehr kleinen Werte als günstiger angesehen werden.
Das Ergebnis kann abhängig von der Kombination der Mittelwert- und Standardabweichungsmultiplikatoren der Transformationsfunktion "Klein" ähnlich sein.
Anwendungsfall
Ähnlich wie die erneute Skalierung des Kriteriums der Entfernung von Straßen aufgrund der Baukosten im Baueignungsmodell, das für die Transformationsfunktion "Klein" erläutert wurde, die näheren Zellenstandorte werden in diesem Fall jedoch als günstiger angesehen.
Auswirkungen der Parameter
Mittelwertmultiplikator
Mittelwertmultiplikator: Bestimmt die Neigung der Funktionskurve. Je mehr der Multiplikator zunimmt, desto mehr nimmt der geeignete Bereich der kleinen Werte zu, bis die Funktionskurve bei den hohen Werten zum oberen Grenzwert hin schneller abnimmt.
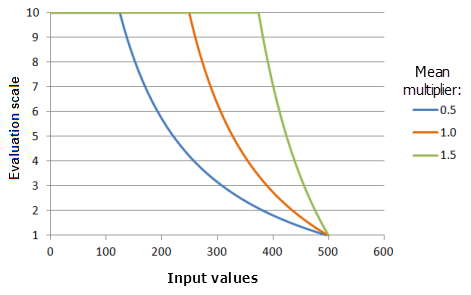
Verwendete Funktion im Schaubild oben:
- TfMSSmall(MeanMultiplier, 1, 0, 1, 500, 10)
Für den Mittelwert werden folgende Werte verwendet: 0,5, 1,0 und 1,5. Der Mittelwertmultiplikator 1 und der Standardabweichungsmultiplikator 1 sind die standardmäßig berechneten Parameterwerte für das Eingabe-Dataset, das sich im Bereich 0 bis 500 befindet.
Standardabweichungsmultiplikator
Der Parameter Standardabweichungsmultiplikator bestimmt die Neigung der Funktionskurve. Mit steigendem Multiplikator nimmt die Funktionskurve immer langsamer ab.
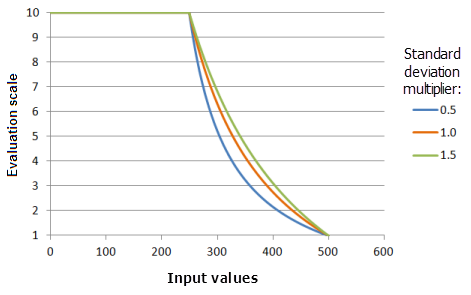
Verwendete Funktion im Schaubild oben:
- TfMSSmall(1, StandardDeviationMultiplier, 0, 1, 500, 10)
Für die Standardabweichung werden folgende Werte verwendet: 0,5, 1,0 und 1,5. Der Mittelwertmultiplikator 1 und der Standardabweichungsmultiplikator 1 sind die standardmäßig berechneten Parameterwerte für das Eingabe-Dataset, das sich im Bereich 0 bis 500 befindet.
Funktion "Nah"
Übersicht
Die Transformationsfunktion Nah ist am besten geeignet, wenn die höchste Präferenz in der Nähe eines bestimmten Wertes liegt. Wenn sich der Mittelpunkt zwischen dem unteren und oberen Grenzwert befindet, wird dem Wert Bis-Maßstab ein Eingabewert zugewiesen, der dem Mittelpunkt entspricht. Die verbleibenden Eingabewerte nehmen auf dem Auswertungsmaßstab ab (absteigende Präferenz), je weiter die Werte in beiden Richtungen vom Mittelpunkt entfernt sind, bis sie den Wert Von-Maßstab erreichen.
Die Transformationsfunktionen "Nah" und "Gauß'sche" können abhängig von den angegebenen Parametern ähnlich sein. Die Funktion "Nah" nimmt im Allgemeinen schneller und mit einer engeren Spanne als die Gauß'sche Funktion ab. Sie wird deshalb verwendet, wenn die Werte, die sehr nah am Mittelpunkt liegen, als günstiger angesehen werden.
Anwendungsfall
Ähnlich dem Eignungsmodell für die Solarkollektoren, das in der Gauß'schen Transformationsfunktion erläutert wurde, die südliche Ausrichtung wird jedoch als weit günstiger angesehen.
Auswirkungen der Parameter
Mittelpunkt
Mittelpunkt: Entspricht dem Mittelpunkt der Gauß'schen Funktion, bezeichnet die Mitte der Funktionskurve.
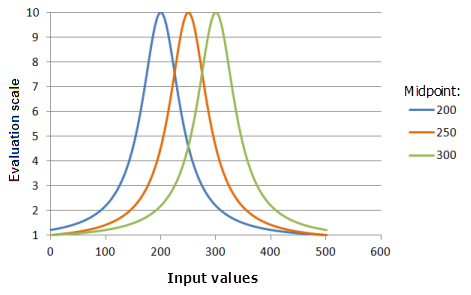
Verwendete Funktion im Schaubild oben:
- TfNear(Midpoint, 0.000576, 0, 1, 500, 10)
Für Midpoint werden folgende Werte verwendet: 200, 250 und 300. Der Mittelpunkt 250 und die Spanne von 0,000576 sind die standardmäßig berechneten Parameterwerte für das Eingabe-Dataset, das sich im Bereich 0 bis 500 befindet.
Spanne
Der Parameter Spanne unterscheidet sich nur dadurch von der Gauß'schen Funktion, dass sich die Eingabewerte mit zunehmendem Abstand vom Mittelpunkt stärker ändern.
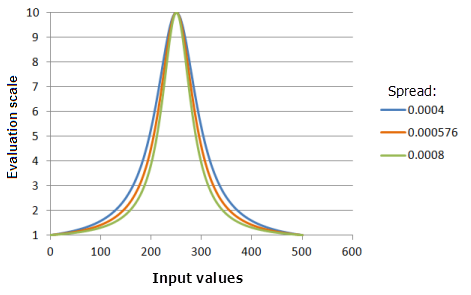
Verwendete Funktion im Schaubild oben:
- TfNear(250, Spread, 0, 1, 500, 10)
Für Spread werden folgende Werte verwendet: 0,0004, 0,000576 und 0,008. Der Mittelpunkt 250 und die Spanne von 0,000576 sind die standardmäßig berechneten Parameterwerte für das Eingabe-Dataset, das sich im Bereich 0 bis 500 befindet.
Power
Übersicht
Bei der Transformationsfunktion Potenz wird mithilfe eines angegebenen Versatzes eine Potenzfunktion mit einem angegebenen Exponenten auf die Eingabedaten angewendet. In einem Eignungsmodell ist eine Potenzfunktion besonders geeignet, wenn die niedrigsten Eingabewerte am ungünstigsten sind, die Präferenz mit steigenden Eingabewerten jedoch zunimmt, bis sie bei den größeren Eingabewerten schneller steigt (dieses Verhalten ist abhängig vom Exponenten).
Anwendungsfall
In einem Eignungsmodell zum Ermitteln des Standorts eines Atomkraftwerks, um für das Sicherheitskriterium die Entfernung von Störungszonen neu zu skalieren. Die Präferenz von weiter von einer Störungszone entfernt liegenden Standorten nimmt abhängig von der Potenzfunktion stetig zu, d. h., Standorte, die weiter von der Störungszone entfernt liegen, werden als wesentlich günstiger angesehen als Standorte, die näher an der Störungszone liegen.
Auswirkungen der Parameter
Verschieben
Der Parameter Versatz wird von den Eingabewerten subtrahiert und kann den ersten Eingabewert für die Potenzberechnungen bestimmen. Im Anwendungsfall mit dem Atomkraftwerk wurde beispielsweise festgelegt, dass das Kraftwerk an einem Standort gebaut werden muss, der sich mindestens 10 km von der Störungszone entfernt befindet. Es empfiehlt sich, die Funktion zu versetzen, sodass die Potenzfunktion bei 10 Kilometern beginnt.
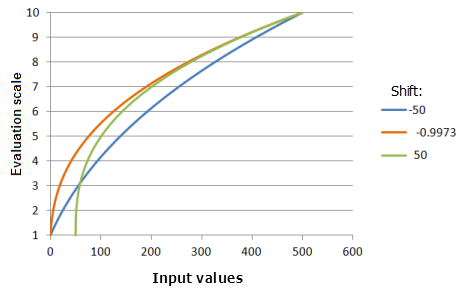
Verwendete Funktion im Schaubild oben:
- TfPower(Shift, 0.3704, 0, 1, 500, 10)
Für Shift werden folgende Werte verwendet: -50,0, -0,9973 und 50,0. Der Versatz um -0,9973 und der Exponent 0,3704 sind die standardmäßig berechneten Parameterwerte für das Eingabe-Dataset, das sich im Bereich 0 bis 500 befindet.
Exponent
Der Parameter Exponent bestimmt, wie steil die Potenzfunktion steigt. Je größer der Exponent, desto steiler ist die Funktionskurve, insbesondere bei höheren Eingabewerten.
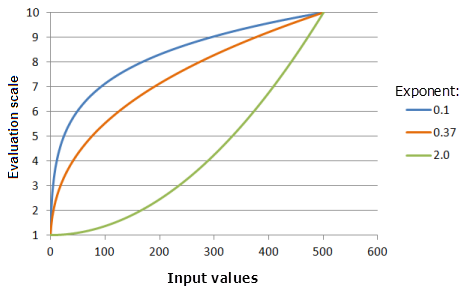
Eingabeparameter für das Diagramm oben:
- TfPower(-0.9973, Exponent, 0, 1, 500, 10)
Für Exponent werden folgende Werte verwendet: 0,1, 0,37 und 2,0. Der Versatz um -0,9973 und der Exponent 0,3704 sind die standardmäßig berechneten Parameterwerte für das Eingabe-Dataset, das sich im Bereich 0 bis 500 befindet.
Funktion "Klein"
Übersicht
Die Transformationsfunktion Klein wird verwendet, wenn die niedrigeren Eingabewerte als günstiger angesehen werden. Der definierte Mittelpunkt bezeichnet den Übergangspunkt der Funktion. Eingabewerte, die höher als der Mittelpunkt sind, stellen eine zunehmende Präferenz dar, darunter liegende Werte dagegen eine abnehmende Präferenz. Wie schnell die Werte mit zunehmendem Abstand vom Mittelpunkt zu- und abnehmen, wird durch den formbestimmenden Parameter Spanne festgelegt.
Anwendungsfall
In einem Baueignungsmodell kann es empfehlenswert sein, die Entfernung zum Straßen-Dataset aufgrund des Kriteriums der Baukosten neu zu skalieren. Die Standorte, die näher an den Straßen liegen (niedrige Werte), verfügen über die höchste Präferenz (niedrige Kosten). Die Präferenzwerte nehmen mit zunehmender Entfernung von der Straße stetig ab.
Auswirkungen der Parameter
Mittelpunkt
Mittelpunkt: Bezeichnet den Übergangspunkt der Funktion. Wenn der Mittelpunkt auf einen Wert über dem Mittelpunktwert der Eingabedaten verschoben wird, ändert sich der Übergangspunkt. Dies führt zu einer Zunahme der Präferenz im Bereich der niedrigeren Werte links vom Mittelpunkt, wobei die Präferenz langsamer steigt.
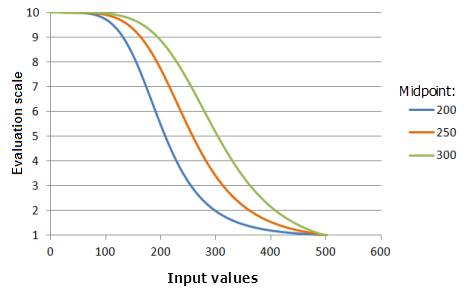
Verwendete Funktion im Schaubild oben:
- TfSmall(Midpoint, 5, 0, 1, 500, 10)
Für Midpoint werden folgende Werte verwendet: 200, 250 und 300. Der Mittelpunkt 250 und die Spanne von 5 sind die standardmäßigen Parameterwerte für das Eingabe-Dataset, das sich im Bereich 0 bis 500 befindet.
Spanne
Spanne: Legt fest, wie schnell die Präferenz zu- und abnimmt. Mit zunehmendem Spannenwert nimmt die Präferenz der Eingabewerte, die kleiner als der Mittelpunkt sind, gegen den unteren Grenzwert schneller zu, und die Eingabewerte, die höher als der Mittelpunkt sind, nehmen gegen den oberen Grenzwert schneller ab.
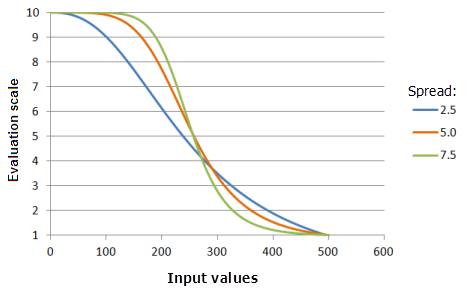
Verwendete Funktion im Schaubild oben:
- TfSmall(250, Spread, 0, 1, 500, 10)
Für Spread werden folgende Werte verwendet: 2,5, 5,0 und 7,5. Der Mittelpunkt 250 und die Spanne von 5 sind die standardmäßigen Parameterwerte für das Eingabe-Dataset, das sich im Bereich 0 bis 500 befindet.
Funktion "Symmetrisch Linear"
Übersicht
Bei der Transformationsfunktion Symmetrisch Linear wird eine lineare Funktion, die um den Mittelpunkt von Minimum und Maximum gespiegelt wird, auf den Bereich zwischen den angegebenen Minimal- und Maximalwerten angewendet. Der dem gespiegelten Punkt entsprechende Eingabewert erhält den höchsten Präferenzwert. Die Eingabewerte nehmen bezüglich der Präferenz mit zunehmender Entfernung vom gespiegelten Punkt linear ab. Alle Eingabewerte unter dem Minimum, jedoch über Unterer Grenzwert oder über dem Maximum, jedoch unter Oberer Grenzwert werden dem Von-Maßstab zugewiesen.
Wenn Minimum größer als Maximum ist, wird eine negative lineare Beziehung (eine negative Neigung) erstellt.
Die Funktion "Symmetrisch Linear" ist am nützlichsten, wenn sich die höchste Präferenz beim Mittelpunktwert befindet und die Präferenzen linear zu- und abnehmen, je weiter sich die Eingabewerte vom Mittelpunkt entfernen.
Anwendungsfall
Ein krankheitsübertragendes Insekt ist bei 70 Grad Fahrenheit am wenigsten aktiv. Mit steigender oder sinkender Durchschnittstemperatur in Richtung der durchschnittlichen minimalen und maximalen Durchschnittstemperaturen im Untersuchungsgebiet ist das Insekt aktiver, sodass es zu mehr Krankheitsübertragungen auf Menschen kommt. Bei der Ermittlung des Standortes für eine regionale Freizeiteinrichtung gelten Gebiete mit einer Durchschnittstemperatur von 70 Grad Fahrenheit (21 Grad Celsius) als besonders günstig, wobei die Präferenz linear abnimmt, je weiter die Temperaturen unter den entsprechenden Wert sinken oder darüber steigen, bis die minimalen und maximalen Durchschnittstemperaturen im Untersuchungsgebiet erreicht werden.
Auswirkungen der Parameter
Minimum
Der Parameter Minimum bestimmt einen der Punkte, durch den die Funktion "SymmetricLinear" führen muss. Eine Änderung des Minimums kann auch zu einer Änderung des Mittelpunktes führen, an dem die Funktion gespiegelt wird. Es ist außerdem möglich, als Minimum anstelle des Minimums des Eingabe-Rasters einen Wert festzulegen, der der Präferenz des Phänomens für das Kriterium entspricht.
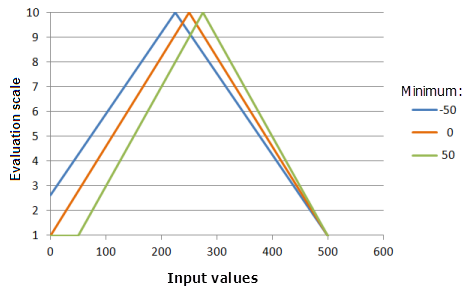
Verwendete Funktion im Schaubild oben:
- TfSymmetricLinear(Minimum, 500, 0, 1, 500, 10)
Für Minimum werden folgende Werte verwendet: -50, 0 und 50. Das Minimum 0 und das Maximum 500 sind die Standardparameterwerte für das Eingabe-Dataset, das sich im Bereich 0 bis 500 befindet.
Maximum
Maximum: Bestimmt den zweiten Punkt, durch den die Funktion "SymmetricLinear" führen muss. Eine Änderung des Maximums kann auch zu einer Änderung des Mittelpunktes führen, an dem die Funktion gespiegelt wird. Es ist außerdem möglich, als Maximum anstelle des Maximums des Eingabe-Rasters einen Wert festzulegen, der der Präferenz des Phänomens für das Kriterium entspricht.
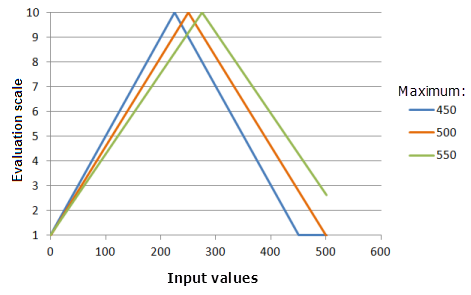
Verwendete Funktion im Schaubild oben:
- TfSymmetricLinear(0, Maximum, 0, 1, 500, 10)
Für Maximum werden folgende Werte verwendet: 450, 500 und 550. Das Minimum 0 und das Maximum 500 sind die Standardparameterwerte für das Eingabe-Dataset, das sich im Bereich 0 bis 500 befindet.