Funktionsweise von "Block-Statistiken"

Das Werkzeug Block-Statistiken führt einen Vorgang durch, bei der eine Statistik für Eingabezellen innerhalb einer festgelegten Anzahl von nicht überlappenden Fenstern oder Nachbarschaften berechnet wird. Die Statistik (z. B. "Mittelwert", "Maximum" oder "Summe") wird für alle innerhalb der entsprechenden Nachbarschaft enthaltenen Eingabezellen berechnet. Allen im kleinsten umgebenden Rechteck der angegebenen Nachbarschaft enthaltenen Zellenpositionen wird der resultierende Wert für die jeweilige Nachbarschaft oder den Block zugewiesen.

Nachbarschaftsverarbeitung

Konzeptuell gesehen berechnet der Algorithmus eine Statistik für die Eingabezellen in der angegebenen Nachbarschaftsform im jeweiligen Zellenblock. Da sich die Nachbarschaften nicht überlappen, wird jede Eingabezelle nur in die Berechnungen für einen Block einbezogen.

Es stehen mehrere vordefinierte Nachbarschaftsformen zur Auswahl. Sie können auch eine benutzerdefinierte Form erstellen. Die möglichen Statistiken, die Sie innerhalb einer Nachbarschaft berechnen können, sind Mehrheit, Maximum, Mittelwert, Medianwert, Minimum, Minderheit, Bereich, Standardabweichung, Summe und Varianz.

Im Grunde funktioniert das Werkzeug Block-Statistiken wie folgt:

• Es erstellt die erste angegebene Nachbarschaft - z. B. eine kreisförmige Nachbarschaft - in der oberen linken Ecke des Analysefensters.

  

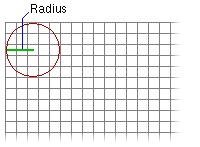
• Es berechnet das kleinste umgebende Rechteck, um die Größe des Ausgabeblocks zu bestimmen.

  

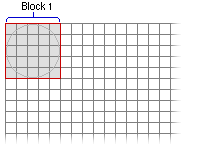
• Es partitioniert die verbleibende Fläche des Rasters in definierte Blöcke. Die Blöcke dürfen einander nicht überlappen.

  

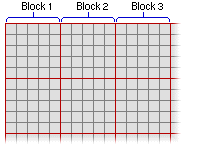
• Es identifiziert in jedem Block die Zellenpositionen, die in den Blockberechnungen verwendet werden. Die Zellenpositionen werden von der Definition der angegebenen Nachbarschaft – z. B. einer kreisförmigen Nachbarschaft – bestimmt, die in das umgebende Rechteck passt.

  

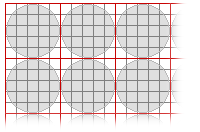
• Es berechnet den Ausgabewert für jede Nachbarschaft jedes Blocks. Jeder Zellenposition im entsprechenden Ausgabeblock werden die resultierenden Werte zugewiesen.

NoData-Zellen

Mit dem Parameter NoData-Werte in Berechnungen ignorieren wird gesteuert, wie NoData-Zellen im Nachbarschaftsfenster verarbeitet werden. Wenn dieser Parameter aktiviert ist (ignore_nodata = "DATA" in Python), werden bei der Berechnung des Ausgabewertes für den Block alle NoData-Zellen in der Nachbarschaft ignoriert. Wenn er deaktiviert ist (ignore_nodata = "NODATA" in Python) und in der Nachbarschaft NoData-Zellen vorhanden sind, sind alle Zellen im Ausgabeblock NoData-Zellen.

Nachbarschaftsgröße

Die maximale Größe jeder Dimension einer Nachbarschaft ist auf 2.048 Zellen begrenzt. Demzufolge können rechteckige Nachbarschaften diese Anzahl an Zellen weder in horizontaler noch in vertikaler Richtung überschreiten. Für kreisförmige Nachbarschaften darf der Radius 1.023 Zellen nicht überschreiten.

Nachbarschaftstypen

Die Form einer Nachbarschaft kann ein Kreisring, Kreis, Rechteck oder Keil sein. Mit einer Kernel-Datei können Sie auch eine benutzerdefinierte Nachbarschaftsform definieren sowie bestimmten Zellen in der Nachbarschaft andere Gewichtungen zuweisen, bevor die Statistik berechnet wird.

Im Folgenden finden Sie Beschreibungen der Nachbarschaftsformen und Informationen über ihre Definition:

• Kreisring
  • Die Kreisringform besteht aus zwei ineinander eingebetteten Kreisen, die eine Kreisringform bilden. Zellen mit Zellenmittelpunkten, die außerhalb des Radius des kleineren Kreises, aber innerhalb des Radius des größeren Kreises liegen, werden in die Verarbeitung der Nachbarschaft einbezogen. Die Fläche zwischen den beiden Kreisen stellt die Kreisringnachbarschaft dar.
  • Der Radius wird in Zellen- oder Karteneinheiten identifiziert, die rechtwinklig zur X- bzw. Y-Achse gemessen werden. Wenn die Radien in Karteneinheiten angegeben werden, werden sie zu Radien in Zelleneinheiten konvertiert. Die resultierenden Radien in Zelleneinheiten erzeugen eine Fläche, die der anhand der ursprünglichen Radien in Karteneinheiten berechneten Fläche am ehesten entspricht. Jeder vom Kreisring umfasste Zellenmittelpunkt wird in die Verarbeitung der Nachbarschaft einbezogen.
  • Die Standardkreisringnachbarschaft ist ein innerer Radius einer Zelle und ein äußerer Radius von drei Zellen.
  • Die folgende Abbildung zeigt ein Beispiel für eine Kreisringnachbarschaft:

  

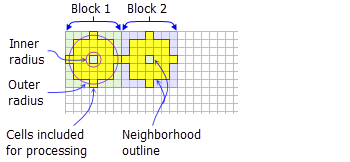
  Zwei Verarbeitungsblöcke mit Standard-Kreisringnachbarschaft (innerer Radius = 1 Zelle, äußerer Radius = 3 Zellen)

• Kreis
  • Eine Kreisnachbarschaft wird durch Angabe eines Radiuswertes erstellt.
  • Der Radius wird in Zellen- oder Karteneinheiten identifiziert, die rechtwinklig zur X- bzw. Y-Achse gemessen werden. Bei Angabe des Radius in Karteneinheiten wird zusätzliche Logik verwendet, um zu bestimmen, welche Zellen in die verarbeitete Nachbarschaft einbezogen werden. Zunächst wird die genaue Fläche eines durch den angegebenen Radiuswert definierten Kreises berechnet. Als nächstes wird die Fläche für zwei zusätzliche Kreise berechnet. Dabei wird der angegebene Radius des einen Kreises ab- und der des anderen aufgerundet. Diese beiden Flächen werden mit dem Ergebnis aus dem angegebenen Radius verglichen, wobei der Radius der Fläche, die sich am nächsten befindet, im Vorgang verwendet wird.
  • Der Standardradius für Kreisnachbarschaften entspricht drei Zellen.
  • Die folgende Abbildung zeigt ein Beispiel für eine Kreisnachbarschaft:

  

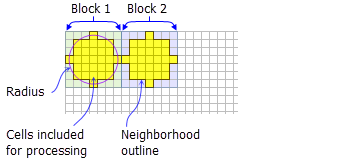
  Zwei Verarbeitungsblöcke mit Standard-Kreisnachbarschaft (Radius = 3 Zellen)

• Rechteck
  • Die Rechtecknachbarschaft wird durch Angabe einer Breite und einer Höhe in Zellen- oder Karteneinheiten festgelegt.
  • Es werden nur die Zellen als Teil der Rechtecknachbarschaft verarbeitet, deren Mittelpunkte im definierten Objekt liegen.
  • Die Standardrechtecknachbarschaft ist ein Quadrat mit einer Breite und Höhe von drei Zellen.
  • Die folgende Abbildung zeigt ein Beispiel für eine Rechtecknachbarschaft:

  

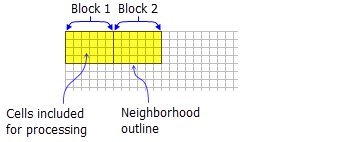
  Darstellung von zwei Verarbeitungsblöcken mit einer Rechtecknachbarschaft (Breite= 6 Zellen, Höhe = 4 Zellen)

• Keil
  • Ein Keil ist eine keilförmige Nachbarschaft, die durch einen Radius, einen Anfangs- und einen Endwinkel angegeben wird.
  • Der Keil dehnt sich gegen den Uhrzeigersinn vom Anfangswinkel zum Endwinkel aus. Winkel werden in arithmetischen Grad von 0 bis 360 angegeben, wobei 0 eine positive X-Achse (3:00 auf einer Uhr) ist und ein Ganzzahl- oder ein Gleitkommawert sein kann. Es können negative Winkel verwendet werden.
  • Der Radius wird in Zellen- oder Karteneinheiten identifiziert, die rechtwinklig zur X- bzw. Y-Achse gemessen werden. Wenn der Radius in Karteneinheiten angegeben wird, wird er zu einem Radius in Zelleneinheiten konvertiert. Der resultierende Radius in Zelleneinheiten erzeugt eine Fläche, die der anhand des ursprünglichen Radius in Karteneinheiten berechneten Fläche am ehesten entspricht. Jeder vom Keil umfasste Zellenmittelpunkt wird in die Verarbeitung der Nachbarschaft einbezogen.
  • Die Standardkeilnachbarschaft reicht von 0 bis 90 Grad mit einem Radius von drei Zellen.
  • Die folgende Abbildung zeigt ein Beispiel für eine Keilnachbarschaft:

  

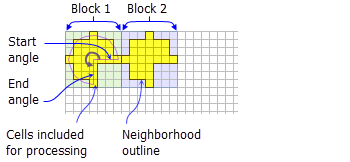
  Darstellung von zwei Verarbeitungsblöcken mit Keilnachbarschaft (Radius = 3 Zellen, Anfangswinkel = 0, Endwinkel = 270)

• Unregelmäßig
  • Ermöglicht die Angabe einer unregelmäßig gestalteten Nachbarschaft.
  • Die unregelmäßige Kernel-Datei gibt an, welche Zellenpositionen in der Nachbarschaft enthalten sein sollten.
  • Folgendes gilt für eine Kernel-Datei bei einer unregelmäßigen Nachbarschaft:
    • Die unregelmäßige Kernel-Datei ist eine ASCII-Textdatei, die die Werte und die Form einer unregelmäßigen Nachbarschaft definiert. Die Datei kann mit einem beliebigen Texteditor erstellt werden. Sie muss die Erweiterung .txt aufweisen.
    • Die erste Zeile gibt die Breite und die Höhe der Nachbarschaft an (die Anzahl der Zellen in der X-Richtung, gefolgt von einem Leerzeichen und der Anzahl der Zellen in der Y-Richtung).
    • In den nachfolgenden Zeilen wird der Wert definiert, der an den einzelnen Positionen in der dadurch dargestellten Nachbarschaft verwendet werden soll. Ein Leerzeichen zwischen jedem Wert ist notwendig.
    • Mit den Werten wird festgelegt, ob eine Position in der Nachbarschaft in die Berechnung einbezogen wird. In der Regel wird der Wert 1 verwendet, um die Positionen anzugeben, die in die Berechnungen einer unregelmäßigen Nachbarschaft einbezogen werden sollen. Es kann jedoch ein beliebiger positiver oder negativer Wert ungleich null verwendet werden. Auch Gleitkommawerte können verwendet werden.
    • Wenn Sie eine Position in der Nachbarschaft von der Berechnung ausschließen möchten, verwenden Sie an der entsprechenden Position in der Kernel-Datei den Wert 0 (kein Leerzeichen).

  • Ein Beispiel für eine unregelmäßige ASCII-Kernel-Datei und die dadurch dargestellte Nachbarschaft folgen:

  

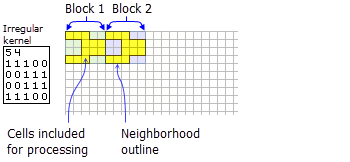
  Darstellung eines unregelmäßigen Nachbarschafts-Kernels mit den Zellen, die zur Verarbeitung für zwei Blöcke einbezogen werden

• Gewichtung
  • Ähnlich wie beim unregelmäßigen Nachbarschaftstyp können Sie anhand der Gewichtungs-Nachbarschaft eine unregelmäßige Nachbarschaft definieren und außerdem Gewichtungen auf die Eingabewerte anwenden.
  • In der Gewichtungs-Kernel-Datei werden die Zellenpositionen, die in der Nachbarschaft einbezogen werden sollen, und die Gewichtungen angegeben, mit denen sie multipliziert werden.
  • Die Gewichtungs-Nachbarschaft ist nur für die Statistiktypen "Mittelwert", "Standardabweichung" und "Summe" verfügbar.
  • Folgendes gilt für die Kernel-Datei bei einer Gewichtungs-Nachbarschaft:
    • Die Gewichtungs-Kernel-Datei ist eine ASCII-Textdatei, die die Werte und die Form einer Gewichtungs-Nachbarschaft definiert. Die Datei kann mit einem beliebigen Texteditor erstellt werden. Sie muss die Erweiterung .txt aufweisen.
    • Die erste Zeile gibt die Breite und die Höhe der Nachbarschaft an (die Anzahl der Zellen in der X-Richtung, gefolgt von einem Leerzeichen und der Anzahl der Zellen in der Y-Richtung).
    • In den nachfolgenden Zeilen wird der Wert definiert, der an den einzelnen Positionen in der dadurch dargestellten Nachbarschaft verwendet werden soll. Ein Leerzeichen zwischen jedem Wert ist notwendig.
    • Bei der Statistik "Summe" kann eine Gewichtung ein positiver Wert, ein negativer Wert, eine ganze Zahl oder ein Gleitkommawert sein.
    • Bei der Statistik "Mittelwert" und "Standardabweichung" kann eine Gewichtung eine positive ganze Zahl oder ein Gleitkommawert sein. Negative Werte sind bei diesen Statistiken nicht zulässig, sodass Positionen mit einer negativen Gewichtung bei den Berechnungen ignoriert werden.
    • Wenn Sie eine Position in der Nachbarschaft von der Berechnung ausschließen möchten, verwenden Sie an der entsprechenden Position in der Kernel-Datei den Wert 0 (kein Leerzeichen).

  • Beispiel für den Inhalt einer gewichteten Kernel-Datei und die dadurch dargestellte Nachbarschaft:

  

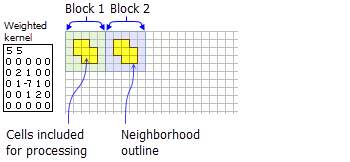
  Darstellung eines gewichteten Nachbarschafts-Kernels mit den Zellen, die zur Verarbeitung für zwei Blöcke einbezogen werden

Statistiktyp

Die verfügbaren Statistiken sind: "Mehrheit", "Maximum", "Mittelwert", "Medianwert", "Minimum", "Minderheit", "Bereich", "Standardabweichung", "Summe" und "Varianz". Der Standardstatistiktyp ist "Mittelwert".

• Mehrheit
  • Als Eingabe kann nur ein Ganzzahl-Raster verwendet werden.
  • Damit wird die Häufigkeit der einzelnen Zelleneinzelwerte in der jeweiligen Blocknachbarschaft bestimmt. Wenn ein einzelner Wert die höchste Häufigkeit aufweist (am häufigsten vorkommt), wird dieser Wert allen Zellen in dieser Nachbarschaft zugewiesen. Bei einem Gleichstand wird der niedrigste Wert zugewiesen.
• Maximum
  • Wenn das Eingabe-Raster ein Ganzzahl-Raster ist, sind die Werte des Ausgabe-Rasters Ganzzahlwerte; wenn die Werte der Eingabe Gleitkommawerte sind, sind die Werte der Ausgabe Gleitkommawerte.
• Mittelwert
  • Die Eingabe kann ein ganzzahliges oder Gleitkomma-Raster sein.
  • Das Ausgabe-Raster ist immer ein Gleitkomma-Raster.
  • Beim Gewichtungs-Nachbarschaftstyp ist dies einer der unterstützten Statistiktypen. Informationen zum Berechnen dieser Statistik finden Sie im Abschnitt Gewichtete Nachbarschaft.
• Medianwert
  • Als Eingabe kann nur ein Ganzzahl-Raster verwendet werden.
  • Wenn die Anzahl der gültigen Zellenwerte in der Nachbarschaft ungerade ist, wird der Medianwert durch das Ordnen der Werte und Auswählen des mittleren Wertes berechnet. Bei einer geraden Anzahl von Werten in einer Nachbarschaft werden die Werte geordnet, und es wird der niedrigere der beiden mittleren Werte ausgewählt.
• Minimum
  • Wenn das Eingabe-Raster ein Ganzzahl-Raster ist, sind die Werte des Ausgabe-Rasters Ganzzahlwerte; wenn die Werte der Eingabe Gleitkommawerte sind, sind die Werte der Ausgabe Gleitkommawerte.
• Minderheit
  • Als Eingabe kann nur ein Ganzzahl-Raster verwendet werden.
  • Damit wird die Häufigkeit der einzelnen Zelleneinzelwerte in der jeweiligen Blocknachbarschaft bestimmt. Wenn ein einzelner Wert die geringste Häufigkeit aufweist (am seltensten vorkommt), wird dieser Wert allen Zellen in dieser Nachbarschaft zugewiesen. Bei einem Gleichstand wird der niedrigste Wert zugewiesen.
• Bereich
  • Wenn das Eingabe-Raster ein Ganzzahl-Raster ist, sind die Werte des Ausgabe-Rasters Ganzzahlwerte; wenn die Werte der Eingabe Gleitkommawerte sind, sind die Werte der Ausgabe Gleitkommawerte.
  • Die Werte für jede Zellenposition im Ausgabe-Raster werden auf Zellenbasis bestimmt, indem diese einfache Formel angewendet wird: Block Range = Block Maximum – Block Minimum.
• Standardabweichung
  • Das Ausgabe-Raster ist immer ein Gleitkomma-Raster.
  • Beim Gewichtungs-Nachbarschaftstyp ist dies einer der unterstützten Statistiktypen. Informationen zum Berechnen dieser Statistik finden Sie im Abschnitt Gewichtete Nachbarschaft.
  • Die Standardabweichung wird in Bezug auf die gesamte Bevölkerung berechnet (die N-Methode) und nicht auf Grundlage einer Auswahl geschätzt (die N-1-Methode).
• Summe
  • Wenn das Eingabe-Raster ein Ganzzahl-Raster ist, sind die Werte des Ausgabe-Rasters Ganzzahlwerte; wenn die Werte der Eingabe Gleitkommawerte sind, sind die Werte der Ausgabe Gleitkommawerte.
  • Beim Gewichtungs-Nachbarschaftstyp ist dies einer der unterstützten Statistiktypen. Informationen zum Berechnen dieser Statistik finden Sie im Abschnitt Gewichtete Nachbarschaft.
• Varianz
  • Als Eingabe kann nur ein Ganzzahl-Raster verwendet werden.

Berechnungen gewichteter Nachbarschaften

Der Einfluss, den die einzelnen Werte in der Nachbarschaft auf das Endergebnis des Verarbeitungsblocks haben, kann durch Anwenden von Gewichtungen angepasst werden.

In den folgenden Abschnitten werden die Formeln für die Berechnung der Ergebnisse für den gewichteten Mittelwert, die Standardabweichung und die Summenstatistik vorgestellt. Dabei wird jeweils ein Beispiel für die Berechnung für einen Verarbeitungsblock und die Ergebnisse für eine rechteckige 3x3-Zellennachbarschaft angegeben.

Statistik für gewichteten Mittelwert

Bei der Gewichtungs-Nachbarschaft mit der Statistik "Mittelwert" entspricht der Ausgabewert für die Zellen in einem Verarbeitungsblock der Summe des Produkts der Kernel-Gewichtungswerte multipliziert mit den Eingabewerten, dividiert durch die Summe der Kernel-Gewichtungswerte.

Die Formel, die auf die Zellen innerhalb einer Nachbarschaft angewendet wird, lautet wie folgt:

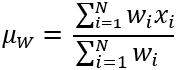
Wobei gilt:

• µ_W ist der nach Bevölkerung gewichtete Mittelwert für den Verarbeitungsblock.
• N ist die Anzahl der Zellen in der Nachbarschaft.
• w_i ist der im Kernel definierte Gewichtungswert.
• x_i ist ein Eingabezellenwert.

Vorversion:

In früheren Versionen wurde für die Berechnungen die Anzahl der Zellen in der Nachbarschaft als Nenner verwendet.

Gewichtungswerte müssen positive ganze Zahlen oder positive Gleitkommazahlen sein.

Beispiel

Betrachten wir den folgenden 3x3-Rechteckblock aus Eingabezellen:

4 6 7 6 7 8 4 5 6

Das arithmetische Mittel (Summe/Anzahl) dieser Werte beträgt 53/9 = 5,889.

Betrachten wir den folgenden gewichteten 3x3-Zell-Kernel:

3 3 0,0 0,5 0,0 0,5 2,0 0,5 0,0 0,5 0,0

Dieser Kernel verleiht der mittleren Zelle des Blocks den größten Einfluss (Gewichtung 2), verringert den Einfluss der vier orthogonalen Nachbarn der mittleren Zelle (Gewichtung 0,5) und sorgt dafür, dass die vier Eckzellen keinen Einfluss haben (Gewichtung 0).

Im Folgenden werden die Berechnungen zur Ermittlung des endgültigen Wertes mithilfe der oben angegebenen Gleichung für den gewichteten Mittelwert angegeben:

= (w1x1 + w2x2 + w3x3 + w4x4 + w5x5 + w6x6 + w7x7 + w8x8 + w9x9) / (w1 + w2 + w3 + w4 + w5 + w6 + w7 + w8 + w9) = ((0*4)+(0,5*6)+(0*7)+(0,5*6)+(2,0*7)+(0,5*8)+(0*4)+(0,5*5)+(0*6)) / (0+0,5 + 0 + 0,5 + 2,0 + 0,5 + 0 + 0,5 + 0) = (0 + 3,0 + 0 + 3,0 + 14,0 + 4,0 + 0 + 2,5 + 0) / (0,5 + 0,5 + 2,0 + 0,5 + 0,5) = (3,0 + 3,0 + 14,0 + 4,0 + 2,5) / 4,0 = 26,5 / 4,0 = 6,625

Zum Vergleich: Der reguläre Durchschnitt der neun Eingabezellen würde 5,889 betragen. Werden nur die fünf Eingabezellen berücksichtigt, die sich innerhalb des Kernels befinden (wobei die Gewichtung != 0 beträgt), ohne dass die Werte der Gewichtungen berücksichtigt werden, ergibt sich ein Durchschnittswert von 6,4 (6 + 6 + 7 + 8 + 5 = 32, der durch die Anzahl von fünf geteilt wird).

Statistik für gewichtete Standardabweichung

Bei der Gewichtungs-Nachbarschaft mit der Statistik "Standardabweichung" entspricht der Ausgabewert für die Zellen in einem Verarbeitungsblock dem Ergebnis der folgenden Gleichung:

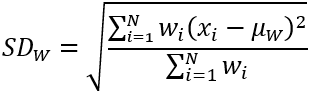
Wobei gilt:

• SD_W ist der nach Bevölkerung gewichtete Wert der Standardabweichung für den Verarbeitungsblock.
• µ_W ist der nach Bevölkerung gewichtete Mittelwert für den Verarbeitungsblock.
• N ist die Anzahl der Zellen in der Nachbarschaft.
• w_i ist der im Kernel definierte Gewichtungswert.
• x_i ist ein Eingabezellenwert.

Gewichtungswerte müssen positive ganze Zahlen oder positive Gleitkommazahlen sein.

Wenn alle Eingabewerte in einer Nachbarschaft identisch sind, lautet der Wert der Standardabweichung für alle Zellen in einem Verarbeitungsblock 0.

Beispiel

Für dieses Beispiel werden die Nachbarschaftswerte verwendet, die im obigen Beispiel für den gewichteten Mittelwert verwendet wurden.

4 6 7 6 7 8 4 5 6

Hier werden auch dieselben gewichteten Kernel-Werte verwendet:

3 3 0,0 0,5 0,0 0,5 2,0 0,5 0,0 0,5 0,0

Wird die oben angegebene gewichtete Standardabweichung für den Zellenblock angewendet, ergibt sich ein Wert von etwa 0,85696. Dieser Wert wird in jede Zelle in dieser Blocknachbarschaft geschrieben.

Statistik für gewichtete Summe

Bei der Gewichtungs-Nachbarschaft mit der Statistik "Summe" entspricht der Ausgabewert für die Zellen in einem Verarbeitungsblock dem Ergebnis der folgenden Gleichung:

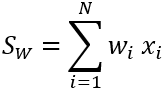
Wobei gilt:

• S_W ist der gewichtete Summenwert für den Verarbeitungsblock.
• N ist die Anzahl der Zellen in der Nachbarschaft.
• w_i ist der im Kernel definierte Gewichtungswert.
• x_i ist ein Eingabezellenwert.

Gewichtungswerte können positive oder negative ganze Zahlen oder Gleitkommazahlen sein.

Beispiel

Betrachten wir die folgenden Eingabewerte für die Nachbarschaft:

4 6 7 6 7 8 4 5 6

Betrachten wir den folgenden gewichteten 3x3-Zell-Kernel:

3 3 –1 –2 –1 0 0 0 1 2 1

Im Folgenden werden die Berechnungen zur Ermittlung des endgültigen Wertes mithilfe der obigen Gleichung angegeben:

= (w1x1 + w2x2 + w3x3 + w4x4 + w5x5 + w6x6 + w7x7 + w8x8 + w9x9) = ((-1*4) + (-2*6) + (-1*7) + (0*6) + (0*7) + (0*8) + (1*4) + (2*5) + (1*6)) = (-4) + (-12) + (-7) + 4 + 10 + 6 = -3