Fuzzy-Logik kann als Überlagerungsanalysetechnik verwendet werden, um traditionelle Anwendungen der Überlagerungsanalyse, z. B. Siteauswahl und Eignungsmodelle, zu lösen.
Die grundlegende Prämisse hinter der Fuzzy-Logik besteht darin, dass es Ungenauigkeiten in Attributdaten und in der Geometrie von räumlichen Daten gibt. Fuzzy-Logik stellt Techniken bereit, um Ungenauigkeiten beider Typen zu berücksichtigen. Da sie aber die Überlagerungsanalyse betrifft, konzentriert sich Fuzzy-Logik auf Ungenauigkeiten in Attributdaten. Die zwei wichtigsten Bereiche, in denen Ungenauigkeiten in Attributdaten entstehen, sind die Definition der Klassen und die Messung des Phänomens. Diese beiden Quellen von Ungenauigkeiten, insbesondere die Definition der Klassen, können Ungenauigkeiten beim Zuweisen von Zellen zu bestimmten Klassen verursachen.
Die Definition der Klassen in einer Klassifizierung und die Ungenauigkeit beim Zuweisen von Phänomenen zu Klassen können sich auf die Entscheidungsfindung auswirken. Die Werkzeuge für die Fuzzy-Überlagerung helfen den Entscheidungsträgern beim Treffen von Entscheidungen unter Berücksichtigung dieser Ungenauigkeiten. Fuzzy-Logik konzentriert sich auf die Modellierung der Ungenauigkeiten von Klassengrenzen.
Die Werkzeuge Gewichtete Überlagerung und Gewichtete Summe basieren auf exakten Mengen, bei denen jede Zelle entweder in einer Klasse ist oder nicht. Fuzzy-Logik konzentriert sich besonders auf Situationen, bei denen die Grenzen zwischen Klassen nicht klar sind. Im Gegensatz zu exakten Mengen geht es bei Fuzzy-Logik nicht darum, ob ein Element in einer Klasse ist oder nicht. Sie definiert, wie wahrscheinlich es ist, dass das Phänomen ein Element einer Menge (oder Klasse) ist. Fuzzy-Logik basiert auf der Mengenlehre. Deshalb definieren Sie nicht Wahrscheinlichkeiten, sondern Möglichkeiten.
Wenn zum Beispiel in einem Eignungsmodell zum Wohnen die Neigung eines der Eingabekriterien ist, wird jeder Neigungswert transformiert oder erhält einen Wert zwischen 0 und 1 für die Möglichkeit, dass dieser Neigungswert ein Element der Eignungsmenge für das Bauen (oder der Klasse) ist (also geeignet ist). Der Wert 1 gibt an, dass der Wert mit absoluter Sicherheit Teil der Menge ist, während der Wert 0 angibt, dass der Wert mit absoluter Sicherheit nicht Teil der Menge ist. Alle anderen Werte weisen einen bestimmten Grad der Möglichkeit auf, wobei die höheren Werte eine höhere Wahrscheinlichkeit der Zugehörigkeit angeben. Der Prozess zum Transformieren der ursprünglichen Eingabewerte entsprechend der Möglichkeit der Zugehörigkeit in eine Skala von 0 bis 1 wird als Fuzzyfizierung bezeichnet. Dabei wird jedes Kriterium für das Modell (z. B. Ausrichtung, Entfernung zu Straßen und Land-Use-Typ) fuzzyfiziert. Das Werkzeug Fuzzy-Zugehörigkeit wird verwendet, um die Daten in die Skala der Möglichkeiten von 0 bis 1 zu transformieren.
Um die Positionen zu bestimmen, die alle Kriterien am besten erfüllen (also eine hohe Wahrscheinlichkeit der Zugehörigkeit in allen Mengen aufweisen), wird das Werkzeug Fuzzy-Überlagerung verwendet. Bei einer Kombination mehrerer Kriterien analysiert das Werkzeug Fuzzy-Überlagerung die Wahrscheinlichkeit, dass die Zelle ein Element jeder Menge ist, die durch diese Mehrfachkriterien definiert wird. Wie hoch ist zum Beispiel die Wahrscheinlichkeit, dass eine bestimmte Position zu einer guten Eignung für Neigung, Ausrichtung und Entfernung zu Straßen gehört?
Deshalb sind die zwei Hauptschritte in der Fuzzy-Logik für die Überlagerungsanalyse die Fuzzyfizierung oder der Fuzzy-Zugehörigkeitsprozess und die Fuzzy-Überlagerungsanalyse. Diese zwei Schritte entsprechen den Schritten zum Reklassifizieren/Transformieren bzw. zum Hinzufügen/Kombinieren im allgemeinen Überlagerungsprozess.
Ob etwas zu einer Klasse gehört oder nicht, lässt sich oftmals nicht klar abgrenzen, ist jedoch subjektiv. In der menschlichen Sprache werden diese Ungenauigkeiten über Modifikatoren qualifiziert, wie zum Beispiel sehr, leicht und mäßig. Mit Fuzzy-Logik läuft die Überlagerungsanalyse mehr wie natürliches menschliches Denken ab. Die Dinge sind nicht klar umrissen, die Grenzen können unscharf sein. Fuzzy-Logik ist nicht die Analyse der Unsicherheit in den Daten, sondern erkundet die Ungenauigkeit von Klassengrenzen.
In den folgenden Abschnitten werden die Probleme mit der Datenklassifizierung, dem Fuzzy-Zugehörigkeitsprozess und der Durchführung der Fuzzy-Überlagerungsanalyse beschrieben. Beschrieben werden auch ein Vergleich der Fuzzy-Logik mit binären und gewichteten Überlagerungsanalysetechniken und die Möglichkeit der Integration der Fuzzy-Logik in den allgemeinen Überlagerungsprozess.
Datenklassifizierung und Fuzzy-Logik
Um Phänomene zu beschreiben oder zu ordnen, können Sie sie allgemein in Klassen charakterisieren. Beispiele für Klassen sind Land-Use-Kategorie, Bodenart, Eignungsgewichtung, Straßenklasse und Vegetationsart. In exakten Mengen ist die Zugehörigkeit binär, das heißt, das Phänomen ist entweder ein Element der Klasse oder kein Element der Klasse. Die Klassengrenzen sind scharf. Aufgrund von Ungenauigkeit im Denken, mehrdeutigen Kategorisierungsregeln, Vagheit und Ambivalenz sind die Grenzen zwischen Klassen nicht immer klar.
Wenn das Phänomen, das Sie erkunden, zum Beispiel die Beziehung der unterschiedlichen Größen der Menschen innerhalb einer Gruppe ist, dann können Sie beginnen, indem Sie die unterschiedlichen Menschen entsprechend ihrer Größe in Klassen zusammenfassen. Sie könnten mit drei Klassen beginnen: "Short", "Medium" und "Tall". Sie müssen die Grenzen für die Klassen festlegen. Zum Beispiel könnte als klein ("Short") eine Person mit einer Größe von 5 Fuß (1,524 Meter) oder darunter, als groß ("Tall") eine Person mit einer Größe von 6 Fuß (1,8288 Meter) und darüber, und als mittelgroß ("Medium") eine Person mit einer Größe zwischen 5 und 6 Fuß (1,6764 und 1,8288 Meter) gelten. Wenn eine Person eine Größe von 6 Fuß (1,8288 Meter) hat, wird sie in der Klasse "Tall" eingeordnet. Wenn eine Person eine Größe von 5 Fuß und 11 Zoll (1,8034 Meter) hat, wird sie als mittelgroß ("Medium") klassifiziert. Obwohl zwischen den Größen dieser zwei Personen eine Differenz von nur 1 Zoll (0,0254 Meter) besteht, werden sie in zwei separaten Klassen eingeordnet. Dieselbe Differenzbeziehung würde sich darstellen, wenn ein anderes Gruppenmitglied eine Größe von 5 Fuß und 1 Zoll (1,5494 Meter) und die zweite Person eine Größe von 6 Fuß und 6 Zoll (1,9812 Meter) hat. Wegen der Grobheit der Klassifizierungen können die vollständigen Beziehungen zwischen den Größen nicht erfasst werden.
Um die Größenbeziehungen zwischen den unterschiedlichen Menschen besser darzustellen, können weitere Klassen hinzugefügt werden. Zum Beispiel könnten zwei weitere Klassen hinzugefügt werden. Danach wären fünf Klassen vorhanden: "Short" für kleine Personen mit einer Größe von 4 Fuß und 10 Zoll (1,4732 Meter) oder darunter, "Medium Short" für mittelgroße Personen mit einer Größe von 4 Fuß und 10 Zoll (1,4732 Meter) bis 5 Fuß und 4 Zoll (1,6256 Meter), "Medium Height" für mittelgroße Personen mit einer Größe von 5 Fuß und 4 Zoll (1,6256 Meter) bis 5 Fuß und 10 Zoll (1,778 Meter), "Medium Tall" für mittelgroße Personen mit einer Größe von 5 Fuß und 10 Zoll (1,778 Meter) bis 6 Fuß und 4 Zoll (1,9304 Meter) und "Tall" für große Personen mit einer Größe von mehr als 6 Fuß und 4 Zoll (1,9304 Meter). Mit dieser Verfeinerung der Klassen kann die Beziehung zwischen der Größe der Menschen genauer dargestellt werden.
Zur weiteren Verfeinerung können noch mehr Klassen hinzugefügt werden. Ungeachtet dessen, wie viele Klassen hinzugefügt werden, gibt es noch eine Generalisierung der Größenbeziehungen zwischen den Menschen. Es gibt Phänomene, die nicht in streng definierte Klassen klassifiziert werden können. Manchmal ist es schwierig, die Realität in diskontinuierliche Klassen zu gruppieren.
Wie zu sehen ist, kann die Definition der Klassengrenzen subjektiv sein und sich mit der Definition des Phänomens ändern. Bei den oben definierten Größenklassen wird davon ausgegangen, dass die Menschen Erwachsene sind und höchstwahrscheinlich eine Mischung aus Männern und Frauen bilden. Wenn die Gruppe nur aus Frauen besteht, dann müssten die Klassendefinitionen wohl geändert werden. Wenn die Gruppe ganz oder teilweise aus Kindern besteht, dann müssten die Klassengrenzen noch weiter geändert werden.
Die Definition der Klassen und die Merkmale des Phänomens bestimmen, wie das zu modellierende Phänomen dargestellt werden muss. Messfehler sind ein weiterer Teil des Problems der Klassifizierungen. Wenn das Verfahren zur Messung der Größe von Personen eine Genauigkeit von plus oder minus 1 Zoll (0,0254 Meter) hat, kann die Ungenauigkeit die Klasse, der ein Phänomen zugewiesen wird, ändern.
Fuzzy-Logik modelliert diese Ungenauigkeit im Klassifizierungsprozess. In Fuzzy-Logik werden die Klassen als Mengen definiert. Es gibt ein Verständnis dafür, wie der ideale Wert für die Zugehörigkeit in der Menge aussieht, zum Beispiel der ideale Neigungswert in einem Eignungsmodell zum Wohnen. Mit zunehmender Entfernung der Werte vom idealen Wert sinkt der Grad der Klarheit auf einen bestimmten Punkt ab, an dem klar ist, dass der Wert kein Element der Menge ist (weil es zum Beispiel zum Bauen definitiv zu steil ist).
Wenn Sie im obigen Beispiel einer Anwendung für die Körpergröße bei Ihren drei Größenklassen "Short", "Medium" und "Tall" bleiben, können diese drei Klassen in Fuzzy-Logik einander überlappen.
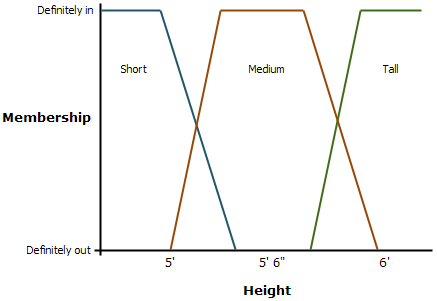
Im obigen Beispiel ist die Vollzugehörigkeit zu einer Klasse wie folgt definiert:
- Short: < 5 Fuß (1,524 Meter)
- Medium: 5 Fuß und 3,5 Zoll (1,6129 Meter) bis 5 Fuß und 8,5 Zoll (1,7399 Meter)
- Tall: > 6 Fuß (1,8288 Meter)
Für die "Short"-Menge ist eine Person mit einer Größe von 5 Fuß (1,524 Meter) oder darunter definitiv Teil der "Short"-Menge. In diesem Fall wird eine 1 zugewiesen. Jede Größe über 5 Fuß (1,524 Meter) und unter 5 Fuß und 3,5 Zoll (1,6129 Meter) ist zwischen der "Short"- und der "Medium"-Menge (oder -Klasse). Die Größen zwischen 5 Fuß (1,524 Meter) und 5 Fuß und 1,75 Zoll (1,6193 Meter) sind mit einer höheren Wahrscheinlichkeit Teil der "Short"-Menge. Die Größen von über 5 Fuß und 1,75 Zoll (1,6193 Meter) bis einschließlich 5 und 3,5 Zoll (1,6129 Meter) sind möglicherweise Teil der "Short"-Menge, aber mit einer höheren Wahrscheinlichkeit Teil der "Medium"-Menge.
Der Fuzzyfizierungsprozess wird im Allgemeinen über vordefinierte Funktionen mit dem Werkzeug Fuzzy-Zugehörigkeit implementiert.
Fuzzy-Zugehörigkeit
Der Fuzzyfizierungsprozess charakterisiert die Ungenauigkeit von Klassen für Phänomene, die keine klar definierten Grenzen aufweisen.
Bei der Fuzzyfizierung werden die ursprünglichen Werte des Phänomens in die Möglichkeit ihrer Zugehörigkeit zu einer definierten Menge konvertiert. Die definierte Menge kann aus Elementen bestehen, die geeignet sind oder in einer bestimmten Entfernung liegen oder die Möglichkeit haben, ein bestimmtes Mineral zu finden. In diesem Zugehörigkeitskontinuum werden die ursprünglichen Werte des Phänomens über vordefinierte Fuzzy-Zugehörigkeitsfunktionen oder über andere Reklassifizierungstechniken reklassifiziert.
Im Fuzzyfizierungsprozess wird die ideale Definition für die Zugehörigkeit zur Menge definiert. Jedem Wert des Phänomens, der zentraler zum Kern der Definition der Menge liegt, wird eine 1 zugewiesen. Allen Werten, die definitiv nicht Teil der Menge sind, wird eine 0 zugewiesen. Alle Werte, die zwischen diesen zwei Extremwerten liegen, befinden sich in der Übergangszone der Menge, der Grenze. Je weiter die Werte vom idealen Wert oder vom Mittelpunkt der Menge entfernt sind, desto kleiner ist der Wert auf einer kontinuierlich abnehmenden Skala von 1 bis 0, der ihnen zugewiesen wird. Je niedriger der zugewiesene Wert ist, desto geringer ist die Möglichkeit, dass der ursprüngliche Wert des Phänomens ein Element dieser Menge ist.
Der Fuzzyfizierungswert 0,5 ist der Übergangspunkt. Jeder Fuzzy-Wert größer als 0,5 bedeutet, dass der ursprüngliche Wert des Phänomens ein Element der Menge sein kann. Wenn die Fuzzyfizierungswerte unter 0,5 fallen, ist es weniger wahrscheinlich, dass der ursprüngliche Wert des Phänomens ein Element der Menge ist. Die Werte sind möglicherweise nicht Teil der Menge.
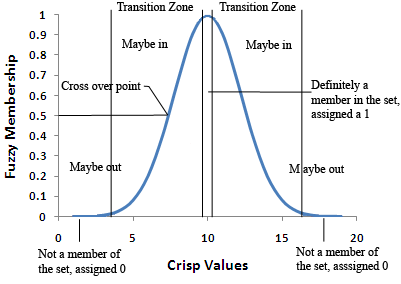
Die Breite der Übergangszone hängt von dem zu modellierenden Phänomen, davon, was über dieses Phänomen bekannt ist, von der Definition der Menge und von der Genauigkeit der Messung ab. Durch Änderung der Parameter der Fuzzyfizierungssfunktion können die Merkmale der Übergangszone definiert werden. In der folgenden Abbildung ist die Gauß'sche Fuzzy-Zugehörigkeitsfunktion mit drei verschiedenen Kurven, die anhand der geänderten Parameter der Funktion abgeleitet wurden, dargestellt.
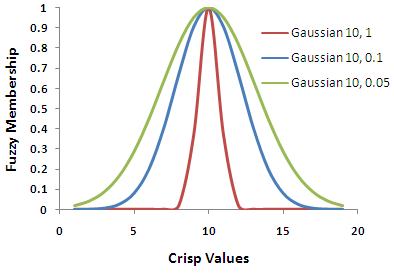
Die Parameter diesen als Modifikatoren für die Definition der Menge. Die Modifikatoren charakterisieren die mögliche Überlappung oder den Mittelweg zwischen Mengen.
Der Fuzzyfizierungsprozess wird für jedes Kriterium in der Überlagerungsanalyse durchgeführt.
Fuzzy-Überlagerungsverfahren
Um die Beziehungen und Wechselwirkungen zwischen allen Mengen für die Mehrfachkriterien im Überlagerungsmodell zu analysieren, werden Fuzzy-Überlagerungsverfahren verwendet. Da der Fuzzyfizierungsprozess auf dem Grad der Zugehörigkeit zu einer Menge basiert, beschreiben die Überlagerungsverfahren die Wechselwirkungen der Ungenauigkeiten in der Zugehörigkeit der Menge. Die Fuzzy-Überlagerungsverfahren basieren auf der Mengenlehre. Die Mengenlehre ist der Teilbereich der Mathematik, der die Zugehörigkeit von Phänomenen zu bestimmten Mengen in Zahlen ausdrückt. Bei "Fuzzy-Überlagerung" entspricht eine Menge i. d. R. einer Klasse.
Die verfügbaren Fuzzy-Mengen-Überlagerungsverfahren sind: "Fuzzy-Und", "Fuzzy-Oder", "Fuzzy-Produkt", "Fuzzy-Summe" und "Fuzzy-Gamma". Jedes dieser Verfahren beschreibt die Zugehörigkeitsbeziehung der Zelle zu den Eingabemengen. Der Überlagerungstyp "Fuzzy-Und" erstellt zum Beispiel ein Ausgabe-Raster, in dem jedem Zellenwert der kleinste zugewiesene Fuzzy-Wert für jede der Mengen, zu denen die Zellenposition gehört, zugewiesen wird. Wenn die Überlagerungsanalyse ein Eignungsmodell zum Wohnen ist und jedes der Mehrfachkriterien relativ zur Zugehörigkeit zu geeigneten Mengen fuzzyfiziert wurde, dann identifiziert "Fuzzy-Und" die niedrigste Wahrscheinlichkeit einer Zugehörigkeit der Zelle zu einer der geeigneten Mengen innerhalb der Mehrfachkriterien.
Der Überlagerungstyp "Fuzzy-Oder" gibt den größten Wert der Schnittmenge der Mengen zurück. Im Eignungsmodell zum Wohnen heißt das, dass die höchste potenzielle Zugehörigkeit (der höchste Eignungswert) für jede Zelle für die Mehrfachkriterien ausgewertet wird.
Binäre, gewichtete und Fuzzy-Logik-Überlagerung
In vielen Beschreibungen der Fuzzy-Logik für die Überlagerungsanalyse wird im Allgemeinen mit der binär-codierten Überlagerungsanalyse verglichen. In der binär-codierten Überlagerungsanalyse wird für jedes Kriterium jede Zelle danach ausgewertet, ob sie Teil einer angegebenen Klasse ist oder nicht. Wie oben erwähnt, kann es in vielen Fällen schwierig sein, klare Klassengrenzen zu definieren und bestimmten Klassen Zellen definitiv zuzuweisen. In einer binär-codierten Analyse bei einem Eignungsmodell zum Wohnen wird für jedes Kriterium jeder Zelle der Wert für geeignet (1) oder nicht geeignet (0) zugewiesen. Im Überlagerungsprozess gelten die Positionen, denen für alle Eingabekriterien eine 1 zugewiesen wurde, als potenziell geeignete Standorte.
Für den Ansatz der binär-codierten Überlagerungsanalyse gelten die folgenden Einschränkungen:
- Wenn keine Position alle Kriterien erfüllt, gibt es keine identifizierte zweitbeste Option.
- Es gibt keine relative Gewichtung der Positionen, die die Kriterien erfüllen.
- Die oben beschriebenen Probleme betreffen den Klassifizierungsprozess.
Die gewichtete Überlagerungsanalyse versucht, diese Einschränkungen zu berücksichtigen. Anstatt jede Zelle auf einer binären Skala mit den Werten 1 und 0 zu klassifizieren, weist das Werkzeug Gewichtete Überlagerung jeden Zellenwert einer definierten kontinuierlichen Skala zu, wie zum Beispiel einer Skala von 1 bis 10, wobei 10 die höchste Präferenz relativ zu den Kriterien darstellt. Die kontinuierliche Skala ermöglicht mehr Abstufungen der Klassen und damit eine stärkere Verfeinerung der Darstellung des Phänomens. Für jedes Kriterium wird jede Zelle der Skala von 1 bis 10 zugewiesen. Danach werden alle reklassifizierten Kriterien zusammenaddiert. Die Zellenpositionen mit den höchsten Summenwerten stellen die höchste Präferenz relativ zu den Kriterien dar. Je besser sich die Kriterien jeder Eingabe eignen, desto besser ist es.
Die Fuzzy-Überlagerung und die gewichtete Überlagerung ähneln einander stärker als sie der binär-codierten Überlagerung ähneln, basieren aber auf verschiedenen Grundlagen. Die Fuzzy-Überlagerung basiert auf der Mengenlehre, die gewichtete Überlagerung dagegen auf linearen Kombinationen. Beide Verfahren transformieren die ursprünglichen Werte. Bei der Fuzzy-Überlagerung definiert die Transformation Möglichkeit der Zugehörigkeit zu Mengen, während die gewichtete Überlagerung mit einer relativen Präferenzskala arbeitet. Da diese zwei Verfahren einzigartig sind, sind die Werkzeuge zum Ausführen von Analysen zwischen mehreren Kriterien nicht austauschbar.
Fuzzy-Logik und der Prozess der allgemeinen Überlagerungsanalyse
Bei der Überlagerungsanalyse "Fuzzy-Logik" werden die allgemeinen Überlagerungsanalyse-Schritte befolgt. Allerdings liegt der Schwerpunkt mehr auf bestimmten Schritten, auf anderen dagegen weniger. Außerdem haben die Werte der zugewiesenen Zahlen eine andere Bedeutung als bei den anderen Überlagerungsanalyseansätzen.
Die allgemeinen Überlagerungsanalyse-Schritte sind:
- Definieren Sie das Problem.
- Gliedern Sie das Problem in untergeordnete Modelle.
- Bestimmen Sie wichtige Layer.
- Reklassifizieren oder transformieren Sie die Daten innerhalb eines Layers.
- Gewichten Sie die Eingabe-Layer.
- Addieren oder kombinieren Sie die Layer.
- Führen Sie die Analyse durch.
Wie bei allen Überlagerungsanalysen sind die Schritte 1 bis 3 für die Fuzzy-Logik-Analyse dieselben. Da Fuzzy-Logik auf Mengen basiert, machen die Bedeutung der reklassifizierten Werte (Schritt 4) und die Analyseverfahren, die zum Kombinieren der Mehrfachkriterien verwendet werden können (Schritt 6), die Fuzzy-Logik im Vergleich zu anderen Überlagerungsanalyseansätzen zu einem einzigartigen Verfahren.
In den folgenden Abschnitten wird beschrieben, wie sich Fuzzy-Logik in den Schritten 4 bis 7 unterscheidet.
Reklassifizieren oder Transformieren der Daten innerhalb eines Layers
Die Eingabedaten werden entsprechend der Möglichkeit der Zugehörigkeit zu einer angegebenen Menge in eine Skala von 0 bis 1 reklassifiziert oder transformiert. Dieser Reklassifizierungs- oder Fuzzyfizierungsprozess wird über das Werkzeug Fuzzy-Zugehörigkeit implementiert. Zur Unterstützung in diesem Transformationsprozess wurde eine Reihe von Zugehörigkeitsfunktionen entwickelt. Die verfügbaren Funktionen sind: "Gauß'sche Fuzzy-Zugehörigkeit", "Fuzzy-Groß", "Fuzzy-Linear", "Fuzzy-MSLarge", "Fuzzy-MSSmall", "Fuzzy-Nah" und "Fuzzy-Klein". Jede Zugehörigkeitsfunktion transformiert die Daten mit einer bestimmten Methode, um die Wechselwirkungen des Phänomens zu erfassen.
Gewichten der Eingabe-Layer
Da Fuzzy-Logik auf der Mengenlehre basiert und Sie bestimmen, ob eine bestimmte Position zu einer oder mehreren Mengen gehört, ist eine Gewichtung nicht sinnvoll. Durch Erhöhung der Gewichtung des einen Faktors gegenüber einem anderen Faktor kann die Möglichkeit der Zugehörigkeit zu einer Menge oder einer Kombination mehrerer Mengen nicht erhöht werden. Die Position ist entweder ein Element einer Menge oder nicht (neben allen Graden dazwischen). In der Fuzzy-Überlagerungsanalyse können die Kriterien nicht gewichtet werden.
Addieren oder Kombinieren der Layer
Im Schritt zum Addieren oder Kombinieren analysiert die Fuzzy-Logik die Wechselwirkungen der Möglichkeit einer Zugehörigkeit des Phänomens zu mehreren Mengen. Im Gegensatz dazu basieren die gewichtete Überlagerung und die gewichtete Summe auf der Idee, dass besser geeignete Elemente zu einem besseren Ergebnis führen.
Für die Fuzzy-Überlagerung gibt es bestimmte Verfahren zum Untersuchen dieser relativen Beziehung und zum Quantifizieren der Wechselwirkungen. Die Kombinationsansätze sind: "Fuzzy-Und", "Fuzzy-Oder", "Fuzzy-Produkt", "Fuzzy-Summe" und "Fuzzy-Gamma". Jeder dieser Ansätze basiert auf der Mengenlehre und ist speziell für die Fuzzy-Überlagerungsanalyse vorgesehen.
Analysieren
Wie bei jeder Überlagerungsanalyse ist es Ihre Aufgabe, die Ergebnisse zu analysieren und auszuwerten. Aufgrund der unterschiedlichen Bedeutungen der reklassifizierten Werte und der Überlagerungsverfahren, die den einzelnen Überlagerungsansätzen zugrunde liegen, müssen jedoch möglicherweise verschiedene Mechanismen zur Messung der Gültigkeit der Ergebnisse eingesetzt werden.