Modellierung von räumlichen Beziehungen

Dieses Dokument enthält zusätzliche Informationen zu Werkzeugparametern und eine Einführung in grundlegende Terminologie und Begriffe, die beim Analysieren von Daten mithilfe der Werkzeuge in der Toolbox "Spatial Statistics" wichtig sind. Verwenden Sie dieses Dokument als Referenz, wenn Sie weitere Informationen zu Werkzeugparametern benötigen.

Hinweis:

• Die Werkzeuge in der Toolbox "Spatial Statistics" können nicht direkt mit XY-Ereignis-Layern verwendet werden. Verwenden Sie vor dem Ausführen der Analyse zunächst Features kopieren zum Konvertieren der XY-Ereignisdaten in eine Feature-Class.
• Denken Sie beim Verwenden von Shapefiles daran, dass diese keine NULL-Werte speichern können. Werkzeuge oder andere Verfahren zur Erstellung von Shapefiles aus Nicht-Shapefile-Eingaben speichern oder interpretieren NULL-Werte möglicherweise als Wert 0. In manchen Fällen werden NULL-Werte in Shapefiles als sehr große negative Werte gespeichert. Dies kann zu unerwarteten Ergebnissen führen. Weitere Informationen finden Sie unter Überlegungen zur Geoverarbeitung für die Shapefile-Ausgabe.

Konzeptualisierung von räumlichen Beziehungen

Ein wichtiger Unterschied zwischen räumlichen und herkömmlichen (lageunabhängigen oder nicht räumlichen) Statistiken besteht darin, dass bei den räumlichen Statistiken Raum und räumliche Beziehungen direkt in die Mathematik integriert sind. Infolgedessen müssen Sie bei vielen Werkzeugen der Toolbox "Spatial Statistics" vor der Analyse einen Wert für den Parameter Konzeptualisierung von räumlichen Beziehungen auswählen. Allgemeine Konzeptualisierungen umfassen inverse Entfernung, Fahrzeit, feste Entfernung, nächste Nachbarn (K) und Nachbarschaft. Die verwendete Konzeptualisierung räumlicher Beziehungen ist davon abhängig, was gemessen wird. Wenn Sie die Cluster-Bildung einer bestimmten Art einer samenverbreitenden Pflanze messen, bietet sich die inverse Entfernung an. Wenn Sie jedoch die geographische Verteilung von Pendlern in einer Region bewerten, sind Fahrzeit oder Reisekosten möglicherweise besser zum Beschreiben dieser räumlichen Beziehungen geeignet. Bei manchen Analysen sind Raum und Zeit vielleicht weniger wichtig als abstraktere Begriffe wie Vertrautheit (je vertrauter etwas ist, desto funktional näher ist es) oder räumliche Interaktion (zwischen Los Angeles und New York gibt es beispielsweise viel mehr Telefonanrufe als zwischen New York und einer Kleinstadt in der Nähe von New York, z. B. Poughkeepsie; man könnte daher argumentieren, dass sich Los Angeles und New York funktional näher sind).

Das Werkzeug Räumlich eingeschränkte multivariate Cluster-Bildung enthält den Parameter Räumliche Einschränkungen. Dessen Parameteroptionen ähneln zwar denen, die für den Parameter Konzeptualisierung von räumlichen Beziehungen beschrieben sind, doch werden sie unterschiedlich verwendet. Wenn eine räumliche Einschränkung vorgegeben wird, können nur Features, die mindestens einen Nachbarn gemeinsam haben (definiert durch Nachbarschaft, Beziehungen vom Typ "Nächste Nachbarn" oder Triangulationsmethoden), zu derselben Gruppe gehören. Weitere Informationen und Beispiele finden Sie unter Funktionsweise des Werkzeugs "Räumlich eingeschränkte multivariate Cluster-Bildung".

Die Optionen für den Parameter Konzeptualisierung von räumlichen Beziehungen werden nachfolgend erläutert. Durch die Option, die Sie auswählen, werden die Nachbarbeziehungen für Werkzeuge bestimmt, die jedes Feature innerhalb des Kontexts benachbarter Features bewerten. Diese Werkzeuge umfassen die Werkzeuge Räumliche Autokorrelation (Global Morans I), Hot-Spot-Analyse (Getis-Ord Gi*) und Cluster- und Ausreißeranalyse (Anselin Local Morans I). Beachten Sie, dass einige dieser Optionen nur dann verfügbar sind, wenn Sie das Werkzeug Räumliche Gewichtungsmatrix erstellen verwenden.

Inverse Entfernung, inverse Entfernung im Quadrat (Impedanz)

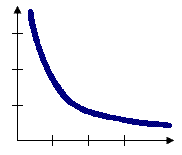
Bei Auswahl der Optionen für die inverse Entfernung handelt es sich bei dem Konzeptmodell für räumliche Beziehungen um ein impedanzbasiertes bzw. entfernungsabhängiges Modell. Alle Features beeinflussen alle anderen Features, je größer jedoch die Entfernung ist, desto geringer sind die Auswirkungen. Sie werden im Allgemeinen einen Wert für Entfernungsband oder Schwellenwertentfernung angeben, wenn Sie eine inverse Entfernungskonzeptualisierung verwenden, um die Anzahl der erforderlichen Berechnungen, besonders bei großen Datasets, zu reduzieren. Wenn kein Wert für das Entfernungsband oder die Schwellenwertentfernung angegeben wird, wird ein Standardschwellenwert für Sie berechnet. Sie können erzwingen, dass alle Features ein Nachbar aller anderen Features werden, indem Sie den Wert für Entfernungsband oder die Schwellenwertentfernung auf null festlegen.

Die inverse euklidische Entfernung ist für das Modellieren kontinuierlicher Daten, z. B. Temperaturschwankungen, geeignet. Die inverse Manhattan-Entfernung funktioniert am besten, wenn die Analyse Standorte von festen städtischen Einrichtungen wie z. B. Baumärkten betrifft, im Fall dass keine Straßennetzdaten verfügbar sind. Das Konzeptmodell bei Verwendung der Option Inverse Entfernung im Quadrat ist dasselbe wie bei Inverse Entfernung, jedoch ist hier die Neigung stärker und der Einfluss von Nachbarn fällt daher schneller ab: Nur der nächste Nachbar eines Ziel-Features kann wesentlichen Einfluss auf die Berechnungen für dieses Feature ausüben.

Entfernungsband (Einflusszone)

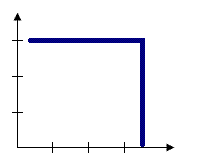
Bei einigen Werkzeugen, z. B. Hot-Spot-Analyse, ist ein festes Entfernungsband die standardmäßige Konzeptualisierung von räumlichen Beziehungen. Mit der Option Festes Entfernungsband wird die Analyse der Daten anhand eines Konzeptmodells für räumliche Beziehungen mit Einflusszone, d. h. mit einem beweglichen Analysefenster, durchgeführt. Jedes Feature wird innerhalb des Kontexts der benachbarten Features analysiert, die sich innerhalb der Entfernung befinden, die Sie für Entfernungsband oder Schwellenwertentfernung angeben. Nachbarn innerhalb der angegebenen Entfernung werden gleich gewichtet. Features außerhalb der angegebenen Entfernung beeinflussen die Berechnungen nicht (ihre Gewichtung ist null). Verwenden Sie die Methode Festes Entfernungsband, wenn Sie die statistischen Eigenschaften Ihrer Daten bei einem bestimmten (festen) Maßstab berechnen möchten. Wenn Sie Pendelmuster untersuchen und wissen, dass die durchschnittliche Fahrtdauer zur Arbeit beispielsweise 15 Kilometer beträgt, können Sie eine feste Entfernung von 15 Kilometern für die Analyse verwenden. Unter Auswählen eines Wertes für ein festes Entfernungsband finden Sie Strategien, mit deren Hilfe Sie einen geeigneten Maßstab für die Analyse ermitteln können.

Indifferenzzone

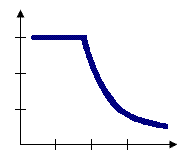
Die Option Indifferenzzone für den Parameter Konzeptualisierung von räumlichen Beziehungen kombiniert die Modelle Festes Entfernungsband und Inverse Entfernung. Features innerhalb des Entfernungsbands oder der Schwellenwertentfernung sind in Analysen für das Ziel-Feature enthalten. Sobald die kritische Entfernung überschritten wird, fällt die Einflussebene (die Gewichtung) schnell ab. Angenommen, Sie suchen nach einem Job und haben die Wahl zwischen einem Job in fünf Kilometern Entfernung und einem Job in sechs Kilometern Entfernung. Bei der Entscheidung, welcher Job der richtige ist, werden Sie wahrscheinlich nicht viel über die Entfernung nachdenken. Nehmen wir nun an, Sie haben die Wahl zwischen einem Job in fünf Kilometern Entfernung und einem Job in 20 Kilometern Entfernung. In diesem Fall wird der Entfernung eine höhere Impedanz zugeordnet, wodurch sie ggf. bei der Entscheidungsfindung berücksichtigt wird. Verwenden Sie diese Methode, wenn Sie den Maßstab der Analyse fixiert halten möchten, die benachbarten Features, die in den Berechnungen der Ziel-Features enthalten sind, aber keinen zu engen Begrenzungen unterwerfen möchten.

Polygonnachbarschaft (erste Ordnung)

Bei Polygon-Feature-Classes können Sie Nur Kontiguitätskanten (auch als "Rook's Case" bezeichnet) oder Kontiguitätsecken und -kanten (auch als "Queen's Case" bezeichnet) wählen. Bei Nur Kontiguitätskanten werden Polygone, die eine gemeinsame Kante (lagegleiche Grenzen) haben, in Berechnungen für das Zielpolygon einbezogen. Polygone, die keine gemeinsame Kante haben, werden aus den Berechnungen für das Ziel-Feature ausgeschlossen. Bei benachbarten Kanten/Ecken werden Polygone, die eine gemeinsame Kante oder Ecke haben, in Berechnungen für das Zielpolygon einbezogen. Wenn sich beliebige Teile der beiden Polygone überlappen, werden diese als Nachbarn betrachtet und in die jeweiligen Berechnungen einbezogen. Verwenden Sie eine dieser Nachbarschaftskonzeptualisierungen mit Polygon-Features, wenn Sie einen benachbarten Prozess modellieren oder mit kontinuierlichen Daten arbeiten, die als Polygone dargestellt werden.

Nächste Nachbarn (K)

Nachbarbeziehungen können auch so erstellt werden, dass jedes Feature im räumlichen Kontext einer angegebenen Anzahl an nächsten Nachbarn bewertet wird. Wenn K (die Anzahl der Nachbarn) 8 beträgt, werden die acht nächsten Nachbarn des Ziel-Features in die Berechnungen für dieses Feature eingeschlossen. An Orten, an denen die Feature-Dichte hoch ist, ist der räumliche Kontext der Analyse kleiner. In ähnlicher Weise ist der räumliche Kontext für die Analyse an Orten, an denen die Feature-Dichte niedrig, größer. Ein Vorteil dieses Modells räumlicher Beziehungen besteht darin, dass dadurch sichergestellt wird, dass für jedes Ziel-Feature Nachbarn vorhanden sind, auch dann, wenn die Feature-Dichte über das Untersuchungsgebiet hinweg stark variiert. Diese Methode ist über das Werkzeug Räumliche Gewichtungsmatrix erstellen verfügbar. Die Option Nächste Nachbarn (K) mit 8 als Anzahl der Nachbarn ist die Standardkonzeptualisierung, die mit der Regressionsanalyse zum Bewerten von Regressionsresiduen verwendet wird.

Delaunay-Triangulation (natürliche Nachbarn)

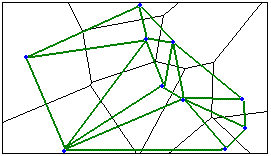
Mit der Option "Delaunay-Triangulation" werden Nachbarn erstellt, indem Voronoi-Dreiecke aus Punkt-Features oder Feature-Schwerpunkten erstellt werden, sodass jeder Punkt oder Schwerpunkt ein Dreiecksknoten ist. Knoten, die über eine Dreieckskante verbunden sind, werden als Nachbarn betrachtet. Mit der Delaunay-Triangulation kann sichergestellt werden, dass jedes Feature mindestens einen Nachbarn hat, auch dann, wenn in den Daten Inseln oder stark variierende Feature-Dichten vorliegen. Verwenden Sie die Option für die Delaunay-Triangulation nicht bei lagegleichen Features. Diese Methode ist über das Werkzeug Räumliche Gewichtungsmatrix erstellen verfügbar.

Raum-Zeit-Fenster

Mit dieser Option definieren Sie Feature-Beziehungen für ein Raum- (feste Entfernung) und ein Zeitfenster (festes Zeitintervall). Diese Option ist verfügbar, wenn Sie mit dem Werkzeug Räumliche Gewichtungsmatrix erstellen eine Datei mit einer räumlichen Gewichtungsmatrix erstellen. Wenn Sie Raum-Zeit-Fenster auswählen, müssen Sie ein Datums-/Uhrzeitfeld, einen Intervalltyp von Datum/Uhrzeit (beispielsweise Stunden, Tage oder Monate) sowie einen Intervallwert von Datum/Uhrzeit angeben. Der Intervallwert ist eine Ganzzahl. Wenn Sie zum Beispiel als Intervalltyp Stunden und als Intervallwert 3 ausgewählt haben, werden zwei Features als Nachbarn betrachtet, wenn sich die Werte in deren Datums-/Uhrzeitfeld um maximal drei Stunden unterscheiden. Bei Verwendung dieser Konzeptualisierung sind Features Nachbarn, wenn sie innerhalb der angegebenen Entfernung und zudem innerhalb des angegebenen Zeitintervalls des Ziel-Features liegen. Sie wählen beispielsweise für Konzeptualisierung von räumlichen Beziehungen die Option Raum-Zeit-Fenster aus, wenn Sie eine Datei mit räumlicher Gewichtungsmatrix erstellen möchten, um mit Hot Spot-Analyse Raum-Zeit-Hot-Spots zu ermitteln. Weitere Informationen, unter anderem zum Visualisieren der Ergebnisse, finden Sie im Thema Raum/Zeit-Analysen. Zum besseren Visualisieren eines netCDF-Raum-Zeit-Würfels in 3D sind weitere Möglichkeiten verfügbar.

Abrufen von räumlichen Gewichtungen aus Datei (benutzerdefinierte räumliche Beziehungen)

Mithilfe des Werkzeugs Räumliche Gewichtungsmatrix erstellen können Sie auch eine Datei zum Speichern von Nachbarbeziehungen für Features erstellen. Wenn die räumlichen Beziehungen für die Features in einer Tabelle definiert sind, können Sie das Werkzeug "Räumliche Gewichtungsmatrix erstellen" verwenden, um diese Tabelle in eine Datei mit einer räumlichen Gewichtungsmatrix (.swm-Datei) zu konvertieren. Um mit der Option Tabelle konvertieren eine SWM-Datei zu erhalten, müssen bestimmte Felder in die Tabelle aufgenommen werden. Sie können auch einen Pfad zu einer formatierten ASCII-Textdatei bereitstellen, in der eine eigene benutzerdefinierte Konzeptualisierung räumlicher Beziehungen (beispielsweise auf Grundlage von räumlichen Wechselwirkungen) definiert wird.

Empfehlungen für die Auswahl einer Konzeptualisierung räumlicher Beziehungen

Je realistischer Sie modellieren können, wie Features im Raum interagieren, desto genauer werden die Ergebnisse. Ihre Auswahl für den Parameter Konzeptualisierung von räumlichen Beziehungen sollte inhärente Beziehungen unter den Features, die analysiert werden, widerspiegeln. Manchmal wird die Auswahl auch von Eigenschaften der Daten beeinflusst.

Die Methoden zur Berechnung inverser Entfernungen (Inverse Entfernung und Inverse Entfernung im Quadrat) beispielsweise eignen sich am besten für kontinuierliche Daten oder zum Modellieren von Prozessen, bei denen die Wahrscheinlichkeit, dass Features in Wechselwirkung stehen bzw. einander beeinflussen, umso größer ist, je näher diese beiden Features räumlich beieinander liegen. Bei dieser räumlichen Konzeptualisierung ist jedes Feature potenziell ein Nachbar jedes anderen Features, bei großen Datasets ist die Anzahl der beteiligten Berechnungen sehr hoch. Bei Verwendung der inversen Entfernungskonzeptualisierung sollten Sie immer versuchen, einen Wert für Entfernungsband oder Schwellenwertentfernung einzuschließen. Dies ist für große Datasets besonders wichtig. Wenn Sie den Parameter Entfernungsband oder Schwellenwertentfernung leer lassen, wird eine Schwellenwertentfernung für Sie berechnet. Es kann jedoch sein, dass dies nicht die angemessene Entfernung für die Analyse ist. Der standardmäßige Entfernungsschwellenwert ist die minimale Entfernung, bei der sichergestellt wird, dass das Feature mindestens einen Nachbarn hat.

Die Methode Festes Entfernungsband ist für Punktdaten gut geeignet. Sie ist die vom Werkzeug Hot-Spot-Analyse (Getis-Ord Gi*) verwendete Standardoption. Häufig ist sie auch eine gute Option, wenn Polygondaten hinsichtlich der Polygongröße stark variieren (z. B. sehr große Polygone am Rand des Untersuchungsgebiets und sehr kleine Polygone in der Mitte des Untersuchungsgebiets) und Sie einen einheitlichen Analysemaßstab sicherstellen möchten. Unter Auswählen eines Wertes für ein festes Entfernungsband weiter unten finden Sie Strategien, mit deren Hilfe Sie einen geeigneten Entfernungsbandwert für die Analyse ermitteln können.

Die Konzeptualisierung Indifferenzzone funktioniert gut, wenn sich eine feste Entfernung anbietet, jedoch durch scharfe Grenzen für Nachbarschaftsbeziehungen keine genaue Darstellung Ihrer Daten erreicht wird. Bedenken Sie, dass bei dem Konzeptmodell der Indifferenzzone jedes Feature als Nachbar jedes anderen Features betrachtet wird. Diese Option ist daher nicht für große Datasets geeignet, da der angegebene Wert für Entfernungsband oder Schwellenwertentfernung die Anzahl der Nachbarn nicht einschränkt, sondern nur angibt, wo die Intensität von räumlichen Beziehungen abzunehmen beginnt.

Die Konzeptualisierungen für Polygonnachbarschaft (Nur benachbarte Kanten und Benachbarte Kanten/Ecken) sind hilfreich, wenn Polygone im Hinblick auf Größe und Verteilung ähnlich sind und räumliche Beziehungen eine Funktion der Polygonnachbarschaft sind (hierbei wird angenommen, dass die räumlichen Wechselwirkungen zwischen zwei Polygonen zunehmen, wenn diese eine gemeinsame Kante haben). Wenn Sie eine Konzeptualisierung der Polygonnachbarschaft auswählen, möchten Sie wahrscheinlich fast immer eine Zeilenstandardisierung für Werkzeuge auswählen, die über den Parameter Zeilenstandardisierung verfügen.

Die Option Nächste Nachbarn (K) ist hilfreich, wenn Sie sicherstellen möchten, dass eine minimale Anzahl von Nachbarn für die Analyse verfügbar ist. Insbesondere, wenn die mit den Features verknüpften Werte verzerrt (nicht normal verteilt) sind, ist es wichtig, dass jedes Feature im Kontext von mindestens acht Nachbarn ausgewertet wird (dies ist nur eine Faustregel). Wenn die Verteilung der Daten im Untersuchungsgebiet so variiert, dass sich einige Features sehr weit von allen anderen Features befinden, bietet sich diese Methode an. Beachten Sie jedoch, dass sich der räumliche Kontext der Analyse in Abhängigkeit von Variationen im Hinblick auf Seltenheit bzw. Dichte der Features ändert. Wenn das Fixieren des Analysemaßstabs weniger wichtig als das Fixieren der Anzahl von Nachbarn ist, bietet sich die Methode "Nächste Nachbarn (K)" an.

Einige Analysten betrachten die Option der Delaunay-Triangulation als eine Möglichkeit zur Erstellung natürlicher Nachbarn für einen Satz von Features. Dies bietet sich an, wenn die Daten Inselpolygone (isolierte Polygone, die keine gemeinsamen Kanten mit anderen Polygonen haben) enthalten oder eine sehr ungleichmäßige räumliche Verteilung von Features vorliegt. Bei lagegleichen Features ist sie jedoch nicht geeignet. Durch die Delaunay-Triangulation wird, ähnlich wie bei der Methode "Nächste Nachbarn (K)", sichergestellt, dass jedes Feature mindestens einen Nachbarn hat, jedoch die Verteilung der Daten selbst verwendet wird, um zu bestimmen, wie viele Nachbarn jedes Feature erhält.

Mit der Option Raum-Zeit-Fenster können Sie Feature-Beziehungen in Hinblick auf räumliche und zeitliche Nähe definieren. Verwenden Sie diese Option zum Ermitteln von Raum-Zeit-Hot-Spots oder Erstellen von Gruppen, in denen die Mitgliedschaft durch räumliche und zeitliche Nähe eingeschränkt wird. Beispiele für Raum-Zeit-Analysen sowie Strategien für das effektive Rendering der Ergebnisse solcher Analysen finden Sie im Thema Raum/Zeit-Analysen.

Für einige Anwendungen kann die räumliche Interaktion am besten im Hinblick auf Fahrzeit oder Reisestrecke modelliert werden. Wenn Sie beispielsweise die Zugänglichkeit zu städtischen Diensten modellieren oder nach Orten mit hoher Kriminalität suchen, ist die Modellierung räumlicher Beziehungen hinsichtlich eines Netzwerks eine gute Wahl. Erstellen Sie vor der Analyse mit dem Werkzeug Räumliche Gewichtung des Netzwerks generieren eine Datei mit räumlicher Gewichtungsmatrix (.swm). Wählen Sie GET_SPATIAL_WEIGHTS_FROM_FILE als Wert für Konzeptualisierung von räumlichen Beziehungen aus, und geben Sie für den Parameter Gewichtungsmatrix-Datei den vollständigen Pfad zu der erstellten SWM-Datei an.

Tipp:

Viele Organisationen verwalten ihre eigenen Straßennetz-Datasets, auf die Sie bereits zugreifen können. Alternativ beinhaltet StreetMap Premium for ArcGIS vordefinierte Netzwerk-Datasets im SDC-Format, die Nordamerika, Lateinamerika, Europa, den Nahen Osten, Afrika, Japan, Australien und Neuseeland abdecken. Diese Netzwerk-Datasets können von diesem Werkzeug direkt verwendet werden.

Wenn keine der Optionen des Parameters Konzeptualisierung von räumlichen Beziehungen für Ihre Analyse geeignet ist, können Sie eine ASCII-Textdatei oder eine Tabelle mit den gewünschten Feature-zu-Feature-Beziehungen erstellen. Verwenden Sie diese dann zum Erstellen einer Datei mit räumlicher Gewichtungsmatrix. Wenn sich eine der obigen Optionen im Prinzip für Ihre Zwecke eignet, aber nicht ganz optimal ist, können Sie mit dem Werkzeug Räumliche Gewichtungsmatrix erstellen eine einfache SWM-Datei erstellen und dann die Datei mit räumlicher Gewichtungsmatrix bearbeiten.

Entfernungsmethode

Viele der Werkzeuge in der Toolbox "Spatial Statistics" verwenden Entfernungen in ihren Berechnungen. Bei diesen Werkzeugen können Sie entweder die euklidische oder die Manhattan-Entfernung auswählen.

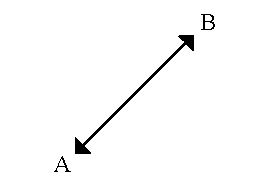
• Die euklidische Entfernung wird berechnet als

D = Quadratwurzel [(x1–x2)**2,0 + (y1–y2)**2,0]

wobei (x1, y1) die Koordinate für Punkt A, (x2, y2) die Koordinate für Punkt B und D die geradlinige Entfernung zwischen Punkt A und Punkt B ist.

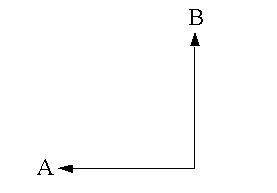
• Die Manhattan-Entfernung wird berechnet als

D = abs(x1–x2) + abs(y1–y2)

wobei (x1, y1) die Koordinate für Punkt A, (x2, y2) die Koordinate für Punkt B und D die vertikale plus horizontale Differenz zwischen Punkt A und Punkt B ist. Diese Entfernung müssen Sie zurücklegen, wenn Sie auf Reisen von Norden nach Süden und von Osten nach Westen beschränkt sind. Diese Methode passt im Allgemeinen besser als die euklidische Entfernung, wenn Reisen auf ein Straßennetz beschränkt sind und tatsächliche Reisekosten für das Straßennetz nicht verfügbar sind.

Wenn die Eingabe-Features nicht projiziert sind (d. h., wenn Kandidaten in Grad, Minuten und Sekunden angegeben werden), als Ausgabekoordinatensystem ein geographisches Koordinatensystem festgelegt wird oder Sie einen Ausgabe-Feature-Class-Pfad zu einem Feature-Dataset mit geographischem Koordinatensystem als Raumbezug angeben, werden die Entfernungen mit Sehnenmesswerten berechnet. Der Parameter Entfernungsmethode wird dabei deaktiviert. Sehnenentfernungsmesswerte werden verwendet, weil sie schnell berechnet werden können und ausgezeichnete Schätzungen von echten geodätischen Entfernungen zulassen, zumindest für Punkte innerhalb von 30 Grad voneinander. Sehnenentfernungen basieren auf einer Kugel anstelle der abgeplatteten Ellipsenform der Erde. Im Fall von zwei beliebigen Punkten auf der Erdoberfläche ist die Sehnenentfernung zwischen diesen die Länge einer Linie, die durch die dreidimensionale Erde führt, um diese beiden Punkte zu verbinden. Sehnenentfernungen werden in Metern angegeben.

Vorsicht:

Achten Sie darauf, Ihre Daten zu projizieren, wenn sich der Untersuchungsbereich über 30 Grad hinaus erstreckt. Sehnenentfernungen erlauben keine sichere Schätzung von geodätischen Entfernungen über 30 Grad hinaus.

Eigenpotenzial (Feld, das eine intrazonale Gewichtung verleiht)

Bei mehreren Werkzeugen in der Toolbox "Spatial Statistics" können Sie ein Feld angeben, das die für das Eigenpotenzial zu verwendende Gewichtung darstellt. Eigenpotenzial ist die Entfernung oder die Gewichtung zwischen einem Feature und sich selbst. Oft ist diese Gewichtung null. In manchen Fällen möchten Sie jedoch eventuell einen anderen festen Wert oder einen unterschiedlichen Wert für jedes Feature angeben. Wenn die Konzeptualisierung von räumlichen Beziehungen auf Entfernungen basiert, die innerhalb und zwischen Zählbezirken zurückgelegt werden, können Sie beispielsweise das Eigenpotenzial modellieren, um die durchschnittlichen intrazonalen Reisekosten basierend auf der Polygongröße widerzuspiegeln:

dii = 0,5*[(Ai / π)**0,5]

wobei di_i die Reisekosten sind, die mit der intrazonalen Reise für das Polygon-Feature_i verknüpft sind, und A_i die mit dem Polygon-Feature_i verknüpfte Fläche ist.

Standardisierung

Eine Reihen-Standardisierung wird immer dann empfohlen, wenn die Verteilung der Features aufgrund einer Referenzpunkterfassung oder eines auferlegten Zusammenfassungsschemas möglicherweise verzerrt ist. Wenn die Zeilenstandardisierung ausgewählt wird, wird jede Gewichtung durch ihre eigene Zeilensumme (die Summe der Gewichtungen aller benachbarten Features) dividiert. Eine zeilenstandardisierte Gewichtung wird häufig bei Nachbarschaften mit festen Entfernungen und fast immer bei Nachbarschaften basierend auf Polygonnachbarschaft verwendet. Dadurch soll die Verzerrung aufgrund von Features mit einer unterschiedlichen Anzahl von Nachbarn abgeschwächt werden. Durch eine Zeilenstandardisierung werden alle Gewichtungen so skaliert, dass sie zwischen 0 und 1 liegen; dadurch wird ein relatives (und kein absolutes) Gewichtungsschema geschaffen. Wenn Sie mit Polygon-Features arbeiten, die Verwaltungsgrenzen darstellen, möchten Sie eventuell die Option "Zeilenstandardisierung" auswählen.

Nachfolgend finden Sie einige Beispiele:

• Angenommen, Sie verfügen über einen vollständigen Satz aller Verbrechensfälle. In einigen Teilen Ihres Untersuchungsgebiets gibt es zahlreiche Punkte, das dies Gebiete mit hoher Anzahl von Verbrechen sind. In anderen Teilen gibt es wenige Punkte, da in diesen Gebieten nur wenige Verbrechen verübt wurden. Die Dichte der Punkte gibt sehr gut wieder (ist repräsentativ dafür), was Sie zu verstehen suchen: das räumliche Muster der Verbrechen. Es empfiehlt sich wahrscheinlich nicht, die räumlichen Gewichtungen zu reihenstandardisieren.
• Angenommen, Sie verfügen über Bodenproben. Aus einem beliebigen Grund (das Wetter war schön oder Sie waren an einem Ort, an dem Sie keine Zäune überwinden, Sümpfe durchschwimmen oder Berge besteigen mussten) haben Sie zahlreiche Proben von bestimmten Teilen des Untersuchungsgebiets, aber wenige Proben von anderen Teilen. Anders gesagt, ist die Dichte der Punkte nicht gerade das Ergebnis einer sorgfältig geplanten Zufallsstichprobe, Sie haben wohl selbst einige Verzerrungen verursacht. Zudem geben die Bereiche mit mehr Punkten nicht notwendigerweise die zugrunde liegende räumliche Verteilung der zu analysierenden Daten wieder. Um die Verzerrungen zu minimieren, die Sie möglicherweise bei der Stichprobennahme verursacht haben, können Sie die räumlichen Gewichtungen reihenstandardisieren. Nach einer Reihen-Standardisierung wirkt sich der Umstand, dass ein Feature 2 Nachbarn und ein anderes 18 hat, nicht mehr stark auf die Ergebnisse aus – alle Gewichtungen ergeben die Summe 1.
• Beim Aggregieren der Daten wenden Sie auf diese eine Struktur an. Diese Struktur gibt die zu analysierenden Daten und die gestellten Fragen nur selten gut wieder. Beispielsweise werden Bevölkerungszählungs-Polygone (z. B. Zählbezirke) anhand der Bevölkerung konzipiert, aber selbst wenn Ihre Analyse bevölkerungsrelevante Fragen umfasst, empfiehlt es sich meist, die Gewichtungen zu reihenstandardisieren, da diese Polygone nur einer von vielen Darstellungsmöglichkeiten entsprechen. Bei Polygondaten sollten Sie fast immer die Reihen-Standardisierung auf die räumlichen Gewichtungen anwenden.

Entfernungsband oder Schwellenwertentfernung

Entfernungsband oder Schwellenwertentfernung legt den Analysemaßstab für die meisten Konzeptualisierungen von räumlichen Beziehungen (z. B. inverse Entfernung und festes Entfernungsband) fest. Es handelt sich dabei um einen positiven Zahlenwert, der einen Entfernungsgrenzwert darstellt. Features außerhalb des angegebenen Grenzwertes für ein Ziel-Feature werden in der Analyse für dieses Feature ignoriert. Mit Indifferenzzone wird jedoch der Einfluss von Features außerhalb der angegebenen Entfernung im Verhältnis zur Nähe reduziert, während die Features innerhalb des Entfernungsschwellenwertes gleichmäßig berücksichtigt werden.

Es ist wichtig, dass eine angemessene Entfernung ausgewählt wird. Einige räumliche Statistiken erfordern, dass jedes Feature mindestens einen Nachbarn hat, damit die Analyse zuverlässig ist. Wenn der Wert, den Sie für Entfernungsband oder Schwellenwertentfernung festlegen, zu klein ist (sodass einige Features keine Nachbarn haben), wird eine Warnmeldung angezeigt, in der vorgeschlagen wird, dass Sie es mit einem größeren Entfernungswert erneut versuchen. Das Werkzeug Entfernungsband anhand der Anzahl der Nachbarn berechnen wertet die minimale, durchschnittliche und maximale Entfernung für eine angegebene Anzahl von Nachbarn aus und kann bei der Bestimmung eines geeigneten Wertes für das Entfernungsband helfen, der für die Analyse verwendet werden soll. Weitere Informationen finden Sie unter Auswählen eines Wertes für ein festes Entfernungsband.

Wenn kein Wert angegeben wird, wird eine standardmäßige Schwellenwertentfernung berechnet. In der Tabelle unten ist angegeben, wie sich unterschiedliche Optionen für den Parameter Konzeptualisierung von räumlichen Beziehungen für jede der drei möglichen Eingabetypen verhalten (negative Werte sind nicht gültig):

Optionen für Entfernungsband

	Inverse Entfernung, Inverse Entfernung im Quadrat	Festes Entfernungsband, Indifferenzzone	Polygonnachbarschaft, Delaunay-Triangulation, Nächste Nachbarn (K)
0	Es wird kein Schwellenwert oder Grenzwert angewendet; jedes Feature ist ein Nachbar von jedem anderen Feature.	Ungültig. Ein Laufzeitfehler wird generiert.	Ignoriert.
Leer	Eine Standardentfernung wird berechnet. Dieser Standard ist die minimale Entfernung, bei der sichergestellt wird, dass jedes Feature mindestens einen Nachbarn hat.	Eine Standardentfernung wird berechnet. Dieser Standard ist die minimale Entfernung, bei der sichergestellt wird, dass jedes Feature mindestens einen Nachbarn hat.	Ignoriert.
positive Zahl	Der positive Wert, der nicht null ist, wird als Grenzentfernung verwendet; Nachbarbeziehungen sind nur unter Features innerhalb dieser Entfernung voneinander vorhanden.	Für das feste Entfernungsband sind nur Features innerhalb dieses angegebenen Grenzwertes voneinander Nachbarn. Bei Indifferenzzone sind Features innerhalb der Entfernung dieses angegebenen Grenzwertes voneinander Nachbarn, Features außerhalb des Grenzwertes auch. Diesen wird aber mit zunehmender Entfernung eine kleinere Gewichtung und damit ein geringerer Einfluss zugewiesen.	Ignoriert.

Anzahl der Nachbarn

Geben Sie eine positive Ganzzahl an, um die Anzahl von Nachbarn darzustellen, die in die Analyse für jedes Ziel-Feature eingeschlossen werden soll. Wenn der für die Konzeptualisierung von räumlichen Beziehungen ausgewählte Wert Nächste Nachbarn (K) lautet, wird jedes Ziel-Feature im Kontext der nächsten K Features ausgewertet (wobei K der angegebenen Anzahl an Nachbarn entspricht). Für Inverse Entfernung und Festes Entfernungsband wird beim Ausführen des Werkzeugs Räumliche Gewichtungsmatrix erstellen durch Angabe eines Wertes für den Parameter Anzahl der Nachbarn sichergestellt, dass jedes Feature mindestens K Nachbarn hat. Bei den Methoden für die Polygonnachbarschaft erhält jedes Feature, für das kein Wert für Anzahl der Nachbarn angegeben wurde, zusätzliche Nachbarn basierend auf der Nähe von Feature-Schwerpunkten.

Datei mit Gewichtungsmatrix

Mit einigen Werkzeugen können Sie räumliche Beziehungen unter Features definieren, indem Sie einen Pfad zu einer Datei mit räumlichen Gewichtungsmatrix angeben. Räumliche Gewichtungen sind Zahlen, die die Entfernung, Zeit oder andere Kosten zwischen jedem Feature und allen anderen Features im Dataset widerspiegeln. Die Datei mit räumlicher Gewichtungsmatrix kann mit dem Werkzeug Räumliche Gewichtungsmatrix erstellen erstellt werden. Es kann sich auch um eine einfache ASCII-Datei handeln.

Wenn die Datei mit räumlicher Gewichtungsmatrix eine einfache ASCII-Textdatei ist, sollte die erste Zeile der Name eines eindeutigen ID-Feldes sein. Dies gibt Ihnen die Flexibilität, ein beliebiges Zahlenfeld im Dataset als ID zu verwenden, wenn Sie diese Datei generieren; das ID-Feld muss jedoch vom Typ "Short Integer" oder "Long Integer" sein und Einzelwerte für jedes Feature aufweisen. Nach der ersten Zeile sollte die Datei mit räumlichen Gewichtungen in drei Spalten formatiert werden:

• Quell-Feature-ID
• Ziel-Feature-ID
• Gewichtung

Nehmen wir zum Beispiel an, Sie besitzen drei Tankstellen. Das als ID-Feld verwendete Feld trägt den Namen StationID, und die Feature-IDs lauten 1, 2 und 3. Sie möchten räumliche Beziehungen unter diesen drei Tankstellen mithilfe der Fahrzeit in Minuten modellieren. Sie können eine ASCII-Datei erstellen, die folgendermaßen aussieht:

Wenn Gewichtungen eine Entfernung oder Zeit darstellen, werden sie in der Regel invertiert (z. B. 1/10, wenn die Entfernung 10 Kilometer oder 10 Minuten ist), damit nähere Features eine größere Gewichtung haben als Features, die weiter entfernt sind. Beachten Sie bei den Gewichtungen oben, dass Tankstelle 1 10 Minuten von Tankstelle 2 entfernt ist. Beachten Sie auch, dass die Fahrzeit in diesem Beispiel nicht symmetrisch ist (die Fahrt von Tankstelle 1 zu Tankstelle 3 beträgt 7 Minuten, die Fahrt von Tankstelle 3 zu Tankstelle 1 beträgt jedoch nur 6 Minuten). Die Gewichtung zwischen Tankstelle 1 und sich selbst beträgt 0, und es ist kein Eintrag für die Tankstelle 2 zu sich selbst vorhanden. Bei fehlenden Einträgen wird eine Gewichtung von 0 angenommen.

Das Eingeben der Werte für die Datei mit räumlicher Gewichtungsmatrix ist sehr mühevoll, auch bei kleinen Datasets. Ein besserer Ansatz besteht darin, das Werkzeug Räumliche Gewichtungsmatrix erstellen zu verwenden oder ein kurzes Python-Skript zu schreiben, das diesen Task für Sie ausführt.

Datei mit räumlicher Gewichtungsmatrix (SWM-Datei)

Mit dem Werkzeug Räumliche Gewichtungsmatrix erstellen wird eine Datei mit räumlicher Gewichtungsmatrix (.swm) erstellt, die die räumlichen Beziehungen unter allen Features im Dataset auf Grundlage der angegebenen Parameter definiert. Diese Datei wird in binärem Dateiformat erstellt, sodass die Werte in der Datei nicht direkt angezeigt werden können. Zum Anzeigen oder Bearbeiten der Feature-Beziehungen in einer SWM-Datei verwenden Sie das Werkzeug Räumliche Gewichtungsmatrix in Tabelle konvertieren.

Wenn die räumlichen Beziehungen zwischen den Features in einer Tabelle gespeichert werden, können Sie das Werkzeug Räumliche Gewichtungsmatrix erstellen verwenden, um diese Tabelle in eine .swm-Datei zu konvertieren. Die Tabelle benötigt die folgenden Felder:

Erforderliche Tabellenfelder

Feldname	Beschreibung
<Eindeutiger ID-Feldname>	Ein Ganzzahlfeld, das in der Eingabe-Feature-Class mit einer eindeutigen ID für jedes Feature vorhanden ist. Dies ist die Quell-Feature-ID.
NID	Ein Ganzzahlfeld, das die Feature-IDs der Nachbarn enthält. Dies ist die Ziel-Feature-ID.
GEWICHTUNG	Dies ist die numerische Gewichtungsquantifizierung der räumlichen Beziehung zwischen den Quell- und Ziel-Features. Größere Werte spiegeln größere Gewichtungen und stärkeren Einfluss bzw. Interaktion zwischen zwei Features wider.

Freigeben von Dateien mit räumlicher Gewichtungsmatrix

Die Ausgabe des Werkzeugs Räumliche Gewichtungsmatrix erstellen ist eine SWM-Datei. Diese Datei wird beim Erstellen mit der Eingabe-Feature-Class, dem eindeutigen ID-Feld und den Einstellungen für das Ausgabe-Koordinatensystem verknüpft. Andere Personen können die räumlichen Beziehungen duplizieren, die Sie für die Analyse definieren, indem sie die SWM-Datei zusammen mit derselben Eingabe-Feature-Class bzw. einer Feature-Class, die alle oder eine Teilmenge der Features mit einem passenden Unique ID-Feld verknüpft, verwenden. Insbesondere, wenn Sie planen, die SWM-Dateien für andere freizugeben, sollten Sie versuchen, Situationen zu vermeiden, in denen sich das Ausgabe-Koordinatensystem von dem Raumbezug unterscheidet, der mit der Eingabe-Feature-Class verknüpft ist. Eine bessere Strategie besteht darin, die Eingabe-Feature-Class zu projizieren und vor dem Erstellen der SWM-Dateien das Ausgabe-Koordinatensystem auf denselben Wert wie die Eingabe-Feature-Class festzulegen.