Bei der Analyse von räumlichen Daten ist der Maßstab der Analyse häufig einer der wichtigsten Aspekte. Für zahlreiche Dichtewerkzeuge müssen Sie einen Wert für den Radius angeben. Die ausgewählte Entfernung sollte zum Maßstab der Frage in Beziehung stehen, die Sie beantworten möchten, oder zum Maßstab der ins Auge gefassten Korrekturmaßnahmen. Angenommen, Sie möchten mehr über Adipositas bei Kindern erfahren. Wie sieht Ihr Analysemaßstab aus? Bezieht er sich auf die einzelnen Haushalte oder auf einen Umkreis? Wenn dies der Fall ist, ist die Entfernung zum Definieren des Analysemaßstab eher gering und umfasst nur die Haushalte in einem oder zwei Häuserblocks. Oder wie sieht der Maßstab für die Korrekturmaßnahmen aus? Eventuell möchten Sie herausfinden, wo Kindern mehr Sportangebote in ihrer Freizeit gemacht werden sollen, um so der zunehmenden Adipositas bei Kindern entgegenzuwirken. In diesem Fall bezieht sich die Entfernung eher auf Schulbezirke. In einigen Fällen ist es nicht weiter schwierig, einen angemessenen Analysemaßstab zu ermitteln. Wenn Sie zum Beispiel Pendelmuster untersuchen und wissen, dass die durchschnittliche Fahrt zur Arbeit beispielsweise 20 Kilometer beträgt, sind 20 Kilometer eine angemessene Entfernung für die Analyse. In anderen Fällen ist es schwieriger, die Verwendung einer bestimmten Entfernung für die Analyse zu begründen. In diesen Fällen ist das Werkzeug Inkrementelle räumliche Autokorrelation am nützlichsten.
Immer dann, wenn Sie eine räumliche Cluster-Bildung in der Landschaft sehen, sehen Sie einen Beweis für die zugrunde liegenden räumlichen Prozesse, die im Gange sind. Kenntnisse über den räumlichen Maßstab dieser zugrunde liegenden Prozesse können Sie dabei unterstützen, eine angemessene Analyseentfernung auszuwählen. Das Werkzeug Inkrementelle räumliche Autokorrelation führt das Werkzeug Räumliche Autokorrelation (Morans I) für eine Reihe von ansteigenden Entfernungen aus, wobei die Intensität der räumlichen Cluster-Bildung für jede Entfernung gemessen wird. Die Intensität der Cluster-Bildung wird durch den zurückgegebenen Z-Wert bestimmt. In der Regel erhöht sich bei der Erhöhung der Entfernung auch der Z-Wert, was auf eine Intensivierung der Cluster-Bildung hinweist. An einer bestimmten Entfernung erreicht der Z-Wert in der Regel den Spitzenwert. Manchmal sind auch mehrere Spitzenwerte möglich.
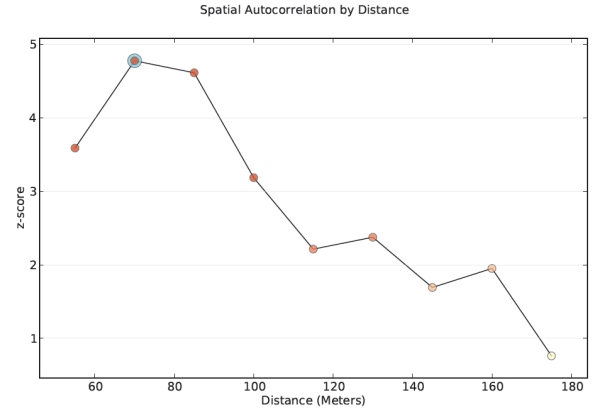
Spitzenwerte stellen Entfernungen dar, bei der die räumlichen Prozesse, die eine Cluster-Bildung fördern, am stärksten sind. Die Farbe jedes Punktes im Diagramm entspricht der statistischen Signifikanz der Z-Werte.
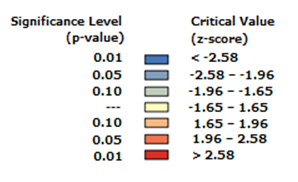
Eine Strategie zum Ermitteln eines angemessenen Analysemaßstabs besteht darin, die mit dem statistisch signifikanten Spitzenwert, der dem Maßstab der Fragestellung am besten wiedergibt, verknüpfte Entfernung auszuwählen. Häufig ist dies der statistisch signifikante Spitzenwert.
Wie werden die Werte für Anfangsentfernung und Entfernungsschrittgröße ausgewählt?
Alle Entfernungsmesswerte basieren auf Feature-Schwerpunkten, und die standardmäßige Anfangsentfernung ist die kürzeste Entfernung, mit der sichergestellt wird, dass jedes Feature über mindestens ein benachbartes Feature verfügt. In der Regel ist dies eine gute Wahl, es sei denn, das Dataset enthält Positionsausreißer. Ermitteln Sie, ob Positionsausreißer vorhanden sind, wählen Sie dann alle Features außer den Ausreißer-Features aus. Führen Sie anschließend die inkrementelle räumliche Autokorrelation nur für die ausgewählten Features aus. Wenn Sie für den Auswahlsatz eine Spitzenentfernung ermitteln, verwenden Sie diese Entfernung, um eine Matrixdatei für räumliche Gewichtung basierend auf allen Features (auch Ausreißern) zu erstellen. Wenn Sie mit dem Werkzeug Räumliche Gewichtungsmatrix erstellen eine Datei mit einer räumlichen Gewichtungsmatrix erstellen, legen Sie für den Parameter Anzahl der Nachbarn einen Wert fest, mit dem alle Features über mindestens diese Anzahl von benachbarten Features verfügt.
Der standardmäßige Wert für Inkrementelle Entfernung ist die durchschnittliche Entfernung zum nächsten benachbarten Feature der einzelnen Features. Wenn Sie anhand der oben genannten Strategien eine geeignete Startentfernung ausgewählt haben und weiterhin keine Spitzenentfernung angezeigt wird, versuchen Sie es mit kleineren oder größeren Entfernungsschrittgrößen.
Was ist, wenn nie Spitzenwerte im Diagramm angezeigt werden?
Bei der Verwendung des Werkzeugs Inkrementelle räumliche Autokorrelation kann es manchmal vorkommen, dass Sie ein Diagramm mit einem Z-Wert erhalten, die sich mit zunehmender Entfernung stetig weiter erhöhen, jedoch keinen Spitzenwert aufweisen. Dies geschieht meistens dann, wenn Daten aggregiert wurden und der Maßstab der Prozesse, die sich auf die Variable im Eingabefeld auswirken, kleiner als das Aggregationsschema ist. Versuchen Sie es mit einer geringeren Entfernungsschrittgröße, die möglicherweise subtilere Spitzenwerte eher erfasst. In einigen Fällen erhalten Sie jedoch keine Spitzenwert, da mehrere räumliche Prozesse im Untersuchungsgebiet vorhanden sind, die jeweils mit einer anderen Entfernung arbeiten. Dies ist häufig der Fall bei umfangreichen, verrauschten Punkt-Datasets (kein klares räumliches Muster der zu analysierenden Punktdatenwerte). In diesem Fall müssen Sie Ihren Analysemaßstab anhand anderer Kriterien begründen.
Interpretieren von Ergebnissen
In der Regel ermitteln Sie Spitzenentfernungen jedoch, indem Sie sich das Diagramm in der optionalen Datei mit dem Ausgabebericht ansehen. Der Bericht hat drei Seiten. Ein Beispiel für die erste Seite des Berichts ist nachfolgend dargestellt. Beachten Sie, dass dieses Diagramm drei Spitzenwerte für den Z-Wert in Bezug auf die Entfernungen von 5.000, 9.000 und 13.000 Fuß aufweist. Die erste Spitzenentfernung und die maximale Spitzenentfernung wird durch einen Halo hervorgehoben. Alle Spitzenwerte stellen Entfernungen dar, bei denen die räumlichen Prozesse, die eine Cluster-Bildung fördern, am stärksten sind. Sie können den Spitzenwert auswählen, der den Maßstab Ihrer analytischen Fragestellung am besten wiedergibt. In einigen Fällen wird nur ein Halo angezeigt, da sich der erste und der maximale Spitzenwert in derselben Entfernung befinden. Wenn keiner der Spitzenwerte des Z-Wertes statistisch relevant ist, wird keiner der Spitzenwerte durch einen hellblauen Halo hervorgehoben. Beachten Sie, dass die Farbe des geplotteten Z-Wertes mit der Legende der kritischen Werte für die statistische Signifikanz übereinstimmt.
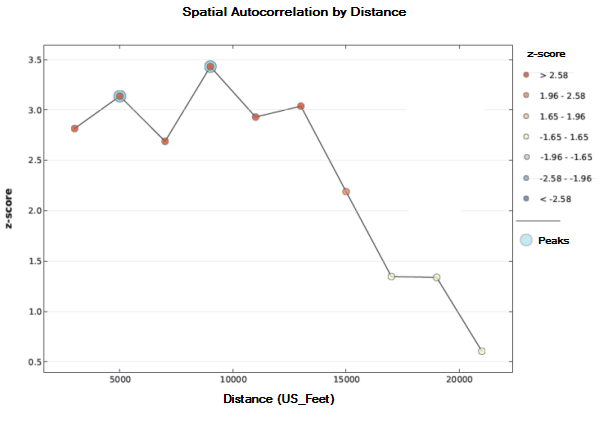
Auf der zweiten Seite des Berichts werden die Entfernungen und Z-Werte in einer Tabelle aufgeführt. Auf der letzten Seite des Berichts werden die verwendeten Parametereinstellungen und die Ausführungszeit des Werkzeugs dokumentiert. Um eine Berichtsdatei zu erstellen, geben Sie eine Pfad für den Parameter Ausgabebericht an.
Zusätzliche Ressourcen
- Videos mit Empfehlungen zur Ausführung einer Hot-Spot-Analyse:
- Im Lernprogramm zur Analyse räumlicher Muster werden Sie durch eine Analyse von Daten zum Dengue-Fieber unter Verwendung des Werkzeugs Inkrementelle räumliche Autokorrelation geführt.
- Siehe Auswählen eines Wertes für ein festes Entfernungsband unter Modellierung von räumlichen Beziehungen.
- Funktionsweise der Hot-Spot-Analyse umfasst eine Erläuterung zum Ermitteln eines geeigneten Analysemaßstabs.
- Eine aktuelle Liste aller verfügbaren Ressourcen für die räumliche Statistik finden Sie unter https://esriurl.com/spatialstats.