Lineare Regression ist eine Methode für überwachtes maschinelles Lernen, die vom Werkzeug Mit AutoML trainieren verwendet wird und die lineare Gleichung sucht, die die Korrelation zwischen der erklärenden Variablen und der abhängigen Variablen am besten beschreibt. Dazu wird eine Linie mithilfe der wenigstmöglichen Quadrate an die Daten angepasst. Dabei wird versucht, die Summe der Residuenquadrate zu minimieren. Das Residuum entspricht der Entfernung zwischen der Linie und dem tatsächlichen Wert der erklärenden Variablen. Die Suche nach der am besten passenden Linie ist ein iterativer Prozess.
Im folgenden Beispiel wird eine sich ergebende Gleichung einer linearen Regression gezeigt:
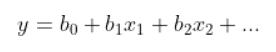
Im oben gezeigten Beispiel ist y die abhängige Variable, und x1, x2 usw. sind die erklärenden Variablen. Die Koeffizienten (b1, b2 usw.) erklären die Korrelation zwischen den erklärenden Variablen und der abhängigen Variablen. Das Zeichen (+/-) der Koeffizienten gibt an, ob die Variable positiv oder negativ korreliert. b0 ist der Schnittpunkt, der den Wert der abhängigen Variablen angibt, wobei angenommen wird, dass alle erklärenden Variablen 0 entsprechen.
In der folgenden Abbildung wird ein lineares Regressionsmodell mit der Regressionslinie y = 153,21 + 900,39x beschrieben. Das Modell beschreibt die Beziehung zwischen der abhängigen Variablen (Diabetes-Vorstufen) und der erklärenden Variablen (Triglyceridspiegel im Serum). Es wird eine positive Korrelation gezeigt. In diesem Beispiel wird ein lineares Regressionsmodell mit zwei Variablen veranschaulicht. Obwohl es nicht möglich ist, Modelle mit mehr als drei Variablen zu visualisieren, kann ein Modell praktisch beliebig viele Variablen enthalten.
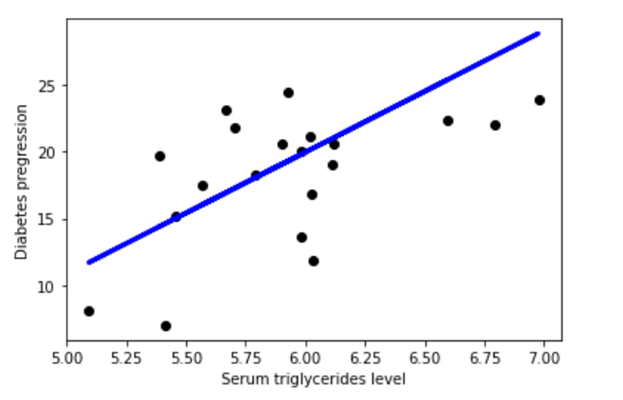
Ein lineares Regressionsmodell erleichtert das Vorhersagen des Wertes einer abhängigen Variablen und kann auch dabei helfen, die Genauigkeit der Vorhersage zu erklären. Dies wird mit den R-Squared- und p-Werten angegeben. Der R-Squared-Wert gibt an, wie viel der Variation in der abhängigen Variablen durch die erklärende Variable erklärt werden kann. Der p-Wert erklärt, wie zuverlässig diese Erklärung ist. Die R-Squared-Werte liegen zwischen 0 und 1. Ein Wert von 0,8 bedeutet, dass die erklärende Variable 80 Prozent der Variation der beobachteten Werte der abhängigen Variablen erklären kann. Ein Wert von 1 bedeutet, dass eine perfekte Vorhersage möglich ist, was in der Praxis selten ist. Ein Wert von 0 bedeutet, dass die erklärende Variable überhaupt nicht zur Vorhersage der abhängigen Variablen beiträgt. Mit einem p-Wert können Sie testen, ob die Auswirkung der erklärenden Variablen auf die abhängige Variable signifikant von 0 abweicht.