因果推断分析的工作原理—ArcGIS AllSource

因果推断分析工具通过平衡混杂变量来估计连续暴露变量和连续结果变量之间的因果效应。该工具将使用倾向得分匹配或者逆倾向得分加权为每个观测值分配权重，以使混杂变量与暴露变量变得不相关，从而隔离暴露和结果之间的因果效应。结果为暴露响应函数 (ERF)，用于估计结果变量如何响应暴露变量的变化。例如，可以估算不同施肥量（暴露）下玉米产量（结果）的平均增幅，并剔除影响玉米产量的土壤类型、耕作技术和环境变量等混杂变量。 ERF 将显示为图形图层并显示在地理处理消息中。此外，可以估计单个观测的因果效应并创建基于目标的目标。例如，可以估计每个农场每年生产给定数量的玉米所需的施肥量。

因果推断分析背景

因果推断分析是一个统计领域，用于对两个感兴趣变量之间的因果关系进行建模。一个变量（称为暴露或治疗变量）将直接更改或影响另一个变量（称为结果变量）。相关性通常用来衡量一个变量的变化如何与另一个变量的变化相关联；但是，相关性并不一定意味着一个变量将导致另一个变量。它们可能都会受到其他因素的影响。例如，冰淇淋销量与防晒霜销量之间可能存在较强的正相关关系。但是，您无法得出结论：冰淇淋销量增加将导致防晒霜销量增加。在得出因果结论之前，必须考虑其他因素，例如温度、紫外线指数或一年中的月份。同时影响暴露变量和结果变量的因素称为混杂变量，必须将其包含在内并加以考虑，以精确捕获暴露变量和结果变量之间的因果关系。

因果分析将从基于研究或常识的假设开始。例如，考虑运动对健康的影响。有证据和常识表明，定期锻炼可以改善健康，但这些变量还取决于许多其他混杂变量，例如饮食习惯、生活方式选择以及进入安全锻炼场所的机会。在这种情况下，在考虑了各种重要的混杂变量后，可以使用因果推断分析来隔离暴露变量（例如，每天锻炼的时间）对结果变量（例如，健康结果）的影响。

在设计的实验中，可以使用随机对照试验 (RCT) 来控制混杂变量。随机对照试验广泛应用于临床研究，其中参与者被随机分配不同的暴露水平，并对他们的结果进行比较。例如，一个人每天锻炼 10 分钟，另一个人锻炼一小时，还有一个人根本不锻炼。由于他们的暴露变量是随机分配的，因此组内健康结果的任何差异都不能归因于暴露变量以外的任何因素。

然而，在现实世界中，创建对照实验组通常是不可能或者不道德的。例如，要研究污染对抑郁症的影响，您无法从道德上将人们暴露在高污染环境中以观察其抑郁症会发生什么。相反，您只能观察人们已经历的污染程度并观察其抑郁率。然后，可以使用因果推断分析，通过模仿对照实验设计，根据观测数据对因果关系进行建模。通过估计每个观测的倾向得分来实现这一点，并且倾向得分用于估计观测的一组平衡权重。通过对平衡权重进行配置，其将保留暴露变量和结果变量之间的因果关系，但会移除混杂变量对暴露变量的影响，从而对因果关系进行无偏差估计。生成的加权观测与通过 RCT 采集的数据集具有类似属性，可以通过多种方式从中进行推断，这些方式与通过设计的实验采集的数据集相同。

用于估计平衡权重的两种常见方法是倾向得分匹配和逆倾向得分加权。在倾向得分匹配中，将对每个观测与具有相似混杂变量（通过其倾向得分的相似性来衡量），但具有不同暴露值的各种其他观测进行匹配。通过将观测的结果值与其匹配的结果值进行比较，可以了解如果具有不同的暴露，则观测可能具有的结果值。分配给每个观测的平衡权重是其与任何其他观测相匹配的次数。在逆倾向得分加权中，将通过反转倾向得分并乘以暴露的总体概率来分配平衡权重。此过程增加了不常见观测（低倾向得分观测）的代表性，并减少了常见观测（高倾向得分）的代表性，以使混杂变量的影响在暴露变量的所有值中保持成比例。

倾向得分匹配或逆倾向得分加权的平衡权重并非始终充分平衡混杂变量，因此需要对阈值进行比较来计算其加权相关性。如果相关性低于阈值（意味着相关性较低），则确定其经过平衡，并且需要估计 ERF。然而，如果平衡权重未充分平衡混杂变量，则该工具将返回错误并且不会生成 ERF。

示例应用

以下是该工具的示例应用：

调查美国青少年接触烟草产品广告对烟草使用的影响。在本示例中，暴露变量是每个青少年接触广告的量，结果变量是每个青少年在给定时间段内消耗的烟草量。混杂变量应该是已知或怀疑与青少年接触或使用烟草制品有关的任何其他变量，例如社会经济变量、家人或朋友直接接触烟草制品、烟草制品的价格以及烟草制品的可获得性。可以选择许多暴露变量以调查青少年烟草使用（例如直接接触家庭成员的烟草产品），但烟草产品广告是一个非常有用的暴露变量，因为如果发现其导致青少年烟草使用大幅增加，那么可以通过监管来减少广告。但是，减少成年家庭成员的烟草产品使用将更加困难。
估计精准农业中施肥量对玉米产量的因果影响，同时控制每块农田的土壤类型、耕作技术、环境变量和其他混杂变量。例如，如果每个农场增加 10% 的施肥量，则将额外产生多少玉米？
估计血压与心脏病发作风险之间的因果关系，从而控制诸如年龄、体重、社会人口统计学变量以及获取医疗保健等混杂变量。
在空间数据中，与其他要素的距离通常是非常有用的暴露变量。例如，与杂货店、绿地和医院的距离将导致其他变量的变化：距离杂货店越远，获取食物的机会则越少；距离医院越远，则获取医疗保健的机会则越少，以此类推。出于类似的原因，即使暴露变量和结果变量不是空间变量，空间变量以及与其他要素的距离也常常是重要的混杂变量。

但是，因果推断分析具有许多限制和假设，必须满足这些限制和假设，才能使因果效应的估计公正且有效。以下是因果推断分析的一些假设和限制：

必须包含所有重要的混杂变量。这是因果推断分析的一个强有力的假设，这意味着如果未将与暴露变量和结果变量相关的任何变量纳入混杂变量，则因果效应的估计将会存在偏差（因果效应和任何缺失混杂变量的混杂效应的混合）。该工具无法确定是否已包含所有重要混杂变量，因此考虑将包含的混杂变量至关重要。如果存在不可用的重要混杂变量，请极其谨慎地解释结果或者请勿使用该工具。
必须移除混杂变量和暴露变量之间的相关性，以隔离因果效应。在因果推断分析中，移除混杂变量和暴露变量之间的相关性称为平衡，该工具将使用各种平衡过程。但是，它无法始终充分地移除混杂变量和暴露变量之间的相关性。如果平衡过程未充分平衡混杂变量，则该工具将返回错误并且不会估计 ERF。有关错误以及解决方法的详细信息，请参阅实现混杂变量平衡的提示。
ERF 无法推断出用于估计的暴露值范围之外。例如，如果暴露变量为年平均温度，则无法估计高于样本中温度的相应温度的新结果。例如，这意味着您可能无法预测未来平均温度将超过任何当前平均温度时的结果。此外，默认情况下，该工具将修剪（从分析中移除）最高和最低 1% 的暴露值，因此 ERF 的范围甚至比样本中观测的暴露值更窄。

工具输出

该工具将创建各种输出，可用于调查暴露和结果变量之间的因果关系。结果将以图形图层、地理处理消息、输出要素（或表）以及输出 ERF 表的形式返回。

暴露响应函数

该工具的主要结果为 ERF，用于估计结果变量如何响应暴露变量的变化。如果所有总体成员均更改为具有相同的暴露变量，但保留所有现有混杂变量，则 ERF 将估计结果变量的新总体平均值（所有总体成员的平均值）。例如，对于美国所有县，如果暴露变量为 PM2.5，结果变量为哮喘住院率，则 ERF 将估计如果全国 PM2.5 水平增大或减小，同时保持所有其他变量（例如社会人口统计变量）与 PM2.5 变化之前相同，全国平均哮喘住院率将如何变化。

在活动地图中运行时，图形图层将添加至显示 ERF 的地图中。相同的 ERF 图像也会显示在消息中。

暴露响应函数 — 如果所有总体成员均更改为具有相同的暴露值（x 轴），则 ERF 将估计结果变量的平均值（y 轴）。

粉色曲线为暴露（x 轴）和结果（y 轴）变量之间的 ERF。观测将在散点图背景中显示为浅蓝色气泡，较大的气泡指示该要素具有较大的平衡权重，对 ERF 估计的贡献较大。对于倾向得分匹配，如果观测没有任何匹配，则会将其绘制为浅灰色的点。图表中未显示修剪后的观测。

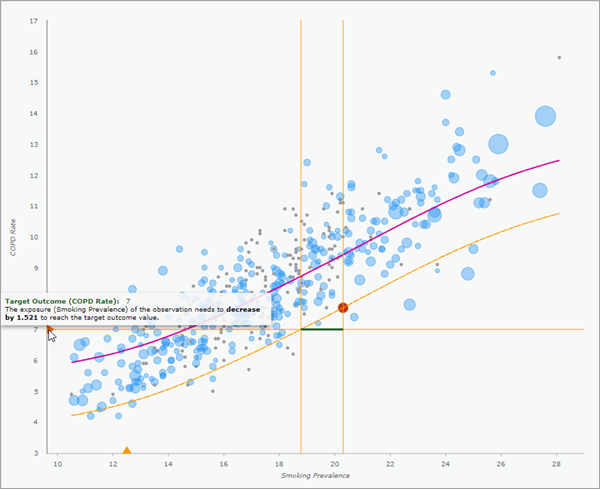
ERF 还包含一条蓝色水平线，显示了结果变量的平均值，以便将其与不同暴露变量水平的估计平均值进行比较。例如，在上图中，如果所有县将其吸烟率更改为低于大约 17.5（平均线穿过 ERF）的相同值，则总体 COPD 率将从当前水平下降。同样，如果所有国家的吸烟率都高于 17.5，则慢性阻塞性肺病的总体发病率将会增加。

您还可以使用输出暴露响应函数表参数来创建 ERF 表。创建后，该表将包含最小和最大暴露之间 200 个均匀间隔的暴露值以及相应的响应（结果）值。如果提供任何目标暴露或目标结果值，则其也将与估计的暴露或响应值一起追加到表的末尾。

混杂变量平衡统计数据

消息的平衡结果部分将显示每个混杂变量与暴露变量之间的原始相关性和加权绝对相关性。由此可以看到平衡权重是否有效地降低了混杂变量和暴露变量之间的原始相关性。如果权重在平衡方面有效，则加权相关性应低于原始相关性。消息表中的最后一行将显示平均值、中位数或最大绝对相关性，具体取决于平衡类型参数的值。

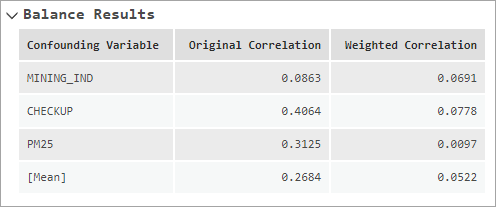
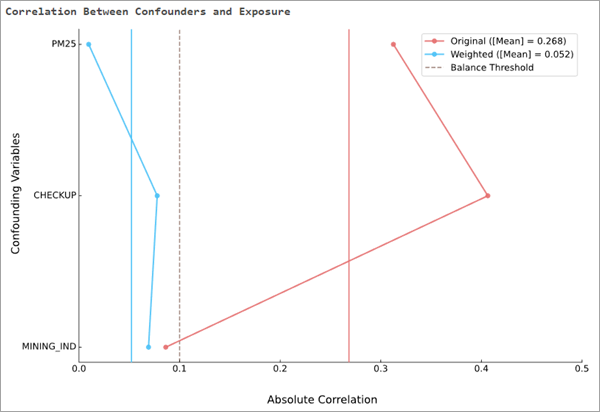
“混杂因素与暴露之间的相关性”消息图表将显示与表格相同的信息，但垂直折线图除外。对于每个混杂变量，原始相关性由红线连接，加权相关性由蓝线连接。原始和加权聚合相关性也将分别绘制为垂直的红色和蓝色条柱。如果权重可有效平衡混杂变量，则蓝线通常应位于红线的左侧。平衡阈值将绘制为垂直虚线，以便查看相关性与阈值的接近程度。例如，在下图中，两个混杂变量一开始具有相对较高的相关性（分别高于 0.3 和 0.4），但平衡权重已将相关性降低到小于 0.1。第三个混杂变量一开始具有较低的相关性（略低于 0.1），但平衡权重仍少量降低了相关性。总体而言，平均相关性从接近 0.27 降至 0.05 以下。

有关混杂变量平衡的详细信息，请参阅以下检查平衡混杂变量部分。

参数调整结果

这些消息还包含总结用于估计 ERF 的各种调整参数的部分。根据在该工具中指定的参数，可能会显示以下部分：

修剪结果 - 将显示原始观测数量（移除任何具有空值的记录后）、通过暴露修剪移除的观测数量、通过倾向得分修剪移除的观测数量以及修剪后剩余的最终观测数量。
匹配格网搜索结果 - 对于倾向得分匹配，将显示匹配参数搜索的结果。该工具将使用暴露立方图格的数量和暴露倾向得分的相对权重（比例）的各种组合，并显示每个组合的结果加权相关性。将以粗体突出显示导致最低加权相关性（最佳平衡）的组合。
变换平衡结果 - 对于回归倾向得分模型，将显示用于尝试找到平衡的混杂变量变换以及每个变换组合的加权相关性。将以粗体突出显示导致最低加权相关性的变换组合。
梯度提升平衡结果 - 对于梯度提升倾向得分模型，将显示梯度提升格网搜索的结果。该工具将尝试树数和学习率的九种组合，并显示每个组合的加权相关性。将以粗体突出显示导致最低加权相关性的组合。
产生最佳平衡的参数 - 对于倾向得分匹配，将显示导致最佳混杂变量平衡的暴露立方图格数量以及倾向得分与暴露的相对权重（比例）。对于梯度提升，将显示导致最佳平衡的树数、学习率和随机数生成器种子值。
平衡结果 - 将显示每个混杂变量的原始相关性和加权相关性，以及平均相关性、中值相关性或最大相关性。如果使用了变换，则还将显示每个混杂变量的变换。

有关确定消息中值的数量的详细信息，请参阅以下估计最佳平衡参数部分。

输出要素

输出要素或表将包含暴露、结果和混杂变量的副本，以及倾向得分、平衡权重（匹配计数或逆倾向得分权重）以及一个指示是否已修剪记录的字段。添加至地图时，将根据平衡权重绘制输出要素。由此可查看权重是否存在任何空间模式，这可能指示结果中某些区域的代表性过高或过低。

如果提供任何目标暴露或结果值，则每个提供的值都将在输出上创建两个附加字段。对于目标暴露值，第 1 个字段将包含观测收到目标暴露时的估计结果值，第 2 个字段将包含结果变量中的估计变化。正值指示结果变量将增大，负值指示结果变量将减小。对于目标结果值，第 1 个字段将包含会导致目标结果的暴露值，第 2 个字段将包含产生目标结果所需的暴露变量的变化。

如果您创建局部 ERF 弹出图表，则每个输出记录将在弹出窗格中显示局部 ERF。任何目标结果或暴露值将在 x 轴和 y 轴上显示为橙色三角形。可以单击三角形以打开和关闭水平或垂直条柱，以查看该值与局部 ERF 的交叉点。此外，可以将鼠标悬停在三角形上，以查看有关达到目标所需暴露或结果中变化的信息。有关详细信息，请参阅估计局部因果效应。

如果为 ERF 创建引导置信区间，则将创建两个附加字段，其中包含在引导样本中选择观测的次数以及观测包含在达到平衡的引导样本中的次数。建议您在这两个字段中查找空间模式。如果某些区域包含的平衡引导样本比其他区域更多，则置信区间可能存在偏差（通常会导致置信区间过窄）。有关详细信息，请参阅引导置信区间。

倾向得分

因果推断分析的一个基本组成部分为倾向得分。倾向得分定义为在给定混杂变量值的情况下，观测使用其观测到的暴露值的可能性（或概率）。较高的倾向得分意味着观测的暴露值对于具有相似混杂变量的个体来说是常见的，而较低的倾向得分意味着观测的暴露值对于具有相似混杂变量的个体来说是不常见的。例如，如果某人患有高血压（暴露变量），但没有高血压的任何风险因素（混杂变量），则其倾向得分可能较低，因为在没有任何风险因素的情况下患高血压相对罕见。相反，对于具有许多风险因素的人来说，高血压的倾向得分会更高，因为这种情况更加常见。

因果推断分析的两种方法将使用倾向得分：倾向得分匹配和逆倾向得分加权。每种方法都会为每个观测分配一组平衡权重，然后将这些平衡权重用于平衡混杂变量（有关详细信息，请参阅以下检查平衡混杂变量部分）。

倾向得分匹配

倾向得分匹配尝试通过将每个观测与具有相似混杂变量，但具有不同暴露值的各种观测进行匹配来平衡混杂变量。通过将观测的结果值与匹配观测的结果进行比较，可以了解如果具有不同的暴露（但保留相同的混杂变量），则观测可能具有的结果。找到所有观测的匹配后，分配给每个观测的平衡权重为该观测与任何其他观测相匹配的次数。例如，如果一个观测与任何其他观测都不匹配，则平衡权重将为零；如果该观测与所有其他观测相匹配，则平衡权重将等于观测的数量。

连续暴露变量的倾向得分匹配相对复杂，将在以下参考文献部分的第 4 项和第 5 项中提供完整的描述和推导。以下简单总结匹配过程：

该过程首先使用暴露立方图格的数量参数的值，根据暴露变量（类似于直方图的条柱）将观测划分为等间距的立方图格。通过将立方图格中观测的倾向得分与每个其他观测的反事实倾向得分进行比较，在每个立方图格内执行倾向得分匹配。反事实倾向得分是指如果观测具有相同的混杂变量，但具有不同的暴露（在本例中为每个暴露立方图格的中心值），则观测将具有的倾向得分。通过在暴露立方图格中查找倾向得分最接近其他每个观测的反事实倾向得分的观测来确定每个立方图格内的匹配。但是，由于立方图格中观测的暴露值通常不会与立方图格中心对齐，因此将根据暴露值与暴露立方图格中心之间的差值来添加附加惩罚。惩罚量将由倾向得分与暴露的相对权重参数（参考文献中称为比例参数）的值决定，总体匹配为倾向得分中绝对差值的加权总和最低的观测（倾向得分减去反事实倾向得分）和暴露（原始暴露减去立方图格中心值）。

逆倾向得分加权

逆倾向得分加权通过反转倾向得分并乘以具有给定暴露的总体概率来为每个观测分配平衡权重。这种因果推断方法将为具有低倾向得分的观测提供较高的平衡权重，为具有高倾向得分的观测提供较低的平衡权重。这种加权方案背后的原因是，倾向得分是衡量特定混杂变量集的暴露值常见或不常见程度的指标。通过提高不常见观测（倾向得分较低的观测）的影响（增大平衡权重）并降低常见观测的影响，混杂变量的总体分布将在暴露变量的所有值中保持成比例。

注：

核密度估计 (KDE) 用于估计暴露值的总体概率。 KDE 使用具有 Silverman 带宽的高斯内核，实现方式与 SciPy scipy.stats.gaussian_kde 包的 Python 函数一样。

倾向得分估计

倾向得分计算方法参数用于指定估计倾向得分的方式。每种方法都会构建一个模型，该模型使用混杂变量作为解释变量，使用暴露变量作为因变量。可以使用以下两种倾向得分计算方法：

回归 - 将使用普通最小二乘 (OLS) 回归来估计倾向得分。
了解有关 OLS 回归的详细信息
梯度提升 - 将使用梯度提升回归树来估计倾向得分。
了解有关梯度提升的详细信息

对于回归模型，通过假设正态分布标准化残差来为预测分配概率。梯度增强模型不会自然生成标准化残差，因此该工具构建第二个梯度增强模型来预测第一个模型残差的绝对值，从而提供标准误差的估计值。然后，对标准化残差使用 KDE（与以上逆倾向得分权重相同）以创建标准化残差分布。然后可以使用该分布来估计暴露和混杂变量值的所有组合的倾向得分。

在构建各自的模型之前，回归和梯度提升都会将所有变量重新调整到介于 0 到 1 之间。

检查平衡混杂变量

要使 ERF 成为因果效应的无偏差估计，必须包含并平衡所有混杂变量，这意味着混杂变量必须与暴露变量不相关。由于根据定义，混杂变量与暴露变量相关，因此将始终未对原始混杂变量进行平衡。但是，平衡权重（来自倾向得分匹配计数或逆倾向得分权重）的目的是对每个观测进行加权，从而平衡加权观测，但将保留暴露变量和结果变量之间的因果关系，由此允许对 ERF 进行无偏差估计。

要确定平衡权重是否有效平衡混杂变量，需要计算每个混杂变量和暴露变量之间的加权相关性。然后，聚合加权相关性的绝对值并与阈值进行比较。如果聚合相关性小于阈值，则确定混杂变量经过平衡。可以使用平衡类型参数指定聚合类型（平均值、中值或最大绝对相关性），并在平衡阈值参数中提供阈值。默认情况下，该工具将计算绝对平均相关性并使用阈值 0.1。

注：

对于连续混杂变量，可以使用加权 Spearman 排名相关系数来计算加权相关性。这种相关性与传统 Pearson 相关系数类似，但其使用变量的加权排名来代替原始值。使用排名可使相关性对于异常值和奇特形状的分布更加稳健。对于类别混杂变量，将使用加权 eta 统计数据来计算加权相关性，该统计数据使用暴露变量的加权排名。 eta 统计数据与类别变量的绝对 Pearson 相关性非常接近（两者都可以定义为 R 平方的平方根，即确定系数），并且使用加权排名代替原始暴露值使其接近等于加权 Spearman 相关性的绝对值。

实现混杂变量平衡的提示

如果平衡权重未充分平衡混杂变量，则该工具将返回错误并且不会生成 ERF；但是，仍将显示各种消息，其中包含有关每个混杂变量的加权相关性的信息。当您遇到此错误时，请查看消息以确定平衡权重对相关性的降低程度以及加权相关性与平衡阈值的接近程度。

当该工具无法实现平衡时，请考虑是否遗漏了任何相关的混杂变量，并将遗漏的任何变量包括在内。接下来，尝试倾向得分计算方法或平衡方法参数的不同选项。但是，对于某些数据集，可能没有达到平衡的组合。

一般来说，混杂变量的原始相关性越强，对其进行平衡将越困难。对于强相关的混杂变量，可能需要大量样本，才能实现足够的平衡。对于类别混杂变量，类别越多，则平衡将越困难。可能需要合并一些类别，特别是如果每个类别中暴露变量变化很小或观测数量较少（通常少于 5 个）。

但是，如果您可以接受在 ERF 中引入偏差，则可以通过提高平衡阈值或使用更宽松的平衡类型来实现平衡。

通常，平衡阈值越低，表明因果效应估计中偏差的容差越小；但阈值越小，则平衡将越困难。对于平衡类型，使用相关性平均值可确保混杂变量大体平衡，但是如果足够多的相关性较低的混杂变量使平均值低于阈值，则仍然允许一些混杂变量具有较大的相关性。最大值选项最保守，它要求每个混杂变量都低于阈值；但是，如果即使单个混杂变量略高于阈值，也会将混杂变量视为不平衡。中值选项最宽松，它允许最多一半的相关性非常大，并且仍被视为平衡。

估计最佳平衡参数

实现混杂变量平衡通常比较困难，因此该工具将尝试各种优化和搜索，以找到导致混杂变量尽可能平衡的调整参数。执行的优化取决于工具的各种参数，以下各部分将对此进行描述。

匹配参数搜索

在倾向得分匹配中，匹配结果取决于暴露立方图格的数量和倾向得分与暴露的相对权重参数的值，但是难以预测会产生最佳平衡的值。此外，其中一个值的微小变化可能会导致另一个值的较大变化，因此找到一对有效工作的值尤其困难。如果未提供参数值，则该工具将尝试各种组合，并在消息中以表格形式显示结果。在表格中，行为暴露立方图格的数量，列为相对权重（通常称为比例）。每个组合的加权相关性将显示在格网中，任何达到平衡的组合都会在值旁边显示一个星号。将以粗体突出显示导致最低加权相关性（最佳平衡）的组合。如下图所示，对于两个参数的不同值，加权相关性可能存在显著变化。

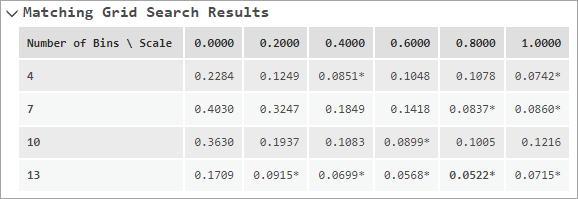
该工具将尝试的相对权重范围介于 0 到 1 乘以 0.2 之间，但测试的暴露立方图格数量取决于观测数量。测试值的范围介于观测数量的四次方根到三次方根的两倍之间。测试值将均匀递增，将测试的值不少于 3 个，不超过 10 个。

回归变换

当使用回归以计算倾向得分时，如果混杂变量不平衡，则将对任何连续混杂变量应用各种变换。如果在任何时候混杂变量达到平衡，则该过程将结束，并且当前的一组变换将用于构建 ERF。

该过程将从最不平衡的混杂变量（最大加权相关性）开始，并应用一系列变换。将保留实现最佳平衡的转换，并针对下一个混杂变量重复该过程。此过程将继续进行，直到使用所有变换对所有混杂变量进行了测试为止，如果混杂变量仍然不平衡，则该工具将返回错误并且不会生成 ERF。

将执行以下变换，其中会对进行变换的混杂变量的值进行一些限制：

自然对数 - 仅适用于具有正值的混杂变量
平方 - 仅适用于具有非负值的混杂变量
平方根 - 仅适用于具有非负值的混杂变量
立方体
立方根

实现最佳平衡的变换将显示在消息的平衡结果部分中，并且变换尝试的完整历史记录将显示在变换平衡结果部分中。

在倾向得分匹配中，来自原始（未变换）混杂变量的暴露立方图格数量和相对权重值将用于所有变换组合。由此通过针对每个变换组合重复匹配参数搜索来防止计算时间过长。平方变换仅限于非负值，以使混杂变量值的排序在变换前后不会改变，在重用暴露立方图格的数量和根据原始观测确定的相对权重时，这将非常重要。

梯度提升参数搜索

当使用梯度提升来计算倾向得分时，将会测试树的数量和学习率的各种组合。如果在任何时候混杂变量达到平衡，则该过程将结束并使用当前的树数量和学习率。该过程将尝试最多 9 种组合：树的数量等于 10、20 和 30 棵树，学习率等于 0.1、0.2 和 0.3。

实现最佳平衡的树数量和学习率将显示在消息的实现最佳平衡的参数部分中，并且参数组合的完整历史记录将显示在梯度提升平衡结果部分中。

与回归变换不同，对于树的数量和学习率的每个组合，将重复对暴露立方图格的数量和相对权重进行匹配参数搜索。由于这 4 个参数中任何一个参数的微小变化都可能导致其他参数的最佳值发生较大变化，因此将执行更加深入的搜索。

估计暴露响应函数

平衡过程将为每个观测分配平衡权重（匹配计数或逆倾向得分权重），这些权重是估计暴露响应函数的基础。每个加权观测（有时称为伪总体）都具有暴露值、结果值和权重，目标是为加权观测拟合一条平滑曲线 (ERF)。在估计 ERF 时，每个观测都会与其权重成比例地影响估计。换句话说，权重等于 3 的 1 个观测的贡献相当于权重等于 1 的 3 个观测。同样，任何权重为零的观测都不会对 ERF 产生影响，从而有效地过滤掉该观测。

对于暴露变量的给定值（x 轴），相关响应值（y 轴）将估计为观测结果值的加权移动平均（有时称为核平滑器）。加权平均值中的权重为平衡权重乘以以三个标准差修剪的高高斯核的权重。

当对暴露变量的所有值执行此过程时，结果为一条穿过观测，并被拉向具有最大权重的观测的平滑曲线。

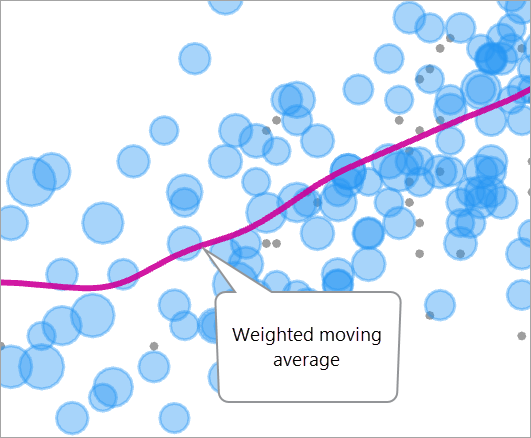
带宽估计

ERF 公式中的核取决于控制 ERF 曲线平滑度的带宽值（高斯核的标准差），指定相应的带宽对于生成真实且精确的 ERF 至关重要。对于同一组加权观测，较大的带宽值将导致更加平滑的 ERF。下图显示了用于同一观测的 3 个带宽值：

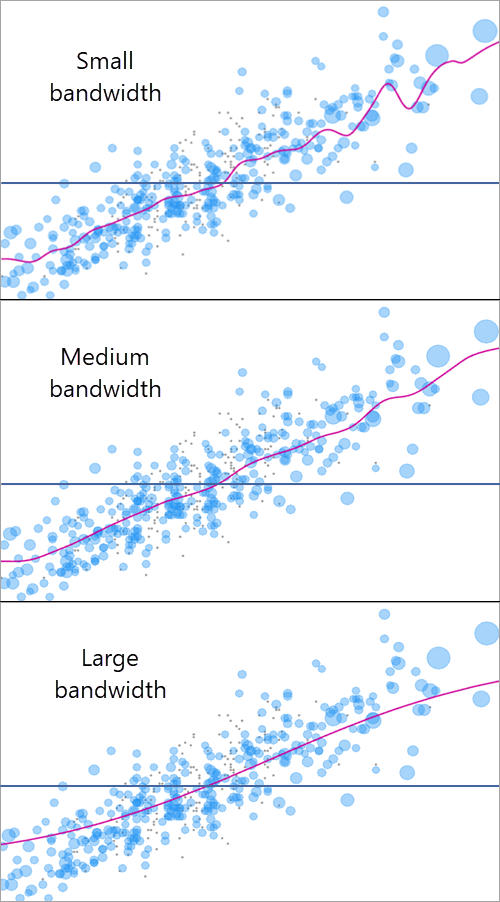
可以使用带宽估计方法参数以选择估计带宽值的方式。可以使用 3 种带宽估计方法：

插件 - 使用快速经验法则公式来估计带宽值。此选项为默认选项，计算速度较快，并且通常可生成精确且真实的 ERF。该方法是 Fan (1996) 方法的加权变体，将从拟合所有观测的加权四阶全局多项式的二阶导数得出带宽值。
交叉验证 - 将使用最小化均方交叉验证误差的带宽值。此选项的计算时间最长，但在统计理论中是最有根据的。但是，对于大型数据集，交叉验证倾向于估计过小的带宽值并产生过于弯曲的 ERF。
手动 - 将使用带宽参数中提供的自定义带宽值。当其他选项产生的带宽值导致 ERF 过于平滑或过于弯曲时，建议使用此选项。在这种情况下，请检查其他方法估计的带宽值，并进行任何必要的校正以调整平滑度。

估计的带宽值将打印在消息的底部。

注：

对于插件和交叉验证方法，如果估计的带宽值小于曝光值之间的最大差距，则将估计最大的差距。这样可以确保每个曝光值均具有足够的数据进行加权平均。要使用较小的带宽值，请提供手动带宽值。

估计局部因果效应

通过选中启用暴露响应弹出窗口参数，可以为输出要素或表中的每条记录创建局部 ERF。如果选中此参数，则输出将在每个输出要素或表记录的弹出窗口中包含 ERF 图表。弹出窗口将显示如何估计单个观测的结果变量以响应其暴露变量的变化。局部 ERF 的形状与全局 ERF 相同，但其会向上或向下移动以通过单个观测。此外，如果提供了任何目标结果或暴露值，则其将与实现目标所需的暴露或结果变化一起显示在弹出图表中。

创建局部 ERF 或者使用目标暴露或结果值需要对所有观测进行固定暴露效应的附加假设。这是一个强假设，违反该假设可能会导致存在偏差或误导性的结果。固定暴露效应假设意味着暴露对结果的影响在总体的所有个体中均恒定。换句话说，考虑到其起始暴露，增加固定量的暴露将会以相同的方式更改每个人的结果，不考虑任何其他变量（包括但不限于测量的混杂因素）的水平。例如，要将施肥量从每英亩 150 磅增加到每英亩 175 磅，需要将所有农场的玉米产量增加相同数量，不考虑其当前的玉米产量、土壤类型、耕作技术或其他混杂变量。

当不存在效应修饰因子（即影响结果如何对个体级别上的暴露作出响应的变量）时，此假设是合理的。然而，诸如性别、种族或教育水平等社会人口变量通常为效应修饰因子，并且其通常作为混杂变量包含在因果推断模型中。由此可以很好地平均所有修正变量级别上的效应修正，从而估计全局平均因果效应 (ERF)。但是，全局 ERF 并不代表由效应修饰因子级别定义的任何特定子组。例如，就业培训计划可能会显示，培训时间越长，则就业机会将越多。然而，在以黑人或西班牙裔为主的社区，在经过一定时间的培训后，就业机会将会趋于稳定，这可能暗示着系统性的招聘歧视。因此，全局 ERF 可能会无意中掩盖这些社区面临的差异。全局 ERF 代表暴露对总体平均结果的影响；但是，在存在效应修饰因子的情况下，在以黑人或西班牙裔为主的地区，全局 ERF 可能无法准确代表暴露对结果的影响。

当模型包含效应修饰因子时，局部 ERF 无效。处理效应修饰因子的一种方法是分层，涉及根据修正变量的值将观测划分为层（或子组）。通过按层分离效应修饰因子并为每个层构建独立的 ERF，可以分别检查每个组内暴露和结果之间的关系。由此可以了解暴露对结果的影响在不同级别的效应修饰因子中是否有所不同。

引导置信区间

可以使用创建引导置信区间参数为 ERF 创建 95% 的置信区间。创建后，置信区间将在输出图形图层和消息中的 ERF 上方和下方绘制为虚线。如果创建了输出 ERF 表，则其还将包含置信上限和下限的字段。

置信区间为 95% 的 ERF — 95% 的置信区间在 ERF 上方和下方显示为虚线。

对于任何给定的暴露变量值，置信区间是结果变量总体平均值的界限。由于总体平均值的变异性小于总体中各个成员的变异性，因此散点图的大多数点通常不会落在置信区间内，但这并不表示存在问题。出于类似的原因，置信区间仅适用于全局 ERF，而不能应用于任何局部 ERF。

置信区间是使用 M-out-of-N 引导创建的。此过程需要从 N 个观测中随机采样 M 个观测，其中 M=2*sqrt(N)，如 DasGupta (2008) 所建议的那样。然后，该工具将对随机引导样本执行整个算法（最佳参数搜索、倾向得分估计、平衡测试和 ERF 估计）。生成的 ERF 通常与原始 ERF 相似，但不会完全相同。通过多次重复此过程，您可以看到在获取不同的随机观测样本时 ERF 的变化程度。由此产生的 ERF 的变化推动了置信区间的创建。

如果引导样本未达到平衡（由平衡类型和平衡阈值确定），则将放弃引导样本。该工具将继续执行引导，直到 5*sqrt(N) 个引导样本达到平衡为止。导出该值是为了使每个观测平均包含在至少 10 个平衡引导样本中。由此可对整个暴露范围的上限和下限进行稳定的估计。在 25*sqrt(N) 次引导尝试后，如果仍然没有足够的平衡引导，则将不会创建置信区间，并且将返回警告消息。

虽然置信区间捕获了 ERF 的许多不确定性来源，但值得注意的是，要创建真正对应于因果效应上限和下限的置信区间，必须考虑所有潜在的不确定性来源。该工具中的引导过程结合了平衡过程和 ERF 估计的不确定性，但其无法解释其他可能的不确定性来源，例如变量值的不精确性或者 ERF 函数形式的选择（例如，加权移动平均，而非样条函数法或全局多项式）。此外，随着观测数量的增加，置信区间将变得任意狭窄，但这并不意味着 ERF 是因果效应的完美表征。

当创建引导置信区间时，输出要素或表将包含 2 个与引导相关的字段。第 1 个字段包含在引导样本中选择观测的次数，第 2 个字段包含在达到平衡并估计 ERF 的引导样本中包含观测的次数。即使没有足够的引导样本达到平衡以估计置信区间，也会创建这些字段。对于输出要素，第一列的值应显示少量空间模式（要素周边除外）。但是，如果第 2 个字段中存在空间模式，则可能指示未考虑的空间过程。例如，如果大多数平衡引导样本来自数据的特定区域，则这些区域在置信区间中的代表性过高，并且区间可能会不切实际地窄。如果您在平衡引导样本的计数中看到空间模式，请考虑包含空间混杂变量（例如地理区域）以解释缺失的空间效应。

对于输入表，每个引导将随机且均匀地选择 M 个观测。将通过替换执行采样，因此可以在同一引导中多次选择相同的观测。对于要素输入，将通过随机选择单个要素并将其及其 8 个最接近的相邻要素包含在样本中而生成引导样本。将重复此随机选择并进行替换，直到引导样本中至少包含 M 个观测为止。可以多次随机选择相同的要素，并且可以多次将其作为相邻要素包含在内。使用随机邻域（而非完全随机选择）将有助于校正未测量的空间混杂（尽管仍然鼓励您通过将空间变量作为混杂变量来校正空间混杂）。

由于 ERF 无法扩展到超出用于构建其的暴露值范围，因此将仅在随机样本中观测的最小和最大暴露之间创建每个引导样本的 ERF。这意味着最高和最低暴露值通常不在随机采样值的范围内，因此针对最极端的暴露值创建的引导 ERF 将较少。

所有引导完成后，通过假设每个暴露值的引导 ERF 值的 T 分布来创建 95% 置信区间。通过乘以 (M/N) 来重新调整 ERF 值的方差，以仅针对采样 M 值进行调整，自由度为可以为暴露值生成的引导 ERF 的数量减 1。此外，将使用与用于估计原始 ERF（与插件带宽相同的权重）相同的核平滑器来平滑置信区间的宽度。然后，将经过平滑的宽度与原始 ERF 相加或相减，以生成置信上限和下限。如果创建输出 ERF 表，则其将包含相应字段，这些字段具有经过平滑的标准差（平滑宽度除以临界值）以及可为暴露值生成的引导 ERF 数量。

参考资料

DasGupta, Anirban. 2008. "Asymptotic Theory of Statistics and Probability." 纽约州纽约市 Springer. ISBN 978-0-387-75971-5. https://doi.org/10.1007/978-0-387-75971-5.

Fan, Jianquin. 1996. "Local Polynomial Modeling and Its Applications: Monographs on Statistics and Applied Probability 66." (1st ed.). Routledge. https://doi.org/10.1201/9780203748725.

Imbens, Guido and Donald B. Rubin. 2015. "Causal Inference for Statistics, Social, and Biomedical Sciences: An Introduction." Cambridge: Cambridge University Press. https://doi.org/10.1017/CBO9781139025751.

Khoshnevis, Naeem, Xiao Wu, and Danielle Braun. 2023. "CausalGPS: Matching on Generalized Propensity Scores with Continuous Exposures." R package version 0.4.0. https://CRAN.R-project.org/package=CausalGPS.

Wu, Xiao, Fabrizia Mealli, Marianthi-Anna Kioumourtzoglou, Francesca Dominici, and Danielle Braun. 2022. "Matching on Generalized Propensity Scores with Continuous Exposures." Journal of the American Statistical Association. https://doi.org/10.1080/01621459.2022.2144737.

有关此主题的反馈?