趋势面法工具可通过全局多项式插值法将由数学函数(多项式)定义的平滑表面与输入采样点进行拟合。 趋势表面会逐渐变化,并捕捉数据中的粗尺度模式。
概念的背景
从概念上讲,趋势插值就像将一张纸放在凸起点(凸起到值的高度)之间。 下图展示了在平缓倾斜的山丘上的一组高程采样点。 这张纸是洋红色的。
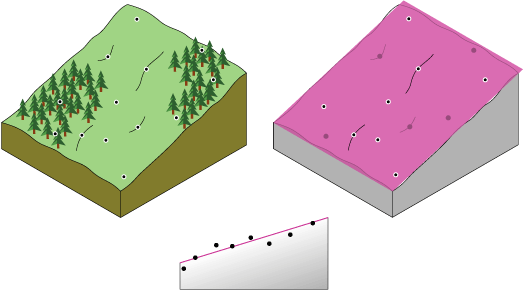
一张平面纸无法准确捕捉包含山谷的景观。 但是,如果将纸弯曲一次,就会更合适。 在数学公式中添加一项会产生类似的结果,即平面弯曲。 平面(纸上没有弯曲)是一阶多项式(线性)。 它允许一次弯曲是二阶多项式(二次),两次弯曲是三阶多项式(三次),依此类推。 此工具最多允许 12 次弯曲(十二阶)。 下图从概念上演示了拟合山谷的二阶多项式。
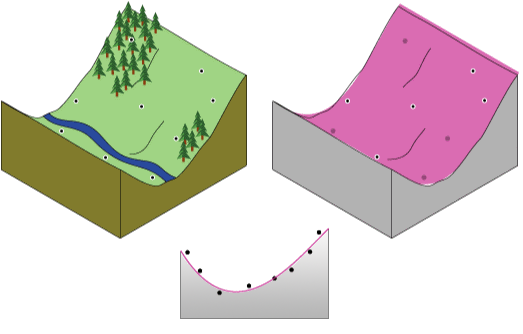
纸很少会通过实际测量点,从而使趋势插值成为不精确的插值器。 有些点在纸的上方,有些点在纸的下方。 但是,如果将每个点在纸上方的高度相加,并将每个点在纸下方的高度相加,则两个总和应该是相似的。 洋红色表面是通过使用最小二乘回归拟合获得的。 生成的表面最小化凸起值和纸张之间的平方差。
均方根 (RMS) 误差越低,插值表面越接近于输入点。 最常见的多项式阶数是一到三。 趋势表面插值用于创建平滑表面。
何时使用趋势插值法
趋势插值会生成一个平滑表面,表示感兴趣区域表面的渐变趋势。 此种插值法适用于以下几种情况:
- 当表面在感兴趣区域(例如,工业区的污染)上随区域逐渐变化时,将表面拟合到采样点。
- 检查或排除长期趋势或全局趋势的影响。 此类情况下,采用的方法通常为趋势面分析。
趋势插值使用描述物理过程(例如污染和风向)的低阶多项式创建逐渐变化的表面。 然而,多项式越复杂,就越难赋予其物理意义。 此外,计算出的表面极易受到异常值(极高和极低值)的影响,尤其是在边缘处。
趋势插值法的类型
趋势插值法共有两种基本类型,即线性和逻辑型。
线性趋势
线性趋势表面插值法用于创建浮点型栅格。 使用多项式回归,对输入点进行最小二乘曲面拟合。 此方法允许您控制用于拟合曲面的多项式的阶数。 要理解此方法,请考虑一阶多项式。 一阶线性趋势表面插值执行平面与输入点集的最小二乘法拟合。
趋势表面插值用于创建平滑表面。 生成的表面很少通过原始数据点,因为它对整个表面执行最佳拟合。 如果所用多项式阶数高于一阶,插值器所生成栅格的最大值和最小值可能会超过输入要素数据输入文件中的最小值和最大值。
逻辑型趋势
可生成趋势面的逻辑型选项适用于预测空间中给定的一组位置 (x,y) 处某种现象存在与否(以概率的形式)。 z 值为已分类随机变量,只有两种可能的结果,例如,濒危物种存在或该物种不存在。 这两个 z 值可以分别编码为 1 和 0。 此选项可根据值为零和一的各像元值创建连续的概率格网。
最大似然估计用于计算非线性概率曲面模型,而无需首先将模型转换为线性形式。
输出 RMS 文件
通过将输入数据集中位置的值与插值栅格表面中相同位置的值进行比较,RMS 误差文件包含插值的均方根误差。
RMS 误差值可用于确定用于插值 {order} 参数的最佳值,方法是更改阶数值,直到获得最低 RMS 误差。 还报告了卡方值。
示例
将多项式阶数设置为 3 时,运行趋势面法工具输出的 RMS 文件示例:
coef # coef
------ ----------------
0 -1192066.7888371
1 -1.78479492586755
2 -0.195982103615487
3 -8.87072249743903e-1
4 -2.0538267625596e-1
5 -3.85610088343239e-1
6 -1.46420255709888e-2
7 -5.31539027745154e-2
8 -2.59261094879031e-3
9 9.71651459136166e-4
------ ----------------
RMS Error = 296.957857221845
Chi-Square = 17019506.0103975对于此三阶趋势,通过对一系列方程产生的值求和,可以确定输出栅格中任何位置的预测值。 在该方程式中,x = 位置经度,y = 位置纬度,cn 项是上表中的系数值。 此三阶插值的方程式为:
Prediction(x,y) = c0 +
x·c1 + y·c2 +
x2·c3 + x·y·c4 + y2·c5 +
x3·c6 + x2·y·c7 + x·y2·c8 + y3·c9
实际上,系数 0 的项通常为截距。 在上述方程式中,先遍历一阶项,从 x 最大值开始直到没有 x 为止。 接着,遍历二阶项中 x 的值,然后按同样方法遍历三阶项。
注:
随着阶数的增加,这些方程遵循类似的模式。 例如,如果指定四阶,则将在 RMS 表中多指定五个值(系数 10、11、12、13 和 14),相应增加等数量的方程式来对其进行利用。