坡向的工作原理

需要 Spatial Analyst 许可。

需要 3D Analyst 许可。

坡向工具可确定下坡坡度所面对的方向。 输出栅格中各像元的值可指示出各像元位置处表面所朝向的罗盘方向。 将按照顺时针方向进行测量，角度范围介于 0（正北）到 360（仍是正北）之间，即完整的圆。 不具有下坡方向的平坦区域将赋值为 -1。

坡向

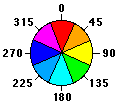
下图显示的是输入高程数据集和输出坡向栅格。

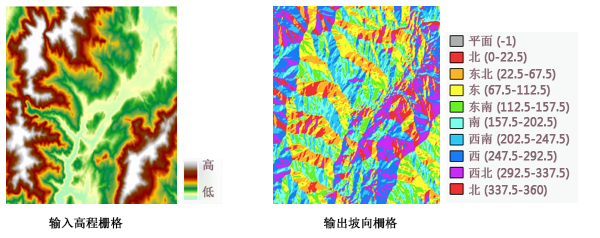
注：

表面参数工具可提供坡向的较新实施，建议使用该工具来代替坡向工具。 坡向工具可将一个平面与九个局部像元进行拟合，但是，平面可能并非景观的良好描述符，可能会掩盖或夸大感兴趣的自然变化。 表面参数工具可将一个表面与像元邻域而不是平面进行拟合，以提供针对地形的更自然的拟合效果。

坡向工具将使用 3 × 3 像元窗口来计算值，而表面参数工具允许窗口大小介于 3 × 3 到 15 × 15 像元之间。 较大的窗口尺寸对于高分辨率高程数据很有用，可以适当的比例捕获地表过程。 表面参数还可提供自适应窗口选项，该选项可评估地形的局部变异性，并为每个像元标识最大的适当邻域大小。 对于被河流、道路或陡坡中断的平缓且均匀的地形而言，该工具很有用。

如果您需要结果与先前工具运行结果完全匹配，或者快速执行时间比更好的算法更重要，则可以继续使用坡向工具的传统方法。

通过坡向工具，您可完成以下任务：

• 在寻找最适合滑雪的山坡的过程中，查找某座山所有朝北的坡。
• 在统计各地区生物多样性的研究中，计算某区域中各个位置的日照强度。
• 作为判断最先遭受洪流袭击的居住区位置研究的一部分，在某山区中查找所有朝南的山坡，从而判断出雪最先融化的位置。
• 识别出地势平坦的区域，以便从中挑选出可供飞机紧急着陆的一块区域。

计算方法和边缘效应

有两种方法可用于坡向计算。 可以使用方法参数在执行平面或测地线计算之间进行选择。

使用平面方法时，利用 2D 笛卡尔坐标系对投影平面执行计算。 使用测地线方法时，通过将地球形状视为椭球体，在 3D 笛卡尔坐标系中执行计算。

可以使用 3 像元 x 3 像元的邻域（移动窗口）来执行平面和测地线计算。 对于每个邻域，如果处理（中心）像元为 NoData，则输出也为 NoData。 计算还要求至少 7 个与处理像元相邻的像元具有有效值。 如果有效像元少于 7 个，则不执行计算，并且该处理像元处的输出将为 NoData。

输出栅格最外侧行列的像元为 NoData。 这是因为沿着输入数据集边界，这些像元没有足够的有效相邻像元。

平面方法

平面方法是用于计算坡向的传统方法。

平面坡向算法

移动的 3 x 3 窗口会访问输入栅格中的每个像元，对于位于窗口中心的每个像元，其坡向值将通过包含该像元 8 个相邻像元值的算法进行计算。 这些像元使用字母 a 至 i 进行标识，其中 e 表示当前正在计算坡向的像元。

表面分析窗口

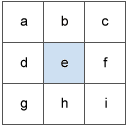
像元 e 在 x 方向上的变化率将通过以下算法进行计算：

[dz/dx] = ((c + 2f + i)*4/wght1 - (a + 2d + g)*4/wght2) / 8

• 其中：

  wght1 和 wght2 是有效像元的水平加权计数。

  例如：

  • 如果 c、f 和 i 均有一个有效值，则 wght1 = (1+2*1+1) = 4。
  • 如果 i 为 NoData，则 wght1 = (1+2*1+0) = 3。
  • 如果 f 为 NoData，则 wght1 = (1+2*0+1) = 2。

  除邻域位置为 a、d 和 g 以外，类似的逻辑也适用于 wght2。

像元 e 在 y 方向上的变化率使用以下算法进行计算：

[dz/dy] = ((g + 2h + i)*4/wght3 - (a + 2b + c)*4/wght4 ) / 8

• 其中：

  wght3 和 wght4 与 [dz/dx] 计算中的概念相同。

代入像元 e 在 x 方向和 y 方向上的变化率，坡向将通过以下算法进行计算：

aspect = 57.29578 * atan2 ([dz/dy], -[dz/dx])

然后，坡向值将根据以下规则转换为罗盘方向值（0 到 360 度）：

if aspect < 0 cell = 90.0 - aspect> else if aspect > 90.0 cell = 360.0 - aspect + 90.0 else cell = 90.0 - aspect

平面坡向计算示例

示例中，将计算移动窗口内中心像元的平面坡向值。

坡向示例输入

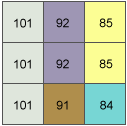
中心像元 e 在 x 方向上的变化率为：

[dz/dx] = ((c + 2f + i)*4/wght1 - (a + 2d + g)*4/wght2) / 8 = ((85 + 170 + 84)*4/(1+2+1) - (101 + 202 + 101)*4/(1+2+1)) / 8 = -8.125

像元 e 在 y 方向上的变化率为：

[dz/dy] = ((g + 2h + i)*4/wght3 - (a + 2b + c)*4/wght4) / 8 = ((101 + 182 + 84)*4/(1+2+1) - (101 + 184 + 85)*4/(1+2+1)) / 8 = -0.375

坡向计算如下：

aspect = 57.29578 * atan2 ([dz/dy], -[dz/dx]) = 57.29578 * atan2 (-0.375, 8.125) = -2.64

由于计算得出的值小于零，则根据最终规则得出：

cell = 90.0 - aspect = 90 - (-2.64) = 90 + 2.64 = 92.64

中心像元 e 的值 92.64 表明它的坡向为朝东。

平面坡向示例输出

测地线方法

测地线方法通过将地球形状视为椭球体，在 3D 地心坐标系（也称为地心地固 (ECEF) 坐标系）中测量表面坡向。 计算结果不受数据集投影方式的影响。 如果在空间参考中定义了 z 单位，此方法将使用输入栅格的 z 单位。 如果输入的空间参考未定义 z 单位，则需要使用 z 单位参数进行定义。 使用测地线方法生成的坡向比使用平面方法生成的更精确。

测地线坐标转换

ECEF 坐标系是以地心为原点的 3D 右手笛卡尔坐标系，其中所有位置均由 X、Y 和 Z 坐标表示。 有关以地心坐标系表示的目标位置 T 的示例，请参见下图。

将表面栅格从输入坐标系转换到 3D 地心坐标系中。

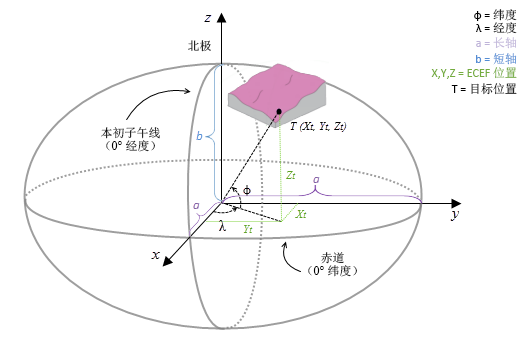
测地线计算使用基于其测地坐标（纬度 φ、经度 λ、高度 h）计算的 X, Y, Z 坐标。 如果输入表面栅格的坐标系为投影坐标系 (PCS)，则需要先将栅格重新投影到地理坐标系 (GCS)，其中每个位置均具有测地坐标，然后将其转换为 ECEF 坐标系。 高度 h（z 值）是以椭球体表面为参考的椭球体高度。 请参见下图。

椭球体高度

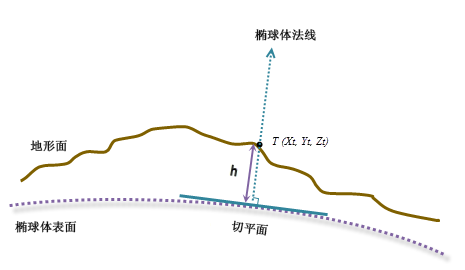
要从测地坐标（纬度 φ、经度 λ、高度 h）转换为 ECEF 坐标，请使用以下公式：

X = (N(φ)+h)cosφcosλ

Y = (N(φ)+h)cosφsinλ

Z = (b2/a2*N(φ)+h)sinφ

• 其中：
  • N( φ ) = a²/ √(a²cosφ²+b²sinφ²)
  • φ = 纬度
  • λ = 经度
  • h = 椭球体高度
  • a = 椭球体的长轴
  • b = 椭球体的短轴

在以上公式中，椭球体高度 h 以米为单位。 如果以任何其他单位指定输入栅格的 z 单位，则将其从内部转换为米。

坡向计算

某一位置的测地线坡向是在平行于椭球体表面的平面上相对于北向的下坡表面的方向。

要计算每个位置处的坡向，可以使用最小二乘法 (LSM) 在每个处理像元周围拟合 3 像元 x 3 像元的邻域平面。 LSM 中的最佳拟合可使实际 z 值与拟合 z 值之间的平方差 (dz_i) 的总和最小。 有关示例，请参见下图。

最小二乘拟合示例

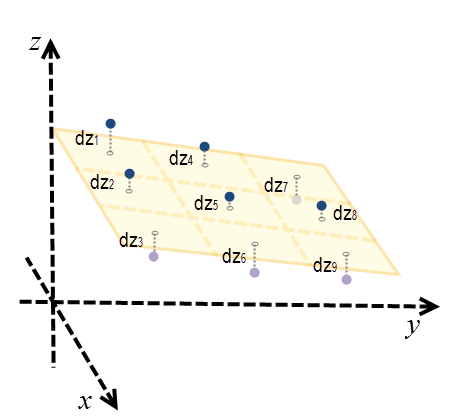
此处，平面表示为 z = Ax + By + C。 对于每个像元中心，dz_i 是实际 z 值与拟合 z 值之间的差值。

如果 ∑⁹_i=1dz_i² 最小，则平面将实现最佳拟合。

对平面进行拟合后，将在像元位置处计算表面法线。 在相同位置，还将计算与椭球体表面的切平面垂直的椭球体法线。

测地线坡向计算

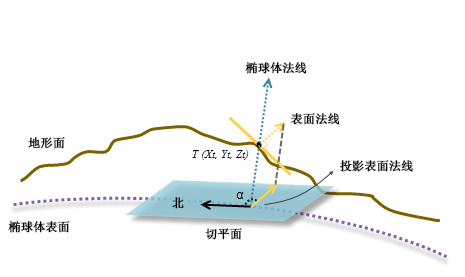
由于将椭球体表面的切平面视为参考平面，因此表面法线将垂直投影到平面上。 最后，通过按顺时针方向测量北向与平面法线的垂直投影之间的角度 α 来计算测地线坡向（请参见上图）。

是否应使用表面参数工具？

如果输入栅格参数值（Python 中的 in_raster）为高分辨率值（其像元大小小于几米，或者特别是存在噪点），请考虑使用表面参数工具及其用户定义的邻域距离选项，而非此工具的直接 3 x 3 邻域。如果输入栅格参数值（Python 中的 in_raster）为高分辨率值（其像元大小小于几米，或者特别是存在噪点），请考虑使用表面参数工具及其用户定义的邻域距离选项，而非此工具的直接 3 x 3 邻域。 使用较大邻域可以最大程度地减少噪点表面的影响。 当使用高分辨率表面时，使用较大邻域也可以更好地表示地形和表面特征。

GPU 的使用

对于测地线方法，如果您的系统上已安装某些 GPU 硬件，则此工具能够显著提高性能。 有关如何支持、配置以及启用此功能的详细信息，请参阅通过 Spatial Analyst 处理 GPU 一节。

参考资料

Marcin Ligas, and Piotr Banasik, 2011. Conversion between Cartesian and geodetic coordinates on a rotational ellipsoid by solving a system of nonlinear equations (GEODESY AND CARTOGRAPHY), Vol. 60, No 2, 2011, pp. 145-159

E.J.Krakiwsky, and D.E.Wells, 1971. Coordinate Systems In Geodesy (GEODESY AND GEOMATICS ENGINEERING, UNB), LECTURE NOTES, No16, 1971, pp. 18-38

Lancaster, P. and Šalkauskas, K. Curve and Surface Fitting: An Introduction. London: Academic Press, 1986.

B. Hofmann-Wellenhof, H. Lichtenegger and J. Collins, 2001. GPS - theory and practice. Section 10.2.1. p. 282.

David Eberly 1999. Least Squares Fitting of Data (Geometric Tools, LLC), pp. 3.