需要 Spatial Analyst 许可。
使用 ArcGIS Spatial Analyst extension,可以通过将栅格像元分组到类或聚类中来创建分类。 类通常是已知类别,例如森林、居民区或水体,而聚类是基于像元属性统计的一组像元。 特征是代表类或聚类的像元子集。 特征的统计信息存储在一个特征文件中,该文件将用于对输入波段交叉点中的所有像元进行分类。
什么是类?
类对应于一组有意义的位置。 比如森林、水、小麦高产都是类。
每个位置的特征都是一组值或矢量,每个变量一个值,或输入波段。 每个位置均可以可视化为多维属性空间中的一个点,其轴对应于输入波段中的变量。 在这个多维属性空间中的一组点被称为一个聚类,在这种情况下,由于聚类指的是一些有意义的内容,因此它也可以被认为是一个类。 如果两个位置的属性(波段值的矢量)相似,则它们属于同一个聚类。
如果类可以通过其属性值来分离或区分,则已知类可以在属性空间中形成聚类。 与属性空间中的自然聚类相对应的位置可以解释为自然发生的地质层类。
识别监督分类的类
在监督分类中,已知要将研究地点划分为哪些类,并且在研究地点中拥有代表每个类的样本位置。 例如,如果根据卫星影像创建土地利用地图,则类可能是城市、水体、森林、田野和道路。 目标是将研究区域中的每个位置分配给一个已知类。 可以识别为属于一个类的样本位置越多,并且像元值在一个类中越均匀,随后的分类就越好。 标识已知类位置的实际位置称为训练样本。
可以在面图层或栅格上识别训练样本。 定义训练样本时,可以将现有栅格标识为参考。 通常情况下,栅格中前三个图层的彩色合成显示为背景,并在生成训练样本时用作识别要包围的区域的参考。
创建非监督分类的类
非监督分类的第一步是创建聚类。 从统计学上讲,聚类是数据中自然发生的分组。 Iso 聚类工具需要输入栅格波段、类数、输出特征文件的名称、迭代次数、最小类大小,以及从中获取用于计算聚类的样本点的间隔(下面讨论了最终三个参数)。
该工具返回一个特征文件,其中包含已识别聚类的像元子集的多元统计信息。 计算结果用于识别像元位置属于哪个聚类、聚类平均值以及方差协方差矩阵。 此信息存储在 ASCII 特征文件中。 特征文件对于剩余未采样像元的聚类和分类至关重要。
存储类或聚类统计信息:特征文件
特征文件是一个 ASCII 文件,它存储了每个感兴趣的类或聚类的多元统计信息。 该文件包括每个类或聚类的平均值、类或聚类中的像元数以及类或聚类的方差协方差矩阵。
可以使用任何文本编辑器显示特征文件。
对于任何类或聚类,在方差协方差矩阵中从左上角移动到右下角的对角线值是对应于输入栅格波段的变量的方差值,输入栅格波段由波段矩阵中的行/列交叉点标识。 矩阵中的所有其他值都是协方差值。
如何确定非监督分类的聚类
用于在非监督分类中创建聚类的算法的名称是 Iso 聚类。 isodata 聚类算法的 Iso 前缀代表迭代自组织 (ISO),这是一种执行聚类的方法。 使用研究区域中的像元子集计算聚类。 所有聚类计算均针对多元属性空间中的像元值执行,不基于任何空间特征。 也就是说,平均值是从不同输入波段的属性值中导出的。 方差和协方差值是根据波段内和波段间的变化计算的。
以下示例使用 K 均值或 ISO 聚类方法。 将使用双波段栅格从理论上解释该方法。 同样的方法适用于输入的尽可能多的波段,或适用于 n 维空间。 以下提供了概念性讨论,可以更好地理解 ISO 聚类方法。
- 绘制一个空图,其中第一个波段中的值范围绘制在 x 轴上,第二个波段中的值范围绘制在 y 轴上。
- 将绘制一条 45 度线并将其划分为指定的类数。 这些线段中的每条线段的中心点是类的初始平均值。
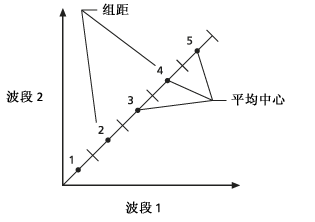
- 将在图表上绘制每个样本像元,并确定该点到 45 度线上每个平均中心点的距离。 使用勾股定理在属性空间中计算距离。 采样本点被分配到由最近的平均中心点表示的聚类。
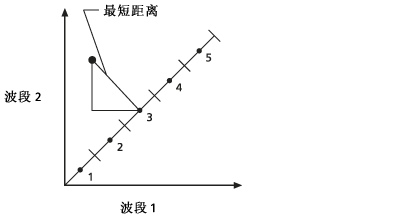
- 绘制下一个采样点,并对所有采样点重复上述过程。
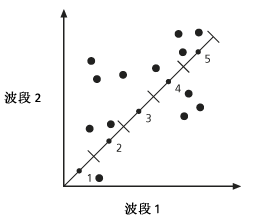
- 将迭代上述过程。 在下一次迭代之前,根据在上一次迭代中当前分配给聚类的像元位置值,为每个聚类计算一个新的平均中心点。 使用每个聚类的新平均中心点,重复前两个步骤。
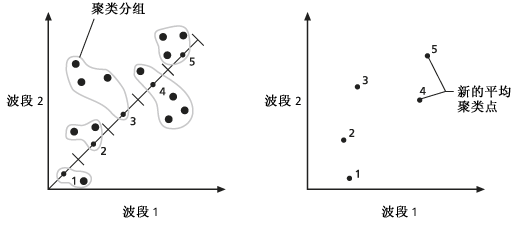
- 将更新平均值,并重复前面的步骤。 更新平均值的迭代过程将持续到达到用户定义的迭代次数,或者直到在一次迭代中相对于新平均值,只有不到 2% 的像元从一个聚类更改为另一个聚类。
聚类对每个波段内的值范围都很敏感。 此值范围用于确定 x 轴和 y 轴上的值,平均值和采样点之间的欧氏距离是根据这些值计算的。 要使各波段的属性数大致相同,各波段的值范围应类似,无论是执行监督分类还是非监督聚类。 当一个波段的值范围相对于其他波段较小时,多元空间中的欧氏距离可能很小,以至于可能导致多个聚类均值为零。 如果任何聚类的均值为零,则最终分类和依赖于特征文件的任何其他多变量工具都将失败。 理想情况下,所有波段都应归一化到相同的值范围。