最佳区域连接工具可标识用于连接一系列输入区域的最低成本路径的最佳网络。 该工具不会创建将一个位置连接到另一位置的单独路径。
如果存在多个区域,并且希望创建网络,从而以最佳方式绘制区域之间的行进路线,请使用此工具。 例如,区域可以是一系列栖息地、公园或伐木场。 生成的网络可以是连接栖息地的野生动物廊道、连接公园的自行车道或连接伐木场的集材道路。
在生成的网络中,旅行者可以使用路径从一个区域移动到任何其他区域,其中包括通过其他区域到达较远的区域。
如果您提供成本表面输入,则生成的网络将是最低成本路径的网络。 如果仅提供输入源,则生成的网络将是最短路径的网络。
在最佳网络中,行进方向无关紧要。 无论旅行者是从一个区域移动到另一个区域,还是从第二个区域移动回第一个区域,累积成本均相同。 如果行进方向与您的分析有关,请使用最佳路径为线工具。
最佳网络应用示例
位置之间的最低成本路径的最佳网络可用于解决各种情况,例如:
- 在赈灾工作中,您已标识将设立救援和医务人员营地的五个区域。 您希望开发营地间补给线路的最佳网络。
- 在木材采伐中,您希望创建用于采伐木材的集材道路的最有效成本网络。
- 在消防行动中,您希望标识在各个总部之间转移消防资源的最佳路线网络。
- 您已经从适用性模型中标识了 10 个短尾猫的最佳栖息地。 您希望短尾猫能够通过最有效的野生动物廊道网络在各斑块间移动,以保持种群的遗传多样性。
最佳网络分析
可以在概念上将距离分析分为以下相关功能领域:
- 计算直线距离,可以选择性地使用障碍或表面栅格调整计算。
- 可以选择使用成本表面、源特征、垂直系数和水平系数来确定遇到距离的比率。 创建累积距离栅格。
- 使用最佳网络、特定路径或廊道连接生成的累积距离表面的区域。
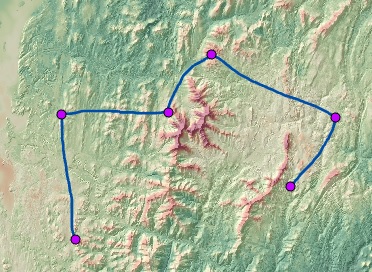
从第三个功能区起,使用最佳路径网络连接区域的过程如下所示。 该方案包括对应于护林员站的 4 个区域(紫色点)和一些河流(蓝线)的集合。
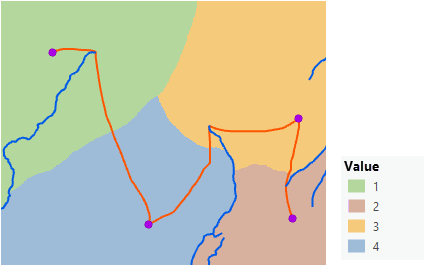
在应用障碍的同时,通过成本表面的最佳网络连接区域。
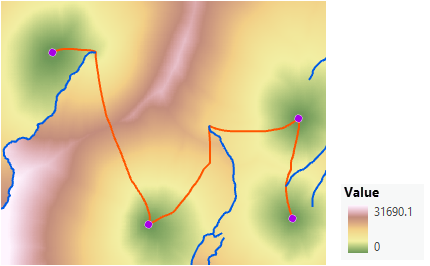
通过检查距离分配输出,可以看出未连接两个下部区域的原因。 由于河流障碍,这些区域不是成本邻域。
创建最佳网络
要创建最佳网络输出,请完成以下步骤:
- 打开最佳区域连接工具。
- 在输入栅格或要素区域数据参数中提供要连接的区域。
- 对输出最佳连通性网络进行命名。
- 还可以提供障碍数据集。
- 如果适用,请为输入成本栅格参数提供成本表面。
- 或者,为相邻连接的输出要素类参数提供名称。
- 也可以指定距离方法或区域内的连接参数值。
- 单击运行。
“最佳区域连接”工具
最佳区域连接工具可标识用于连接一系列输入区域的最低成本路径的最佳网络。
提供输入
首先,标识源区域。
区域可以是点、线、面或栅格像元组。 这些区域可标识要连接的位置。 要素数据集中的位置被视为区域。 当输入为栅格时,区域是具有相同值的连续像元组。
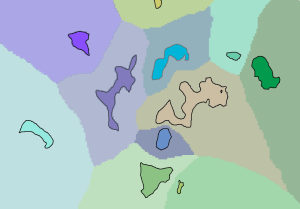
在下图中,输入区域(彩色面)显示在成本表面图层上。
确定最低成本区域
使用距离分配工具执行的计算来为每个非源像元标识最低成本区域。
在下图中,输入区域显示在相关距离分配图层上。 分配栅格中的各像元值可标识可达到最低累积成本的区域。
创建成本路径
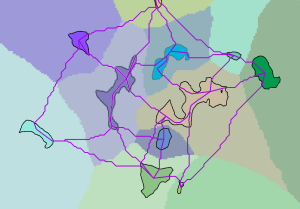
在各区域及其相邻成本区域之间创建成本路径。
在下图中,输入区域以及从各区域到其相邻成本区域的最低成本路径(洋红色的线)显示在相关成本分配图层上。
将区域和路径转换为图形
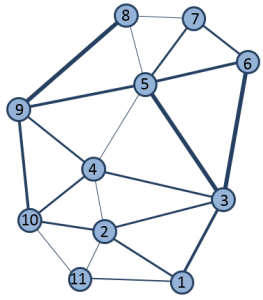
将区域和生成的路径转换为图形。 在这种情况下,图形是用于通过图论对成对关系进行建模的数学结构。 在转换中,区域为折点,路径为边。 路径的累积成本为边的权重。
从概念上讲,此转换由以下图示表示。 带有编号的圆圈为折点(区域),折点间的连接线为边(最低成本路径)。 边的权重为路径的累积成本。 在图示中,较高的成本用粗线表示。
注:
要完全理解该工具的工作原理,建议您首先对图论进行一些基本的了解。 许多资源适用于此,然而,您可以从此处的“维基百科”条目开始:https://en.wikipedia.org/wiki/Graph_theory。
通过图论确定最小跨度树,以便用效果最佳(成本最低)的方式连接折点(区域)。 最小跨度树不一定是唯一的,原因在于可能有多组边被视为最佳边。
注:
可在线查看有关最小跨度树的更多详细信息,例如此处的“维基百科”条目:https://en.wikipedia.org/wiki/Minimum_spanning_tree。
映射到线要素
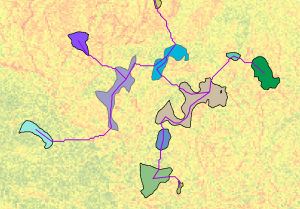
最小跨度树的区域和路径的空间表达将映射回输出要素类。
在下图中,最小跨度树的输入区域和最低成本路径网络(洋红色线)显示在相关成本表面图层上。
相邻成本区域的输出路径
此外,相邻成本区域的路径要素类可以作为输出。 您可以使用此输出来创建自己的网络、为最小跨度树添加路径或在 Network Analyst

如果未提供成本表面,则输出将是以最短方式连接区域的路径网络。
注:
最佳区域连接工具支持障碍。 障碍可以由障碍参数或掩膜或成本表面栅格中的 NoData 像元指定。 生成的网络确定了从源到达每个位置的最短或成本最低的绕过障碍的物理距离。
其他信息
以下部分包含有关通过最佳路径网络连接区域的其他信息。
路径延续通过区域
每个路径都将作为单独的线性要素,并且在路径通过公共线段处存在重复的线。
对于连接的路径网络,如果输入区域是面或多像元区域的栅格,则路径可延续到该区域内的点以允许旅行者通过一个路径进入、在区域内移动并从其他路径离开,从而到达其他区域。 由于不了解旅行者将如何在该区域内移动,因此在该区域内没有将成本分配给这些扩展线段,并且在该区域内移动时不会产生任何成本。 这同样适用于线性区域为输入的情况 - 沿线性区域移动到其他路径也不会产生任何成本。
为了说明相对于一系列独立的最低成本路径的生成连接网络,下图显示了可以连接区域的两种方式之间的差异。 第一个图像显示了使用距离累积工具的输出作为最佳路径为线工具的输入的结果。 在这种情况下,路径仅可以到达区域边缘。 第二个图像显示了最佳区域连接工具创建的路径(用于连接区域)的生成网络。 在此结果中,路径在区域内延续以使旅行者通过一个路径进入区域并从另一路径离开。

由于最佳区域连接的输出为具有正确拓扑的网络,因此可以在 Network Analyst中使用该输出执行其他分析。
借助最佳区域连接工具,您还可以通过为区域内的连接参数指定无连接来防止路径继续通过区域。
最佳区域连接和最佳路径为线工具
最佳区域连接工具可在多个输入区域之间创建路径的最佳网络。 将距离累积与最佳路径为线工具结合使用,以在标识的源和目的地之间创建路径。 通过迭代式隔离区域(作为源)并将其连接到标识为目的地的其他区域,也可以使用距离累积和最佳路径为线工具序列来创建路径网络。 将对每个区域重复该过程,并对所生成的最小成本路径进行合并。
迭代方法的限制如下:
- 将每个区域连接到所有其他区域是一个组合过程,可创建大量路径,尤其是在存在大量区域时。 此方法不允许通过使用一系列路径连接较远区域,这些路径可连接您和较远区域之间的一系列区域。
- 要降低生成大量路径的可能性,可以多次使用两个区域之间最近的直线距离标识源和目的地。 但是,尽管两个区域在地理位置上可能彼此靠近,但由于存在诸如山峰或河流之类的中间要素,因此在两个区域之间旅行可能会很昂贵。 最佳区域连接工具可根据最低成本邻域来确定要连接的区域。
- 可以多次连接不同区域的不同路径,并且这些路径会沿着至公共区域的同一最低成本路径。 如果共享部分为栅格路径(例如,由最佳路径为栅格工具创建的栅格路径),则难以对其进行分析。 执行后续分析时,最好将每个路径视为独立的实体。
- 由最佳路径为线工具创建的路径仅会到达区域的边缘。 该工具不会创建连接的路径网络。
区域和分区
区域可用作最佳区域连接的输入。 区域可以是要素或栅格数据集。 如果输入区域是要素数据,则要素将转换为栅格。 区域是具有相同像元值的任何连续像元组。 分区是栅格中所有具有相同值的像元。 区域可以由单个区域或多个断开的分区组成。 对于最佳区域连接,如果输入中存在未彼此连接且具有相同值的像元组,则将其视为具有断开连接的像元的单个区域。 结果是,将仅在网络中连接成本最低的区域内的一组像元,因此并非输入中的所有像元都会进行连接。
可使用区域组工具将包含多个断开连接的像元组的输入转换为一系列独立的区域。 使用区域组的输出作为最佳区域连接的输入会将每个区域连接到所有其他区域,因此可通过生成的网络访问输入中的所有像元。
使用最佳区域连接工具的示例场景
以下是使用最佳区域连接工具的常见场景。
- 最佳网络(最小跨度树)为所需输出。
- 使用距离累积和最佳路径为线将特定路径添加到最佳网络中,以连接最佳网络未捕获的区域。 例如,在扑灭多场森林火灾时,请增加逃生路径,以供消防员在情况变化时使用。
- 从到相邻区域的所有路径的可选输出中创建网络。 使用选择工具以选择路径。
- 将上述任一情景转换为 Network Analyst 网络,并对区域间的移动执行其他分析。