分区统计工具的工作原理

分区统计操作是一种用于计算由另一个数据集定义的区域内的栅格（值栅格）的像元值的统计操作。 有两种工具可以按区域计算统计数据，分区统计和以表格显示分区统计。

分区统计工具一次仅计算一个统计数据，并创建一个栅格输出。 该值变为与该区域相对应的像元的栅格输出的像元值。 如果区域要素包含重叠区域，则仅针对一个区域计算统计数据，因为输出栅格中的像元只能表示一个值。

以表格显示分区统计工具使用预定义子集或所有统计数据来计算一个或多个统计数据，并创建表输出。 与分区统计相同，得到的统计数据是每个区域的单个值。 输出表中每个区域都有一条记录，并且统计值是在预定义字段中进行报告。 如果区域输入是要素，并且包含重叠区域，则将计算所有区域的统计数据，并在每个区域的单独记录中报告输出。

输入区域图层将定义区域的形状、值和位置，其可以是栅格或要素。 在分区操作期间，要素数据首先会被转换为栅格。 在栅格数据中，区域是所有具有相同值的像元，无论它们是否是连续。 每个区域必须具有唯一标识，并且如果其是栅格，则必须具有整型数据类型。 可以指定区域输入中唯一值的任何整型或字符串型字段来定义区域。

输入值栅格中包含了用于计算各区域的输出统计数据的值。 可以是整型或浮点数据型。

在以下图示中，将为每个区域指定输入值的最大值。

将显示分区统计的输入和输出示例。 浅灰色像元表示 NoData。

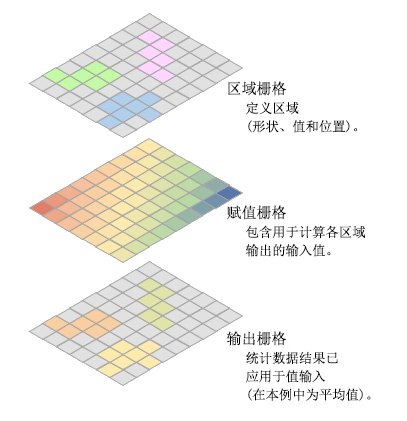
如何为栅格区域识别值栅格中的像元

为了计算统计数据，该工具首先从每个区域内的所有像元的值栅格中提取像元值。 区域内值栅格中的像元识别是通过叠加值栅格上的区域来完成的。 当区域和值输入都是相同像元大小的栅格并且像元已对齐时，将提取叠加该区域的像元的值栅格的像元值，并计算统计数据。

叠加在值栅格上的区域栅格，其中突出显示了所提取的像元

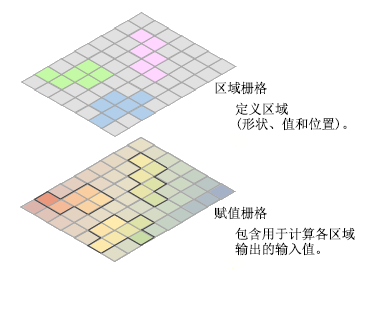
当区域栅格的像元大小或对齐方式与值栅格的像元大小或对齐方式不同时，区域栅格和值栅格之间的像元将无法彼此完美地叠加。 然后，该工具将在内部调整一个或两个栅格，以实现像元的完美叠加。 此调整可遵循一些简单规则来进行。 如果区域栅格的像元大小与值栅格的像元大小不同，则输出像元大小的值将为输入的最大值，且值栅格将在内部用作捕捉栅格。 如果像元大小相同，但像元不对齐，则值栅格将在内部用作捕捉栅格。 在执行区域操作之前，上述任一情况都会触发内部重采样。

像元大小、捕捉栅格、输出坐标系或这些选项的组合，将在地理处理环境设置中进行指定，分区操作将在通过使用这些设置创建的分析窗口中执行。 有关详细信息，请参阅如何在 Spatial Analyst 中确定分析窗口。

如何为要素区域识别值栅格中的像元

在本质上，分区操作是对两个栅格进行的栅格分析，其中一个是区域，另一个是值。 如果区域是由要素定义，则将发生内部要素到栅格的转换。 面区域的内部转换将在面转栅格工具使用像元中心法来通过像元大小和值栅格的捕捉栅格栅格化输入。 当栅格化网格的像元中心都不位于要素区域内时，这可能导致输出中缺失区域的意外结果。 这可能会在小于内部区域栅格像元区域的区域以及较大的区域中发生。

在下面的示例中，图 (1) 表示输入要素区域、输入值栅格及其像元中心。 输入要素具有三个区域（黄色形状），以下表述均为真：

• zone1 大于单个像元。
• zone2 和 zone3 小于一个像元。
• 像元中心位于 zone2 之外，但在 zone3 之内。

在图 (2) 的区域栅格化过程中，因为没有像元中心位于 zone1 和 zone2 内部，只有 zone3 被栅格化，并且其他两个区域基本消失。

显示了在计算分区统计数据的同时对要素区域进行的内部转换。

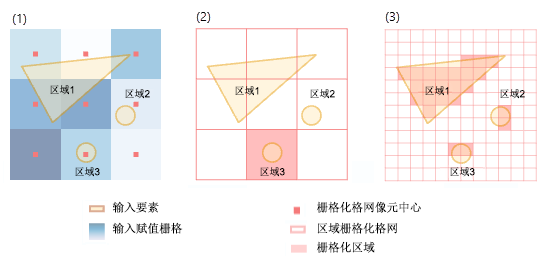
为避免区域从输出中消失，请确保每个区域都包含来自值栅格的一个或多个像元中心。 这样做的方法之一是通过在环境中指定较小的像元大小来创建更多像元中心。 默认情况下，分析像元大小为值栅格的大小。 但是，如果您在分析环境中指定的像元大小小于值栅格的像元大小，您将启用更多要被捕获的区域，如上面的图 (3) 所示。 切记指定像元大小越小，生成的输出栅格越大。 较高的分辨率输出并不一定像看起来那样高质量，因为其他详细信息实际上没有存在于输入值栅格中。

使用值栅格的相同像元大小和像元对齐将要素区域转换为栅格区域后，即可通过将区域叠加在值栅格上来从区域中的值栅格提取像元。

当在地理处理环境设置中指定像元大小、捕捉栅格、输出坐标系或这些要素的组合时，将在这些设置所定义的分析窗口中执行分区操作（包括内部要素到栅格的转换）。 要了解详细信息，请参阅如何在 Spatial Analyst 中确定分析窗口。

计算算术和圆形统计数据

通过对所有像元值求和并除以像元数来计算平均值可能适用于高程等数据。 但是，如果您的数据表示诸如坡向（0 度到 360 度的罗盘方向，以度为单位）或一天中的小时数（0 到 24 小时）等循环量，则计算算术平均值会产生错误输出，因为最小值和最大值代表相同的数量。 对于这种数据，需要计算圆形统计数据。

例如，如果您要计算两个像元值（0 度和 360 度）的平均值，则算术平均值将为 180 度。 这是不正确的，因为 0 度和 360 度代表相同的罗盘方向。 可以通过计算圆形平均值来获得正确的统计数据，该平均值将为 0 度。

您可以通过选中计算圆形统计数据（Python 中的 circular_calculation = "CIRCULAR"）参数来指定圆形统计数据计算。 计算圆形统计数据时，需注意表示循环数据的最低和最高值。 最低值假定为 0。 最高值可以指定为圆换行值 (circular_wrap_value in Python) 参数。 此参数的默认值为 360。

根据您的数据类型，选择统计数据计算类型，并为圆形统计数据选择适当的圆换行值，以获得正确的输出。 支持以下循环统计数据：平均值、众数、少数、标准差和变异度。

使用多维栅格计算分区统计

多维栅格数据表示位于多个时间以及多个深度或高度的数据。 此类数据通常用于大气、海洋和地球科学，并且可以通过监控平台进行观察、由卫星捕获或从使用各种统计技术对数据进行处理、聚合或插值的数值模拟模型生成。 有关多维栅格的详细信息，请参阅多维栅格数据概览。

分区统计和以表格显示分区统计工具支持多维区域和值栅格数据作为输入。 当选中以多维方式处理参数（Python 内 process_as_multidimensional 参数中的 ALL_SLICES）时，将计算多维栅格的所有切片的分区统计。 如果未选中以多维方式处理参数（Python 中的 CURRENT_SLICES），仅会处理当前切片。

对多维数据进行分区统计分析的示例包括：

• 气象学家希望了解特定时间段的飓风运动和沿飓风轨迹线的降水分布。 在分区统计工具中使用多维处理，气象学家可以了解随时间变化的飓风区域每个时间片的平均降水量。
• 生态学家希望从特定流域过去 30 年的每日最大降雨量数据中查看极端事件的分布。 具有百分位数值列表的百分位数统计类型的以表格显示分区统计工具可用于在以多维方式处理时，查看时间序列数据的最大每日降雨量数据的分布。

受支持的多维栅格数据类型包括多维栅格图层、多维镶嵌、图像服务以及 Esri 的云栅格格式 (CRF)。

要在 ArcGIS AllSource 中添加多维栅格图层，请在地图选项卡的图层组中，单击添加数据中的多维栅格图层选项。 或者，使用创建多维栅格图层工具，为分区操作选择适当的变量，并生成多维栅格图层。

分区统计多维输出

当您指定分区统计工具将以多维方式处理输入时，该工具将创建多维栅格输出。 在区域栅格的切片与值栅格中当前变量的切片之间进行逐个切片的分区操作。 计算出的统计值将存储在多维变量中，该多维变量的名称是通过组合值栅格中的变量名称和要计算的统计数据而创建的。 输出变量的维度数和切片数取决于区域和值栅格输入的特定性质。

您可以从属性窗格浏览栅格输出的多维信息。

对于以表格显示分区统计，当您指定将以多维方式处理数据时，它将生成一个平面表输出，其中包含为所有区域和切片计算的统计数据。 该表将包括其他字段，以指示变量名称、维度名称及其值，以及为每个区域计算的统计数据。

由于多维处理是在区域栅格和值栅格之间逐个切片进行的，因此来自分区统计工具的输出多维栅格中的切片数和来自以表格显示分区统计工具的输出表中的记录数，将取决于其中的输入栅格类型和切片数。 以下小节描述了示例。

具有相同维度的多维区域和值栅格

要查找相应深度处的各种温度范围内不同海洋深度处的最大盐度，需要执行分区统计，其中多维区域代表温度区域，而多维值栅格则代表盐度。 将对具有来自值栅格的相应切片的每个区域切片执行分区操作。 输出多维栅格将具有与值栅格相同的切片数量。

在下图中，区域和值栅格中的变量具有相同的三个维度 x、y 和 d，并且维度值 d₀、d₁ 和 d₂ 处的切片数相同。 输出多维栅格中的变量还将具有相同的三个维度 x、y 和 d，并且在维度值 d₀、d₁ 和 d₂ 处具有相同数量的切片。

将显示具有生成的分区统计栅格的相同维度的多维区域和值输入栅格。

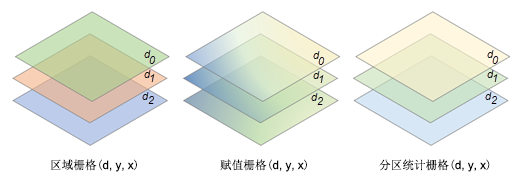
可通过添加每个切片中的区域数来确定以表格显示分区统计输出中的记录总数。 如果 d₀、d₁ 和 d₂ 深处的区域数分别为 5、4 和 3，则记录总数将为 12 (5 + 4 + 3 = 12)。

具有不同维度的多维区域和值栅格

可以通过执行分区统计来确定用于部署资产（例如，遥控操作潜水艇 (ROV)）的合适位置和时间窗口，其中多维区域表示 ROV 在不同时间的潜在位置，而多维值栅格（例如混合坐标海洋模型 (HYCOM) 模型输出）表示不同深度和时间的洋流。

将使用值栅格中的每个切片为区域栅格中的每个切片执行分区操作。 通过将区域栅格中的切片数乘以值栅格中的切片数，可以确定输出多维栅格中的切片数。

在下图中，区域栅格中的变量具有三个维度 x、y 和 d，并且在维度值 d₀、d₁ 和 d₂ 处具有三个切片。 值栅格中的变量具有三个维度 x、y 和 t，并且在维度值 t₀ 和 t₁ 处具有两个切片。 输出多维栅格中的变量也将具有四个维度 x、y、d 和 t。

将显示具有生成的分区统计栅格的不同维度的多维区域和值输入栅格。

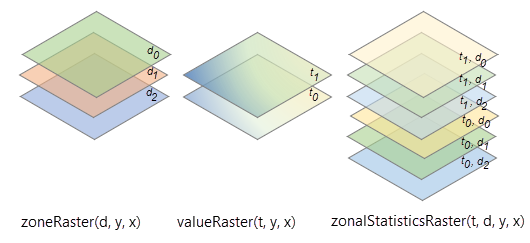
可通过将区域栅格中的深度数乘以值栅格中的时间步长数来确定区域统计工具输出中的切片总数，在本示例中，该值将为 6（3 个深度 x 2 倍 = 6）。 可通过乘以每个切片中的区域数来确定以表格显示分区统计输出中的记录总数。 如果区域数为 5，则本示例中的记录总数将为 30（5 个区域 x 3 个深度 x 2 倍 = 30）。

仅限多维值栅格

要查找一年中每个县每天的最高温度，将需要执行分区统计，其中多维值栅格表示每日温度，而区域栅格则表示县。 将使用相同区域栅格为值栅格中的每个切片执行分区操作。 输出多维栅格将具有与值栅格相同的切片数量。

在下图中，值栅格中的变量具有三个维度 x、y 和 t，并且在维度值 t₀、t₁ 和 t₂ 处具有三个切片。 输出多维栅格中的变量还将具有相同的三个维度 x、y 和 t，并且在维度值 t₀、t₁ 和 t₂ 处具有相同数量的切片。

将显示多维值栅格处理。

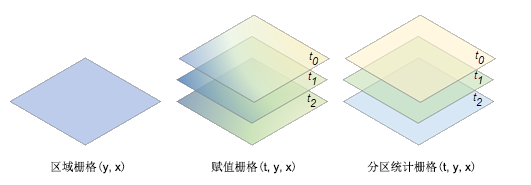
可通过将区域数和值栅格中的切片数相乘来确定以表格显示分区统计输出中的记录总数。 如果区域数为 5，则记录总数将为 15 (5 x 3 =15)。

仅限多维区域栅格

要查找每个随时间变化的洪泛区类别中十年最大降水量的平均值（该平均值随着时间的推移而变化）以进行生态景观规划，将需要执行分区统计，其中多维区域栅格表示洪泛区，而价值栅格则表示十年最大降水量。 将使用相同值栅格为来自区域栅格的每个切片执行分区操作。 输出多维栅格将具有与区域栅格相同的切片数量。

在下图中，区域栅格中的变量具有三个维度 x、y 和 t，并且在维度值 t₀、t₁ 和 t₂ 处具有三个切片。 输出多维栅格中的变量还将具有相同的三个维度 x、y 和 t，并且在维度值 t₀、t₁ 和 t₂ 处具有相同数量的切片。

将显示多维区域栅格处理。

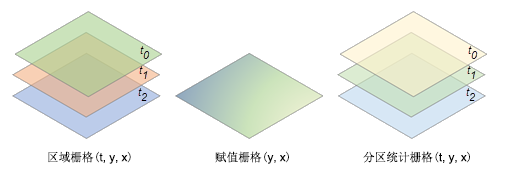
可通过将区域数和区域栅格中的切片数相乘来确定以表格显示分区统计输出中的记录总数。 如果区域数为 5，则记录总数将为 15 (5 x 3 =15)。

统计分析

下面列出了可用于计算分区统计的统计数据类型，其中包含其他详细信息，以及一个显示了示例输入中每个选项的结果的图解说明。

众数

• 将每个区域中最常出现的值分配到该区域的所有像元中。
• 当区域中的众数值存在平局（存在多个具有最高出现频率的值）时，会将值最小的平局值指定为该区域中所有像元位置的输出。

示例：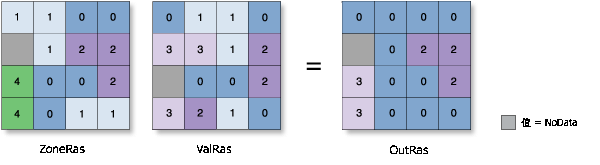

OutRas = ZonalStatistics(ZoneRas, "VALUE", ValRas, "Majority")

最大值

• 将每个区域中的最高值分配到该区域的所有像元中。

示例：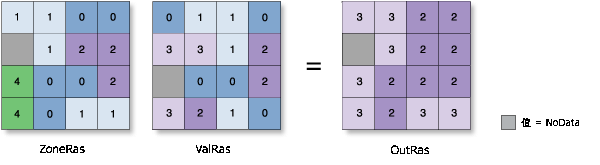

OutRas = ZonalStatistics(ZoneRas, "VALUE", ValRas, "Maximum")

平均值

• 将每个区域的平均值分配给该区域中的所有输出像元。
• 算术平均值的公式如下：

  

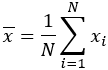
  其中：

  • x̄ = 平均值
  • x_i = 观测值
  • N = 观测值个数
• 圆平均值的公式如下：

  

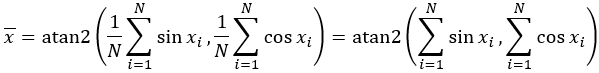
  其中：

  • x̄ = 圆平均值
  • x_i = 观测值
  • N = 观测值个数

  在 Σsin x_i 和 Σcos x_i 均等于 0 的退化情况下，将使用特殊值 -1，表示无法正确定义圆平均值。

示例：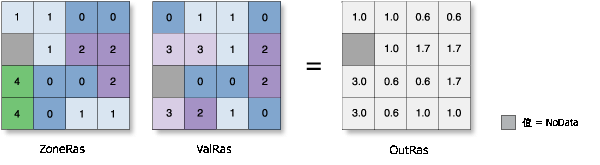

OutRas = ZonalStatistics(ZoneRas, "VALUE", ValRas, "Mean")

中值

• 将每个区域的中值分配给该区域中的所有输出像元。
• 统计类型值使用来自 Hyndman and Fan (1996) 的方法 Q1 进行计算。 当两个排序值同样接近目标中值时，将选择两个值中的较小者。
• 要计算中值，需要对区域中的所有像元进行分级。 如果区域中有 n 个像元且 n 为奇数，则将中间的 ((n+1)/2) 值写入该区域的所有像元。 如果像元数为偶数，则输出值为 (n/2)。

示例：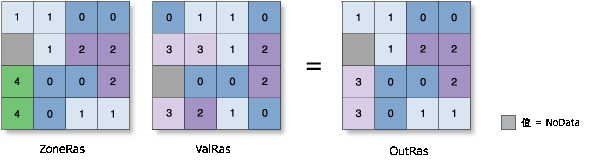

OutRas = ZonalStatistics(ZoneRas, "VALUE", ValRas, "Median")

最小值

• 将每个区域中的最低值分配到该区域的所有像元中。

示例：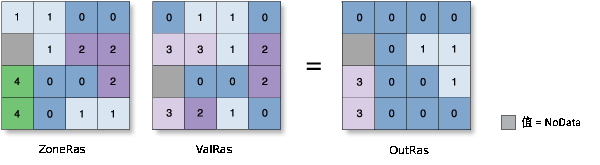

OutRas = ZonalStatistics(ZoneRas, "VALUE", ValRas, "Minimum")

少数

• 将每个区域中最不常出现的值分配到该区域的所有像元中。
• 当区域中的少数值存在平局（存在多个具有最高出现频率的值）时，会将值最小的平局值指定为该区域中所有像元位置的输出。

示例：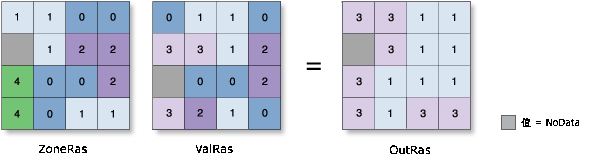

OutRas = ZonalStatistics(ZoneRas, "VALUE", ValRas, "Minority")

百分比数

• 将每个区域中的值的百分比数分配给该区域中的所有输出像元。
• 此统计类型值使用来自 Hyndman and Fan (1996) 的方法 Q1 进行计算。 当两个排序值同样接近目标中值时，将选择两个值中的较小者。
• 为了计算百分位数，使用以下公式将值栅格中的所有像元划分等级：R = P/100 x (n - 1) +1，其中 P 是所需的百分位数，n 是像元数。

示例：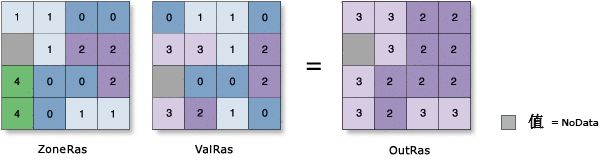

OutRas = ZonalStatistics(ZoneRas, "VALUE", ValRas, "Percentile")

范围

• 将每个区域中最大值和最小值之间的差值分配给该区域的所有像元。
• 范围的定义如下：

  分区范围 = 最大分区 - 最小分区

示例：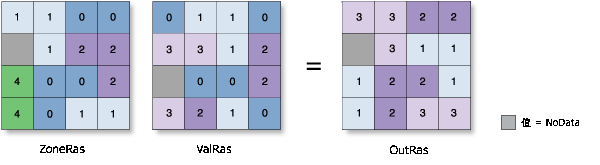

OutRas = ZonalStatistics(ZoneRas, "VALUE", ValRas, "Range")

标准差

• 将每个区域的标准差分配给该区域的所有像元。
• 算术标准差的公式如下：

  

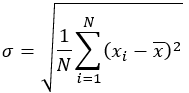
  其中：

  • σ = 标准差
  • x_i = 观测值
  • x̄ = 平均值
  • N = 观测值个数

  注：

  标准差是在整个总体（“N”方法）上计算求得，而不是在样本（N-1 方法）上进行估算。 作为对比，标准差的计算相当于 Microsoft Excel 中的 STDEVP 方法而不是 STDEV 方法。

• 圆形标准差的公式如下：

  

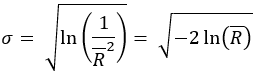
  其中：

  • σ = 圆形标准差
  • R̄ = 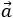的平均结果长度

    在以度为单位的 n 个角度的样本中，汇总了 a₁、a₂、...、a_n的角度，每个角度由一个单位矢量表示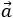， 指向对应的观测方向。

示例：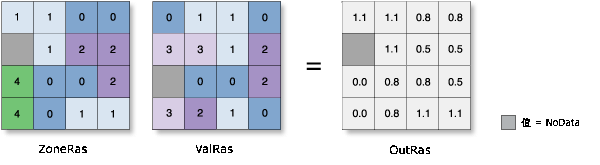

OutRas = ZonalStatistics(ZoneRas, "VALUE", ValRas, "STD")

总和

• 将每个区域中所有像元值的总和分配到该区域的所有像元中。
• 输出栅格的数据类型为浮点型。 这是因为总和值往往很大，并且可能无法用整数值表示。

  请考虑这样的例子：某区域行和列都是 2,500 个像元，像元的值都是 1,000。 这个区域的总和将是 2,500 x 2,500 x 1,000 = 6,250,000,000。 如果需要获得整型输出，且范围在 ± 21.47 亿之间时，可以应用转为整型工具。

示例：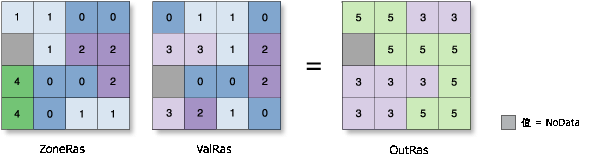

OutRas = ZonalStatistics(ZoneRas, "VALUE", ValRas, "Sum")

变异度

• 将每个区域中唯一值数量分配到该区域的所有像元中。

示例：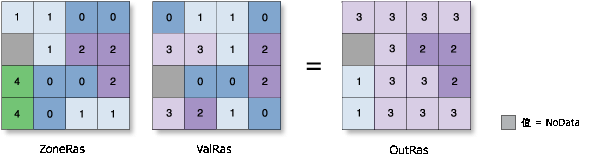

OutRas = ZonalStatistics(ZoneRas, "VALUE", ValRas, "Variety")

输出数据类型

输出数据类型（整型或浮点型）将由所执行的分区计算以及输入值栅格类型决定。 下表标识了输出栅格的预期数据类型：

统计的输入和输出类型

统计	值输入类型	输出
众数	整型*	整型
最大值	整型、浮点型	与输入相同
平均值	整型、浮点型	浮点型
中值	整型、浮点型	整型
最小值	整型、浮点型	与输入相同
少数	整型*	整型
百分比数	整型、浮点型	整型
范围	整型、浮点型	与输入相同
标准差	整型、浮点型	浮点型
总和	整型、浮点型	浮点型
变异度	整型*	整型

注：

* 仅支持整型。

如果“区域”数据集中某像元位置是 NoData，则该位置在输出中将指定为 NoData。

参考资料

Rob J. Hyndman and Yanan Fan (1996) "Sample Quantiles in Statistical Packages" The American Statistician, Vol. 50, No. 4 (Nov., 1996), pp. 361-365.