模糊隶属度工具基于属于指定集合的可能性将输入数据重分类或转换为 0 到 1 等级。 0 将分配给绝对不属于指定集合的位置,1 将分配给绝对属于指定集合的值,0 到 1 之间的整个可能性范围将分配给某个可能隶属度级别(数值越大,可能性越高)。
可以通过 ArcGIS Spatial Analyst extension 中可用的任意数量的函数和运算符来变换输入值,这些函数和运算符可将值重分类为 0 到 1 可能性等级。 但是,借助模糊隶属度工具,您可以基于模糊化过程中常见的一系列特定函数来变换连续输入数据。 例如,模糊线性隶属度函数基于 0 到 1 等级对输入值进行线性变换,其中 0 将分配给最小输入值,1 将分配给最大输入值。 所有中间值都会收到一些基于线性等级的隶属度值,输入值越大,则被分配的可能性越大,或者更接近于 1。
在脚本中,这些函数中的每个函数都将作为 Python 类实现。
由于这些隶属度函数特定于连续输入数据,因此,如果您希望使用类别数据作为“模糊叠加”分析的输入,则需要使用任意数量的 Spatial Analyst 工具将数据变换为 0 到 1 隶属度可能性等级。 对于此过程,最有用的两个工具为重分类和划分。 借助重分类工具,您可以将类别数据变换为 0 到 10 等级(您无法使用此工具将数据直接重分类为 0 到 1 等级),然后将变换后的数据除以 10 以获得 0 到 1 等级。
每个隶属度函数的公式和应用各不相同。 要使用的函数将取决于哪种函数最能捕获基于正在建模的现象的数据变换。 您可通过一系列输入参数进一步优化各个隶属度函数的特征。
以下列出了不同的模糊隶属度函数及其最佳用途。 每个函数都附有图表。 x 轴上为输入值(在图表中称为明确值),y 轴上为变换后的模糊隶属度值。
模糊隶属度类型
以下将对 7 个模糊隶属度函数中每个函数进行讨论。
Fuzzy Gaussian
Fuzzy Gaussian 函数可将原始值变换到正态分布中。 正态分布的中点用于定义集合的理想定义,将分配 1,其余输入值随着它们同时在正方向和负方向上远离中点,其隶属度将减小。 输入值的隶属度从中点开始减小,直到它们到达某个点,在该点上,值与理想定义相距过远,并且肯定不在集合中,因此将分配 0。
更改散度参数将更改过渡区的宽度和特征。
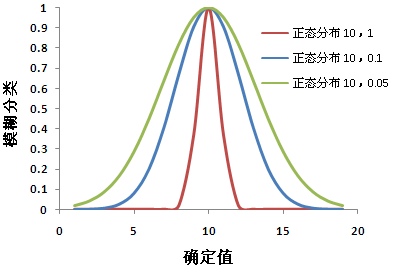
高斯函数在特定值的附近进行分类时十分有用。 例如,在房屋适宜性模型中,对于太阳能增益,南向(180 度)可能是理想的建筑方位,小于或大于 180 度的方位不太有利或者不太可能属于理想的适宜性集合。
Fuzzy Large
当较大的输入值更有可能隶属于集合时,可以使用 Fuzzy Large 变换函数。 已定义的中点用于标识交叉点(已分配隶属度 0.5),高于中点的值更可能隶属于集合,而低于中点的值具有递减的隶属度。 散度参数用于定义过渡区的形状和特征。
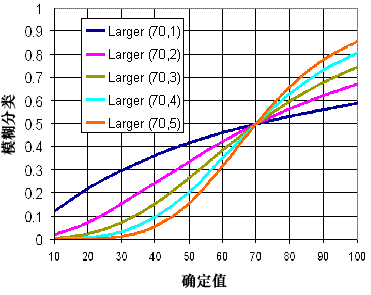
在房屋适宜性模型中,Fuzzy Large 函数可用于变换距垃圾填埋场图层的距离值。 位置距离垃圾填埋场越远,则其越可能隶属于有利适宜性集合。
Fuzzy Linear
Fuzzy Linear 变换函数将在用户指定的最小值和最大值之间应用线性函数。 任何低于最小值的值都将分配 0(绝对不隶属于),任何高于最大值的值都将分配 1(肯定隶属于)。 下图中的蓝线表示正斜率线性变换,其中最小值为 30,最大值为 80。 任何低于 30 的值都将分配 0,任何高于 80 的值都将分配 1。
如果最小值大于最大值,则建立负线性关系(负斜率)。 下图中的红线表示负斜率线性变换。 任何低于 30 的值都将分配 1,任何高于 80 的值都将分配 0。
线的斜率增大或减小的位置定义了过渡区域(下图中的 30 到 80 之间)。
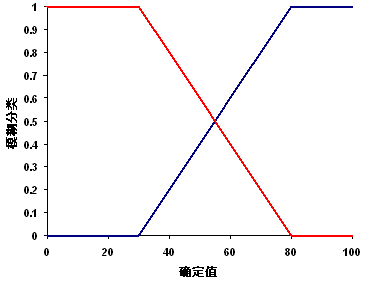
房屋适宜性示例中的 Fuzzy Linear 变换函数可用于到休闲区的距离条件(负线性变换)。 休闲区 500 米范围内的任何位置肯定位于有利的合适集合中;500 到 10,000 米范围内的位置位于合适集合中的可能性将线性下降;超过 10,000 米的任何位置距离休闲区过远,不可能隶属于有利集合,并且将分配 0。
Fuzzy MS Large
Fuzzy MS Large 变换函数类似于 Fuzzy Large 函数,不同之处在于此函数的定义基于指定的平均值和标准差。 通常,这两个函数之间的区别在于,如果极大值更有可能隶属于集合,则 Fuzzy MS Large 函数更为适用。

结果可能类似于 Large 函数,具体取决于已定义的平均值和标准差。
Fuzzy MS Small
Fuzzy MS Small 变换函数类似于 Fuzzy Small 函数,不同之处在于此函数的定义基于指定的平均值和标准差。 通常,这两个函数之间的区别在于,如果极小值更有可能隶属于集合,则 Fuzzy MS Small 函数更为适用。
结果可能类似于 Small 函数,具体取决于平均值和标准差的乘数定义方式。
Fuzzy Near
如果隶属度接近特定值,则 Fuzzy Near 变换函数最适用。 此函数由一个中点定义,该中点定义了集合的中心,标识了确定的隶属度,因此将分配 1。 随着值从中点开始在正方向和负方向上移动,隶属度将递减,直至其为 0 为止,即定义非隶属度。 散度用于定义过渡区的宽度和特征。
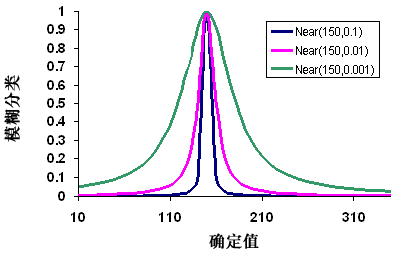
Fuzzy Near 和 Fuzzy Gaussian 可以相似,具体取决于指定的参数。 与 Fuzzy Gaussian 函数相比,Fuzzy Near 函数通常以更快的速度递减,并且具有更窄的分布,因此在非常接近中点的值更可能隶属于集合时使用。
Fuzzy Small
当较小的输入值更有可能隶属于集合时,可以使用 Fuzzy Small 变换函数。 已定义的中点用于标识交叉点(已分配隶属度 0.5),高于中点的值隶属于集合的可能性较低,而低于中点的值隶属于集合的可能性较高。 散度参数用于定义过渡区的形状和特征。
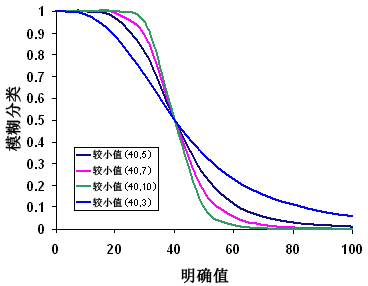
房屋适宜性示例中的 Fuzzy Small 变换函数可用于到电力线的距离条件。 随着到电力线距离的增加,电力接入的成本将更高,因此这些位置不太可能隶属于有利的合适集合。 未将电力接入条件建模为线性变换,以考虑随着距离的增加对电力变压器的需求。