Стандартный способ измерения тренда для набора точек или областей – расчет стандартного расстояния отдельно в измерениях x, y и z. Эти две величины определяют оси эллипса (или эллипсоида), отражающего распределение объектов. Такой эллипс носит название эллипса стандартных отклонений, т.к. метод рассчитывает стандартные отклонения х и у координат от среднего центра, чтобы определить оси эллипса. В 3D также вычисляются стандартные отклонения z-координат от среднего центра, а результат вычисления носит название эллипсоида стандартных отклонений. Эллипс или эллипсоид позволяет увидеть, вытянуто ли распределение объектов и отсюда определить точную ориентацию.
Несмотря на то, что вы можете иметь представление об ориентации путем рисования объектов на карте, расчет эллипса стандартных отклонения делает тренд более явным. Вы можете рассчитать эллипс стандартных отклонений, используя или местоположение объектов или местоположения, на которых оказывают влияние значения атрибутов, связанных с объектами. Последнее относится к взвешенному эллипсу стандартных отклонений.
Вычисления
Эллипс стандартного отклонения рассчитывается по следующим формулам:
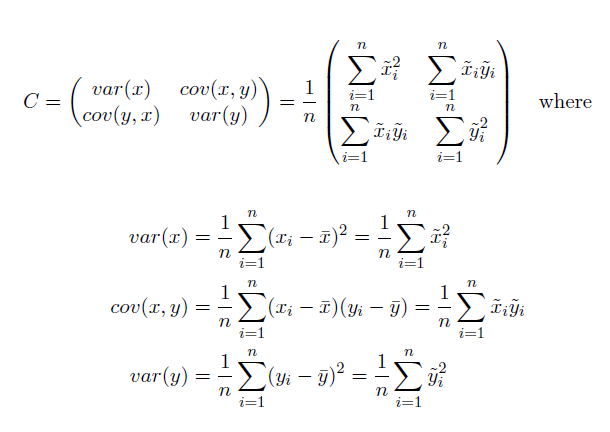
Где x и y – координаты объекта i, {x̄, ȳ} соответствуют Среднему центру объектов, а n- общее их число.
Приведенная ковариационная матрица учитывается в стандартной форме, что приводит к тому, что матрица представлена ее собственными значениями и собственными векторами. Тогда стандартные отклонения для осей x и y:
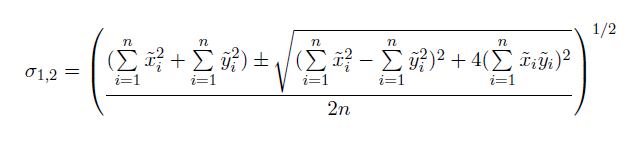
Эти уравнения можно расширить для трехмерных данных.
Результат и Пояснения
С помощью стандартных отклонений вы сможете оценить дисперсию, т.е. размах ваших данных. При работе с нормально распределенными данными в одном измерении, 68%, 95% и 99,7% значений данных будут находиться в пределах одного, двух и трех стандартных отклонений соответственно. Однако при работе с многомерными пространственными данными (переменные x, y и z) эти проценты неверны. Например, при нормальном распределении данных в двух измерениях эллипс одного стандартного отклонения покрывает приблизительно 63% объектов, двух стандартных отклонений – 98% объектов, а трех – 99.9%. Аналогично, для трех измерений проценты будут следующие: 61, 99 и 100.
По этой причине стандартные отклонения масштабируются с помощью уточняющего коэффициента для создания эллипса или эллипсоида, содержащего 68, 95 и 99 процентов объектов для 2D- и 3D-данных (при условии, что данные подчиняются пространственному нормальному распределению). Эти уточняющие коэффициенты для дисперсий (квадраты стандартных отклонений) приведены в следующей таблице:
| Одномерные данные | Двухмерные данные | Трехмерные данные | |
|---|---|---|---|
1 среднеквадратическое отклонение | 1.00 | 1.41 | 1.73 |
2 среднеквадратических отклонения | 2.00 | 2.83 | 3.46 |
3 среднеквадратических отклонения | 3.00 | 4.24 | 5.20 |
Для двухмерных данных инструмент Направленное распределение (Эллипс стандартного отклонения) создает новый класс объектов, содержащий эллиптический полигон с центром в среднем центре всех объектов (или всех комбинаций объектов, если значение указано для параметра Поле комбинаций). Атрибутивные значения для этих выходных эллиптических полигонов включают 2 стандартных расстояния (длинная и короткая оси), ориентацию эллипса и поле комбинаций, если указано. Ориентация представляет собой поворот длинной оси, измеряемой по часовой стрелке. Также можно указать число стандартных отклонений для представления (1, 2 или 3), чтобы охватить различные проценты объектов.
Для трехмерных точечных данных (если для ваших данных включена координата z и имеется 3D-атрибут, например, высота) инструментом создается новый класс объектов, содержащий мультипатч-эллипсоид с центром в среднем центре для всех объектов (либо для всех комбинаций, при использовании поля комбинаций). Значения атрибутов для этих выходных эллипсоидов включают три стандартных расстояния (большая, малая ось и ось высоты), угол, наклон и поворот эллипсоида и, дополнительно, поле комбинаций. Значения угла, наклона и поворота эллипсоида описывают ориентацию эллипсоида в 3D-пространстве. Также можно указать число стандартных отклонений для представления (1, 2 или 3), чтобы охватить различные проценты объектов.
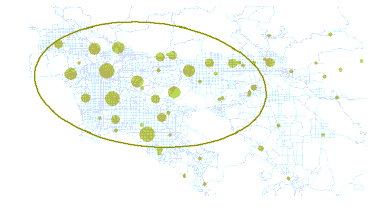
Возможное применение
- Картографирование трендов распределения для набора преступлений может определить взаимосвязь с конкретными физическими процессами (линии с барами и ресторанами, конкретный проспект и т.д.).
- Картографирование подземных колодцев для определенного загрязнителя может быть индикатором распространения токсинов, и соответственно, может быть полезно для принятия смягчающих стратегий.
- Сравнивая размер, форму и перекрытие эллипсов для различных расовых и этнических групп, можно получить дополнительную информацию о расовой или этнической сегрегации.
- Вычерчивание эллипсов для вспышек заболеваний во времени может быть использовано для моделирования его распространения.
- Проверка распределения высот для штормов определенной категории – важный момент для изучения влияния состояния атмосферы на авиационные происшествия.
Дополнительные ресурсы
Chew, Victor. "Точные, прогнозируемые и возможные области для многовариантного нормального распределения." Journal of the American Statistical Association. 61.315 (1966): 605-617. https://doi.org/10.1080/01621459.1966.10480892.
Fisher, N. I., T. Lewis, and B. J. J. Embleton. 1987. "Statistical Analysis of Spherical Data". Первое издание. Cambridge: Cambridge University Press. Cambridge Books Online. Web. 26 April 2016. https://doi.org/10.1017/CBO9780511623059.
Levine, Ned. "CrimeStat III: программа пространственной статистики для анализа мест совершений преступлений (версия 3.0)." Houston (TX): Ned Levine & Associates/Washington, DC: National Institute of Justice (2004). https://doi.org/10.3886/ICPSR02824.v1.
Wang, Bin, Wenzhong Shi, and Zelang Miao. 2015. "Confidence Analysis of Standard Deviational Ellipse and Its Extension into Higher Dimensional Euclidean Space". PLoS ONE. 10(3), e0118537.https://doi.org/10.1371/journal.pone.0118537.