Тема содержит примеры и предполагаемые результаты различных опций параметра Отношение, доступных для инструмента Выбрать в слое по расположению и инструмента Пространственное соединение.
Более подробные сведения об опциях Пересечение 3D и В пределах расстояния 3D см. в разделе Выбрать по расположению: 3D отношения.
Терминология
| Ключевое слово диалогового окна | Ключевое слово Python |
|---|---|
Пересечение | INTERSECT |
Пересечение 3D | INTERSECT_3D |
Пересечение (СУБД) | INTERSECT_DBMS |
В пределах геодезического расстояния | WITHIN_A_DISTANCE_GEODESIC |
В пределах расстояния | WITHIN_A_DISTANCE |
В пределах расстояния 3D | WITHIN_A_DISTANCE_3D |
Содержит | CONTAINS |
Полностью содержит | COMPLETELY_CONTAINS |
Содержит по Клементини | CONTAINS_CLEMENTINI |
Внутри | WITHIN |
Полностью в пределах | COMPLETELY_WITHIN |
Внутри по Клементи | WITHIN_CLEMENTINI |
Идентичны | ARE_IDENTICAL_TO |
Касаются границы | BOUNDARY_TOUCHES |
Имеют общий линейный сегмент с | SHARE_A_LINE_SEGMENT_WITH |
Пересекается границей | CROSSED_BY_THE_OUTLINE_OF |
Имеют центр внутри | HAVE_THEIR_CENTER_IN |
Все имеющиеся описания используют терминологию инструмента Выбрать в слое по расположению. Однако эти детали также применяются к инструменту Пространственное соединение. Имена параметров различаются в инструментах:
- У инструмента Выбрать в слое по расположению имеется параметр Входной векторный слой; эквивалентный параметр для инструмента Пространственное соединение – это Целевые объекты.
- У инструмента Выбрать в слое по расположению имеется параметр Выбирающие объекты; эквивалентный параметр инструмента Пространственное соединение – это Объекты соединения.
- У инструмента Выбрать в слое по расположению имеется параметр Отношение; эквивалентный параметр инструмента Пространственное соединение – это Опции сопоставления.
Пространственные отношения Clementini.
Опции Внутри по Клементини и Содержит по Клементини относятся к внутренней части и содержат пространственные отношения, определенные в следующем документе: Clementini, Eliseo, Paolino Di Felice, and Peter van Oosterom, "A Small Set of Formal Topological Relationships Suitable for End-User Interaction," Proceedings of the Third International Symposium on Advances in Spatial Databases, 277–295, June 23–25, 1993.
Контраст трех содержит пространственные отношения
Для линий граница – это две конечных точки; для полигонов – это ребро.
- Содержит – выбирает объекты во входном векторном слое, которые содержат объект вспомогательного слоя выборки. Выбранные пространственные объекты могут быть как внутри, так и на границе входного векторного слоя.
- Полностью содержит – выбирает объекты во входном векторном слое, которые содержат объект в вспомогательного слоя выборки, до тех пор, пока объект в вспомогательного векторного слоя не пересечет границу входного векторного слоя.
- Содержит по Клементини – результаты идентичны опции Содержит с одним исключением. Если объект вспомогательного слоя выборки полностью находится на границе входного векторного слоя, где ни одна часть содержащегося объекта не находится внутри объекта входного векторного слоя, входной объект не будет выбран. Отношение Клементини устанавливает, что граница точки всегда пустая, а граница линии – конечные точки.
Опции Содержит и Содержит по Клементини производят идентичные результаты с точечными и мультиточечными входными данными, и выбираемыми объектами будут точки и мультиточки.
Контраст трех в рамках пространственных отношений
- Внутри – выбирает объекты во входном векторном слое, которые находятся внутри объектов вспомогательного слоя выборки.
- Полностью внутри – результат работы идентичен опции Внутри с одним исключением. Если объект во входном векторном слое пересекает границу объекта вспомогательного слоя выборки, тогда он не выбирается.
- Внутри по Клементини – результат идентичен опции Внутри за исключением случаев, когда весь объект во входном векторном слое находится на границе объекта вспомогательного слоя выборки. Отношение Клементини устанавливает, что граница точки всегда пустая, а граница линии – конечные точки.
Легенда диаграмм
для всех приведенных ниже примеров применяется следующая легенда:
- Входной объект - зеленый круг
- Центр входного объекта - красный X
- Выбирающий объект - серый квадрат
Диаграммы подписаны A, B, C и т. д. Каждая опция отношения (Пересекает, Содержит и т. д.), действительное для комбинации геометрий, находится в списке в левом столбце таблицы. Геометрические случаи, которые будут выбраны для этого отношения, перечислены в правом столбце таблицы.
Выбрать точки, используя точки
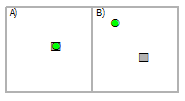
Пересечение | A |
Пересечение (СУБД) | A |
Содержит | A |
Содержит по Клементини | A |
Внутри | A |
Внутри по Клементи | A |
Идентичны | A |
Имеют центр внутри | A |
Выбрать точки, используя мультиточки
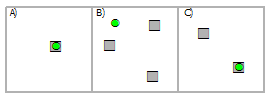
Пересечение | A, C |
Пересечение (СУБД) | A, C |
Содержит | A |
Содержит по Клементини | A |
Внутри | A, C |
Внутри по Клементи | A, C |
Идентичны | A |
Имеют центр внутри | A, C |
Выбрать точки, используя линии
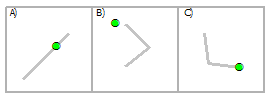
Пересечение | A, C |
Пересечение (СУБД) | A, C |
Внутри | A, C |
Полностью в пределах | A |
Внутри по Клементи | A |
Имеют центр внутри | A, C |
Касаются границы | C |
Выбрать точки, используя полигоны
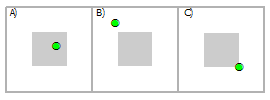
Пересечение | A, C |
Пересечение (СУБД) | A, C |
Внутри | A, C |
Полностью в пределах | A |
Внутри по Клементи | A |
Имеют центр внутри | A, C |
Касаются границы | C |
Выбрать мультиточки, используя точки
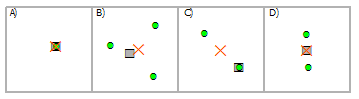
Пересечение | A, C |
Пересечение (СУБД) | A, C |
Содержит | A, C |
Содержит по Клементини | A, C |
Внутри | A |
Внутри по Клементи | A |
Идентичны | A |
Имеют центр внутри | A, D |
Выбрать мультиточки, используя мультиточки
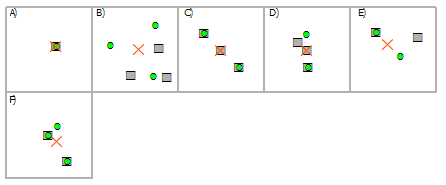
Пересечение | A, C, D, E, F |
Пересечение (СУБД) | A, C, D, E, F |
Содержит | A, F |
Содержит по Клементини | A, F |
Внутри | A, C |
Внутри по Клементи | A, C |
Идентичны | A |
Имеют центр внутри | A, D |
Выбрать мультиточки, используя линии
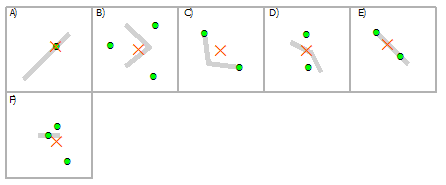
Пересечение | A, C, E, F |
Пересечение (СУБД) | A, C, E, F |
Внутри | A, C, E |
Полностью в пределах | A |
Внутри по Клементи | A, E |
Имеют центр внутри | A, D, E |
Касаются границы | C, E |
Выбрать мультиточки, используя полигоны
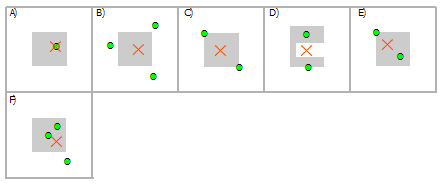
Пересечение | A, C, D, E, F |
Пересечение (СУБД) | A, C, D, E, F |
Внутри | A, C, D, E |
Полностью в пределах | A |
Внутри по Клементи | A, D, E |
Имеют центр внутри | A, B, C, E, F |
Касаются границы | C, E |
Выбрать линии, используя точки
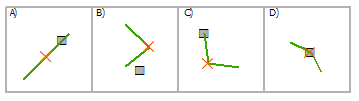
Пересечение | A, C, D |
Пересечение (СУБД) | A, C, D |
Содержит | A, C, D |
Полностью содержит | A, D |
Содержит по Клементини | A, D |
Имеют центр внутри | D |
Касаются границы | C |
Выбрать линии, используя мультиточки
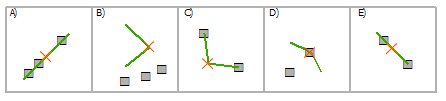
Пересечение | A, C, D, E |
Пересечение (СУБД) | A, C, D, E |
Содержит | A, C, E |
Полностью содержит | A |
Содержит по Клементини | A, E |
Имеют центр внутри | D |
Касаются границы | C, E |
Выбрать линии, используя линии
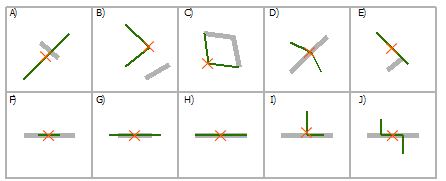
Пересечение | A, C, D, E, F, G, H, I, J |
Пересечение (СУБД) | A, C, D, E, F, G, H, I, J |
Содержит | G, H |
Полностью содержит | G |
Содержит по Клементини | G, H |
Внутри | F, H |
Полностью в пределах | F |
Внутри по Клементи | F, H |
Идентичны | H |
Касаются границы | C, E |
Имеют общий линейный сегмент с | F, G, H, I, J |
Выбрать линии, используя полигоны
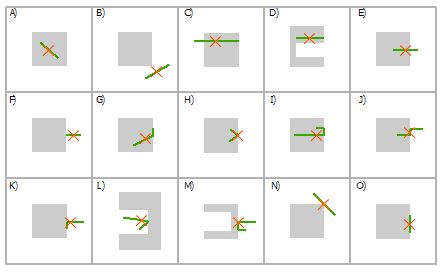
Пересечение | A, C, D, E, F, G, H, I, J, K, L, M, N, O |
Пересечение (СУБД) | A, C, D, E, F, G, H, I, J, K, L, M, N, O |
Внутри | A, D, G, H, I, O |
Полностью в пределах | A |
Внутри по Клементи | A, D, G, H, I |
Касаются границы | F, G, H, I, K, L, M, N, O |
Имеют общий линейный сегмент с | G, I, J, K, M, O |
Пересекается границей | C, E, H, L, N |
Имеют центр внутри | A, C, D, E, G, H, I, J, O |
Выбрать полигоны, используя точки
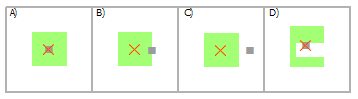
Пересечение | A, B |
Пересечение (СУБД) | A, B |
Содержит | A, B |
Полностью содержит | A |
Содержит по Клементини | A |
Имеют центр внутри | A, D |
Касаются границы | B |
Выбрать полигоны, используя мультиточки
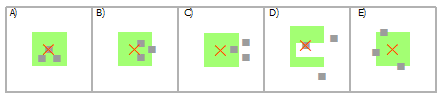
Пересечение | A, B, C, E |
Пересечение (СУБД) | A, B, C, E |
Содержит | A, B, E |
Полностью содержит | A |
Содержит по Клементини | A, B |
Имеют центр внутри | A, D |
Касаются границы | E |
Выбрать полигоны, используя линии
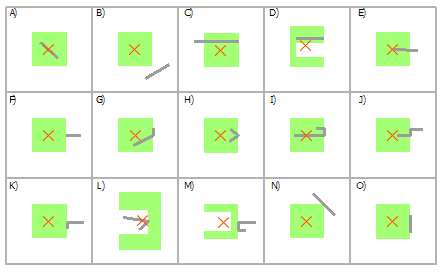
Пересечение | A, C, D, E, F, G, H, I, J, K, L, M, N, O |
Пересечение (СУБД) | A, C, D, E, F, G, H, I, J, K, L, M, N, O |
Содержит | A, D, G, H, I, O |
Полностью содержит | A |
Содержит по Клементини | A, D, G, H, I |
Касаются границы | F, G, H, I, K, L, M, N, O |
Имеют общий линейный сегмент с | G, I, J, K, M, O |
Пересекается границей | C, E, H, L, N |
Имеют центр внутри | E, I, L |
Выбрать полигоны, используя полигоны
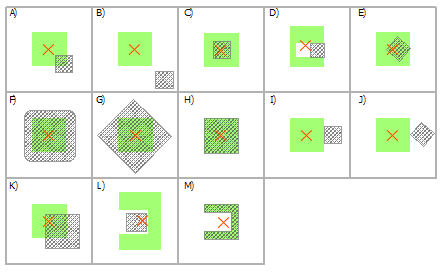
Пересечение | A, C, D, E, F, G, H, I, J, K, M |
Пересечение (СУБД) | A, C, D, E, F, G, H, I, J, K, M |
Содержит | C, E, H, M |
Полностью содержит | C |
Содержит по Клементини | C, E, H, M |
Внутри | F, G, H, M |
Полностью в пределах | F |
Внутри по Клементи | F, G, H, M |
Идентичны | H, M |
Касаются границы | D, E, G, H, I, J, M |
Имеют общий линейный сегмент с | D, H, I, M |
Пересекается границей | A, E, G, J, K |
Имеют центр внутри | C, E, F, G, H, K, L |