Как работает инструмент Тренд

Доступно с лицензией Spatial Analyst.

Доступно с лицензией 3D Analyst.

Тренд – глобальная полиномная интерполяция, соответствующая ровной поверхности, определенной математической функцией (полиномом) для входных точек образца. Поверхность тренда постепенно изменяется и охватывает шаблоны грубых масштабов в данных.

Основы алгоритма

Концептуально, интерполяция по методу тренда сходна с установкой листа бумаги между поднятыми точками (поднятыми до высоты значения). Это показано на диаграмме ниже для набора точек образца высот, взятых на холме с небольшим уклоном. Лист бумаги пурпурный.

иллюстрация плоской поверхности тренда

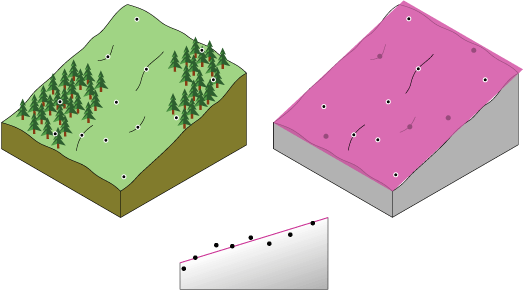
Плоский лист бумаги не будет точно охватывать ландшафт, содержащий долину. Однако, если вы согнете лист бумаги один раз, вы получите гораздо лучшее соответствие. Добавление члена в математическую формулу дает аналогичный результат, сгиб плоскости. Плоская поверхность (нет сгиба на листе бумаги) – это полином первого порядка (линейный). Допустим, что один перегиб – это полином второго порядка (квадратический), два перегиба – полином третьего порядка (кубический) и т. д. Этот инструмент может работать максимум с 12 перегибами (12 порядками). На следующем рисунке концептуально показан полином второго порядка, соответствующий долине.

иллюстрация искривленной поверхности тренда

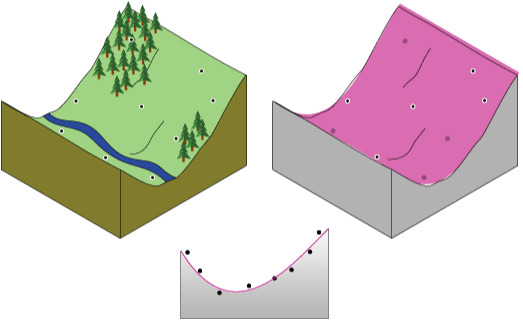
Редко лист бумаги проходят через фактически измеренные точки, таким образом делая интерполяцию по методу тренда неточным методом интерполяции. Некоторые точки будут расположены выше листа бумаги, другие – ниже. Однако, если вы добавите высоту до высоты точек выше листа бумаги, а также добавите высоту для точек ниже листа бумаги, эти две суммы должны быть равны. Поверхность, данная пурпурным цветом, получается путём использования подходящей регрессии наименьших квадратов. Результирующая поверхность сводит к минимуму различия между квадратами поднятых значений и листом бумаги.

Чем меньше среднеквадратическая (RMS) ошибка, тем точнее интерполированная поверхность представляет входные точки. Наиболее распространенными порядками полиномов являются один через три. Интерполяция поверхности по методу тренда строит сглаженные поверхности.

Когда используется интерполяция по методу тренда

Интерполяция по методу тренда приводит к сглаженной поверхности, которая представляет постепенные тренды поверхности в исследуемой области. Этот тип интерполяции может использоваться для:

• Подгонки поверхности к точкам образца, если поверхность варьируется постепенно от участка к участку исследуемой области, например, загрязнение окружающей среды в промышленной зоне.
• Исследования или удаления эффектов трендов с большим диапазоном или глобальных трендов. При таких обстоятельствах, метод часто называют анализ поверхности тренда.

Интерполяция по методу тренда создаёт постепенно изменяющуюся поверхность с помощью полиномов низкого порядка, которые описывают физический процесс, например, загрязнение и направление ветра. Однако, чем более сложный полином, тем труднее приписать ему физический смысл. Кроме того, вычисленные поверхности весьма чувствительны к выпадающим значениям (чрезвычайно высоким и низким значениям), особенно на ребрах.

Типы интерполяции по методу тренда

Существует два основных типа интерполяции по методу Тренда: линейная и логарифмическая.

Линейный тренд

Интерполятор поверхности по методу Линейного тренда создает растр из значений с плавающей точкой. Он использует полиномиальное уравнение регрессии для подбора для входных точек поверхности, определяемой с использованием метода наименьших квадратов. Этот метод позволяет управлять порядком полинома, используемого для подбора поверхности. Для понимания этого метода, рассмотрим полином первого порядка. Интерполяция поверхности по методу линейного тренда первого порядка выполняет для набора входных точек подбор плоскости, определяемой на основе метода наименьших квадратов.

Интерполяция поверхности по методу тренда строит сглаженные поверхности. Построенная поверхность редко проходит через исходные опорные точки, поскольку она выполняет подбор лучшей поверхности для всего набора опорных точек. Когда применяется порядок полинома выше единицы, интерполятор может строить растр, минимальное и максимальное значения которого превышают минимальное и максимальное значения входного файла пространственных данных.

Логарифмический тренд

Опция Логистический, используемая для построения поверхности тренда, хорошо подходит для прогнозирования присутствия или отсутствия определенного явления (в форме вероятности) для заданного набора точек (x,y) в пространстве. Z-значение – это категоризированная случайная переменная с только двумя возможными результатами – например, наличие вымирающих видов или отсутствие таких видов. Эти два z-значения могут быть кодированы единицей и нулем, соответственно. Эта опция создает непрерывный грид вероятности с значениями ячеек от нуля до единицы.

Для вычисления нелинейной модели поверхности вероятности без предварительного преобразования модели в линейную форму используется оценка по методу максимального подобия.

Выходной файл RMS

Файл ошибки RMS содержит среднеквадратическую ошибку интерполяции, полученную путем сравнения значений в местоположениях во входном наборе данных с значениями в тех же самых местоположениях на проинтерполированной растровой поверхности.

Ошибка RMS может использоваться для определения наилучшего значения, которое будет применено для параметра порядка {order} интерполяции после последовательного изменения значения порядка до тех пор, пока вы не получите наименьшее значение ошибки (RMS). В отчёт включается также значение хи-квадрата.

Пример

Пример выходного файла RMS из инструмента Тренд с Полиномом 3-го порядка:

coef #          coef
------ ----------------
     0 -1192066.7888371
     1 -1.78479492586755
     2 -0.195982103615487
     3 -8.87072249743903e-1
     4 -2.0538267625596e-1
     5 -3.85610088343239e-1
     6 -1.46420255709888e-2
     7 -5.31539027745154e-2
     8 -2.59261094879031e-3
     9 9.71651459136166e-4
------ ----------------
RMS Error  = 296.957857221845
Chi-Square  = 17019506.0103975

Интерполируемое значение в любом месте выходного растра для тренда третьего порядка может быть определено с помощью сложения значений, полученных из серии уравнений. Для этих уравнений, x = долгота местоположения, y = широта, а c_n – коэффициент из предыдущей таблицы. Уравнения для вычисления интерполяции третьего порядка:

Prediction(x,y) = c0 + 
                  x·c1 + y·c2 + 
                  x2·c3 + x·y·c4 + y2·c5 +
                  x3·c6 + x2·y·c7 + x·y2·c8 + y3·c9

Естественно, коэффициент 0 всегда является пересечением. Отсюда начинается итерация в терминах первого порядка, начиная с самых высоких значений x и заканчивающаяся без значений x. Затем происходит переход к терминам второго порядка и повторная итерация значений x по убыванию, то же повторяется для третьего порядка.

Примечание:

При увеличении порядка уравнения применяются те же способом. Например, если выбран четвертый порядок, в таблице RMS будут указаны еще пять значений (коэффициенты 10, 11, 12, 13 и 14), число уравнений, использующих их, увеличится пропорционально.