Нечеткое множество (Spatial Analyst)

Доступно с лицензией Spatial Analyst.

Краткая информация

Трансформирует входной растр по шкале от 0 до 1, указывая полноту принадлежности в наборе на основе заданного алгоритма подготовки задачи для решения методами нечеткой логики.

Значение 1 означает полную принадлежность к нечеткому множеству, с уменьшающейся принадлежностью до 0, что указывает на то, что значение не принадлежит к нечеткому множеству.

Более подробно о том, как работает инструмент Нечеткое множество

Использование

• Этот инструмент не трансформирует категорийные данные. Чтобы включить категорийные данные в анализ нечеткого наложения, необходима предварительная обработка ячеек. Вы можете создать модель или запустить следующие инструменты геообработки. Сначала используйте инструмент Переклассификация, чтобы предоставить новый диапазон значений (например, 1 к 100). Затем Разделите результат на коэффициент (например, на 100), чтобы нормализовать выходные значения от 0,0 до 1,0.

• Спред определяет, насколько быстро значения нечеткого множества уменьшаются от 1 до 0. Чем больше значение, тем больше нечеткости у средней точки. Говоря другими словами, при уменьшении значения распределения, значения принадлежности к нечеткому достигают 0 медленнее. Выборка соответствующего значения распределения – это субъективный процесс, который зависит от диапазона четких значений. Для опции Гауссов или Ближайший можно начать со значения по умолчанию, равного 0,1. Как правило, значения варьируются в диапазоне [0,01–1] или [0,001-1], соответственно. Для опций Маленький и Большой, можно начать со значения по умолчанию, равного 5, и значения, как правило, варьируются от 1 до 10.

  

  Влияние разброса на на Гауссовом нечетком множестве.

• Это может быть тем случаем, когда ни у одного входного значения не будет 100 процентной возможности быть членом указанного набора. Другими словами, ни одно входное значение не имеет нечеткого множества 1. В такой ситуации вы можете масштабировать значения нечеткого множества для получения нового масштаба. Например, если наибольшее значение принадлежности для входных значений – 0,75, то вы можете установить новый масштаб, умножая каждое нечеткое множество на 0,75.

• Применяемые ограничения: Очень и Несколько. Очень также известен как концентрация, определенная как функция нечеткого множества в квадрате. Несколько также называется растяжение или Более или Менее. Это квадратный корень функции нечеткого множества. Очень и Несколько увеличивают и уменьшают, соответственно, функции нечеткого множества соответственно.

• Отрицательные значения неприемлемы для функций нечеткого множества Маленький и Большой.

• Для функции нечеткого множества Линейный входной растр должен быть упорядоченными данными. Минимум может быть меньше максимума для создания положительного уклона, или больше максимума для создания отрицательного уклона для трансформации.

  Если минимум меньше максимума, для трансформации используется функция с положительным уклоном; если минимум больше максимума, используется функция с отрицательным уклоном.

• См. раздел Среда анализа и Spatial Analyst для получения дополнительной информации о среде геообработки данного инструмента.

Параметры

Диалог

Подпись	Описание	Тип данных
Входной растр	Входной растр, значения которого будут переклассифицированы по шкале от 0 до 1. Тип растра может быть целочисленным или с плавающей точкой.	Raster Layer
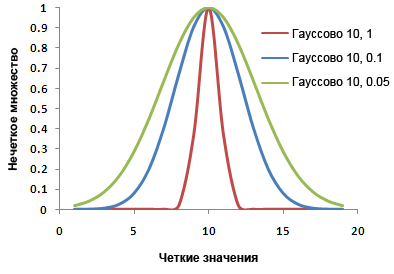
Тип принадлежности (Дополнительный)	Задает алгоритм, используемый в подготовке задачи для решения методами нечеткой логики для входного растра. Определенные настройки для Типа принадлежностей применяют параметры Распределения для того чтобы определить насколько быстро значения нечеткого множество уменьшаются от 1 до 0. Значения спреда по умолчанию перечислены в расположенной ниже таблице. Gaussian—Присваивается значение принадлежности равное 1 в средней точке.Принадлежность уменьшается до 0 для значений, которые отклоняются от средней точки в соответствии с нормальной кривой. Кривая Гаусса аналогична функции Ближайший объект, но имеет более узкое распределение. Средняя точка является по умолчанию средней точкой диапазона значений входного растра. Распределение – Значение по умолчанию – 0,1. Обычно, значения изменяются в пределах [0,01–1]. Small—Используются для указания того, что небольшие значения входного растра имеют большие значения принадлежности в нечетком множестве.Присваивается значение принадлежности равное 0,5 в средней точке. Средняя точка является по умолчанию средней точкой диапазона значений входного растра. Распределение — Значение по умолчанию – 5. Large—Используются для указания того, что большие значения входного растра имеют высокий уровень принадлежности к нечеткому множеству.Присваивается значение принадлежности равное 0,5 в средней точке. Средняя точка является по умолчанию средней точкой диапазона значений входного растра. Распределение — Значение по умолчанию – 5. Near—Рассчитывает принадлежность для значений, которые близки к промежуточным.Присваивается значение принадлежности равное 1 в средней точке. Принадлежность уменьшается до 0 для значений, которые отклоняются от средней точки. Средняя точка является по умолчанию средней точкой диапазона значений входного растра. Распределение – Значение по умолчанию – 0,1. Как правило, значения варьируются в диапазоне [0,001–1]. MSLarge—Рассчитывает множество, которое основано на среднем и стандартном отклонении входных данных, где большие значения имеют большие значения принадлежности.Результат может быть похож на функцию Большие, в зависимости от определенного среднего значения и стандартного отклонения. Средний множитель – по умолчанию, равен 1. Стандартный множитель отклонения – по умолчанию, равен 2. MSSmall—Рассчитывает множество, которое основано на среднем и стандартном отклонении входных данных, где небольшие значения имеют большие значения принадлежности. Этот тип членства используется по умолчанию.Результат может быть похож на функцию Небольшие в зависимости от определенного среднего значения и стандартного отклонения. Средний множитель – по умолчанию, равен 1. Стандартный множитель отклонения – по умолчанию, равен 2. Linear—Рассчитывает множество, которое основано на линейном преобразовании входного растра.Присваивается значение принадлежности, равное 0 для минимума и множество, равное 1, для максимума. Минимум – по умолчанию равен 1. Максимум – по умолчанию равен 2.	Fuzzy function
Ограничение (Дополнительный)	Задание ограничений увеличивает или уменьшает значения принадлежности, которые изменяют значения нечеткого множества. Применяемые защиты используются для того, чтобы оказать помощь в управлении критериями или важными атрибутами. Нет—Ограничения не применяются. Это значение по умолчанию Somewhat—Растяжение определяется как квадратный корень функции нечеткого множества Ограничение увеличивает функции нечеткого множества. Очень—Также известен как концентрация, определенная как функция нечеткого множества в квадрате. Ограничение уменьшает функции нечеткого множества.	String

Возвращаемое значение

Подпись	Описание	Тип данных
Выходной растр	Выходными данными будет растр со значениями с плавающей точкой в диапазоне от 0 до 1.	Raster

Python

FuzzyMembership(in_raster, {fuzzy_function}, {hedge})

Имя	Описание	Тип данных
in_raster	Входной растр, значения которого будут переклассифицированы по шкале от 0 до 1. Тип растра может быть целочисленным или с плавающей точкой.	Raster Layer
fuzzy_function (Дополнительный)	Задает алгоритм, используемый в подготовке задачи для решения методами нечеткой логики для входного растра. Нечеткие классы используются для определения типа принадлежности. Типы классов принадлежности: FuzzyGaussian, FuzzyLarge, FuzzyLinear, FuzzyMSLarge, FuzzyMSSmall, FuzzyNear, and FuzzySmall. Ниже представлены формы классов принадлежности: FuzzyGaussian({midpoint},{spread}) FuzzyLarge({midpoint},{spread}) FuzzyLinear({minimum},{maximum}) FuzzyMSLarge({meanMultiplier},{STDMultiplier}) FuzzyMSSmall({meanMultiplier},{STDMultiplier}) FuzzyNear({midpoint},{spread}) FuzzySmall({midpoint},{spread})	Fuzzy function
hedge (Дополнительный)	Задание ограничений увеличивает или уменьшает значения принадлежности, которые изменяют значения нечеткого множества. Применяемые защиты используются для того, чтобы оказать помощь в управлении критериями или важными атрибутами. NONE—Ограничения не применяются. Это значение по умолчанию SOMEWHAT—Растяжение определяется как квадратный корень функции нечеткого множества Ограничение увеличивает функции нечеткого множества. VERY—Также известен как концентрация, определенная как функция нечеткого множества в квадрате. Ограничение уменьшает функции нечеткого множества.	String

Возвращаемое значение

Имя	Описание	Тип данных
out_raster	Выходными данными будет растр со значениями с плавающей точкой в диапазоне от 0 до 1.	Raster

Пример кода

FuzzyMembership, пример 1 (окно Python)

Этот пример создает растр принадлежности, с помощью функцию Гауссова (Gaussian), где у значений высот близких к средней точке (1,200 футов) выше значения принадлежности.

import arcpy
from arcpy.sa import *
from arcpy import env
env.workspace = "c:/sapyexamples/data"
outFzyMember = FuzzyMembership("elevation", FuzzyGaussian(1200, 0.06))
outFzyMember.save("c:/sapyexamples/fzymemb")

FuzzyMembership, пример 2 (автономный скрипт)

В этом примере создается растр нечеткого множества, с помощью функции Гаусса (Gaussian), где у значений высот близких к средней точке (1,200 футов) значения принадлежности выше.

# Name: FuzzyMembership_Ex_02.py
# Description: Scales input raster data into values ranging from zero to one
#     indicating the strength of a membership in a set. 
# Requirements: Spatial Analyst Extension

# Import system modules
import arcpy
from arcpy import env
from arcpy.sa import *

# Set environment settings
env.workspace = "C:/sapyexamples/data"

# Set local variables
inRaster = "elevation"

# Create the FuzzyGaussian algorithm object
midpoint = 1000
spread = 0.4
myFuzzyAlgorithm = FuzzyGaussian(midpoint, spread)

# Execute FuzzyMembership
outFuzzyMember = FuzzyMembership(inRaster, myFuzzyAlgorithm)

# Save the output
outFuzzyMember.save("c:/sapyexamples/fzymemb2")

Параметры среды

Автоматическое подтверждение, Размер ячейки, Метод проецирования размера ячейки, Текущая рабочая область, Экстент, Географические преобразования, Маска, Выходное ключевое слово CONFIG, Выходная система координат, Временная рабочая область, Растр привязки, Размер листа