多くの GIS 分析ワークフローで重要な構成要素は、分析範囲で 2 変数を比較し、それらの変数に関係があるか、またどのような関係があるかを判断することです。 たとえば、特定の地域において、糖尿病と肥満の間に関係があるでしょうか? 歴史的に、このような種類の質問の答えは、カートグラフィの注意深い比較、または線形回帰分析で求めていました。 カートグラフィの比較は主観的な可能性があり、回帰分析は単純な関係のみを検出できます。
[ローカル 2 変数リレーションシップ (Local Bivariate Relationships)] ツールでは、一方の変数値が他方の変数値に従属しているか、つまり影響を受けているかどうかと、これらの関係が地理的空間にわたって変化しているかを判定することにより、同一マップ上の 2 変数の関係を定量化できます。 このツールは、個々の局所近傍において、2 変数の共有する情報量を定量化するエントロピー統計値を計算します。 多くの場合に線形関係のみを捕捉できる他の統計値 (線形回帰など) とは異なり、エントロピーは 2 変数の構造的な関係を捕捉できます。指数関数、2 次関数、正弦関数、さらに一般的な数学関数では表すことのできない複雑な関係を捕捉できます。 このツールは多角形またはポイントを受け入れ、各入力フィーチャの関係の有意性と形式を集計した出力フィーチャクラスを作成します。 さらに、カスタム ポップアップおよびさまざまな診断、チャート、およびメッセージが用意されています。
適用例
このツールは次のような用途で使用できます。
- CDC (米国疾病管理予防センター) では、「肥満の人たちは、正常つまり健康的な体重の人たちと比較して、2 型糖尿病を含む多くの重篤な疾病および健康状態になるリスクが高くなります」と述べています。 CDC がこのツールを使用すれば、肥満と糖尿病の関係の強さを定量化し、関係が分析範囲にわたって一貫しているかどうかを調べることができます。
- 公共衛生機関は、大気汚染レベルと社会経済的な要因との関係を調べて、環境に対する潜在的な不正を見つけ出すことができます。
エントロピー法
2 変数が相互に関係していることは、どのような意味がありますか? 変数の関係には多くの種類がありますが、最も単純な考え方では、一方の変数値を観察することにより他方の変数の情報を学習できる場合、この 2 変数には関係があります。 たとえば、肥満に関する情報を観察することにより、糖尿病に関する情報を得ることができます。 これは 2 変数が従属関係にあることを示し、反対に一方の変数を観察しても他方の変数に関する情報が得られない場合、変数は独立しています。
変数の関係の度合いを測定する方法の 1 つがエントロピーを使用する方法です。 エントロピーは情報理論の基本的な概念であり、確率変数の不確かさの程度を定量化するために使用されます。 一般的に、変数が予測しにくいほど、エントロピーが高くなります。 エントロピーは幅広く適用可能で、個々の確率変数について計算できます。また、2 つ以上の変数の結合エントロピーを計算できます。 2 変数の結合エントロピーは、2 変数のエントロピーの和から 2 変数の相互情報量を減算した値に等しくなります。 相互情報量は、変数間の従属レベルの便利な定量として使用されます。一方の変数値を観察することで他方の変数について得られる情報量がどれだけあるかを直接測定するためです。
相互情報量を推定するには、個々の変数のエントロピーと、その結合エントロピーをすべて推定する必要があります。 ただし、これらの値は基になっている変数の分布に依存し、実際にはほとんどわかりません。 幸い、最近の研究で、べき乗の重み付き最小スパニング ツリーを変数の結合分布の代わりに使用して、複数の変数の結合エントロピーを推定できることが示されました (Guo、2010)。 これにより、2 変数の個々の分布が不明でも、結合エントロピーを推定できます。 結合エントロピーを推定できることは便利ですが、実際には、2 変数に関係があるかどうかを調べるには変数間の相互情報量を知る必要があります。 2 変数の分布が不明な場合は相互情報量を直接推定できませんが、順列を使用して、統計的に有意な関係の帰無仮説検定を作成できます。
順列を使用した有意な関係の検定
前のセクションで示したように、2 変数に関係があるかどうかという質問は、2 変数の結合エントロピー (推定可能) が 2 変数の個々のエントロピーの合計 (推定不可) より有意に小さいかどうかをたずねることと同じです。 言い換えると、データの結合エントロピーが、2 変数が独立の場合と比べて有意に低くなるか、という質問です。
この判定を行うために、1 番目の変数の個々の値を 2 番目の変数の新しい値にランダムに再び代入して、変数の順列を行います。 ペアの組み合わせをランダムに行うことにより、順列後のデータセットは相互情報を共有しなくなりますが、2 変数の個々のエントロピーは変化しません。 多数の順列データセットを生成し、それらの結合エントロピーを個別に推定することにより、2 変数は独立で無関係であるという帰無仮説の下で結合エントロピーの分布を作成できます。 これにより、実際のデータから推定した結合エントロピーをこの分布と比較できます。また、実際のデータよりも低い結合エントロピーを持つ順列の割合に基づいて、疑似 p 値を計算できます。
局所空間での関係の検定
前述した 2 変数の有意な関係のテストは、任意の連続する 2 変数データに適用できます。 これを局所空間での関係の検定に変更するには、近傍を使用して各入力フィーチャについてこの仮説検定を実行します。 これにより、結果をマッピングして、変数が有意の関係を持つ局所領域を特定できます。
まず、[従属変数] および [説明変数] パラメーターのすべての値が 0 ~ 1 の範囲内にリスケールされます。これは、データセット全体の最小値を減算し、データセット全体の範囲 (最大 - 最小) で除算することで実行されます。 次に、各入力フィーチャについて、次の手順を実行します。
- 近傍のフィーチャを見つけます。 [近傍数] パラメーターは、使用する近傍の数を指定します。 入力フィーチャ自体も近傍としてカウントされます。
- 近傍の 2 つのリスケールされた変数の値をマージして、単一のデータセットを作成します。
- 最小スパニング ツリーを作成し、結合エントロピーを推定します。
- 2 変数の値をランダムに順列して、個々の順列について結合エントロピーを推定します。 [順列の数] パラメーターは、実行する順列の回数を指定します。
- 疑似 p 値を計算し、変数が統計的に有意な関係を持つかどうかを判定します。
この手順では個々の入力フィーチャについて異なる仮説検定を実行するため、[FDR 補正の適用] パラメーターを使用してフォールス ポジティブの結果 (タイプ 1 のエラー) の割合を制御できます。
局所での関係の分類
2 変数が統計的に有意な関係を持つ領域を特定することは非常に重要です。 この情報を使用するために、説明変数が従属変数の値をどの程度まで正確に推定できるかに応じて、変数の関係のタイプを特定できると便利です。
各フィーチャは、次の関係のタイプのいずれかに分類されます。
- [有意でない] - 変数間の関係は統計的に有意ではありません。
- [正の線形] - 説明変数が増加するに伴い、従属変数が線形に増加します。
- [負の線形] - 説明変数が増加するに伴い、従属変数が線形に減少します。
- [凹面] - 説明変数が増加するに伴い、従属変数が凹状曲線に沿って変化します。 一般的に、凹状曲線は下向きに曲がります。
- [凸面] - 説明変数が増加するに伴い、従属変数が凸状曲線に沿って変化します。 一般的に、凸状曲線は上向きに曲がります。
- [未定義の複素数] - 変数に有意な関係がありますが、関係のタイプをその他すべてのカテゴリのいずれでも高い信頼性で説明できません。
次の図に、[凹面] の関係の例を示します。

次の図に、[凸面] の関係の例を示します。

次の手順を使用して、重要な各フィーチャを分類します。
- 説明変数に基づいて従属変数を予測する一般的な線形回帰モデルを推定し、モデルの AICc (修正赤池情報量基準) を計算します。
- 説明変数、および説明変数の 2 乗に基づいて従属変数を予測する 2 番目の線形回帰モデル (2 次回帰モデル) を推定し、AICc を計算します。
- 2 つの回帰モデルの AICc 値を比較し、関係をよりよく表しているモデルを選択します。 2 次モデルが選択されるためには、2 次回帰モデルの AICc が線形回帰モデルの AICc より少なくとも 3 少ない値である必要があります。 それ以外の場合は、線形モデルが選択されます。
- 選択されたモデルの補正 R2 値を計算します。 この値が 0.05 未満の場合、選択したモデルが説明するデータの変化は 5% 未満であり、関係は [未定義の複素数] として分類されます。
- 補正 R2 が 0.05 より大きい場合、次のルールに従って分類します。
- 線形モデルを選択し、係数が正の場合は [正の線形] として分類します。
- 線形モデルを選択し、係数が負の場合は [負の線形] として分類します。
- 2 次モデルを選択し、2 乗項の係数が正の場合は [凸面] として分類します。
- 2 次モデルを選択し、2 乗項の係数が負の場合は [凹面] として分類されます。
結果の解析
このツールの出力は関係のタイプでシンボル化されたフィーチャクラスであり、要約統計量とともにジオプロセシング メッセージに出力されます。 出力フィーチャには、散布図を使用して関係を視覚化するポップアップのほか、情報フィールドが含まれます。
散布図ポップアップ
指定した場合、出力フィーチャごとにカスタムの散布図ポップアップが生成され、マップ上のフィーチャをクリックして表示できます。 次の図は、正の線形関係を持つフィーチャの散布図ポップアップを示しています。
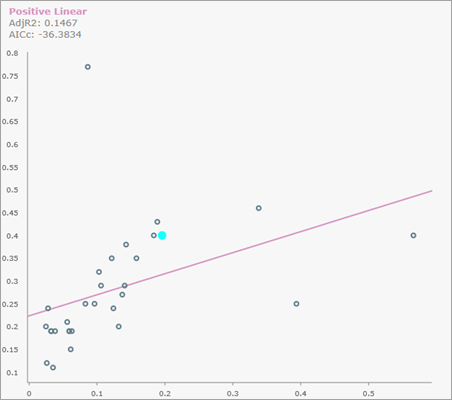
リスケールされた説明変数が x 軸に表示され、リスケールされた従属変数が y 軸に表示されます。 散布図でハイライト表示された 1 つのポイントが実際のフィーチャのポイントであり、その他すべてのポイントはそのフィーチャの近傍のポイントです。
散布図上のポイントの上にポインターを合わせると、フィーチャの [ソース ID] を確認できます。また、リスケールされた従属変数と説明変数の値、およびその未加工 (元のスケール) 値が括弧内に表示されます。
ジオプロセシング メッセージ
統計的な有意性と関係のタイプに関するサマリー情報が、ジオプロセシング メッセージとして表示されます。 これらのメッセージの例を以下に示します。
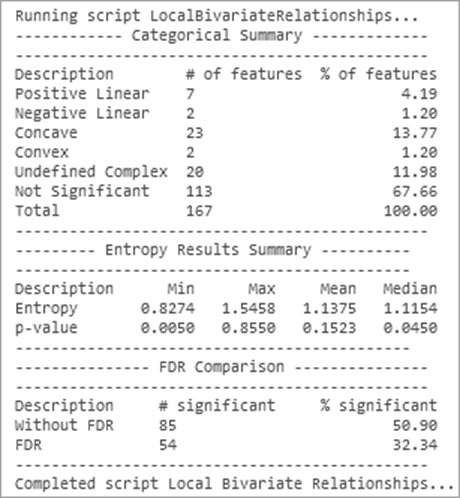
メッセージの [カテゴリ別のサマリー] セクションには、各関係タイプのフィーチャ数と割合がリストされます。 [エントロピー結果のサマリー] セクションには、入力フィーチャのエントロピーと p 値の最小値 (Min)、最大値 (Max)、平均値 (Mean)、および中央値 (Median) がリストされます。 [FDR 比較] セクションには、FDR (False Discover Rate) 補正を適用した場合と適用しない場合の、統計的に有意な関係の数と割合がリストされます。
注意:
ジオプロセシング メッセージは、ツールの実行中に [ジオプロセシング] ウィンドウの下部に表示されます。 ジオプロセシング履歴を使用してこのメッセージにアクセスするには、進行状況バーにポインターを合わせるか、ポップアップ ボタン  をクリックするか、[ジオプロセシング] ウィンドウのメッセージ セクションを展開します。
をクリックするか、[ジオプロセシング] ウィンドウのメッセージ セクションを展開します。
出力フィールド
ツールの出力には、各フィーチャがその関係タイプに分類された方法と理由に関する情報が設定されたさまざまなフィールドが含まれています。
関係の有意性
以下のフィールドには、従属変数と説明変数の関係が統計的に有意であるかどうかに関する情報が設定されます。
- Entropy- フィーチャの推定エントロピー値。
- P-values- 従属変数と説明変数の関係の有意性をテストする疑似 p 値。 この値は、FDR (False Discover Rate) 用には調整されていません。
- Local Bivariate Relationship Confidence Level- フィーチャによって満たされる最高レベルの信頼度。 このフィールドに格納される可能性がある値は、[90% の信頼度]、[95% の信頼度]、[99% の信頼度]、および [有意でない] です。 [FDR (False Discovery Rate) 補正の適用] パラメーター値が指定されている場合、信頼度は FDR (False Discovery Rate) に合わせて調整されます。
関係の分類
以下のフィールドには、従属変数と説明変数の関係タイプの分類に関する情報が設定されます。
- Type of Relationship- 従属変数と説明変数の関係タイプ
- AICc (Linear)- 補正された線形モデルの赤池情報量規準
- R-squared (Linear)- 線形モデルの R2 値
- AICc (Polynomial)- 多項式モデルで補正された赤池情報量規準
- R-squared (Polynomial)- 多項式モデルの R2 値
注意:
AICc および R2 値は、従属変数と説明変数の間に統計的に有意な関係がないフィーチャでは、NULL になります。
回帰係数と有意性
以下のフィールドには、関係の分類に使用される線形モデルと多項式モデルの係数に関する情報が設定されます。
- Intercept- 線形モデルの切片。
- Coefficient (Linear)- 線形モデルの線形項の係数。
- Polynomial Intercept- 多項式モデルの切片。
- Polynomial Coefficient (Linear)- 多項式モデルの線形項の係数。
- Polynomial Intercept (Squared)- 多項式モデルの 2 乗項の係数。
- Significance of Coefficients (Linear)- 切片と係数が 90% の信頼度で統計的に有意であるかどうかを示す 2 文字のコード。 アンダースコア (_) は値が統計的に有意でないことを示し、アスタリスク (*) は値が統計的に有意であることを示します。 たとえば、*_ は切片が統計的に有意であるが、線形係数は有意でないことを示しています。 同様に、_* は切片が統計的に有意ではないが、線形係数は有意であることを示しています。
- Significance of Coefficients (Polynomial)- 多項式モデルの切片、線形係数、および 2 乗係数が 90% の信頼度で統計的に有意であるかどうかを示す 3 文字のコード。 たとえば、*_* は切片が統計的に有意であり、線形係数が統計的に有意ではなく、2 乗係数が統計的に有意であることを示しています。
注意:
従属変数と説明変数の間に統計的に有意な関係がない各フィーチャでは、回帰係数に関連するすべてのフィールドが NULL または空の文字列になります。
ヒント
[ローカル 2 変数リレーションシップ (Local Bivariate Relationships)] ツールを使用する際は、次のヒントを検討してください。
- 弱い関係に対するツールの感度を制御するには、[縮尺係数] パラメーターを使用します。 縮尺係数をゼロに近い値にすると変数の強い関係のみが検出され、1 に近い値にすると弱い関係も追加で検出できます。 デフォルト値 0.5 は、強~中程度の関係を検出する妥協点です。
- 選択した [近傍数] パラメーター値には、いくつかの重要な意味があります。 近傍数が多ければ、仮説検定に対して使用できるデータも多くなるため、有意な関係を検出できる可能性も高くなります。 ただし、近傍数が多くなると検定の局所性が低下します。さらに遠方まで近傍を検索しなければならなくなり、ごく局所的な関係を検出できる可能性が低くなるからです。 近傍数が多くなると、ツールの実行時間も急増します。
- 選択した [順列の数] パラメーター値は、精度と増加する処理時間のバランス調整に使用します。 順列の数を多くすると、疑似 p 値の範囲が広くなり、結果的に精度が上がります。 たとえば、順列の数が 99 の場合は疑似 p 値の精度が .01 になり、順列の数が 999 の場合は疑似 p 値の精度が .001 になります。 これらの値は、1 を順列の数で除算して、それに 1 を足すことで計算されます: (1/(1+99)、1/(1+999))。 初期段階で問題を調査する場合には順列の数を少なくしてもかまいませんが、通常は順列の数を増やし、最終結果に適した最大数にすることが最善策です。 また、多数の近傍数を使用する場合は、順列の数を増やすこともお勧めします。
引用
- Guo, D. "Local entropy map: a nonparametric approach to detecting spatially varying multivariate relationships." International Journal of Geographical Information Science 24, no. 9 (September 2010): 1367-1389.