[地理空間加重回帰分析 (Geographically Weighted Regression)] ツールでは、地理分野とその他の分野で用いられる空間回帰手法の 1 つである地理空間加重回帰分析 (GWR) を使用します。 GWR は、データセット内のあらゆるフィーチャに回帰方程式をあてはめることで、理解または予測しようとしている変数またはプロセスのローカル モデルを評価します。 GWR では、各ターゲット フィーチャの近傍内に存在するフィーチャの従属変数と説明変数を組み込んで、このような別々の方程式を作成します。 [地理空間加重回帰分析 (Geographically Weighted Regression)] ツールを使用すると、各近傍の形状と範囲が [近傍タイプ] パラメーターと [近傍選択方法] パラメーターの値に基づいて解析されます。 このツールでは、連続 (ガウス)、バイナリ (二項)、およびカウント (ポワソン) データを従属変数として使用できます。 GWR は、数百以上のフィーチャを含むデータセットで使用します。
注意:
[マルチスケール地理空間加重回帰分析 (Multiscale Geographically Weighted Regression)] ツールでは、従属変数と説明変数の間のさまざまなスケールの関係を使用して、データに対して GWR を実行できます。
適用例
[地理空間加重回帰分析 (Geographically Weighted Regression)] ツールは、次のようなさまざまな質問に答えることができます。
- 学歴と所得の間のリレーションシップは、分析範囲全体にわたって一貫性があるか。
- 水塊フィーチャに近ければ近いほど特定の病気の発生率が高いか。
- 森林火災の高い頻度を説明する主要な変数はどれか。
- 絶滅のおそれのある種を再野生化するために保護する必要のある生息地はどれか。
- 生徒が試験で高成績をあげている地域はどこか。 どのような特性が関連付けられているか。 各特性が最も重要なのはどこか。
- 高いガン罹患率に影響を及ぼす要因は、分析範囲全体にわたって一貫性があるか。
入力
[地理空間加重回帰分析 (Geographically Weighted Regression)] ツールを実行するには、[入力フィーチャ] パラメーターに、従属変数を表す 1 つのフィールドと説明変数を表す 1 つ以上のフィールドを指定します。 これらのフィールドは、数値で値の範囲を持つ必要があります。 従属変数または説明変数に欠損値があるフィーチャは、解析から除外されます。ただし、[欠損値の補完 (Fill Missing Values)] ツールを使用して、[地理空間加重回帰分析 (Geographically Weighted Regression)] ツールを実行する前にデータセットを完成させておくことができます。 次に、解析するデータに基づいて、モデル タイプを選択する必要があります。 データに適したモデルを使用することが重要です。 各モデル タイプの説明と、データに適したモデル タイプを特定する方法を次に示します。
モデル タイプ
[地理空間加重回帰分析 (Geographically Weighted Regression)] ツールには、連続、バイナリ、カウントという 3 種類の回帰モデルが用意されています。 これらのタイプの回帰はそれぞれ、最小二乗法、ロジスティック、ポワソンとして知られています。 解析における [モデル タイプ] パラメーターの値は、従属変数が計測または集計された方法と、この変数に含まれる値の範囲に基づいて決定します。
連続 (ガウス)
[連続 (ガウス分布)] オプションは、従属変数が広範な値 (温度や総売上額など) を取ることができる場合に使用します。 従属変数が正規分布しているのが理想的です。 従属変数のヒストグラムを作成すると、その従属変数が正規分布しているかどうかを確認できます。 ヒストグラムが左右対称の釣鐘曲線である場合は、ガウス分布モデル タイプを使用します。 大半の値は平均値付近に集まり、平均値から根本的に外れた値はほとんどありません。 平均値の左側にも右側と同様に多数の値があります (分布の平均値と中央値は同じになります)。 従属変数が正規分布していないように見える場合は、その変数をバイナリ変数に再分類することを検討します。 たとえば、従属変数が平均世帯収入である場合は、その変数を再コーディングして、1 が全国の収入中央値を上回ることを示し、0 が全国の収入中央値を下回ることを示すバイナリ変数にすることができます。 連続フィールドは、[フィールド演算 (Calculate Field)] ツールの [再分類] ヘルパー関数を使用して、バイナリ フィールドに再分類できます。
バイナリ (ロジスティック)
[バイナリ (ロジスティック)] オプションは、従属変数が 2 つの値 (成功と失敗や存在と不在など) のいずれかを取ることができる場合に使用します。 従属変数を含むフィールドは数値で、1 と 0 のみを含む必要があります。 対象のイベント (成功や動物の存在など) をコーディングする場合、回帰は 1 の確立をモデル化するため、結果の解釈が容易になります。 グローバルとローカルの両方で、データ内に 1 と 0 のばらつきが存在するはずです。 [近傍統計サマリー (Neighborhood Summary Statistics)] ツールを使用すると、ローカル近傍の標準偏差を計算して、同じ値を持つすべてのエリアを特定することができます。
カウント (ポワソン)
[カウント (ポワソン分布)] オプションは、従属変数が不連続であり、イベントの発生回数 (犯罪件数など) を表す場合に使用します。 従属変数が比率を表し、その比率の分母が固定値である場合 (1 か月あたりの売上や人口 10,000 人あたりのガン患者の数など) にも、カウント モデルを使用できます。 従属変数の値は、負の値にすることも、小数を含む値にすることもできません。
近傍タイプ
近傍は、各ローカル回帰方程式に使用される距離バンドまたは近傍数であり、局所的にモデルを推定する方法を制御する [地理空間加重回帰分析 (Geographically Weighted Regression)] ツールで考慮すべき最も重要なパラメーターになる可能性があります。 各近傍の形状と範囲は、[近傍タイプ] パラメーターと [近傍選択方法] パラメーターの値に基づいて解析されます。
固定近傍数または距離バンドという 2 つの近傍タイプのいずれかを選択することができます。 近傍数が固定されている場合、各近傍のエリアは、近傍ポイントの密度によって決まります。つまり、フィーチャが密集しているエリアでは近傍が小さくなり、フィーチャがまばらなエリアでは近傍が大きくなります。 距離バンドを使用する場合、近傍サイズは分析範囲内の各フィーチャで一定のままになります。このため、フィーチャが密集している場合は、近傍ごとのフィーチャ数が多くなり、フィーチャがまばらな場合は、近傍ごとのフィーチャ数が少なくなります。
近傍選択方法には、近傍サイズの決定方法 (実際の距離または使用される近傍の数) を指定します。 [黄金探索] または [手動間隔] オプションで選択された近傍は、補正赤池情報量基準 (AICc) の値の最小化に基づきます。 また、[ユーザー定義] オプションで特定の近傍距離または近傍数を設定することもできます。
[黄金探索] 選択方法の場合、このツールは、黄金分割探索方法を使用して、距離バンドまたは近傍数に最適な値を決定します。 この方法では、まず最大距離と最小距離を特定し、これらの間のさまざまな距離で段階的に AICc をテストします。 最大距離は、各フィーチャに近傍としての入力フィーチャ数の半数が含まれる距離になり、最小距離は、各フィーチャに近傍としてのデータセット内のフィーチャ数の少なくとも 5% が含まれる距離になります。
[最小検索距離] および [最大検索距離] パラメーター (距離バンドの場合) と [最小近傍数] および [最大近傍数] パラメーター (近傍数の場合) を使用して、黄金探索の検索範囲を絞ることができます。
注意:
近傍パラメーターで 1,000 を超える近傍が生成された場合は、最も近い 1,000 の近傍だけが使用されます。
ローカル加重方式
GWR の機能は、各ローカル回帰方程式で使用されるフィーチャに地理空間的な加重を適用することです。 フィーチャが回帰ポイントから遠ざかるにつれて、加重が小さくなり、ターゲット フィーチャの回帰結果に与える影響も小さくなります。フィーチャが回帰ポイントに近づくにつれて、回帰方程式で加重が大きくなります。 加重は、カーネルを使用して決定されます。カーネルは、距離が長くなるにつれて加重がどれだけ速く減少するかを求める関数です。 [地理空間加重回帰分析 (Geographically Weighted Regression)] ツールには、[ローカル加重方式] パラメーターのカーネル オプションとして [ガウス] および [バイスクエア] という 2 つのオプションが用意されています。
ガウス加重方式では、フォーカル フィーチャに加重 1 が割り当てられ、フォーカル フィーチャからの距離が長くなるにつれて、近傍フィーチャの加重が徐々に減少していきます。 たとえば、2 つのフィーチャが 0.25 の帯域幅だけ離れている場合、方程式で結果として生成される加重は約 0.88 になります。 これらのフィーチャが 0.75 の帯域幅だけ離れている場合、結果として生成される加重は約 0.32 にしかなりません。 ガウス加重方式は、0 に到達することはありませんが、回帰フィーチャから遠いフィーチャの重みをかなり小さくして、回帰にほとんど影響しないようにすることができます。 ガウス加重方式を使用すると、入力データ内の他のすべてのフィーチャは近傍フィーチャになるため、加重が割り当てられます。 ただし、計算効率を上げるため、近傍フィーチャの数が 1000 を超える場合は、最も近い 1000 個だけが各ローカル回帰に組み込まれます。 ガウス加重方式では、各回帰フィーチャが確実に多くの近傍を持つため、これらの近傍の値にばらつきが生じる可能性が高くなります。 これにより、ローカル多重共線性という、地理空間加重回帰分析でよく見られる問題を回避できます。 近傍フィーチャの影響がなだらかに徐々に重要でなくなっていくが、周囲のフィーチャがどれだけ離れているかに関係なく、その影響が常に存在する場合は、[ガウス] 加重方式を使用します。
バイスクエア加重方式は、ガウスによく似ています。 この方式では、フォーカル フィーチャに加重 1 が割り当てられ、フォーカル フィーチャからの距離が長くなるにつれて、近傍フィーチャの加重が徐々に減少していきます。 ただし、指定された近傍の外側にあるすべてのフィーチャに 0 が割り当てられ、それらのフィーチャはターゲット フィーチャのローカル回帰に影響を及ぼしません。 同じ近傍指定でバイスクエア加重方式とガウス加重方式を比較すると、バイスクエアの方が、加重が速く減少します。 バイスクエア加重方式を使用する場合は、距離を指定して、その距離を超えるフィーチャが回帰結果に影響を与えないようにすることができます。 バイスクエアは特定の距離を超えるフィーチャを除外するため、適切なローカル回帰分析を実行するための十分なフィーチャ (影響を持つ) が周囲の近傍に存在するという保証はありません。 近傍フィーチャの影響が徐々に重要でなくなり、ある距離を超えるとその影響が完全になくなる場合は、ガウス加重方式を使用します。 たとえば、住宅価格のモデル化に回帰がよく使用され、周囲の住宅の販売価格が共通の説明変数となります。 これらの周囲の住宅は、比較可能な物件と呼ばれます。 融資機関は、比較可能な住宅が最大距離内にあることを必要とする規則を設定することがあります。 この例では、融資機関が指定した最大距離に相当する近傍でバイスクエア加重方式を使用できます。
推定
作成された回帰モデルを使用すると、[予測位置] パラメーターで同じ分析範囲内の他のフィーチャ (ポイントまたはポリゴン) を指定して、これらのフィーチャを予測できます。 予測位置には、入力フィーチャ内の説明変数ごとに一致したフィールドが必要となります。 入力フィーチャ内のフィールド名と予測位置が同じでない場合は、[照合する説明変数] パラメーターで対応するフィールドを照合する必要があります。 照合する場合は、各フィールドを同じタイプにする必要があります (たとえば、double タイプのフィールドを integer タイプのフィールドと照合することはできません)。
係数ラスター
大部分の回帰モデルと比較した場合の GWR の主なメリットは、空間的に変化する関係を探索できることです。 説明変数と従属変数の関係の空間的な変化を視覚化する 1 つの方法は、係数ラスターを作成することです。 パス名を [係数ラスター ワークスペース] パラメーターの値として指定すると、[地理空間加重回帰分析 (Geographically Weighted Regression)] ツールはモデルの切片および各説明変数の係数ラスター サーフェスを作成します。 ラスターの解像度は [セル サイズ] 環境で制御されます。 近傍タイプと加重方式に基づいて、各ラスター セルの周囲に近傍が作成されます。 ラスター セルの中心から近傍内のすべての入力フィーチャまでの加重が算出され、これらの加重を使用して、そのラスター セルに一意の回帰方程式が求められます。 近傍と加重はセルごとに変化するため、係数もラスター セルごとに異なります。
注意:
現在、GWR モデルの係数への信頼度を評価する方法についてのコンセンサスはありません。 これまでは t-検定を使用して、係数の推定値が 0 と大きく異なるかどうかに基づいて推測されてきましたが、この手法の妥当性については、まだ盛んに研究が行われています。 非公式に係数を評価する 1 つの手法は、関連する標準誤差で推定のマグニチュードをスケーリングする方法として、各フィーチャに提供された標準誤差で係数を除算し、それらの結果を視覚化して、それらの係数に比べて標準誤差の高いクラスターを探すことです。
出力
[地理空間加重回帰分析 (Geographically Weighted Regression)] ツールでは、さまざまな出力が生成されます。 GWR モデルのサマリーと統計サマリーは、メッセージとして返されます。 このツールでは、出力フィーチャクラスとチャートだけでなく、必要に応じて、予測フィーチャと係数ラスター サーフェスも生成されます。 出力フィーチャと関連チャートが [コンテンツ] ウィンドウに自動的に追加され、残差をモデル化できるようにホットおよびコールド レンダリング方式が適用されます。 生成される診断とチャートは、指定したモデル タイプによって決まります。
連続 (ガウス)
ガウス モデル タイプでは、従属変数の値が連続であると仮定されます。
出力フィーチャ
出力フィーチャには、回帰残差に加えて、従属変数の観測値と予測値、条件数、ローカル R2、説明変数の係数、および標準誤差のフィールドも含まれます。 マップでは、出力フィーチャがレイヤーとして追加され、標準化残差でシンボル表示されます。 正の標準化残差は、従属変数の値が予測値よりも大きいこと (過小予測) を意味し、負の標準化残差は、従属変数の値が予測値よりも小さいこと (過大予測) を意味します。
切片、切片の標準誤差、係数、各説明変数の標準誤差、予測、残差、標準化残差、影響、Cook の D、ローカル R2、および条件数の値も報告されます。 これらのフィールドの多くは、「最小二乗法による回帰分析の詳細」で説明しています。 影響の値と Cook の D の値はいずれも、回帰係数の推定へのフィーチャの影響を測定します。 ヒストグラム チャートを使用して、一部のフィーチャが残りのデータセットよりも影響力が大きいかどうかを特定できます。 これらのフィーチャは多くの場合、係数の推定を歪ませる外れ値となり、これらのフィーチャを削除してツールを再実行することでモデルの結果が改善される場合があります。 ローカル R2 の値の範囲は 0 ~ 1 であり、フィーチャのローカル モデルの相関関係の強さを表しています。 条件数とは、推定係数の安定性の計測値です。 条件数がおよそ 1000 を上回る場合は、モデルに安定性がないことになります。通常は説明変数同士の相関関係が高い場合にこのような現象が発生します。
メッセージと診断の解釈
解析されたフィーチャの数、従属変数と説明変数、指定された近傍の数など、解析の詳細はメッセージで提供されます。 また、さまざまなモデル診断も報告されます。
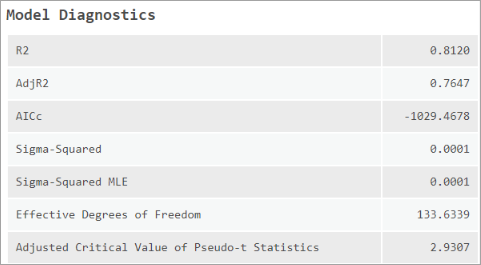
- R2 - 相関係数の二乗は、近似性を計測するための基準です。 値は 0.0 ~ 1.0 で、値が高い方が推奨されます。 これは、回帰モデルによって説明される従属変数の分散の比率として解釈できます。 R2 の計算に使用される分母は、二乗された従属変数の値の合計です。 モデルに説明変数を追加した場合、分母は変化しませんが、分子は変化するため、モデルの適合度が向上した印象を与えます (実際には向上していない可能性もあります)。 下記の AdjR2 をご参照ください。
- AdjR2 - R2 の値には上記の問題があるため、調整済み相関係数の二乗の値を算出することで、分子と分母がその自由度によって正規化されます。 これには、モデル内の変数の数を補正する効果があります。したがって、AdjR2 の値は、ほとんどの場合に R2 の値よりも小さくなります。 ただし、この調整を行うことで、値を因子寄与の割合として解釈することができなくなります。 GWR では、有効自由度は使用される近傍の関数であるため、[一般化線形回帰分析 (Generalized Linear Regression)] ツールで使用されているようなグローバル モデルと比較すると調整が顕著になる場合があります。 このため、モデルを比較する方法としては AICc が最適です。
- AICc - これは、モデルのパフォーマンスを計測するための基準であり、回帰モデルの比較に使用できます。 モデルの複雑さを考慮すると、AICc の値が小さければ小さいほど、観測されたデータにより近似していることを示します。 AICc は、近似性を正確に計測するための基準ではなく、説明変数が (同じ従属変数に適用されるが) 異なる複数のモデルを比較するための基準です。 2 つのモデルの AICc 値の差が 3 より大きい場合は、AICc 値が小さい方のモデルがより適切なモデルと見なされます。 GWR の AICc 値と一般化線形回帰分析 (GLR) の AICc 値を比較すると、グローバル モデル (GLR) からローカル回帰モデル (GWR) に移行することの利点を評価できます。
すべてのモデル タイプの AICc を計算する際に使用する式については、「参考資料」セクションの「Gollini et al.」をご参照ください。
- シグマ 2 - 残差の分散の最小二乗推定 (標準偏差の二乗)です。 この統計情報の値を小さくすることをお勧めします。 この値は、正規化された二乗残差和です (二乗残差和は残差の有効自由度で除算されます)。 シグマ 2 は、AICc の計算に使用されます。
- シグマ 2 MLE - 残差の分散の最尤法推定 (標準偏差の二乗)です。 この統計情報の値を小さくすることをお勧めします。 この値は、二乗残差和を入力フィーチャの数で割って計算されます。
- 有効自由度 - この値は、近似値の分散と係数推定のバイアスの間のトレードオフを反映し、近傍サイズの選択に影響を与えます。 近傍が無限に近づくと、すべてのフィーチャの地理空間加重は 1 に近づき、係数推定はグローバルな GLR モデルの係数推定に非常に近くなります。 近傍が非常に大きい場合、係数の有効数が実数に近づき、ローカル係数推定の分散は小さくなりますが、バイアスは大きくなります。 反対に、近傍が小さくなって 0 に近づくと、すべてのフィーチャの地理空間加重は、回帰ポイントを除いて、0 に近づきます。 近傍が非常に小さい場合、係数の有効数は観測の数になり、ローカルの係数推定の分散は大きくなり、バイアスは小さくなります。 有効数は、他の多くの診断基準を計算するために使用されます。
- 疑似 t 統計の調整済みの臨界値 - 両面 t 検定において、95 % の信頼度で係数の統計的有意性をテストするために使用する調整済みの臨界値です。 値は有意水準 (アルファ) 0.05 に対応しており、有効な自由度で除算されます。 この調整は説明変数の有意性のファミリーワイズ エラー率 (FWER) を制御します。
出力チャート
このツールでは、散布図マトリックスとヒストグラムが [コンテンツ] ウィンドウに出力されます。 散布図マトリックスには、1 つの従属変数と 9 つまでの説明変数が含まれています。 ヒストグラムには、逸脱残差と正規分布曲線が表示されます。
バイナリ (ロジスティック)
バイナリ モデル タイプでは、従属変数の値がバイナリ値 (0 または 1) であると仮定されます。
フィーチャクラスと追加フィールド
切片 (INTERCEPT)、切片の標準誤差 (SE_INTERCEPT)、係数、および各説明変数の標準誤差のフィールドと、1 である確率、予測、逸脱残差、GInfluence、およびローカルの逸脱 % の値が報告されます。
メッセージと診断の解釈
解析されたフィーチャの数、従属変数と説明変数、指定された近傍の数など、解析の詳細はメッセージで提供されます。 また、次の診断も報告されます。
- グローバル モデルで説明される逸脱 % (非空間) - これは適合度を計測するための基準であり、グローバル モデル (GLR) のパフォーマンスを定量化します。 値は 0.0 ~ 1.0 で、値が高い方が推奨されます。 これは、回帰モデルによって説明される従属変数の分散の比率として解釈できます。
- ローカル モデルで説明される逸脱 % - これは近似性を計測するための基準で、ローカルなモデル (GWR) のパフォーマンスを定量化します。 値は 0.0 ~ 1.0 で、値が高い方が推奨されます。 これは、ローカルの回帰モデルによって説明される従属変数の分散の比率として解釈できます。
- ローカル モデル対グローバル モデルで説明される逸脱 % - この比率は、ローカルなモデルの二乗残差和をグローバルなモデルの二乗残差和と比較して、グローバルなモデル (GLR) からローカルの回帰モデル (GWR) に移行することの利点を評価する 1 つの方法です。 値は 0.0 ~ 1.0 で、値が高いほど、ローカルの回帰モデルがグローバルなモデルよりも適切に実行されたことを示します。
- AICc - これは、モデルのパフォーマンスを計測するための基準であり、回帰モデルの比較に使用できます。 モデルの複雑さを考慮すると、AICc の値が小さければ小さいほど、観測されたデータにより近似していることを示します。 AICc は、近似性を正確に計測するための基準ではなく、説明変数が (同じ従属変数に適用されるが) 異なる複数のモデルを比較するための基準です。 2 つのモデルの AICc 値の差が 3 より大きい場合は、AICc 値が小さい方のモデルがより適切なモデルと見なされます。 GWR の AICc 値と最小二乗法 (OLS) の AICc 値を比較すると、グローバル モデル (OLS) からローカル回帰モデル (GWR) に移行することの利点を評価できます。
- シグマ 2 - この値は、正規化された二乗残差和です (二乗残差和は残差の有効自由度で除算されます)。 これは、残差の分散の最小二乗推定 (標準偏差の二乗)です。 この統計情報の値を小さくすることをお勧めします。 シグマ 2 は、AICc の計算に使用されます。
- シグマ 2 MLE - この値は、残差の分散の MLE (標準偏差の二乗)です。 この統計情報の値を小さくすることをお勧めします。 この値は、二乗残差和を入力フィーチャの数で割って計算されます。
- 有効自由度 - この値は、近似値の分散と係数推定のバイアスの間のトレードオフを反映し、近傍サイズの選択に影響を与えます。 近傍が無限に近づくと、すべてのフィーチャの地理空間加重は 1 に近づき、係数推定はグローバルな GLR モデルの係数推定に非常に近くなります。 近傍が非常に大きい場合、係数の有効数が実数に近づき、ローカル係数推定の分散は小さくなりますが、バイアスは大きくなります。 反対に、近傍が小さくなって 0 に近づくと、すべてのフィーチャの地理空間加重は、回帰ポイントを除いて、0 に近づきます。 近傍が非常に小さい場合、係数の有効数は観測の数になり、ローカルの係数推定の分散は大きくなり、バイアスは小さくなります。 有効数は、他の多くの診断基準を計算するために使用されます。
- 疑似 t 統計の調整済みの臨界値 - 両面 t 検定において、95 % の信頼度で係数の統計的有意性をテストするために使用する調整済みの臨界値です。 値は有意水準 (アルファ) 0.05 に対応しており、有効な自由度で除算されます。 この調整は説明変数の有意性の FWER を制御します。
出力チャート
散布図マトリックス、箱ひげ図、および逸脱残差のヒストグラムが提供されます。
カウント (ポワソン)
ポワソン モデル タイプでは、従属変数の値がカウントであると仮定されます。
フィーチャクラスと追加フィールド
出力フィーチャには、切片 (INTERCEPT)、切片の標準誤差 (SE_INTERCEPT)、係数、および各説明変数の標準誤差のフィールドと、対数変換前の予測 (RAW_PRED)、予測、逸脱残差、GInfluence、ローカルの逸脱 %、および条件数の値が含まれます。
メッセージと診断の解釈
解析されたフィーチャの数、従属変数と説明変数、指定された近傍の数など、解析の詳細はメッセージで提供されます。 また、次の診断も報告されます。
- グローバル モデルで説明される逸脱 % (非空間) - これは適合度を計測するための基準であり、グローバル モデル (GLR) のパフォーマンスを定量化します。 値は 0.0 ~ 1.0 で、値が高い方が推奨されます。 これは、回帰モデルによって説明される従属変数の分散の比率として解釈できます。
- ローカル モデルで説明される逸脱 % - これは近似性を計測するための基準で、ローカルなモデル (GWR) のパフォーマンスを定量化します。 値は 0.0 ~ 1.0 で、値が高い方が推奨されます。 これは、ローカルの回帰モデルによって説明される従属変数の分散の比率として解釈できます。
- ローカル モデル対グローバル モデルで説明される逸脱 % - この比率は、ローカルなモデルの二乗残差和をグローバルなモデルの二乗残差和と比較して、グローバルなモデル (GLR) からローカルの回帰モデル (GWR) に移行することの利点を評価する 1 つの方法です。 値は 0.0 ~ 1.0 で、値が高いほど、ローカルの回帰モデルがグローバルなモデルよりも適切に実行されたことを示します。
- AICc - これは、モデルのパフォーマンスを計測するための基準であり、回帰モデルの比較に使用できます。 モデルの複雑さを考慮すると、AICc の値が小さければ小さいほど、観測されたデータにより近似していることを示します。 AICc は、近似性を正確に計測するための基準ではなく、説明変数が (同じ従属変数に適用されるが) 異なる複数のモデルを比較するための基準です。 2 つのモデルの AICc 値の差が 3 より大きい場合は、AICc 値が小さい方のモデルがより適切なモデルと見なされます。 GWR の AICc 値と OLS の AICc 値を比較することで、グローバルなモデル (OLS) からローカルの回帰モデル (GWR) に移行することの利点を評価できます。
- シグマ 2 - この値は、正規化された二乗残差和です (二乗残差和は残差の有効自由度で除算されます)。 これは、残差の分散の最小二乗推定 (標準偏差の二乗)です。 この統計情報の値を小さくすることをお勧めします。 シグマ 2 は、AICc の計算に使用されます。
- シグマ 2 MLE - この値は、残差の分散の MLE (標準偏差の二乗)です。 この統計情報の値を小さくすることをお勧めします。 この値は、二乗残差和を入力フィーチャの数で割って計算されます。
- 有効自由度 - この値は、近似値の分散と係数推定のバイアスの間のトレードオフを反映し、近傍サイズの選択に影響を与えます。 近傍が無限に近づくと、すべてのフィーチャの地理空間加重は 1 に近づき、係数推定はグローバルな GLR モデルの係数推定に非常に近くなります。 近傍が非常に大きい場合、係数の有効数が実数に近づき、ローカル係数推定の分散は小さくなりますが、バイアスは大きくなります。 反対に、近傍が小さくなって 0 に近づくと、すべてのフィーチャの地理空間加重は、回帰ポイントを除いて、0 に近づきます。 近傍が非常に小さい場合、係数の有効数は観測の数になり、ローカルの係数推定の分散は大きくなり、バイアスは小さくなります。 有効数は、他の多くの診断基準を計算するために使用されます。
- 疑似 t 統計の調整済みの臨界値 - 両面 t 検定において、95 % の信頼度で係数の統計的有意性をテストするために使用する調整済みの臨界値です。 値は有意水準 (アルファ) 0.05 に対応しており、有効な自由度で除算されます。 この調整は説明変数の有意性の FWER を制御します。
出力チャート
[コンテンツ] ウィンドウに、散布図マトリックス (最大 19 の変数を含む) と、逸脱残差と正規分布ラインのヒストグラムが表示されます。
他の実装メモとヒント
GLR のようなグローバル回帰モデルでは、複数の変数が多重共線性を示すと (複数の変数が冗長であるか、同じストーリーを語るとき)、結果は信頼できません。 [地理空間加重回帰分析 (Geographically Weighted Regression)] ツールは、データセット内のフィーチャごとにローカル回帰方程式を作成します。 特定の説明変数の値が空間的にクラスターを形成すると、ローカル多重共線性の問題が生じる可能性が高くなります。 出力フィーチャクラスの条件数は、ローカル多重共線性によって結果が不安定になるタイミングを示します。 条件数が 30 を上回っているか、NULL であるか、シェープファイルの場合に -1.7976931348623158e+308 であるフィーチャの結果には信頼性がありません。 条件数は、モデル内の説明変数の数を補正するようにスケール調整されます。 これによって、異なる数の説明変数を使用するモデル間で条件数を直接比較できるようにします。
モデル設計のエラーは、多くの場合、グローバルまたはローカルに多重共線性の問題があることを示しています。 どこに問題があるかを特定するには、[地理空間加重回帰分析 (Geographically Weighted Regression)] ツールを実行して、各説明変数の VIF 値を確認します。 大きい VIF 値がある場合は (たとえば 7.5 を上回る)、グローバル多重共線性によって、このツールで解が求められなくなります。 しかし、もっと可能性が高いのは、ローカル多重共線性の問題です。 各独立変数の主題図を作成してみてください。 主題図で同一値が空間的にクラスターを形成している場合は、モデルからそのような変数を除外するか、別の独立変数と組み合わせて値のばらつきを増やします。 たとえば、住宅の価値をモデル化していて、寝室と風呂に変数がある場合は、両方を組み合わせて値のばらつきを増やすか、それぞれを風呂と寝室の面積として表します。 GWR モデルを構築する際には、ガウス分布またはポワソン分布モデル タイプに空間様式の人為変数またはバイナリ変数を使用したり、ロジスティック モデル タイプで空間クラスターとなっているカテゴリ変数または名目変数を使用したり、可能性のある値が非常に限られている変数を使用したりしないでください。
ローカル多重共線性の問題のために、このツールで最適な距離バンドまたは近傍数の解が求められないこともあります。 手動間隔、ユーザー定義の距離バンド、または具体的な近傍数を指定してください。 この後、出力フィーチャ内の条件数を調査し、ローカル多重共線性の問題に関係しているフィーチャ (条件数が 30 を超えている) を確認します。 このようなフィーチャを一時的に除外して、最適な距離または近傍数を特定したいと思うことがあります。 しかし、条件数が 30 を超えるような結果は信頼できないことを忘れないでください。
参考資料
GLR と GWR の詳細を確認できるリソースがいくつかあります。 まず「回帰分析の基礎」を参照するか、「回帰分析チュートリアル」を学習してください。
次のリソースも有用です。
Brunsdon, C., Fotheringham, A. S., & Charlton, M. E. (1996). "Geographically weighted regression: a method for exploring spatial nonstationarity". Geographical analysis, 28(4), 281-298.
Fotheringham, Stewart A., Chris Brunsdon, and Martin Charlton. Geographically Weighted Regression: The analysis of spatially varying relationships. John Wiley & Sons, 2002.
Gollini, I., Lu, B., Charlton, M., Brunsdon, C., & Harris, P. (2015). "GWmodel: An R Package For Exploring Spatial Heterogeneity Using Geographically Weighted Models." Journal of Statistical Software, 63(17), 1–50.https://doi.org/10.18637/jss.v063.i17.
Mitchell, Andy. The ESRI Guide to GIS Analysis, Volume 2. ESRI Press, 2005.
Nakaya, T., Fotheringham, A. S., Brunsdon, C., & Charlton, M. (2005). "Geographically weighted Poisson regression for disease association mapping". Statistics in medicine, 24(17), 2695-2717.
Páez, A., Farber, S., & Wheeler, D. (2011). "A simulation-based study of geographically weighted regression as a method for investigating spatially varying relationships". Environment and Planning A, 43(12), 2992-3010.