[トレンド (Trend)] ツールは、グローバルな多項式内挿を使用して、数学関数 (多項式) で指定されたスムーズなサーフェスにより入力のサンプル ポイントを近似します。 トレンド サーフェスは徐々に変化し、大まかにデータのパターンを捕捉します。
概念的背景
概念的には、トレンド内挿法は、(値の高さに) 突出した複数のポイント間に 1 枚の紙をかぶせる処理と考えることができます。 以下の図に、緩やかな傾斜を持つ丘で収集した標高のサンプル ポイントのセットについてこれを示します。 紙はマゼンタで表しています。
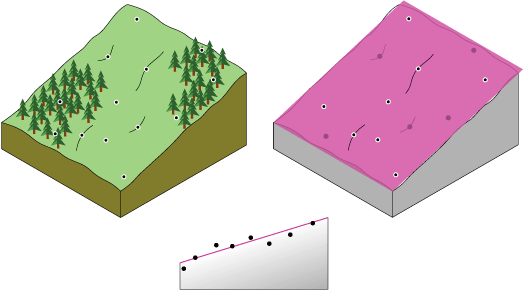
平坦な 1 枚の紙では、谷のある地形を正確に表すことができません。 ただし、紙を 1 回折り曲げると、より地形に沿わせることができます。 数学式に項を追加すると、平面における曲げのような類似の結果が得られます。 平らな平面 (紙を折り曲げていない状態) は一次多項式 (線形) です。 1 回折り曲げると二次多項式、2 回折り曲げると三次多項式 (以下、同様) になります。 このツールでは、12 回まで曲げることができます。 以下の図に、二次多項式による谷の近似を概念的に示します。
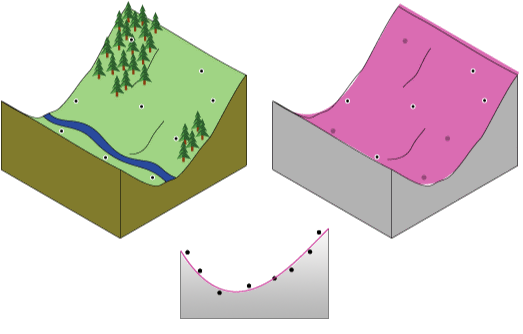
紙が実際の計測ポイントを通ることはめったになく、トレンド内挿法は不正確な内挿法です。 紙の上にあるポイントもあれば、紙の下にあるポイントもあります。 ただし、紙の上にある各ポイントの紙からの距離の合計と、紙の下にある各ポイントの紙からの距離の合計は、近い値になります。 マゼンタで示すサーフェスは、最小二乗回帰を使用して得られたものです。 得られたサーフェスでは、標高の値と紙との差の二乗が最小です。
二乗平均平方根 (RMS) 誤差が小さくなるほど、内挿したサーフェスが入力ポイントをより近く表します。 一般的な多項式の次数は 1 ~ 3 です。 トレンドのサーフェス内挿法はスムーズなサーフェスを作成します。
トレンド内挿法を使用する場合
トレンド内挿法の結果はスムーズなサーフェスで、対象地域に広がるサーフェスで緩やかな傾向を示します。 この種類の内挿法は次の場合に使用できます。
- 対象地域に広がる地域間でサーフェスが徐々に変化する場合に、サーフェスでサンプル ポイントを近似する。たとえば、工業地域に広がる公害。
- 長期間、または地球的なトレンドの効果の検証または除去。 このような場合、この手法はしばしばトレンド サーフェス解析と呼ばれます。
トレンド内挿法は、物理プロセス (公害と風の方向など) を表す低次の多項式を使用して、徐々に変化するサーフェスを作成します。 ただし、多項式が複雑になるほど、物理的な意味をその多項式に帰することが困難になります。 さらに、計算するサーフェスは、特にエッジで外れ値 (極端に高い値や低い値) の影響を大きく受けます。
トレンド内挿法の種類
トレンド内挿法には、「リニア」と「ロジスティック」という 2 つの基本タイプがあります。
線形傾向
[リニア] トレンド サーフェス内挿は浮動小数点のラスターを作成します。 多項式回帰を使用して、最小二乗サーフェスを入力ポイントに適合させます。 この方法を選択した場合、サーフェスの適合で使用する多項式の次数を指定できます。 この方法を理解するため、一次多項式のケースを考えてみましょう。 一次リニア トレンド サーフェス内挿では、入力ポイント セットに最小二乗適合する面が求められます。
トレンドのサーフェス内挿法はスムーズなサーフェスを作成します。 生成されたサーフェスは元のデータ ポイントをほとんど通過しません。これは、サーフェス全体のベスト フィットが求められるためです。 二次以上の多項式を使用して内挿する場合、入力フィーチャ データの入力ファイルの最小と最大を上回るラスターが生成される可能性があります。
ロジスティック トレンド
トレンド サーフェス生成の [ロジスティック] オプションは、空間内の指定した位置 (X,Y) セットについて、特定の現象の有無を確率として予測する場合に適しています。 Z 値はカテゴリ化された確率変数であり、結果は 2 つだけです (たとえば、絶滅危惧種が生存している、またはその種が生存していないなど)。 これら 2 つの Z 値を、それぞれ 1 と 0 としてコード化できます。 このオプションは、セル値に基づいて、1 ~ 0 までの連続した確率グリッドを作成します。
最初にモデルをリニア形式へ変換せずに、最尤法を使用して非線形確率サーフェス モデルを計算します。
出力 RMS ファイル
入力データセット内の位置の値と、内挿ラスター サーフェスの同じ位置の値とを比較し、それによって得られた内挿の二乗平均平方根誤差が RMS エラー ファイルに保存されます。
この RMS 誤差が最小になるように次数値を変更することで、内挿の {order} パラメーターで使用する最適値が決定されます。 カイ二乗値も報告されます。
例
以下に、[多項式の次数] を 3 に設定して実行した [トレンド (Trend)] ツールによる出力 RMS ファイルの例を示します。
coef # coef
------ ----------------
0 -1192066.7888371
1 -1.78479492586755
2 -0.195982103615487
3 -8.87072249743903e-1
4 -2.0538267625596e-1
5 -3.85610088343239e-1
6 -1.46420255709888e-2
7 -5.31539027745154e-2
8 -2.59261094879031e-3
9 9.71651459136166e-4
------ ----------------
RMS Error = 296.957857221845
Chi-Square = 17019506.0103975この 3 次トレンドにおける出力ラスター内の任意の位置の予測値は、一連の方程式から導き出される値を集計することで決定できます。 次の方程式において、x = 位置の経度、y = 緯度、cn 項は前述のテーブルからの係数値です。 この 3 次内挿の方程式は次のとおりです。
Prediction(x,y) = c0 +
x·c1 + y·c2 +
x2·c3 + x·y·c4 + y2·c5 +
x3·c6 + x2·y·c7 + x·y2·c8 + y3·c9
基本的に、係数 0 は常に切片を表します。 ここからは、1 次項で最高次の x から始めて x がなくなるまで反復します。 次に、2 次項で x の次数が下がるまで再び反復します。3 次項についても同様です。
注意:
これらの方程式は次数が増えても同じパターンに従います。 たとえば、4 次が指定された場合、RMS テーブル内に 5 つの値が追加で指定され (係数 10、11、12、13、および 14)、これらの値を使用した同数の方程式が増えます。