クリギングは、Z 値を持つ散らばったポイント セットから推定サーフェスを作成する高度な地球統計学的手法です。 内挿ツールセットの他の内挿法と異なり、[クリギング (Kriging)] ツールでは、Z 値によって表される現象の空間的振舞いを対話的に検証してから、出力サーフェスを生成するための最適な推定方法を選択する必要があります。
クリギングとは
[IDW] (逆距離加重) 内挿ツールおよび [スプライン (Spline)] 内挿ツールは、周囲の計測値または指定した数学式が出力サーフェスの滑らかさを決定し、結果に直接影響することから、決定論的内挿法と呼ばれます。 一方、2 つ目の内挿法のファミリーは、クリギングのような自己相関を含む、つまり相互に統計的な関係を持つ計測値を持つ統計モデルに基づく、地球統計学的な方法で構成されます。 このため、地球統計学的手法は、予測サーフェスを作成できるだけでなく、予測の確実性または精度の尺度も提供します。
クリギングでは、複数のサンプル ポイント間の距離または方向が、サーフェス上の変動の説明に使用できる空間的相関を反映していると仮定しています。 [クリギング (Kriging)] ツールは、指定数のポイント、または指定半径内のすべてのポイントに数学関数を当てはめ、各位置の出力値を決定します。 クリギングは複数ステップのプロセスです。データの予備的統計解析、バリオグラムのモデル化、サーフェスの作成、およびオプションとして分散サーフェスの調査を含みます。 データ内に空間的な相関を持つ距離または方向のバイアスがある場合、クリギングが最適です。 多くの場合、土壌学や地質学で使用されます。
クリギングの式
クリギングは、周囲の計測値を加重して未計測の位置を予測する点で、IDW に似ています。 両方の内挿法の一般的な式は、データの加重合計として構成されます。
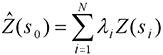
- ここで、
Z(si) = i 番めの位置における計測値
λi = i 番めの位置における計測値の不明な加重
s0 = 予測位置
N = 計測値の数
IDW では、加重 λi、は予測位置までの距離のみで決まります。 ただし、クリギングの手法では、加重は計測ポイントと予測位置との距離だけでなく、計測ポイントの全体的な空間的配置によっても決まります。 加重の空間的配置を使用するには、空間的自己相関を定量化する必要があります。 したがって、通常クリギングでは、加重 λi は計測ポイントの近似モデル、予測位置までの距離、および予測位置周囲の計測値間の空間的関係によって決まります。 次のセクションでは、一般的なクリギングの式を使用して、予測サーフェスを持つマップ、および予測の精度を持つマップを作成する方法について説明します。
クリギングによる予測サーフェス マップの作成
クリギング内挿法で予測を行うには、次の 2 つのタスクが必要です。
- 従属性のルールを発見する。
- 予測を行う。
これらの 2 つのタスクを実現するために、クリギングは次の 2 つのステップを持つプロセスを実行します。
- 自己相関モデル (近似モデル) に依存する統計的従属性 (空間的自己相関と呼ばれる) の値を推定するための、バリオグラムと共分散関数を作成する。
- 未知の値を予測する (予測を行う)。
このように個別タスクが 2 つあるため、クリギングはデータを 2 回使用すると言われています。1 回めはデータの空間的自己相関を推定するため、2 回めは予測を行うためです。
バリオグラフィ
モデル近似、または空間的モデル化は、構造解析やバリオグラフィとも呼ばれます。 計測ポイントの構造の空間モデリングでは、経験的セミバリオグラムのグラフを使用します。距離 h 間隔で配置されたすべての位置ペアについて、次の数式を用いて計算します。
Semivariogram(distanceh) = 0.5 * average((valuei – valuej)2)式では、位置のペアの値の差の二乗が計算されます。
以下の図に、あるポイント (赤のポイント) とその他すべての計測位置とのペアを示します。 各計測ポイントについて、このプロセスが継続されます。
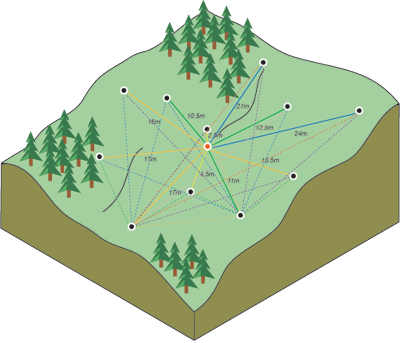
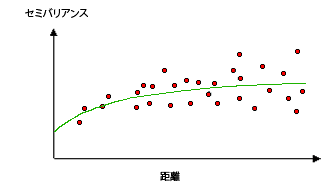
多くの場合、位置の各ペアの距離は一意で、多数のポイントのペアがあります。 すべてのペアをプロットすると、あっという間に手に負えない状態になります。 各ペアをプロットする代わりに、ペアをラグのビンにグループ化します。 たとえば、ポイント間の距離が 40 m より大きく 50 m 未満のポイント ペアのすべてについて、平均セミバリアンスを計算します。 経験的セミバリオグラムは、Y 軸に平均セミバリオグラムの値、X 軸に距離 (またはラグ) を持つグラフです (下図参照)。
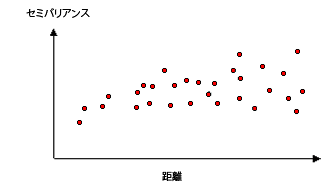
空間的自己相関は、近くにあるものは遠くにあるものよりも似ているという地理の原則を定量化します。 このため、位置のペアが近接しているほど (セミバリオグラム雲の x 軸の左端)、値の類似性は高くなります (セミバリオグラム雲の y 軸の一番下)。 位置のペアの距離が大きい (セミバリオグラムの分布の X 軸の右方に移動) ほど、ペアの類似性は小さくなり、差の二乗の値が大きくなります (セミバリオグラムの分布の Y 軸の上方に移動)。
経験的セミバリオグラムのモデル近似
次のステップでは、経験的セミバリオグラムを形成する各ポイントにモデルを適合させます。 セミバリオグラム モデリングは、空間記述と空間推定の間にある重要なステップです。 クリギングの主な応用として、サンプルが未収集の位置における属性値を推定することがあります。 経験的セミバリオグラムではデータセットの空間的自己相関についての情報が提供されます。 ただし、可能なすべての方向と距離について情報が提供されるわけではありません。 このような訳で、クリギングの推定値が正のクリギング分散となるためには、モデル (つまり、連続する関数または曲線) を経験的セミバリオグラムに適合させる必要があります。 抽象的には、これは、データ ポイントを連続する直線または曲線で近似する回帰分析に似ています。
モデルを経験的セミバリオグラムに適合させるには、モデルとして使用する関数を選択します。たとえば、増加して、一定範囲を超えて距離が大きくなると平坦になる球体タイプの関数を選択します (後述の球モデル例を参照)。 経験的セミバリオグラムのポイントと、モデルには差があります。モデルの曲線の上にあるポイントも、下にあるポイントもあります。 ただし、曲線の上にある各ポイントの距離の合計と、曲線の下にある各ポイントの合計は、近い値になります。 選択できるセミバリオグラムのモデルは多数あります。
セミバリオグラムのモデル
[クリギング (Kriging)] ツールには、経験的セミバリオグラムのモデル化に選択できる次の関数が用意されています。
- 円
- 球
- 指数
- ガウス
- リニア
特に曲線の形状が原点近くで大きく異なる場合、選択したモデルが未知値の推定に影響を与えます。 原点近くの曲線の傾きが大きいほど、最も近い近傍ポイントが推定に与える影響が大きくなります。 この結果として、出力サーフェスは滑らかでなくなります。 各モデルは、さまざまな種類の現象をより正確になぞるように設計されています。
以下の図に、2 つの一般的なモデルと関数の違いを示します。
球モデルの例
このモデルでは、ある距離まで空間的自己相関が徐々に減少 (セミバリアンスが増加) し、その距離を超えると自己相関が 0 になります。 球モデルは、最も一般的に使用されるモデルの 1 つです。
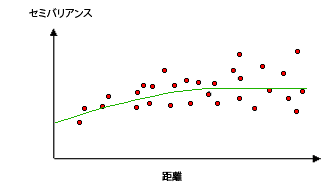
指数モデルの例
このモデルは、距離の増加と共に空間的自己相関が指数的に減少する場合に適用します。 自己相関がまったくなくなるのは、無限大の距離のみです。 指数モデルも、一般的に使用されるモデルです。 使用するモデルの選択は、データの空間的自己相関、および現象に対する事前知識に基づきます。
これらの数学モデルについて詳しくは、この後の説明をご参照ください。
セミバリオグラム - レンジ、シル、およびナゲット
前述したように、セミバリオグラムは測定サンプル ポイントの空間的自己相関を表します。 地理の原則 (近いものほど似る) により、近くにある計測ポイントは通常、遠くにある計測ポイントよりも差の二乗の値が小さくなります。 ビン化後に位置の各ペアをプロットすると、これらにモデルが適合されます。 これらのモデルを説明するために、レンジ、シル、ナゲットが一般的に使用されます。
レンジとシル
セミバリオグラムのモデルを見ると、一定の距離に達すると平坦になっていることがわかります。 モデルが最初に平坦になる距離をレンジと呼びます。 レンジよりも近い距離にあるサンプル位置は、空間的自己相関があります。一方、レンジよりも遠い距離には空間的自己相関はありません。
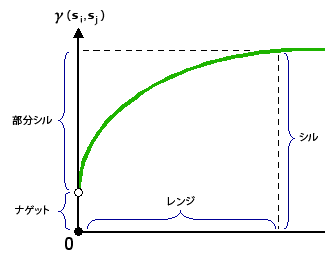
セミバリオグラム モデルがレンジに到達する値 (y 軸の値) のことをシルと呼びます。 パーシャル シルはシルからナゲットを引いた値のことです。 ナゲットについては次のセクションで説明します。
ナゲット
理論上は、分離距離がゼロ (ラグ = 0 など) のときにセミバリオグラムの値は 0 になります。 ただし、限りなく小さい分離距離では、セミバリオグラムは多くの場合ナゲット効果 (0 より大きい値) を示します。 セミバリオグラム モデルの Y 切片が 2 の場合、ナゲットは 2 です。
ナゲット効果は、サンプリング間隔より小さい距離における空間的変動源または測定誤差 (またはその両方) に帰することができます。 測定誤差は測定装置に固有の誤差によって生じます。 自然現象はさまざまなスケールで空間的変動を示します。 サンプリング距離より小さい微小スケールでの変動はナゲット効果の一部として現れます。 データを収集する前に、着目する空間的変動のスケールを理解することが重要です。
予測の実行
データの従属性または自己相関を発見し (「バリオグラフィ」を参照)、データの空間情報を使用して距離を計算し、空間的自己相関をモデル化したら (データの 1 回めの使用)、近似モデルを使用して予測ができます。 その後、経験的セミバリオグラムは使用しません。
これで、データを使用して予測ができます。 IDW 内挿法と同様に、クリギングは、周囲の計測値から加重を作成し未計測の位置を予測します。 IDW 内挿法と同様に、未計測の位置に最も近い計測値が最大の影響をおよぼします。 ただし、クリギングでは、周囲の計測ポイントの加重は、IDW の加重よりも洗練されています。 IDW では距離に基づく単純なアルゴリズムを使用しますが、クリギングの加重は、データの空間的性質に着目して作成されたセミバリオグラムから得られます。 現象の連続サーフェスを作成するために、セミバリオグラム、および近傍の計測値の空間的配置に基づいて解析エリアの各位置、またはセル中心について予測が行われます。
クリギング手法
クリギング手法には、通常型と普遍型の 2 種類があります。
通常クリギングは、最も一般的に幅広く使用されているクリギング手法で、デフォルトです。 通常クリギングでは、定数の平均値が不明だと仮定します。 これを却下する科学的な根拠がない限り、これは妥当な前提です。
ユニバーサル クリギングでは、データに優勢な傾向 (卓越風など) があり、かつこれを決定論的関数の多項式でモデル化できると仮定します。 この多項式が元の計測ポイントから減算され、ランダム誤差から自己相関がモデル化されます。 ランダムなエラーをモデルで近似すると、予測を行う前に多項式が加算され、意味のある結果が得られます。 普遍型クリギングは、データに傾向があることが分かっていて、かつ表す式に科学的な根拠がある場合にのみ使用します。
セミバリオグラム グラフ
クリギングは、このトピックで説明する以上の空間的統計知識を必要とする複雑な手順です。 クリギングを使用する前に、その原理を十分に理解し、入手したデータがこの手法でのモデリングに適しているかどうかを評価する必要があります。 クリギング手法をよく理解していない場合は、このトピックの最後に記載されている文献を参照することをお勧めします。
クリギングは、「Z 値で表される現象の空間的変動がサーフェス全体で統計的に均一である」ことを前提とする地域化変数理論に基づいています (たとえば、サーフェスのすべての場所で同じ変動パターンが認められる場合など)。 この「空間的均一性」の前提が地域化変数理論の基本となります。
数学モデル
以下は、セミバリアンスの説明で使用される数学モデルの一般的な形状と数式です。
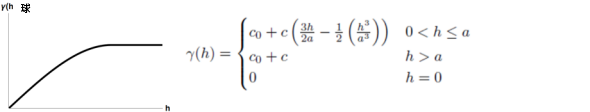
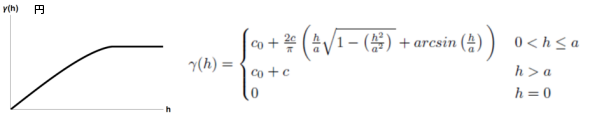
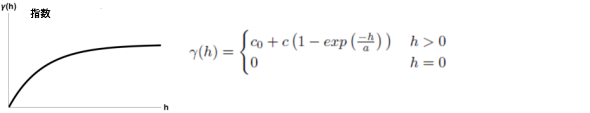
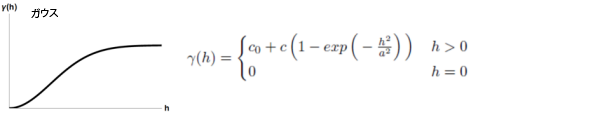
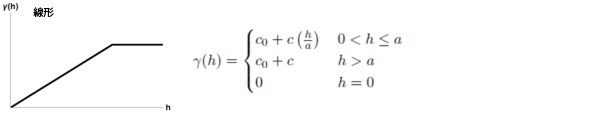
参考文献
Burrough, P. A. Principles of Geographical Information Systems for Land Resources Assessment. New York: Oxford University Press. 1986.
Heine, G. W. "A Controlled Study of Some Two-Dimensional Interpolation Methods." COGS Computer Contributions 3 (no. 2): 60–72. 1986.
McBratney, A. B., and R. Webster. "Choosing Functions for Semi-variograms of Soil Properties and Fitting Them to Sampling Estimates." Journal of Soil Science 37: 617–639. 1986.
Oliver, M. A. "Kriging: A Method of Interpolation for Geographical Information Systems." International Journal of Geographic Information Systems 4: 313–332. 1990.
Press, W. H., S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery. Numerical Recipes in C: The Art of Scientific Computing. New York: Cambridge University Press. 1988.
Royle, A. G., F. L. Clausen, and P. Frederiksen. "Practical Universal Kriging and Automatic Contouring." Geoprocessing 1: 377–394. 1981.