ファジー論理はオーバーレイ解析手法として、候補地選定モデルや適合性モデルなどの従来のオーバーレイ解析の応用について解決する際に使用できます。
ファジー論理の基本的な前提は、属性および空間データのジオメトリに不正確さが存在するということです。 ファジー論理には、この 2 つのタイプの不正確さに対応する手法が用意されていますが、オーバーレイ解析に関連するファジー論理は、属性データの不正確さに重点を置いています。 属性データで不正確さが生じる 2 つの主要な分野は、クラスの定義と現象の計測です。 このような不正確さが原因で、特にクラスの定義において、セルを特定のクラスに割り当てる際に不正確になることがあります。
分類におけるクラスの定義と、現象をクラスに割り当てる際の不正確さは、意思決定に影響を与える可能性があります。 ファジー オーバーレイ ツールによって、意思決定者はこのような不正確さに関する意思決定を下すことができます。 ファジー論理は、クラスの境界の不正確さをモデル化することに重点を置いています。
[加重オーバーレイ (Weighted Overlay)] ツールと [加重合計 (Weighted Sum)] ツールは、各セルがクラスに含まれるか含まれないかのどちらかであるクリスプ集合に基づいています。 特に、ファジー論理はクラス間の境界が明瞭でない状況に対応します。 クリスプ集合とは異なり、ファジー論理はクラスに含まれるか含まれないかを扱うのではなく、現象が集合 (またはクラス) に属する可能性がどれくらいかを定義します。 ファジー論理は集合論に基づいているため、確率ではなく可能性を定義します。
たとえば、住宅適合性モデルにおいて、傾斜角が入力条件の 1 つである場合、各傾斜角の値は、その傾斜角値が建物の適合性集合 (またはクラス) に属する (適合性が高い) 可能性に基づいて 0 〜 1 の値に変換、または値が割り当てられます。 1 はその値が確実に集合に含まれることを示し、0 はその値が確実に集合に含まれないことを示します。 他のすべての値は一定の可能性があることを示し、値が高いほど集合に属する可能性が高いことを示します。 元の入力値を、集合に属する可能性を示す 0 〜 1 の評価尺度に変換する処理を、ファジー化処理と呼びます。 モデルの各条件 (たとえば、傾斜方向、道路までの距離、土地利用タイプ) はファジー化されます。 [ファジー メンバーシップ (Fuzzy Membership)] ツールを使用して、データを 0 〜 1 の可能性尺度に変換します。
すべての条件に最も適合する場所、つまりすべての集合に属する可能性が高い場所を決定するには、[ファジー オーバーレイ (Fuzzy Overlay)] ツールを使用します。 複数の条件を組み合わせる場合、[ファジー オーバーレイ (Fuzzy Overlay)] ツールを使用して、セルが複数の条件によって定義された各集合に属する可能性を調査します。 たとえば、特定の場所が、傾斜角、傾斜方向、および道路までの距離に対して望ましい適合性を示す可能性はどれくらいでしょうか?
このため、オーバーレイ解析のためのファジー論理では、ファジー化 (ファジー メンバーシップ処理) とファジー オーバーレイ解析の 2 つが主なステップになります。 この 2 つのステップは、一般的なオーバーレイ処理における再分類/変換ステップおよび追加/結合ステップにそれぞれ関連しています。
多くの場合、ある現象がクラスに属するかどうかは明瞭ではなく、主観的です。 人間の言葉では、このような不正確さを「非常に」「わずかに」「適度に」などの修飾語で修飾します。 ファジー論理では、より人間の自然な思考に近いオーバーレイ解析が実行されます。 事象は明瞭ではなく、境界はあいまいな場合があります。 ファジー論理では、データの不確実性を解析するのではなく、クラスの境界の不正確さを調査します。
次のセクションでは、データ分類に関する問題、ファジー メンバーシップ処理、ファジー オーバーレイ解析の実行について説明します。 また、ファジー論理とバイナリおよび加重オーバーレイ解析手法との比較、ファジー論理の一般的なオーバーレイ処理への統合方法についても、以下で説明します。
データ分類とファジー論理
現象を説明したり順序付けたりするには、一般的に現象をクラスに特徴付けます。 クラスの例には、土地利用カテゴリ、土壌タイプ、適合性の重み付け、道路クラス、植生タイプなどがあります。 クリスプ集合では、所属 (メンバーシップ) はバイナリ (二値) であり、現象はクラスに含まれるか含まれないかのどちらかです。 クラスの境界ははっきりしています。 ただし、思考の不正確さ、あいまいな分類ルール、漠然性、両価性により、クラス間の境界は必ずしも明瞭ではありません。
たとえば、あるグループ内の人々の身長差を調査する場合に、さまざまな人々を身長に基づいてクラスに分類することから始めるとします。 まず、低、中、高の 3 つのクラスに分類するとします。 この際、クラスの境界を設定する必要があります。 たとえば、身長が低の人々は 5 フィート (1.524 メートル) 以下、高の人々は 6 フィート (1.8288 メートル) 以上、中の人々は 5 ~ 6 フィート (1.6764 ~ 1.8288 メートル) にするとします。 身長が 6 フィート (1.8288 メートル) の人は、高のクラスに配置されます。 身長が 5 フィート 11 インチ (1.8034 メートル) の人は、中に分類されます。 2 人の身長差は 1 インチ (0.0254 メートル) しかないにもかかわらず、2 つの別々のクラスに配置されます。 この差の関係は、グループの別のメンバーが 5 フィート 1 インチ (1.5494 メートル)、2 人目のメンバーが 6 フィート 6 インチ (1.9812 メートル) の場合でも同様です。 分類が粗いため、身長間の関係を完全に把握することができません。
さまざまな人々の身長の関係をより適切に表現するには、クラスをさらに追加します。 たとえば、クラスをさらに 2 つ追加します。低は 4 フィート 10 インチ (1.4732 メートル) 以下、中の低は 4 フィート 10 インチ (1.4732 メートル) ~ 5 フィート 4 インチ (1.6256 メートル)、中は 5 フィート 4 インチ (1.6256 メートル) 〜 5 フィート 10 インチ (1.778 メートル)、中の高は 5 フィート 10 インチ (1.778 メートル) 〜 6 フィート 4 インチ (1.9304 メートル)、高は 6 フィート 4 インチ (1.9304 メートル) より大きいとします。 このようにクラスを調整することで、人々の身長の関係をより正確に把握できます。
さらにクラスを追加して、詳細に調整することもできます。 ただし、追加したクラスの数にかかわらず、人々の身長の関係は一般化されます。 厳密に定義されたクラスに分類できない現象もあります。 現実世界を個別のクラスにグループ化することが困難な場合があります。
これまで説明したように、クラスの境界を定義することは主観的であり、現象の定義によって変化する可能性があります。 上記の定義された身長クラスでは、人々は成人であり、ほとんどの場合は男女の混合であることを前提としています。 グループが完全に女性だけで構成されている場合、クラスの定義を変更する必要があります。 グループが子供だけで構成されている場合や、子供を含む場合は、クラスの境界をさらに変更する必要があります。
クラスの定義と現象の特性によって、モデル化する現象を表現する方法が決まります。 測定誤差により、分類の問題はさらに複雑化します。 人々の身長を計測する手順がプラスマイナス 1 インチ (0.0254 メートル) の正確度である場合、その不正確さによって現象が割り当てられるクラスが変わる可能性があります。
ファジー論理は、分類処理で発生するこのような不正確さをモデル化します。 ファジー論理では、クラスは集合として定義されます。 たとえば、住宅適合性モデルにおける最適な傾斜角値などでは、集合のメンバーシップに最適な値について共通認識があります。 値が最適値から離れるほど明瞭度は下がり、一定の値になるとその値が集合に属さない (例: 建築するには確実に勾配が急すぎる) ことが明らかになります。
たとえば、上記の身長の例で、身長に 3 つのクラス (低、中、高) を使用する場合、ファジー論理では 3 つのクラスを重ね合わせることができます。
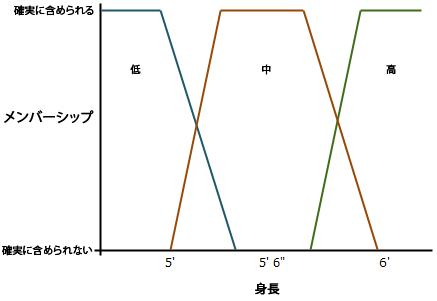
上の画像で、各クラスへのフル メンバーシップは次のとおりです。
- 低: 5 フィート (1.524 メートル) 未満
- 中: 5 フィート 3 1/2 インチ (1.6129 メートル) 〜 5 フィート 8 1/2 インチ (1.7399 メートル)
- 高: 6 フィート (1.8288 メートル) 超
低の集合 (またはクラス) の場合、5 フィート (1.524 メートル) 以下の人々は確実に小の集合に含まれ、1 が割り当てられます。 身長が 5 フィート (1.524 メートル) を超え、5 フィート 3 1/2 インチ (1.6129 メートル) 未満の人々は、小と中の集合 (またはクラス) の間に位置します。 身長が 5 フィート (1.524 メートル) 〜 5 フィート 1 3/4 インチ (1.6193 メートル) の場合は、低の集合に含まれる可能性が高くなります。 身長が 5 フィート 1 3/4 インチ (1.6193 メートル) を超え、5 フィート 3 1/2 インチ (1.6129 メートル) 以下の場合、低の集合に属する可能性もありますが、中の集合に属する可能性のほうが高くなります。
ファジー化処理は、一般的に [ファジー メンバーシップ (Fuzzy Membership)] ツールを使用した、事前に定義された関数によって実行されます。
ファジー メンバーシップ
ファジー化処理は、明確に定義された境界が存在しない現象に対するクラスの不正確さを特徴付けます。
ファジー化では、現象の元の値が、定義された集合に属する可能性に変換されます。 定義された集合は、適合性が高いこと、望ましい距離内であること、指定した鉱物が見つかる可能性があることなどから構成されます。 現象の元の値は、事前に定義されたファジー メンバーシップ関数または他の再分類手法によって、この連続的なメンバーシップ上に再分類されます。
ファジー化処理では、集合へのメンバーシップの理想的な定義が行われます。 集合の中心的な定義により近い現象の場合、各値に対して 1 が割り当てられます。 集合に確実に含まれない値に対しては、0 が割り当てられます。 2 つの極値の間に位置する値は、集合の移行ゾーン (境界) に該当します。 値が最適値または集合の中心から離れるにつれて、1 〜 0 の連続的な評価尺度で減少する値が割り当てられます。 割り当てられた値が減少するにつれて、元の現象値がその集合のメンバーである可能性も低くなります。
ファジー化値 0.5 が交差ポイントです。 0.5 より大きいファジー値は、元の現象値がその集合のメンバーである可能性が高いことを意味します。 ファジー化値が 0.5 を下回ると、元の現象値が集合のメンバーである可能性は低くなり、値が集合に含まれない可能性が高くなります。
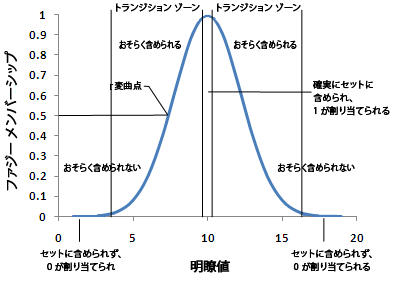
移行ゾーンの幅は、モデル化する現象、現象に付いての情報、集合の定義、計測の正確度によって決まります。 ファジー化関数のパラメーターを変更することで、移行ゾーンの特性を定義できます。 以下の図は、Fuzzy Gaussian 関数と、関数のパラメーターを変更することで生成される 3 つの異なる曲線を示します。
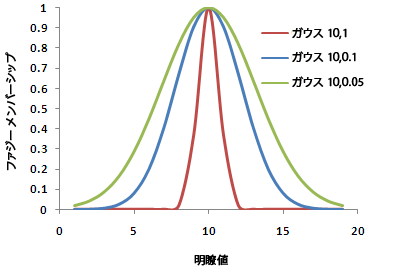
パラメーターは集合を定義する修飾子として機能します。 修飾子は、集合間で発生する可能性がある重複または中間領域を特徴付けます。
ファジー化処理は、オーバーレイ解析の各条件に対して行われます。
ファジー オーバーレイ手法
オーバーレイ モデルで複数の条件に対するすべての集合間の関係と相互作用を解析するには、ファジー オーバーレイ手法を使用します。 ファジー化処理は集合へのメンバーシップ度に基づいているため、オーバーレイ手法は集合のメンバーシップの不正確さによる相互作用について明らかにします。 ファジー オーバーレイ手法は集合論に基づいています。 集合論とは、特定の集合への事象のメンバーシップ関係を定量化する数学的手法です。 ファジー オーバーレイでは、通常、1 つの集合が 1 つのクラスに対応します。
使用可能なファジー集合オーバーレイ手法は、Fuzzy And、Fuzzy Or、Fuzzy Product、Fuzzy Sum、および Fuzzy Gamma です。 これらの各手法は、入力集合に対するセルのメンバーシップ関係を明らかにします。 たとえば、Fuzzy And オーバーレイ タイプを使用すると、各セル値に、セル位置が属する各集合に割り当てられた最小ファジー値を指定する出力ラスターが作成されます。 オーバーレイ解析が住宅適合性モデルで、複数の条件がそれぞれ適切な集合へのメンバーシップに関してファジー化されている場合、Fuzzy And は、セルが複数の条件内で適合する集合のいずれかに属する最小の可能性を特定します。
Fuzzy Or タイプは、集合の交差ポイントの最大値を返します。 つまり、住宅適合性モデルでは、各セルで最大の可能性があるメンバーシップ (最高適合性値) が複数の条件に対して評価されます。
バイナリ、加重、およびファジー論理オーバーレイ
オーバーレイ解析に関するファジー論理の説明の多くは、通常、ファジー論理をバイナリ オーバーレイ解析と比較しています。 バイナリ オーバーレイ解析では、条件ごとに指定したクラスに属しているかどうかに関して、各セルが評価されます。 これまで説明したとおり、多くの場合、明瞭なクラス境界を定義してセルを特定のクラスに確実に割り当てることは困難です。 住宅適合性モデルの場合、バイナリ解析では、条件ごとに各セルに 1 (適合している) または 0 (適合していない) が割り当てられます。 オーバーレイ処理では、すべての入力条件に対して 1 が割り当てられた位置が、適合性が高い可能性がある位置と見なされます。
バイナリ オーバーレイ解析方法には、次のような制限があります。
- すべての条件を満たす位置が存在しない場合、2 番目に適合するオプションは特定されない。
- 条件を満たす位置に対して相対的な加重が行われない。
- 分類処理に関して、上で説明した問題が発生する。
加重オーバーレイ解析は、このような制限に対応するために使用されます。 [加重オーバーレイ (Weighted Overlay)] ツールは、各セルを 1 または 0 の二値の評価尺度で分類するのではなく、定義済みの連続的な評価尺度 (たとえば、1 〜 10 の評価尺度で、10 が条件に対する選好度が最も高い) で各セル値を割り当てます。 連続的な評価尺度を使用すると、クラスの段階的な変化を詳細に表現でき、現象の表現をさらに改善できます。 条件ごとに、各セルに 1 〜 10 の評価尺度が割り当てられます。 次に、再分類された各条件が合算されます。 合計値が最も高いセル位置が、入力条件に対する選好度が最も高い位置となります。 各入力に対して望ましい条件が多いほど、適合性も高くなります。
ファジー オーバーレイと加重オーバーレイの類似性は、それぞれのオーバーレイとバイナリ オーバーレイの類似性よりも高いものの、これらの 2 つのオーバーレイの基礎は異なります。 ファジー オーバーレイは集合論に基づいているのに対し、加重オーバーレイは線形結合に基づいています。 いずれの手法も元の値を変換します。 ファジー オーバーレイでは、変換によって集合へのメンバーシップの可能性が定義されるのに対し、加重オーバーレイは相対的な選好度の評価尺度に基づいています。 これらの 2 つの手法は独自の手法であるため、複数の条件間で解析を実行するツールに互換性はありません。
ファジー論理と一般的なオーバーレイ解析処理
ファジー論理オーバーレイ解析は、一般的なオーバーレイ解析手順に従っているものの、特に一定の手順に重点が置かれており、割り当てられた数値には、他のオーバーレイ解析方法に比べて異なる意味が与えられています。
一般的なオーバーレイ解析手順は次のとおりです。
- 問題の定義
- 問題のサブモデルへの分割
- 重要度の高いレイヤーの決定
- レイヤー内のデータの再分類または変換
- 入力レイヤーへの重み付け
- レイヤーの追加または結合
- 分析
すべてのオーバーレイ解析と同様、ファジー論理解析でも手順 1 〜 3 を実行します。 ファジー論理は集合に基づくため、再分類された値の意味 (手順 4) と、複数の条件を組み合わせて使用できる解析手法 (手順 6) により、ファジー論理は他のオーバーレイ解析方法と比べて独自の手法となっています。
次のセクションでは、手順 4 〜 7 でファジー論理が他の手法と異なる点について説明します。
レイヤー内のデータの再分類または変換
入力データは 0 〜 1 の評価尺度に再分類または変換され、指定した集合に属する可能性を表します。 このような再分類 (ファジー化処理) は、[ファジー メンバーシップ (Fuzzy Membership)] ツールによって実行されます。 この変換処理をサポートするため、一連のメンバーシップ関数が開発されています。 使用可能な関数は、Fuzzy Gaussian、Fuzzy Large、Fuzzy Linear、Fuzzy MSLarge、Fuzzy MSSmall、Fuzzy Near、および Fuzzy Small です。 各メンバーシップ関数は、特定の方法でデータを変換し、現象の相互作用を把握します。
入力レイヤーの重み付け
ファジー論理は集合論に基づいており、特定の位置が 1 つまたは複数の集合に属しているかどうかを決定するものであるため、重み付けを行う意味はありません。 ある要素の加重を別の要素より増やしても、1 つの集合または複数の集合の組み合わせに属する可能性を高めることはできません。 位置は集合のメンバーであるかメンバーでないかのいずれかになります (両者の間のあらゆるメンバーシップ度も含みます)。 ファジー オーバーレイ解析では、条件の重み付けを適用できません。
レイヤーの追加または結合
追加または結合の手順では、ファジー論理は現象が複数の集合に属する可能性の相互作用を調査します。一方、加重オーバーレイと加重合計は、望ましい要素が多いほど適合性が高いという考えに基づいています。
ファジー オーバーレイには、このような相対的関係を調査し、相互作用を定量化する特定の手法があります。 結合には、Fuzzy And、Fuzzy Or、Fuzzy Product、Fuzzy Sum、および Fuzzy Gamma を使用します。 これらの各方法は集合論に基づいており、ファジー オーバーレイ解析固有の方法です。
解析
すべてのオーバーレイ解析で、結果の解析と解釈はユーザーに委ねられています。 ただし、再分類された値にはそれぞれ異なる意味があり、各オーバーレイ方法にはそれぞれ基になるオーバーレイ手法があるため、結果の有効性を計るには別のメカニズムを使用する必要がある場合もあります。