線形回帰は、[AutoML を使用したトレーニング (Train Using AutoML)] ツールで使用される教師付き機械学習手法で、説明変数と従属変数の相関を最もよく表す線形方程式を見つけます。 これは、最小二乗法を使用してデータに直線を適合することで行われます。 この直線は、残差の二乗和を最小化しようとします。 残差は、直線と説明変数の実際の値との間の距離です。 最も適合する直線の特定は反復的なプロセスです。
以下は、結果として得られた線形回帰方程式の例です。
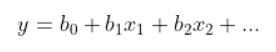
上記の例では、y は従属変数、x1、x2 などは説明変数です。 係数 (b1、b2 など) は、説明変数と従属変数の相関関係を説明します。 係数の符号 (+/-) は、変数が正または負の相関関係にあるかどうかを示します。b0 は、すべての説明変数が 0 であると仮定して、従属変数の値を示す切片です。
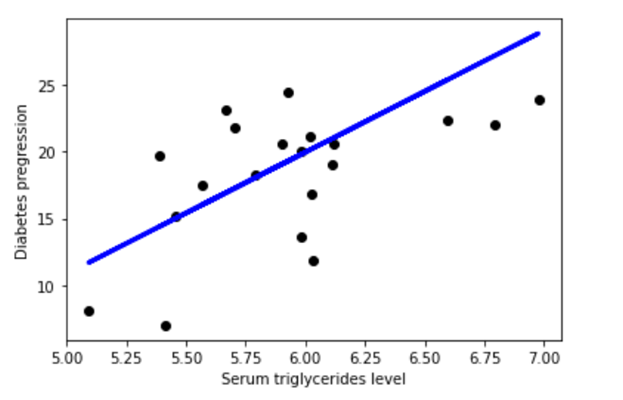
次の画像では、線形回帰モデルは、回帰直線 y = 153.21 + 900.39x で表されます。 モデルは、従属変数である糖尿病の進行と、説明変数である血清トリグリセリドのレベルとの関係を示します。 正の相関が見られます。 この例は、2 つの変数を持つ線形回帰モデルを示しています。 3 つを超える変数を持つモデルを視覚化することはできませんが、実際には、モデルには任意の数の変数を含めることができます。
線形回帰モデルは、従属変数の値の予測に役立ち、予測の精度の説明にも役立ちます。 これは、相関係数の二乗と p 値の値で表されます。 相関係数の二乗の値は、従属変数の変動を説明変数によってどの程度説明できるかを示します。p 値は、説明の信頼度を示します。 相関係数の二乗の値の範囲は 0 ~ 1 です。 値 0.8 は、説明変数が従属変数の観測値の変動の 80% を説明できることを意味します。 値 1 は、完全な予測が可能であることを意味しますが、これは実際にはまれです。 値 0 は、説明変数が従属変数の予測にまったく役立たないことを意味します。 p 値を使用すると、従属変数に対する説明変数の影響が 0 と大きく異なるかどうかをテストできます。