


L’analyse de régression calcule la relation estimée entre une variable dépendante et une ou plusieurs variables explicatives. Elle vous permet de modéliser la relation entre les variables choisies et de prévoir des valeurs en fonction du modèle.
Vue d’ensemble de l’analyse de régression
L’analyse de régression utilise une méthode d’estimation choisie, une variable dépendante et une ou plusieurs variables explicatives pour former une équation qui estime les valeurs de la variable dépendante.
Le modèle de régression inclut des sorties, telles que R2 et des valeurs p, pour fournir des informations sur la façon dont le modèle estime la variable dépendante.
Des diagrammes, tels que des matrices de nuages de points, des histogrammes, et des diagrammes à points, peuvent également être utilisés dans l’analyse de régression pour analyser les relations et tester les hypothèses.
L’analyse de régression peut servir à résoudre les types de problèmes suivants :
- Identifier les variables explicatives qui sont associées à la variable dépendante.
- Comprendre la relation entre les variables dépendantes et explicatives.
- Prévoir les valeurs inconnues de la variable dépendante.
Exemples
Un analyste d’une petite chaîne de magasins étudie les performances des différentes implantations des points de vente. Il souhaite savoir pourquoi le volume des ventes de certains points de vente est si bas. L’analyste crée un modèle de régression avec des variables explicatives, telles que l’âge médian et le revenu médian dans le voisinage, ainsi que la distance pour se rendre aux centres commerciaux et les transports en commun, en vue d’identifier les variables qui ont une influence sur les ventes.
Un analyste du ministère de l’éducation étudie les effets des programmes de petit-déjeuner scolaire. Il crée un modèle de régression des résultats scolaires, tels que le taux de réussite aux examens, à l’aide de variables explicatives telles que la taille des classes, le revenu des ménages, le budget scolaire par élève et la proportion d’élèves qui prennent leur petit-déjeuner tous les jours. L’équation du modèle peut servir à déterminer l’effet relatif de chaque variable sur les résultats scolaires.
Un analyste d’un organisme non gouvernemental étudie les émissions mondiales de gaz à effet de serre. Il crée un modèle de régression correspondant aux émissions les plus récentes pour chaque pays à l’aide de variables explicatives, telles que le produit intérieur brut (PIB), la population, la production d’électricité avec des énergies fossiles et l’utilisation des véhicules. Le modèle peut ensuite servir à prévoir les futures émissions de gaz à effet de serre à l’aide des valeurs prévues pour le PIB et la population.
Moindres carrés ordinaires
L’analyse de régression dans ArcGIS Insights est modélisée à l’aide de la méthode des moindres carrés ordinaires.
La méthode des moindres carrés ordinaires est une forme de régression linéaire multiple, c’est-à-dire que la relation entre les variables dépendantes et les variables indépendantes doit être modélisée en appliquant une équation linéaire aux données observées.
Un modèle des moindres carrés ordinaires utilise l’équation suivante :
yi=β0+β1x1+β2x2+...+βnxn+εoù :
- yi = valeur observée de la variable dépendante au point i
- β0 = interception avec l’axe des y (valeur constante)
- βn = coefficient de régression ou pente pour la variable explicative N au point i
- xn = valeur de la variable N au point i
- ε = erreur de l’équation de régression
Hypothèses
Chaque méthode de régression comporte plusieurs hypothèses qui doivent être vérifiées pour que l’équation soit considérée comme fiable. Les hypothèses des moindres carrés ordinaires doivent être validées lors de la création d’un modèle de régression.
Les hypothèses suivantes doivent être testées et vérifiées pour utiliser la méthode des moindres carrés ordinaires :
- Le modèle doit être linéaire
- Les données doivent être échantillonnées de manière aléatoire
- Les variables explicatives ne doivent pas être colinéaires
- Les variables explicatives doivent présenter une erreur de mesure négligeable
- La somme attendue des résiduels est zéro
- La variance des résiduels est homogène
- Les résiduels sont distribués normalement.
- Les résiduels adjacents ne doivent pas présenter d’auto-corrélation
Le modèle doit être linéaire
La régression des moindres carrés ordinaires peut uniquement servir à créer un modèle linéaire. La linéarité peut être testée entre la variable dépendante et les variables explicatives à l’aide d’un nuage de points. Une matrice de nuages de points permet de tester toutes les variables, à condition que leur nombre total ne dépasse pas cinq.
Les données doivent être échantillonnées de manière aléatoire
Les données utilisées dans l’analyse de régression doivent être échantillonnées de façon que les échantillons mêmes ne dépendent pas d’un facteur externe. L’échantillonnage aléatoire peut être testé à l’aide des résiduels du modèle de régression. Les résiduels, qui sont une sortie du modèle de régression, ne doivent présenter aucune corrélation lorsqu’ils sont tracés avec les variables explicatives sur un nuage de points ou une matrice de nuages de points.
Les variables explicatives ne doivent pas être colinéaires
La colinéarité désigne une relation linéaire entre des variables explicatives, ce qui génère une redondance dans le modèle. Dans certains cas, le modèle peut être créé avec une colinéarité. Toutefois, si une des variables colinéaires semble dépendre de l’autre, il peut être judicieux de supprimer cette variable du modèle. Vous pouvez tester la colinéarité à l’aide d’un nuages de points ou d’une matrice de nuages de points des variables explicatives.
Les variables explicatives doivent présenter une erreur de mesure négligeable
L’exactitude d’un modèle de régression est limité à celle de ses données en entrée. Si les variables explicatives présentent des marges d’erreur importantes, le modèle ne peut pas être accepté comme exact. Lorsque vous effectuez une analyse de régression, il est important d’utiliser uniquement des jeux de données issus de sources connues et fiables pour vous assurer que le taux d’erreur est négligeable.
La somme des résiduels est de zéro
Les résiduels correspondent à la différence entre valeurs observées et estimées dans une analyse de régression. Les valeurs observées situées au-dessus de la courbe de régression ont une valeur résiduelle positive et les valeurs observées situées au-dessous de la courbe de régression ont une valeur résiduelle négative. La courbe de régression doit reposer le long du centre des points de données. Par conséquent, la somme des résiduels doit être égale à zéro. La somme d’un champ peut être calculée dans une table de synthèse.
La variance des résiduels est homogène
La variance doit être la même pour tous les résiduels. Cette hypothèse peut être testée à l’aide d’un nuage de points des résiduels (axe des y) et des valeurs estimées (axe des x). Le nuage de points généré doit s’afficher sous forme de bande horizontale de points tracés de manière aléatoire à travers l’ensemble du tracé.
La distribution des résiduels est normale
Une distribution normale, également nommée courbe en forme de cloche, est une distribution qui se produit naturellement, où la fréquence d’un phénomène est élevée à proximité de la moyenne et se réduit à mesure qu’il s’éloigne de la moyenne. Une distribution normale est souvent utilisée comme hypothèse nulle dans une analyse statistique. Les résiduels doivent être distribués normalement pour montrer que la ligne d’ajustement est optimisée de façon centrale parmi les points de données observés, et non penchés vers certains et éloignés d’autres. Cette hypothèse peut être testée en créant un histogramme avec les résiduels. La courbe de distribution normale peut être superposée et les mesures d’inclinaison et d’aplatissement sont indiquées au bas de la fiche d’histogramme.
Les résiduels adjacents ne doivent pas présenter d’auto-corrélation
Cette hypothèse repose sur des données classées chronologiquement. Si les données sont classées chronologiquement, chaque point de données doit être indépendant du point de données précédent ou suivant. Il est par conséquent important de s’assurer que les données classées chronologiquement sont organisées dans l’ordre approprié lorsque vous effectuez une analyse de régression. Cette hypothèse peut être calculée à l’aide du test de Durbin-Watson.
Le test de Durbin-Watson mesure l’auto-corrélation des résiduels dans un modèle de régression. Le test de Durbin-Watson utilise une échelle de 0 à 4, les valeurs comprises entre 0 et 2 indiquant une auto-corrélation positive, 2 indiquant l’absence d’auto-corrélation et les valeurs comprises entre 2 et 4 indiquant une auto-corrélation négative. Par conséquent, les valeurs proches de 2 sont nécessaires pour satisfaire à l’hypothèse d’une absence d’auto-corrélation des résiduels. En général, les valeurs comprises entre 1,5 et 2,5 sont considérées acceptables, tandis que les valeurs inférieures à 1,5 ou supérieures à 2,5 indiquent que le modèle ne satisfait pas à l’hypothèse ne non corrélation.
Validité du modèle
L’exactitude d’une équation de régression joue un rôle important dans l’analyse de régression. Tous les modèles incluent une certaine marge d’erreur, mais comprendre les statistiques vous permettra de déterminer si le modèle peut être utilisé dans votre analyse ou si des ajustements doivent être apportés.
Deux techniques permettent de déterminer la validité d’un modèle de régression : l’analyse exploratoire et l’analyse de confirmation.
Analyse exploratoire
L'analyse exploratoire utilise un ensemble de techniques visuelles et statistiques pour vous permettre de comprendre vos données. Au cours de votre analyse exploratoire, vous allez tester les hypothèses d’une régression par les moindres carrés ordinaires et comparer l’efficacité des différentes variables explicatives. L'analyse exploratoire vous permet de comparer l’efficacité et la précision de différents modèles, mais pas de déterminer si votre modèle peut être utilisé ou s’il doit être rejeté. L'analyse exploratoire doit être effectuée avant l’analyse de confirmation pour chaque modèle de régression et répétée pour comparer des modèles.
Les diagrammes et statistiques suivants peuvent être utilisés dans le cadre d’une analyse exploratoire :
- Nuage de points et matrice de nuages de points
- Histogramme et distribution normale
- Équation de régression et prévision de nouvelles observations
- Coefficient de détermination, R2 et R2 ajusté
- Erreur résiduelle standard
- Diagramme à points
L’analyse exploratoire doit débuter au moment du choix des variables explicatives et avant de créer un modèle de régression. La méthode des moindres carrés ordinaires étant une méthode de régression linéaire, l’une des hypothèses principales est que le modèle doit être linéaire. Un nuage de points ou une matrice de nuages de points peuvent permettre d’évaluer la linéarité entre la variable dépendante et les variables explicatives. Une matrice de nuages de points peut afficher jusqu’à quatre variables explicatives avec la variable dépendante, ce qui en fait un outil important pour effectuer des comparaisons à grande échelle entre toutes les variables. Un nuage de points unique n'affiche que deux variables : une variable dépendante et une variable indépendante ou explicative. Afficher un nuage de points de la variable dépendante et d’une seule variable explicative vous permet d’évaluer avec une plus grande précision la relation existante entre les variables. La linéarité peut être testée avant de créer un modèle de régression pour vous aider à déterminer quelles variables explicatives formeront un modèle acceptable.
Plusieurs sorties statistiques sont disponibles une fois le modèle de régression créé, ce qui inclut l’équation de régression, la valeur R2, et le test de Durbin-Watson. Une fois que vous avez créé un modèle de régression, vous devez utiliser les sorties et diagrammes requis pour tester les hypothèses restantes de régression par les moindres carrés ordinaires. Si votre modèle confirme les hypothèses, vous pouvez poursuivre l’analyse exploratoire.
L’équation de régression fournit des informations utiles concernant l’influence de chaque variable explicative sur les valeurs de prévision, notamment le coefficient de régression pour chaque variable explicative. Les valeurs de pente peuvent être comparées pour déterminer l’influence relative de chaque variable explicative sur la variable dépendante ; plus la valeur de pente est éloignée de zéro (que la valeur soit positive ou négative), plus l’influence est grande. L’équation de régression peut également être utilisée pour prévoir des valeurs pour la variable dépendante en saisissant des valeurs pour chaque variable explicative.
Le coefficient de détermination, symbolisé par R2, mesure la façon dont l’équation de régression modélise les points de données réels. La valeur R2 est un nombre compris entre 0 et 1, les valeurs les plus proches de 1 indiquant des modèles d’une plus grande exactitude. Une valeur R2 égale à 1 désigne un modèle parfait, ce qui est hautement improbable dans des situations réelles, étant donné la complexité des interactions entre différents facteurs et des variables inconnues. Vous devez par conséquent vous efforcer de créer un modèle de régression dont la valeur R2 est la plus élevée possible, tout en acceptant que cette valeur ne soit pas proche de 1.
Lorsque vous réalisez une analyse de régression, vous risquez de créer par pur hasard un modèle de régression dont la valeur R2 est acceptable en ajoutant des variables explicatives qui déclenchent une meilleure adéquation. La valeur R2 ajustée, qui est également comprise entre 0 et 1, tient compte des variables explicatives supplémentaires, ce qui atténue le rôle que joue le hasard dans le calcul. La valeur R2 ajustée doit être utilisée pour les modèles qui utilisent de nombreuses variables explicatives ou pour comparer des modèles comportant différents nombres de variables explicatives.
L’erreur résiduelle standard mesure la précision avec laquelle le modèle de régression peut prévoir les valeurs avec de nouvelles données. Les valeurs plus faibles indiquent un modèle plus précis ; lorsque plusieurs modèles sont comparés, le modèle ayant la valeur la plus faible sera celui réduisant au minimum l’erreur résiduelle standard.
Les diagrammes à points peuvent être utilisés pour analyser vos variables explicatives pour les modèles tels que l’agrégation et les points aberrants, qui peuvent affecter la précision du modèle.
Analyse de confirmation
L’analyse de confirmation est le processus qui consiste à tester votre modèle par rapport à une hypothèse nulle. Dans une analyse de régression, l’hypothèse nulle signifie qu’il n’existe aucune relation entre la variable dépendante et les variables explicatives. Les valeurs de pente d’un modèle sans relation seraient égales à 0. Si les éléments de votre analyse de confirmation sont statistiquement pertinents, vous pouvez écarter l’hypothèse nulle (en d’autres termes, la pertinence statistique indique qu’il existe une relation entre les variables dépendante et explicatives).
Les sorties statistiques suivantes sont utilisées pour déterminer la pertinence dans le cadre de l’analyse de confirmation :
- Statistique F et sa valeur p associée
- Statistiques t et leurs valeurs p associées
- Intervalles de confiance
La statistique F est une statistique globale renvoyée par un test F, qui indique la capacité de prévision du modèle de régression en déterminant si tous les coefficients de régression du modèle sont significativement différents de 0. Le test F analyse l’influence combinée des variables explicatives, plutôt que de les tester individuellement. La statistique F est associée à une valeur p, qui indique la probabilité que les relations dans vos données soient le fruit du hasard. Puisque les valeurs p reposent sur les probabilités, les valeurs sont données sur une échelle allant de 0,0 à 1,0. Une valeur p basse, en général 0,05 ou moins, est requise pour déterminer que les relations du modèle sont réelles (c’est-à-dire, qu’elles ne sont pas le fruit du hasard) et pour écarter l’hypothèse nulle. Dans ce cas, la probabilité que les relations du modèle soient le fruit du hasard est de 0,05, soit 1 sur 20. Autrement dit, la probabilité que les relations du modèle soient réelles est de 0,95, soit 19 sur 20.
La statistique t est une statistique locale renvoyée par un test t, qui indique la capacité de prévision de chaque variable explicative individuellement. Comme le test F, le test t analyse si les coefficients de régression du modèle sont significativement différents de zéro. Toutefois, puisque le test t est effectué sur chaque variable explicative, le modèle renvoie une valeur statistique t pour chaque variable explicative, au lieu d’une par modèle. Chaque statistique t est associée à une valeur p, qui indique la pertinence de la variable explicative. Comme pour les valeurs p du test F, la valeur p de chaque test t doit être inférieure ou égale à 0,05 pour écarter l’hypothèse nulle. Si la valeur p d’une variable est supérieure à 0,05, la variable doit être écartée et un nouveau modèle créé, même si la valeur p globale était significative.
Les intervalles de confiance montrent le coefficient de régression pour chaque variable explicative et les intervalles de confiance de 90, 95 et 99 pour cent associés. Les intervalles de confiance peuvent par conséquent être utilisés avec les valeurs p provenant des tests t pour évaluer l’hypothèse nulle en ce qui concerne les variables explicatives individuelles. Les coefficients de régression ne doivent pas être égaux à 0 pour pouvoir écarter l'hypothèse nulle et continuer à utiliser le modèle. Par conséquent, pour chaque variable explicative, le coefficient de régression et les intervalles de confiance associés ne doivent pas inclure la valeur 0. Si un intervalle de confiance de 99 ou 95 pour cent pour une variable explicative donnée inclut la valeur 0, la variable explicative n’a pas réussi à écarter l’hypothèse nulle. Le fait d’inclure une telle variable peut avoir un impact sur la pertinence globale de votre modèle. Si seul l’intervalle de confiance de 90 pour cent contient la valeur 0, la variable explicative peut être incluse dans le modèle à condition que les autres statistiques globales soient pertinentes. Idéalement, les intervalles de confiance de toutes les variables explicatives doivent être éloignés de 0.
Autres sorties
D’autres sorties, comme les valeurs estimées et les résiduels, sont importantes pour valider les hypothèses de régression par les moindres carrés ordinaires. Dans cette section, vous approfondirez vos connaissances sur la façon dont ces valeurs sont calculées.
Valeurs estimées
Les valeurs estimées sont calculées à l’aide de l’équation de régression et des valeurs de chaque variable explicative. Idéalement, les valeurs estimées seront égales aux valeurs observées (c’est-à-dire aux valeurs réelles de la variable dépendante).
Les valeurs estimées sont utilisées avec les valeurs observées pour calculer les résiduels.
Résiduels
Les valeurs résiduelles dans une analyse de régression correspondent aux différences entre les valeurs observées dans le jeu de données et les valeurs estimées calculées avec l’équation de régression.
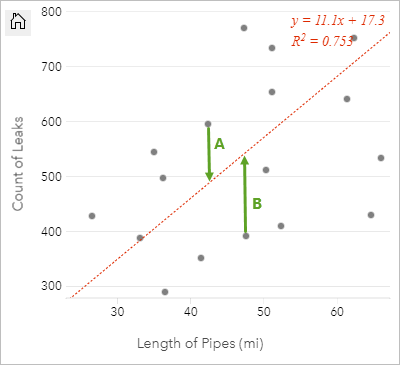
Les résiduels A et B de la relation ci-dessus sont calculés comme suit :
residualsA = observedA - estimatedA residualsA = 595 - 487.62 residualsA = 107.38residualsB = observedB - estimatedB residualsB = 392 - 527.27 residualsB = -135.27Les résiduels peuvent servir à calculer la marge d’erreur dans une équation de régression et à tester plusieurs hypothèses.
Vous avez un commentaire à formuler concernant cette rubrique ?