L’outil Distances moyennes du plus proche voisin mesure la distance entre le centroïde de chaque entité et le centroïde de son voisin le plus proche. Il fait ensuite la moyenne de toutes ces distances par rapport au voisin le plus proche. Si la distance moyenne est inférieure à la moyenne d’une distribution aléatoire hypothétique, la distribution des entités en cours d’analyse est considérée comme agrégée. Si la distance moyenne est supérieure à une distance aléatoire hypothétique, les entités sont considérées comme dispersées. Le ratio moyen du voisin le plus proche correspond à la distance moyenne observée divisée par la distance moyenne attendue (avec la distance moyenne attendue basée sur une distribution aléatoire hypothétique avec le même nombre d’entités couvrant la même zone totale).
Calculs

Interprétation
Si l’indice (ratio moyen du voisin le plus proche) est inférieur à 1, le modèle présente un phénomène d’agrégation. Si l’indice est supérieur à 1, la tendance est à la dispersion.
Les équations utilisées pour calculer l’indice de distances moyennes du plus proche voisin (1) et le score z (4) se basent sur l’hypothèse que les points à mesurer peuvent se trouver n’importe où dans la zone d’étude (il n’y a par exemple aucune interruption et tous les cas ou entités sont positionnés de manière indépendante les uns des autres). La valeur p est une approximation numérique de la surface sous la courbe pour une distribution connue, limitées par la statistique de test. Reportez-vous à la rubrique Qu’est-ce qu’un score z ? Qu’est-ce qu’une valeur p ? pour plus d’informations sur ces statistiques.
Attention :
Le score z et la valeur p pour cette statistique sont sensibles aux modifications de la zone d’étude ou du paramètre Zone. C’est pourquoi vous devez comparer les résultats du score z et de la valeur p de cette statistique uniquement lorsque la zone d’étude est fixe.
Sortie
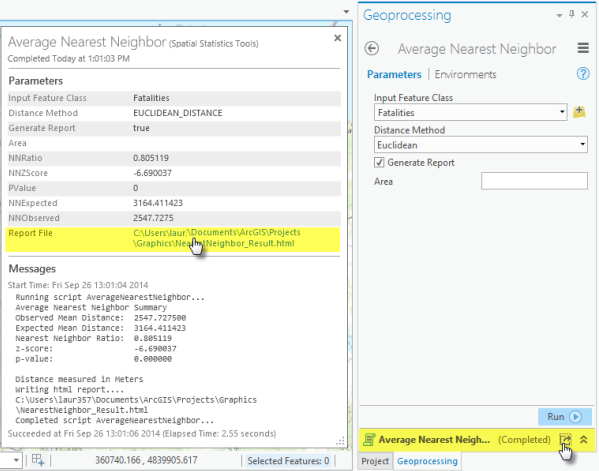
L'outil Distances moyennes du plus proche voisin renvoie cinq valeurs : distance moyenne observée, distance moyenne attendue, indice de voisin le plus proche, score z et valeur p. Les valeurs sont écrites sous forme de messages au bas de la fenêtre Géotraitement au cours de l'exécution de l'outil et transmises sous la forme de valeurs en sortie dérivées pour une utilisation éventuelle dans des modèles ou des scripts. Vous pouvez accéder aux messages en pointant sur la barre de progression, en cliquant sur le bouton contextuel ou en développant la section des messages dans la fenêtre Géotraitement. Vous pouvez également accéder aux messages d'un outil précédemment exécuté via l'historique du géotraitement. Cet outil peut également créer un fichier de rapport HTML contenant un récapitulatif graphique des résultats. Le chemin d'accès au rapport est inclus avec les messages qui récapitulent les paramètres d'exécution de l'outil. Cliquez sur ce chemin d'accès pour ouvrir le fichier de rapport.
Applications possibles
- Évaluer la concurrence ou le territoire : quantifier et comparer la distribution spatiale d’une variété de plante ou d’une espèce animale dans une zone d’étude fixe ; comparer les distances moyennes du plus proche voisin pour différents types d’entreprises dans une ville.
- Suivre l’évolution au fil du temps : évaluer les changements dans l’agrégation spatiale pour un seul type d’entreprise dans une zone d’étude fixe au fil du temps.
- Comparer une distribution observée par rapport à une distribution contrôlée : dans une analyse portant sur le bois, vous voudrez peut-être comparer le modèle des zones exploitées au modèle des zones exploitables afin de déterminer si les zones de coupe sont davantage agrégées que ce qui est attendu, en raison de la distribution globale du bois exploitable.
Ressources supplémentaires
Les ouvrages suivants présentent des informations supplémentaires concernant cet outil :
Ebdon, David. Statistics in Geography. Blackwell, 1985.
Mitchell, Andy. The ESRI Guide to GIS Analysis, Volume 2. ESRI Press, 2005.
Vous avez un commentaire à formuler concernant cette rubrique ?