Comprendre l’analyse de la densité

L’analyse de densité sélectionne des quantités connues de certains phénomènes et les répartit sur le territoire selon la quantité mesurée à chaque localisation et la relation spatiale des localisations des quantités mesurées.

Surface de densité

Les surfaces de densité indiquent les endroits où les entités ponctuelles ou linéaires sont concentrées. Supposons, par exemple, que vous avez une valeur de point, pour chaque localité, représentant le nombre total d’habitants, mais que vous voulez déterminer la répartition de la population dans la région. Étant donné que les habitants de chaque localité ne résident pas au point de population, en calculant la densité, vous pouvez créer une surface représentant la répartition prédite de la population pour tout le territoire.

L’image suivante est un exemple de surface de densité. Lorsqu’elles sont additionnées, les valeurs de population des cellules sont égales à la population totale de la couche de points d’origine.

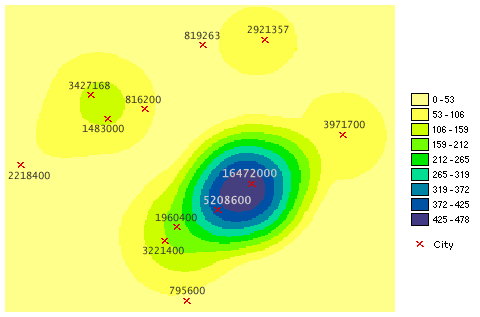
Applications de l’analyse de la densité

Les outils de densité répartissent une quantité mesurée d’une couche de points en entrée sur l’ensemble d’un territoire de manière à générer une surface continue.

Exemple : une chaîne de points de vente répartis dans une zone géographique donnée. Dans chacun des magasins, la direction fixe un chiffre d’affaires. La direction part du principe que les clients préfèrent un magasin à un autre, en fonction du trajet à parcourir. Dans cet exemple, nous supposons que le client choisit toujours le magasin le plus proche. Plus un client est éloigné du magasin le plus proche, plus la distance qu’il doit parcourir est grande. Toutefois, les clients les plus éloignés font également leurs courses dans les autres magasins. La direction souhaite étudier la répartition des lieux de résidence des clients. À l’aide du chiffre d’affaires et de la répartition spatiale des magasins, la direction souhaite générer une surface des clients en les répartissant intelligemment sur l’ensemble du territoire.

Pour y parvenir, l’outil de densité détermine la localisation de chacun des magasins par rapport aux autres, la quantité de clients fréquentant chaque magasin et le nombre de cellules qui devront partager une partie de cette quantité mesurée (les clients). Les cellules plus proches des points mesurés (les magasins) reçoivent des proportions plus élevées de la quantité mesurée que ceux qui sont plus éloignés.