Fonctionnement de l’outil Reliefs de type Géomorphon

La compréhension des diverses caractéristiques du MNT est indispensable pour un large éventail d’applications, des études hydrologiques aux évaluations des risques de glissement de terrain. L’une de ces applications consiste à classer le MNT en reliefs. Un relief est la forme naturelle du MNT, comme les vallées ou les sommets.

Parmi les différentes techniques de classification du MNT figure la méthode des Géomorphons (Jasiewicz et Stepiski, 2013) qui identifie les reliefs en fonction des données du MNT en utilisant les différences d’élévation et les concepts de visibilité. L’outil Reliefs de type Géomorphon applique ces concepts pour identifier un motif distinct qui représente une zone du MNT.

La méthode des Géomorphons peut identifier un total de 498 motifs uniques. Certains géomorphons décrivent les reliefs invisibles dans l’environnement naturel, tandis que d’autres décrivent le même type de relief. Il existe donc une relation plusieurs vers un entre les géomorphons et les types de reliefs. Une fois le géomorphon identifié, il peut être associé à un relief à l’aide d’une table de correspondance.

Logique de l’outil Reliefs de type Géomorphon

L’outil Reliefs de type Géomorphon utilise la méthode des Géomorphons pour classer le MNT en reliefs.

Pour chaque cellule du raster en entrée, l’outil effectue les opérations suivantes :

1. Configuration de la zone d’analyse. Cette opération permet de déterminer la zone d’analyse avec les paramètres Distance de recherche et Distance omise.
2. Obtention du géomorphon à l’aide du motif ternaire local (Local Ternary Pattern, LTP). Pour déterminer le motif ternaire local (LTP) de chacun des 8 points cardinaux, prolongez une ligne de visée et classez-la en fonction de l’angle du nadir et de l’angle zénithal.
3. Transformez le motif ternaire local en nombre de base 3 qui enregistre le motif unique ou géomorphon. Stockage de cette valeur pour la cellule cible.
4. Associez le géomorphon à l’un des 10 reliefs les plus courants à l’aide d’une table de correspondance.

Chacune de ces étapes est expliquée plus en détails dans les sections ci-dessous.

Configurer la zone d’analyse pour calculer le géomorphon

La zone d’analyse de l’outil est la zone de MNT utilisée pour calculer le géomorphon d’une cellule cible. Elle définit les cellules voisines utilisées par l’outil pour déterminer le géomorphon.

La zone d’analyse est déterminée par les paramètres Distance de recherche et Distance omise. Le paramètre Distance de recherche indique l’étendue de la zone couverte. Le paramètre Distance omise identifie la zone des environs immédiats de la cellule cible à exclure de la classification. L’illustration suivante montre un exemple de la zone d’analyse définie par une distance de recherche de trois cellules et une distance omise d’une cellule. Les cellules incluses pour le traitement sont déterminées en comparant la distance entre chaque centre de cellule et la cellule cible à la valeur de la distance de recherche. Si la valeur de la distance de recherche est supérieure, la cellule est incluse pour le traitement.

Figure 1. La zone d’analyse est définie par les distances de recherche et omise mesurées à partir de la cellule cible. a) La cellule cible est identifiée. b) Les distances de recherche et omise sont mesurées à partir de la cellule cible. c) Zone d’analyse obtenue.

La spécification de valeurs de distance de recherche plus élevées risque d’entraîner la généralisation du MNT environnant. Des valeurs plus faibles capturent davantage de détails dans le résultat. Il peut être utile d’augmenter la valeur de la distance omise pour réduire le bruit des cellules proches susceptibles de représenter des valeurs d’élévation erronées ou qui risquent de ne pas fournir d’informations supplémentaires en termes de différence d’élévation.

Ces deux paramètres peuvent également faciliter l’identification des entités de MNT en fonction de leur taille. Pour ce faire, ajustez ces paramètres en leur attribuant des valeurs qui représentent ce que vous cherchez à classer. Vous trouverez ci-après quelques indications générales sur la définition de ces paramètres :

• Utilisez 50 à 100 fois la taille de cellule en entrée pour le paramètre Distance de recherche pour identifier les entités de MNT longues ou larges, comme les rivières. L’identification de telles entités de MNT entraîne également l’identification des petites entités, mais il se peut qu’elles ne soient pas identifiées en fonction de la valeur du paramètre Distance omise. C’est pourquoi, il est recommandé de modifier un paramètre à la fois afin de trouver sa valeur optimale.
• Utilisez 5 à 15 fois la taille de cellule en entrée pour identifier les entités de MNT petites ou étroites, comme les cours d’eau étroits.
• Indiquez des valeurs moins élevées pour identifier les entités de MNT très étroites, comme les lignes de crête.

Obtenir le géomorphon

Une fois la zone d’analyse définie, vous devez calculer le géomorphon en fonction du motif ternaire local (LTP).

Déterminer le motif ternaire local à l’aide de l’angle zénithal et l’angle du nadir

Tout d’abord, le motif ternaire local (LTP) équivaut à attribuer une valeur 0, 1 ou –1 à chacun des 8 points cadinaux. La valeur attribuée à une direction donnée est déterminée par la différence entre l’angle zénithal et l’angle du nadir.

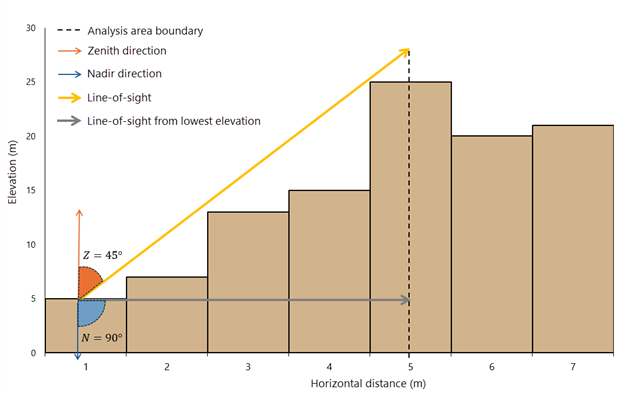
L’angle zénithal, Z, correspond à l’angle formé entre la direction du zénith (directement au-dessus) et la ligne de visée prolongée jusqu’à la limite de la zone d’analyse le long de la direction analysée. Cette ligne représente tout ce qui est visible à partir de la cellule cible.

L’angle du nadir, N, est défini de manière similaire. Il correspond à l’angle formé entre la direction du nadir (directement au sol) et une ligne de visée hypothétique suivant l’élévation la plus basse de la zone jusqu’à la limite de la zone d’analyse.

La Figure 2 représente le profil d’élévations du MNT analysé dans une direction (par exemple, le nord) et chacun des angles définis avec leur ligne de visée respective.

Figure 2. Profil d’élévation vers l’un des points cardinaux à partir de la cellule cible. La ligne de visée et la ligne de visée hypothétiques s’étendent de la cellule cible jusqu’à la limite de la zone d’analyse. Ces lignes, avec les directions du zénith et du nadir, permettent de définir les angles utilisés dans les étapes suivantes de l’algorithme.

Une fois les deux angles déterminés, le seuil de l’angle de MNT plat est utilisé pour déterminer la valeur LTP à attribuer à la direction analysée. L’expression mathématique est la suivante :

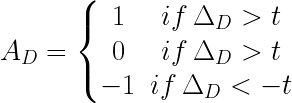
où,

• A_D est la valeur attribuée à la direction analysée ;
• Δ_D est la différence entre l’angle du nadir et l’angle zénithal, Z et N ;
• t est la valeur de seuil d’angle de MNT plat.

Le seuil d’angle de MNT plat est une valeur qui permet de définir une limite sur le MNT qui sera classé comme plat. Dans le cas de l’exemple de la Figure 2, si vous spécifiez 1 (t = 1 degré) pour le seuil d’angle de MNT plat, une valeur 1 est attribuée à la direction analysée. En effet, 90° - 45° = 45° > 1°.

Le même processus est répété dans le sens des aiguilles d’une montre pour chaque point cardinal.

Construction du géomorphon pour chaque cellule cible

Après l’attribution d’une valeur à chacune des 8 directions, le résultat est concaténé en un octuple (8 éléments) qui est stocké dans la cellule cible. (0, -1, 0, 1, 0, 0, 1, 1) est un exemple d’octuple. Pour faciliter le stockage, le tuple est transformé en un nombre ternaire (base 3). Ce résultat correspond au géomorphon.

Il existe is 6561 (3⁸) géomorphons possibles. Bon nombre d’entre eux étant le résultat de la rotation ou de la réflexion d’autres motifs, il est possible de réduire le nombre total de géomorphons à 498.

Associer le géomorphon au type de relief

L’outil utilise la table de correspondance pour associer un géomorphon à un type de relief spécifique, en fonction des arguments présentés par Jasiewicz et Stepinski (2013). La table fait correspondre un géomorphon à l’un des 10 reliefs les plus courants.

Figure 3. Dix types de reliefs les plus courants.

Il est possible d’associer plusieurs géomorphons différents à un relief spécifique si leur définition ne comporte que peu de variations. La variation acceptable est une supposition nécessaire pour créer la table de correspondance.

Figure 4. Table de correspondance permettant d’associer un géomorphon à l’un des 10 types de reliefs les plus courants. Chaque axe indique le nombre total de valeurs (1) ou (-1) présentes dans le modèle.

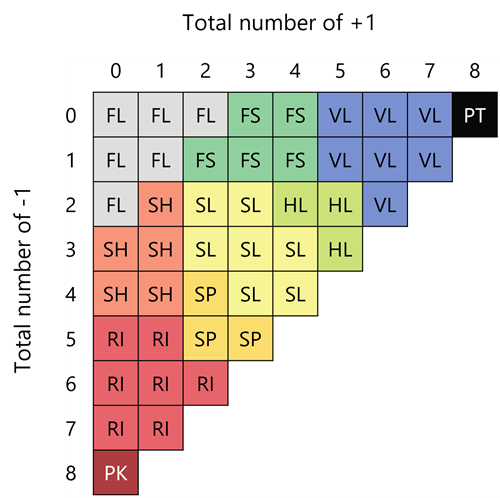
Seuls les reliefs de type Pic et Dépression sont associés à un géomorphon unique. Dans le cas du relief de type Pic (-1, -1, -1, -1, -1, -1, -1, -1), toutes les cellules qui entourent la cellule cible sont plus basses. De même pour le relief de type Dépression (1, 1, 1, 1, 1, 1, 1, 1), toutes les cellules qui entourent la cellule cible sont plus élevées.

Résultats finaux du raster de reliefs et de géomorphons

L’étape finale consiste à stocker le résultat de la mise en correspondance dans la valeur du paramètre Raster de reliefs en sortie. Le géomorphon est une sortie facultative qui peut être utilisée lors d’une analyse ou d’un diagnostic ultérieur.

Bibliographie

Jasiewicz, Juroslav et Tomasz F. Stepinski. 2013. "Geomorphons - a pattern recognition approach to classification and mapping of landforms." Geomorphology Volume 182, 15 janvier, pp. 147–56. https://doi.org/10.1016/j.geomorph.2012.11.005