Estimer la tendance pour chaque pixel selon une dimension pour une ou plusieurs variables d’un raster multidimensionnel.
Remarques
Parmi les jeux de données raster multidimensionnel pris en charge se trouvent le format Cloud Raster Format (CRF), les mosaïques multidimensionnelles ou les couches raster multidimensionnelles générées par des fichiers au format netCDF, GRIB ou HDF.
Cet outil permet d’ajuster les données sur une courbe de tendance linéaire, harmonique ou polynomiale ou de détecter la tendance au moyen du test de Mann-Kendall ou Kendall saisonnier.
Le raster de tendance en sortie généré avec cette fonction sert en entrée pour la fonction Predict Using Trend (Prévoir à l’aide d’une tendance).
Les tests de Mann-Kendall et Kendall saisonnier déterminent si les données présentent une tendance monotonique. Ils ne sont pas paramétriques, c’est-à-dire qu’ils ne formulent aucune hypothèse sur la distribution spécifique des données. Le test de Mann-Kendall ne considère pas une corrélation sérielle ou des effets saisonniers. Si les données ont une saisonnalité, le test de Kendall saisonnier est plus adapté.
Si l’outil réalise le test de Mann-Kendall ou Kendall saisonnier, la sortie est un raster à cinq canaux de type suivant :
- Canal 1 = Pente de Sen
- Canal 2 = Valeur de p
- Canal 3 = Score de Mann-Kendall (S)
- Canal 4 = Variance S
- Canal 5 = Score z
Les sorties des tests de Mann-Kendall ou Kendall saisonnier permettent de déterminer les pixels de votre série temporelle multidimensionnelle qui présentent une tendance statistiquement significative. Vous pouvez utiliser cette information avec une analyse de tendance linéaire, harmonique ou polynomiale pour extraire les tendances significatives de vos séries temporelles. Vous générez un masque comportant les pixels avec une valeur de p significative, appliquez le masque au raster multidimensionnel et utilisez ce raster multidimensionnel masqué comme entrée de l’outil pour effectuer une analyse de tendance linéaire, harmonique ou polynomiale.
Trois options de ligne de tendance permettent d’ajuster une tendance aux valeurs de variable le long d’une dimension : linéaire, polynomiale et harmonique. Ces trois options d’ajustement de tendance sont décrites ci-après.

Pour l’analyse de tendance linéaire, la sortie est un raster à trois canaux du type suivant :
- Canal 1 = Pente
- Canal 2 = Ordonnée à l’origine
- Canal 3 = Racine carrée de l'erreur quadratique moyenne (EQM) ou erreur autour de la ligne de compromis
Pour l’analyse de tendance polynomiale, le nombre de canaux dans la sortie dépend du degré polynomial. Un ajustement polynomial du deuxième degré génère un raster à quatre canaux de type suivant :
- Canal 1 = Polynomial_2
- Canal 2 = Polynomial_1
- Canal 3 = Polynomial_0
- Canal 4 = EQM
Un ajustement polynomial du troisième degré génère un raster à cinq canaux de type suivant :
- Canal 1 = Polynomial_3
- Canal 2 = Polynomial_2
- Canal 3 = Polynomial_1
- Canal 4 = Polynomial_0
- Canal 5 = EQM
Pour l’analyse de tendance harmonique, le nombre de canaux dans la sortie dépend de la fréquence harmonique. Si la fréquence est définie sur 1, la sortie est un raster à cinq canaux de type suivant :
- Canal 1 = Pente
- Canal 2 = Ordonnée à l’origine
- Canal 3 = Harmonic_sin1
- Canal 4 = Harmonic_cos1
- Canal 5 = EQM
Si la fréquence est définie sur 2, la sortie est un raster à sept canaux de type suivant :
- Canal 1 = Pente
- Canal 2 = Ordonnée à l’origine
- Canal 3 = Harmonic_sin1
- Canal 4 = Harmonic_cos1
- Canal 5 = Harmonic_sin2
- Canal 6 = Harmonic_cos2
- Canal 7 = EQM
Le paramètre Length of Cycle (Durée du cycle) pour l’analyse des tendances harmoniques est utilisé pour indiquer le nombre et la durée des cycles que vous vous attendez à voir dans vos données tout au long d’une journée ou d’une année. Si, par exemple, vous prévoyez que vos données connaissent deux cycles de variation dans l’année, la durée du cycle sera de 182,5 jours, soit 0,5 an. Si vos données de température sont recueillies toutes les trois heures, et s’il y a un cycle de variation par jour, la durée du cycle est d’une journée.
Le paramètre Frequency (Fréquence) pour l’analyse des tendances harmoniques est utilisé pour décrire le modèle harmonique à ajuster aux données. Si la fréquence est définie sur 1, une combinaison de tendance linéaire et de courbe harmonique de premier degré est utilisée pour ajuster le modèle. Si la fréquence est définie sur 2, une combinaison de tendance linéaire, de courbe harmonique de premier degré linéaire et de courbe harmonique de second degré est utilisée pour ajuster les données. Si la fréquence est 3, une courbe harmonique de troisième degré supplémentaire est utilisée pour modéliser les données et ainsi de suite.
Des statistiques de la qualité d’ajustement du modèle peuvent être générées en sorties facultatives. L’erreur quadratique moyenne (EQM), la valeur R-carré et la valeur P de pente de la tendance peuvent être calculées et symbolisées. Symbolisez la couche raster de la tendance en sortie à l’aide de la symbologie RGB (RVB) et précisez les statistiques sous la forme de canaux rouge, vert et bleu.
Paramètres
| Paramètre | Description |
|---|---|
Raster | Raster multidimensionnel en entrée. |
Nom de la dimension | Dimension le long de laquelle une tendance sera extraite pour la ou les variables sélectionnées dans l’analyse. |
Type de tendance | Spécifie le type de ligne à utiliser pour ajuster les valeurs de pixel le long d’une dimension.
|
Fréquence harmonique | Numéro de fréquence à utiliser dans l’ajustement de tendance. Ce paramètre spécifie la fréquence des cycles au cours d’une année. La valeur par défaut est de 1, soit un cycle harmonique par an. Ce paramètre n’est inclus dans l’analyse de tendance que pour une régression harmonique. |
Durée du cycle | Durée de la variation périodique à modéliser. L’unité est le jour, quelle que soit l’unité temporelle des données en entrée. Par exemple, la couleur verte des feuilles possède généralement un cycle de variation important au cours d’une année ; la durée du cycle est égale à 365,25, même si les données en entrée font référence à une couleur verte mensuelle. Les données de température par heure affichent souvent un important cycle de variation dans une journée ; aussi la durée du cycle est définie sur 1. La durée par défaut est de 365,25 jours pour les données variant sur un cycle annuel. |
Unité de cycle | Précise l’unité de temps à utiliser pour la durée d’un cycle harmonique.
|
Ordre polynomial | Numéro d’ordre polynomial à utiliser dans l’ajustement de tendance. Ce paramètre spécifie l’ordre polynomial. La valeur par défaut est 2 ou un polynôme de deuxième degré. Ce paramètre n’est inclus dans l’analyse de tendance que pour une régression polynomiale. |
Ignorer NoData | Indique si les valeurs NoData sont ignorées lors de l’analyse.
|
EQM | Indique s’il convient de générer la racine carrée de l’erreur quadratique moyenne (EQM) de la ligne d’ajustement de la tendance.
|
R-carré | Indique s’il convient de calculer la statistique de la qualité de l’ajustement R-carré pour la ligne d’ajustement de la tendance.
|
P-value of Slope Coefficient (Valeur P du coefficient de pente) | Indique s’il convient de calculer la statistique de valeur P du coefficient de pente de la ligne de tendance.
|
Période saisonnière | Spécifie l’unité de temps à utiliser pour mesurer la longueur de la période saisonnière lors du test de Kendall saisonnier
|
Types de régression
L’équation de régression de chaque option de tendance est présentée ci-dessous.
- Linear (Linéaire) : la ligne de tendance linéaire est la ligne droite la mieux adaptée utilisée pour estimer des relations linéaires simples. Une tendance linéaire met en évidence un taux de variation qui augmente ou diminue de manière régulière. La formule de la ligne de tendance linéaire est la suivante :
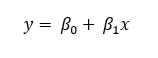
- y = valeur variable du pixel.
- x = valeur de dimension.
- ß0 = interception avec l’axe des y.
- ß1 = pente linéaire ou taux de variation.
ß1 > 0 indique une tendance croissante.
ß1 < 0 indique une tendance décroissante.
- Polynomial (Polynomial) : la ligne de tendance polynomiale est une courbe utile pour les données qui fluctuent. Dans ce cas, une valeur d’ordre polynomial est utilisée pour indiquer le nombre maximum de fluctuations qui se produisent. La formule de la ligne de tendance polynomiale est la suivante :

- y = valeur variable du pixel
- x = valeur de dimension
- ß0, ß1, ß2, ß3, ..., ßn = coefficients constants
- Harmonic (Harmonique) : la ligne de tendance harmonique est la courbe périodique la plus adaptée pour décrire des données qui suivent un modèle cyclique, telles que des changements de température saisonniers. La formule de la ligne de tendance harmonique est la suivante :

- y = valeur variable du pixel
- t = date julienne
- ß0 = interception avec l'axe des y
- ß1 = taux de variation
- α, γ = coefficients des changements d’une année à l’autre ou au cours d’une même année
- ω = i
- f = fréquence harmonique
Vous avez un commentaire à formuler concernant cette rubrique ?