L’outil Redimensionner par fonction permet d’utiliser une fonction mathématique (ligne ou courbe) pour attribuer des valeurs d’adéquation à un raster en entrée sur une échelle continue (généralement de 1 à 10). Le redimensionnement est particulièrement utile dans la modélisation d’aptitude. Il arrive fréquemment que l’aptitude varie en fonction des valeurs du critère, et souvent de manière non linéaire. Par exemple, les emplacements de cellule à proximité de routes feront sans doute l’objet de la préférence la plus élevée dans un modèle d’adéquation de logement puisque le coût de raccordement de ces sites au réseau électrique est moindre. Plus la route est éloignée, plus le coût de raccordement électrique risque d’augmenter de façon exponentielle. Ainsi, l’adéquation des sites éloignés d’une route risque de diminuer considérablement. Une fois l’impact du coût déterminé, la diminution exponentielle de la préférence est traduite sur l’échelle d’adéquation continue spécifiée, comprise entre 1 et 10, par exemple. Pour identifier les sites les mieux adaptés à la construction de logements, le critère de coût mis à l’échelle peut alors être intégré à l’autre critère mis à l’échelle, à savoir une pente, un aspect et une distance par rapport aux écoles.
Quatre éléments doivent être pris en compte lors de l’application de cet outil :
- Comprendre et définir l’interaction des préférences entre le phénomène et le critère
- Sélectionner la fonction de transformation qui capture le mieux cette interaction des préférences (par exemple, augmentation exponentielle)
- Modifier éventuellement les paramètres de la fonction pour obtenir un meilleur ajustement
- Définir une échelle d’aptitude (évaluation) pour transformer les valeurs de préférence de la fonction (par exemple, 1 à 10)
L’outil Redimensionner par fonction développe vos options permettant de transformer des données en un modèle d’aptitude. Vous pouvez utiliser l’outil pour reclasser des données en catégories et l’outil Redimensionner par fonction pour redimensionner (reclasser) des données continues sans créer de catégories discrètes. L’outil Redimensionner par fonction propose diverses fonctions pour modéliser des degrés d’adéquation variables sur une échelle continue. Puisque l’outil redimensionne les valeurs du raster en entrée sur une échelle d’aptitude continue, les données ne sont pas agrégées en catégories. Cela vous permet de mieux capturer certaines interactions de préférences variables (dans l’exemple susmentionné, le coût varie en fonction de l’éloignement croissant de la route).
Les fonctions disponibles sont les suivantes : Exponentiel, Gaussienne, Grande, Linéaire, Logarithme, Désintégration logistique, Croissance logistique, MSLarge, MSSmall, Proche, Puissance, Petite et Linéaire symétrique. Voici des informations supplémentaires sur chaque fonction :
Vous pouvez définir des seuils supérieur et inférieur qui vous permettent de mieux contrôler le redimensionnement des valeurs en entrée. Pour plus d’informations, reportez-vous à la section Interaction des seuils inférieur et supérieur sur les valeurs en sortie.
Vocabulaire essentiel
Voici la définition de termes souvent utilisés pour expliquer l’outil Redimensionner par fonction.
- Phénomène - Elément modélisé (par exemple, un cerf, une maison, une route ou un centre commercial).
- Valeur de préférence - Valeur indiquant le degré de préférence du phénomène pour une entité à un emplacement spécifique.
- Critère - Entité qui correspond au phénomène (par exemple, pente, aspect, distance par rapport aux routes ou type d’utilisation du sol).
- Valeur d'aptitude - Identique à la valeur de préférence, à l'exception du fait que la préférence est établie dans le contexte d'un modèle d'aptitude.
- Echelle d’évaluation - Echelle relative sur laquelle placer les valeurs de préférence ou d’aptitude. En général, une cellule qui se voit attribuer une valeur d’évaluation supérieure contient des entités préférées par le phénomène par rapport au critère analysé. Les échelles d’évaluation les plus courantes sont les suivantes : 1 à 10, 0 à 1 et 1 à 100.
- Echelle d’aptitude - Identique à l’échelle d’évaluation.
- Valeurs continues - Valeurs d’un raster dont la signification est relative. Par exemple, une cellule d’une valeur de 100 mètres au-dessus du niveau de la mer présente une hauteur deux fois moins élevée qu’une cellule d’une valeur de 200 mètres. On peut compter comme exemples de données continues des valeurs d’altitude, de concentration d’ozone et d’aptitude.
- Valeurs catégorielles - Valeurs d’un raster dont la signification n’est pas relative. Par exemple, une cellule qui présente un type 4 d’utilisation du sol ne représente pas la moitié d’une cellule de type 8 en termes d’utilisation du sol. On peut citer comme exemples de données catégorielles le type d’utilisation du sol, le nom d’une région et le code postal.
- Echelle en sortie continue - Valeurs d’une plage spécifiée qui augmentent ou diminuent constamment sans classe discrète. Habituellement, les valeurs continues sont représentées par des valeurs à virgule flottante.
Transformation des données
L’outil Redimensionner par fonction permet de redimensionner des données continues sur une échelle d’adéquation spécifiée selon une fonction mathématique que vous sélectionnez, à savoir Exponentiel, Puissance et Logarithme. La transformation des données en entrée implique un processus à deux étapes. Tout d'abord, une fonction de transformation est appliquée, puis les valeurs de la fonction sont appariées à une échelle d'aptitude (habituellement comprise entre 1 et 10).
Application de la fonction de transformation
La fonction spécifiée est appliquée aux valeurs comprises entre les valeurs des seuils inférieur et supérieur.
Redimensionnement des données transformées sur l’échelle d’évaluation
Le diagramme suivant illustre l’appariement des valeurs de la fonction à l’échelle d’évaluation.
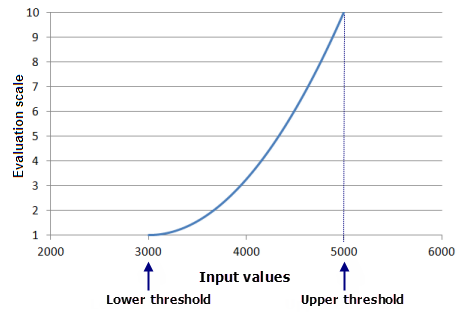
Les valeurs minimum et maximum transformées de la fonction, f(x), sont redimensionnées respectivement par rapport aux valeurs minimum et maximum de l’échelle d’évaluation. De nombreuses fonctions sont monotoniques (en augmentation ou diminution constantes). Ainsi, les seuils inférieur et supérieur seront habituellement appariés aux valeurs minimum et maximum de l'échelle d'évaluation, puisqu'il s'agit des valeurs f(x) les plus faibles et les plus élevées.
Dans l’exemple précédent, les seuils inférieur et supérieur correspondent aux valeurs minimum et maximum des données en entrée (3 000 et 5 000 respectivement). Ainsi, la valeur en entrée la plus faible se voit attribuer la valeur 1 sur une échelle d’évaluation comprise entre 1 et 10 ; la valeur en entrée la plus élevée correspond à 10, bien que ce ne soit pas nécessairement le cas. Si, par exemple, la fonction Puissance est appliquée à des données en entrée identiques (comprises entre 3 000 et 5 000) et si le seuil inférieur est défini sur 3 500 et le seuil supérieur sur 4 500, l’emplacement d’une cellule d’une valeur en entrée équivalente à 3 500 se verra attribuer la valeur 1 sur une échelle d’évaluation de la sortie comprise entre 1 et 10, et une valeur en entrée équivalente à 4 500 se verra attribuer la valeur 10. Toutes les autres valeurs seront comprises entre ces deux valeurs selon leur valeur transformée. Les valeurs en entrée inférieures au seuil inférieur et supérieures au seuil supérieur se voient attribuer les valeurs que vous spécifiez.
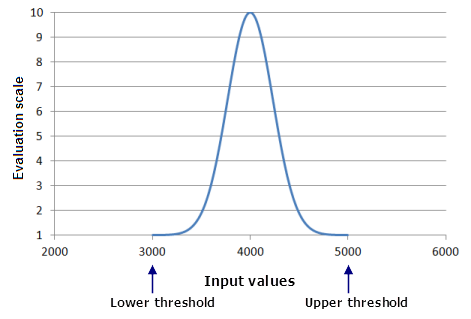
Toutes les fonctions ne sont pas en augmentation ou en diminution constante. Ainsi, les valeurs en entrée les plus faibles et les plus élevées ne sont pas toujours appariées aux valeurs d’évaluation les plus faibles et les plus élevées. Par défaut, avec la fonction Gaussienne, le centre est la valeur qui détermine le point le plus élevé de la fonction (valeur préférée). Il correspond au centre de vos données en entrée. Les emplacements qui présentent les valeurs en entrée minimum et maximum produiront les valeurs les plus faibles de la fonction, f(x), après l’application de la fonction Gaussienne. Ainsi, les cellules qui présentent les valeurs en entrée minimum et maximum se verront attribuer une valeur équivalente à 1 dans le raster en sortie. La valeur du centre produit la valeur la plus élevée de la fonction, f(x). Ainsi, les cellules contenant des valeurs en entrée correspondant à ce centre se verront attribuer une valeur égale à 10 sur le raster en sortie.
La fonction Gaussienne peut être utile dans un modèle d’adéquation permettant d’identifier l’habitat le mieux adapté à une espèce rare d’orchidée Masdevallia. L’orchidée est sensible à l’altitude. Elle pousse le mieux à une altitude d’environ 4 000 mètres. À une altitude supérieure, il fait trop froid pour l’orchidée et à une altitude inférieure, il fait trop chaud. Lorsque vous redimensionnez l'altitude, la valeur de 4 000 fait l'objet de la préférence la plus élevée et les autres valeurs d'altitude (supérieures et inférieures) font l'objet d'une préférence moindre.
Vous pouvez attribuer à une valeur en sortie une valeur en entrée inférieure au seuil inférieur ou supérieure au seuil supérieur (comprise ou non dans l’échelle d’évaluation, ou égale à NoData) en utilisant les paramètres Value below threshold (Valeur inférieure au seuil) et Value above threshold (Valeur supérieure au seuil). La fonction de transformation ne sera pas appliquée à ces emplacements.
Définition de la transformation
Deux approches principales permettent de définir une transformation continue :
- Acceptez les valeurs par défaut.
Les paramètres de contrôle de forme (voir la description ci-dessous) seront calculés pour ajuster la fonction entre les valeurs minimum et maximum du raster en entrée. Ce scénario dépend des données puisque la fonction est adaptée aux données.
- Sélectionnez la fonction qui permet de modéliser au mieux l’aptitude.
Modifiez les paramètres de contrôle de forme de la fonction pour ajuster sa forme afin qu’elle représente au mieux l’aptitude. Pour que la fonction ne dépende pas des données, attribuez aux seuils inférieur et supérieur les valeurs appropriées pour que la préférence du phénomène corresponde aux valeurs du critère, quelles que soient les valeurs des données en entrée.
Paramètres de la fonction de transformation
Types des paramètres de la fonction
Chaque fonction de transformation présente deux types de paramètres qui contrôlent les éléments suivants :
- Forme de la fonction
Parmi ces paramètres, citons les suivants : Base factor (Facteur de base), Input shift (Translation en entrée) et Midpoint (Centre). Ils définissent le degré d'augmentation ou de diminution de la fonction, le point de départ de l'évaluation de la fonction et les points de transition dans la fonction.
- Appariement de la fonction à l’échelle d’évaluation de l’aptitude
Parmi les paramètres de seuil, citons les suivants : Lower threshold (Seuil inférieur) et Value above threshold (Valeur supérieure au seuil).
Format des paramètres de fonctions
Voici le format habituel et les caractéristiques des paramètres de chaque fonction :
- Fonction ({Paramètre de forme 1}, {Paramètre de forme 2}, {Paramètre de forme 3}, {Seuil inférieur}, {Valeur inférieure au seuil}, {Seuil supérieur}, {Valeur supérieure au seuil})
Pour ces paramètres
- Chaque fonction comprend des paramètres de contrôle de forme et les paramètres de seuil respectifs.
- Le nombre de paramètres de contrôle de forme varie selon la fonction de transformation. Une fonction comprend habituellement deux paramètres, mais parfois trois.
- Les paramètres de seuil sont cohérents sur l’ensemble des fonctions.
- Les valeurs par défaut des paramètres de contrôle de forme sont calculées à l’aide des valeurs des données du raster en entrée.
- Tous les paramètres de la fonction sont facultatifs.
- Les valeurs des paramètres Lower threshold (Seuil inférieur) et Value above threshold (Valeur supérieure au seuil) peuvent être un nombre (double) ou la chaîne "NoData". Tous les autres paramètres sont de type double.
Exemple de format de la fonction Exponentiel
Pour illustrer l’application du format susmentionné à une fonction de transformation spécifique, voici les paramètres qui sont utilisés avec une fonction de transformation (Transformation function) de type Exponentiel :
Exponential (Exponentiel) (Input shift [Translation en entrée], Base factor [Facteur de base], Lower threshold [Seuil inférieur], Value below threshold [Valeur inférieure au seuil], Lower threshold, Value above threshold [Valeur supérieure au seuil])
Les paramètres Translation en entrée et Facteur de base permettent de contrôler la forme. Seuil inférieur, Valeur inférieure au seuil, Seuil supérieur et Valeur supérieure au seuil sont des paramètres de seuil.
Par défaut, les valeurs de données minimum et maximum définissent les limites inférieure et supérieure de la fonction.
Interaction des paramètres dans la boîte de dialogue des outils
Pour le paramètre Raster en entrée, la valeur du Seuil inférieur est définie sur la valeur minimum de ce raster, la valeur du Seuil supérieur est définie sur la valeur maximum du raster et les paramètres de contrôle de forme (par exemple Translation en entrée, Facteur de base et Centre) sont calculés automatiquement pour ajuster (contraindre) au mieux la fonction entre les valeurs des paramètres Seuil inférieur et Seuil supérieur.
Il existe une interaction entre les paramètres de seuils qui contrôlent l’appariement des valeurs de la fonction à l’échelle d’adéquation avec les paramètres de contrôle de forme qui définissent la courbe de la fonction. Par exemple, une fois les valeurs par défaut déterminées, vous pouvez attribuer une valeur supérieure au paramètre Seuil supérieur. Les paramètres de contrôle de forme associés seront recalculés et mis à jour dans la boîte de dialogue (par exemple Translation en entrée et Facteur de base). Toutefois, si vous attribuez une nouvelle valeur à un des paramètres de contrôle de forme (par exemple, un nouveau facteur de base [Base factor]), la relation avec les paramètres de seuil associés déterminant l’appariement à l’échelle d’adéquation est rompue et c’est vous qui contrôlez alors l’opération. Avec la fonction Exponentiel, par exemple, si vous indiquez un nouveau facteur de base [Base factor] et que vous modifiez le seuil supérieur (Upper threshold), un nouveau facteur de base [Base factor] n’est pas automatiquement recalculé. L’outil utilisera le Facteur de base que vous avez spécifié. Dans un autre exemple illustrant la fonction Linéaire, le paramètre Seuil supérieur a, par défaut, la valeur maximum du Raster en entrée. Si vous indiquez une valeur supérieure pour le Seuil supérieur, le paramètre Maximum sera automatiquement mis à jour pour cette fonction Linéaire. Toutefois, si vous indiquez une nouvelle valeur Maximum et que vous modifiez la valeur du Seuil supérieur, la valeur Maximum n’est pas modifiée.
Grâce à cette interaction dans la boîte de dialogue, la fonction est ajustée par défaut entre les valeurs de Seuil inférieur et de Seuil supérieur définies à l’origine sur les valeurs minimum et maximum du Raster en entrée. Toutefois, vous pouvez contrôler intégralement la forme de la fonction et l’appariement à l’échelle d’évaluation en indiquant les valeurs de votre choix.
Si vous modifiez le paramètre d’une fonction et souhaitez rétablir sa valeur par défaut, sélectionnez et supprimez la valeur du paramètre, puis cliquez dans le champ d’un autre paramètre pour que la valeur vide soit recalculée et que la valeur par défaut soit rétablie. Par exemple, si vous avez spécifié une valeur pour le paramètre Base factor (Facteur de base), mais que vous souhaitez que la fonction soit de nouveau ajustée entre les valeurs des paramètres Lower threshold (Seuil inférieur) et Upper threshold (Seuil supérieur), supprimez la valeur du paramètre Base factor (Facteur de base), cliquez dans le champ d’un autre paramètre afin de calculer pour le paramètre Base factor (Facteur de base) une nouvelle valeur qui ajuste la fonction entre les seuils.
Remarque :
Les fonctions MSSmall et MSLarge n’adoptent pas ce comportement d’interaction, car elles dépendent de la moyenne et de l’écart type du jeu de données en entrée.
Vous avez un commentaire à formuler concernant cette rubrique ?