L’outil Ombrage permet d’obtenir l’éclairage hypothétique d’une surface en déterminant les valeurs d’éclairage de chaque cellule d’un raster. Cette fonction définit la position d’une source lumineuse hypothétique et calcule les valeurs d’éclairage de chaque cellule par rapport aux cellules voisines. L'ombrage améliore nettement la visualisation d'une surface lors de l'affichage d'analyses ou de diagrammes, en particulier si vous avez recours à la transparence.
Par défaut, l'ombre et la lumière sont des nuances de gris associées à des entiers de 0 à 255 (du noir au blanc).
Paramètres d'ombrage
Lors de la création d'une carte d'ombrage pour un emplacement donné, le facteur principal est la position du soleil dans le ciel.
Azimut
L'azimut correspond à la direction angulaire du soleil, mesurée à partir du nord, dans le sens horaire, par degrés, de 0 à 360. Un azimut de 90 degrés correspond à l’est. L'azimut par défaut est 315 degrés (NO).

Altitude
L'altitude représente la pente ou l'angle de la source d'éclairage au-dessus de la ligne d'horizon. Les unités sont les degrés, de 0 (à l'horizon) à 90 (à la verticale). La valeur par défaut est de 45 degrés.
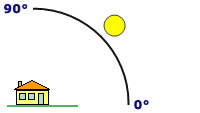
Exemple d’ombrage
L’exemple d’ombrage suivant a un azimut de 315 degrés et une altitude de 45 degrés.

Utilisation de l'ombrage dans l'affichage
En plaçant un raster d’altitude sur un raster d’ombrage et en ajustant la transparence du raster d’altitude, vous pouvez créer une carte en relief visuellement attrayante d’un paysage. Pour savoir comment ajuster l’affichage et l’apparence, reportez-vous à la rubrique Apparence des images.

Vous pouvez ajouter d'autres couches, telles que des types d'utilisation du sol, de la végétation, des routes ou des cours d'eau pour enrichir les informations présentées.
Utilisation de l'ombrage dans une analyse
En modélisant l'ombrage (l'option par défaut), vous pouvez calculer l'éclairage local et déterminer si la cellule est ou non dans l'ombre.
En modélisant les ombres, vous pouvez identifier chaque cellule qui se trouve à l’ombre d’une autre cellule à un moment donné de la journée. Les cellules situées dans l’ombre d’une autre cellule sont codées sur 0 ; toutes les autres cellules sont codées sur des entiers compris entre 1 et 255. Vous pouvez reclasser toutes les valeurs supérieures à 1 sur 1 et générer ainsi un raster en sortie binaire. Dans l’exemple ci-dessous, les zones noires sont à l’ombre. L'azimut est le même dans chaque image, mais l'angle du soleil (altitude) a été modifié.

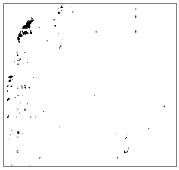
Calcul de l'ombrage
Pour calculer la valeur d’ombrage, l’altitude et l’azimut de la source d’éclairage sont d’abord requis. Ces valeurs seront traitées avec les calculs de pente et d'exposition, afin de déterminer la valeur d'ombrage finale de chaque cellule du raster en sortie.
Algorithme d'ombrage
L'algorithme de calcul de la valeur d'ombrage est le suivant :
(1) Ombrage = 255.0 * ((cos(Zenith_rad) * cos(Slope_rad)) + (sin(Zenith_rad) * sin(Slope_rad) * cos(Azimuth_rad - Aspect_rad)))Notez que si le calcul de la valeur d'ombrage est inférieur à 0, la valeur de cellule en sortie est égale à 0.
Calculer l'angle d'éclairage
L’altitude de la source d’éclairage est spécifiée en degrés au-dessus de l’horizontale. Toutefois, la formule de calcul de la valeur d’ombrage nécessite que l’angle soit représenté en radians et en déflexion de la verticale. On appelle zénith la direction tout droit vers le haut à partir de la surface (directement au-dessus). L’angle zénithal se mesure du point zénithal en direction de la source d’éclairage. Il est le complément à 90 degrés de l’altitude. Pour calculer l’angle d’éclairage, commencez par convertir l’angle d’altitude en angle zénithal. Convertissez ensuite l'angle en radians.
Conversion de l'angle d'altitude en angle zénithal :
(2) Zenith_deg = 90.0 - AltitudeConversion en radians :
(3) Zenith_rad = Zenith_deg * pi / 180.0Calculer la direction de l'éclairage
La direction de la source d’éclairage, azimut, est spécifiée en degrés. La formule d’ombrage nécessite que cet angle soit en unités de radians. Commencez par convertir l’angle azimutal de son unité géographique (cap de boussole) en une unité mathématique (angle droit). Convertissez ensuite l'angle azimutal en radians.
Modification de la mesure de l'angle azimutal :
(4) Azimuth_math = 360.0 - Azimuth + 90.0Notez que si Azimuth_math >= 360,0, alors :
(5) Azimuth_math = Azimuth_math - 360.0Conversion en radians :
(6) Azimuth_rad = Azimuth_math * pi / 180.0Calculer la pente et l'exposition
Une fenêtre mobile 3 x 3 se déplace dans chaque cellule du raster en entrée. Pour chaque cellule située au centre de la fenêtre, une valeur d'exposition et de pente est calculée à l'aide d'un algorithme qui intègre les valeurs des huit voisins de la cellule. Les cellules sont identifiées par les lettres a à i ; e représentant la cellule pour laquelle l'aspect est calculé.
Le taux de variation dans la direction x pour la cellule e est calculé avec l'algorithme suivant :
(7) [dz/dx] = ((c + 2f + i) - (a + 2d + g)) / (8 * taille de cellule)Le taux de variation dans la direction y pour la cellule e est calculé avec l'algorithme suivant :
(8) [dz/dy] = ((g + 2h + i) - (a + 2b + c)) / (8 * taille de cellule)La descente la plus raide depuis chaque cellule de la surface est la pente. L'algorithme de calcul de la pente en radians, incorporant le facteur z, est le suivant :
(9) Slope_rad = ATAN (z_factor * √ ([dz/dx]2 + [dz/dy]2))La direction dans le sens de la pente descendante la plus raide est l’exposition. L’exposition en radians est définie dans la plage de 0 à 2 pi, avec 0 vers l’est. L'exposition est déterminée selon les règles de l'algorithme suivant :
(10) If [dz/dx] is non-zero: Aspect_rad = atan2 ([dz/dy], -[dz/dx]) if Aspect_rad < 0 then Aspect_rad = 2 * pi + Aspect_rad If [dz/dx] is zero: if [dz/dy] > 0 then Aspect_rad = pi / 2 else if [dz/dy] < 0 then Aspect_rad = 2 * pi - pi / 2 else Aspect_rad = Aspect_radExemple de calcul de l'ombrage
Dans cet exemple, la valeur d'ombrage de la cellule centrale de la fenêtre mobile est calculée.
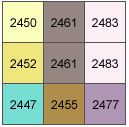
La taille de cellule est 5 unités. Une altitude par défaut de 45 degrés et un azimut de 315 degrés seront utilisés.
- Angle d'éclairage
Le calcul de l'angle zénithal à partir de l'équation 2 est le suivant :
(2) Zenith_deg = 90.0 - Altitude = 90.0 - 45.0 = 45.0Et, converti en radians à partir de l'équation 3, cela donne :
(3) Zenith_rad = Zenith_deg * pi / 180.0 = 45.0 * 3.1415926536 / 180.0 = 0.7853981634 - Direction de l'éclairage
Le calcul permettant de convertir l'angle azimutal, d'un angle géographique en angle mathématique, via l'équation 4, est le suivant :
(4) Azimuth_math = 360.0 - Azimuth + 90.0 = 360.0 - 315.0 + 90.0 = 135.0La conversion de l'angle azimutal en radians avec l'équation 6 est la suivante :
(6) Azimuth_rad = Azimuth_math * pi / 180.0 = 135.0 * 3.1415926536 / 180 = 2.3561944902
- Pente et exposition
Le calcul du taux de variation dans la direction x pour la cellule centrale e est le suivant :
(7) [dz/dx] = ((c + 2f + i) - (a + 2d + g)) / (8 * taille de cellule) = ((2483 + 4966 + 2477) - (2450 + 4904 + 2447)) / (8 * 5) = (9926 - 9801) / 40 = 3.125Le calcul du taux de variation dans la direction y pour la cellule centrale e est le suivant :
(8) [dz/dy] = ((g + 2h + i) - (a + 2b + c)) / (8 * taille de cellule) = (2447 + 4910 + 2477) - (2450 + 4922 + 2483) / (8 * 5) = (9834 - 9855) / 40 = -0.525Le calcul de l'angle de pente est le suivant :
(9) Slope_rad = ATAN ( z_factor * √ ([dz/dx]2 + [dz/dy]2)) = atan(1 * sqrt((3.125 * 3.125) + (-0.525 * -0.525))) = atan(1 * sqrt(10.04125 + 0.275625)) = atan(1 * 3.1687931457) = 1.2651101670Le calcul de l’angle Aspect_rad depuis la règle 10 est le suivant (car dz/dx n’est pas nul dans cet exemple) :
Aspect_rad = atan2 ([dz/dy], -[dz/dx]) = atan2(-0.525, -3.125) = -2.9751469600Puisque cette valeur est inférieure à 0, cette partie de la règle s'applique :
Aspect_rad = 2 * pi + Aspect_rad = 2 * 3.1415926536 + -2.9751469600 = 3.3080383471 - Ombrage
Le dernier calcul de l'ombrage est le suivant :
Ombrage = 255.0 * ((cos(Zenith_rad) * cos(Slope_rad)) + (sin(Zenith_rad) * sin(Slope_rad) * cos(Azimuth_rad - Aspect_rad))) = 255.0 * ((cos(0.7857142857) * cos(1.26511)) + (sin(0.7857142857) * sin(1.26511) * cos(2.3571428571 - 3.310567))) = 153.82
Puisque le raster en sortie est de type entier, la valeur d’ombrage de la cellule centrale e = 154.
Bibliographie
Burrough, P. A., and R. A. McDonell. 1998. Principles of Geographical Information Systems. New York: Oxford University Press.
Vous avez un commentaire à formuler concernant cette rubrique ?