El análisis de regresión se utiliza para comprender, modelar, predecir y explicar fenómenos complejos. Ayuda a responder preguntas como "¿Por qué hay lugares de Estados Unidos donde las notas de examen suelen estar por encima de la media nacional?" o "¿Por qué hay áreas de la ciudad con tasas tan altas de robos en zonas residenciales?". Puede utilizar el análisis de regresión para explicar la obesidad infantil, por ejemplo, mediante un conjunto de variables relacionadas como los ingresos, la educación y la accesibilidad a alimentos sanos.
Por lo general, el análisis de regresión le ayuda a responder a estas preguntas de por qué, para que pueda hacer algo al respecto. Si, por ejemplo, comprueba que la obesidad infantil es menor en las escuelas que sirven frutas y vegetales frescos a la hora de comer, puede utilizar esa información para orientar la política y tomar decisiones sobre los programas de almuerzo escolar. Del mismo modo, conocer las variables que ayudan a explicar las tasas altas de delincuencia puede permitirle hacer predicciones sobre la futura delincuencia de manera que los recursos de prevención puedan asignarse de forma más efectiva.
Estas son las cosas que sí le dicen sobre el análisis de regresión.
Lo que no le dicen sobre el análisis de regresión es que no siempre resulta fácil encontrar un conjunto de variables explicativas que le permitan responder a su pregunta o explicar el fenómeno complejo que intenta modelar. La obesidad infantil, el crimen, los resultados de las pruebas y casi todas las cosas que quizá desee modelar mediante el análisis de regresión son cuestiones complicadas que rara vez tienen respuestas sencillas. Es posible que, si alguna vez ha intentado construir su propio modelo de regresión, esto no es nada nuevo para usted.
Afortunadamente, al ejecutar la herramienta Regresión lineal generalizada (GLR), se le ofrece un conjunto de diagnósticos que le pueden ayudar para determinar si tiene un modelo especificado adecuadamente, es decir, uno en el que pueda confiar. Este documento examina y explica varias de estas comprobaciones que querrá realizar para poder confiar en su modelo. Estos diagnósticos, así como las técnicas que utiliza para resolver algunos de los problemas de análisis de regresión más habituales, son recursos que le facilitarán el trabajo.
Sugerencia:
Una vez comprenda la información que se le presenta a continuación, puede que decida utilizar la herramienta Regresión exploratoria para ayudarle a encontrar un modelo que satisfaga todos los requisitos del método GLR.
Introducción
Elegir la variable que desee entender, predecir o modelar es su primera tarea. Esta variable se conoce como la variable dependiente. La obesidad infantil, el crimen y las puntuaciones de los exámenes serían variables dependientes que se están modelando en los ejemplos descritos anteriormente.
A continuación, tendrá que determinar qué factores podrían ayudar a explicar su variable dependiente. Estas variables se conocen como las variables explicativas. En el ejemplo de obesidad infantil, las variables explicativas podrían ser cosas como los ingresos, la educación y la accesibilidad a alimentos sanos. Deberá hacer su investigación aquí para identificar todas las variables explicativas que podrían ser importantes; consulte la teoría y literatura existente, hable con los expertos y confíe siempre en su sentido común. El estudio preliminar que realiza directamente aumentará la posibilidad de encontrar un buen modelo.
Con la variable dependiente y las variables explicativas de candidato seleccionadas, está listo para ejecutar el análisis. Se recomienda que comience su análisis de regresión con Regresión lineal generalizada (GLR) o Regresión exploratoria, ya que estas herramientas realizan pruebas de diagnóstico importantes que indican si ha dado con un modelo útil o si todavía tiene trabajo por delante.
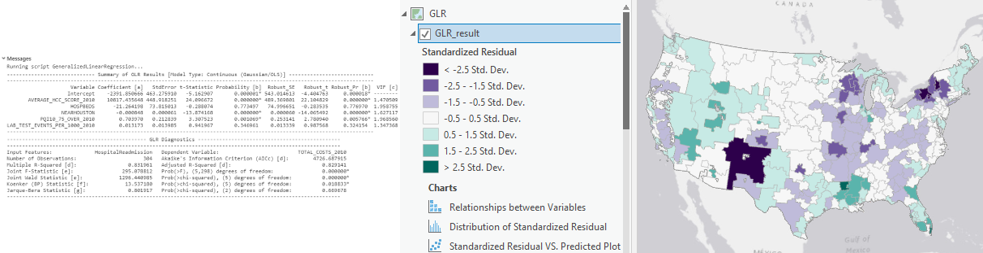
La herramienta GLR genera varias salidas, incluido un mapa de los residuales de regresión, gráficos y un informe de resumen. El mapa de residuales de regresión muestra las predicciones escasas y excesivas de su modelo, y analizar este mapa es un paso importante en la búsqueda de un buen modelo. El informe de resumen es en gran medida numérico e incluye todos los diagnósticos que utilizará al revisar los seis controles a continuación.
Seis comprobaciones de diagnóstico
Comprobación 1: ¿Estas variables explicativas están ayudando a mi modelo?
Después de consultar la teoría y la investigación existentes, habrá identificado un conjunto de variables explicativas de candidatos. Tendrá buenas razones para incluir cada uno en su modelo. Sin embargo, después de ejecutar el modelo, encontrará que algunas de sus variables explicativas son estadísticamente significativas y otras no.
¿Cómo sabrá qué variables explicativas son importantes? La herramienta GLR calcula un coeficiente para cada variable explicativa en el modelo y realiza una prueba estadística para determinar si esa variable es una ayuda o no para el modelo. La prueba estadística calcula la probabilidad de que el coeficiente sea realmente de cero. Si el coeficiente es cero (o muy cerca de cero), la variable explicativa asociada no ayuda al modelo. Cuando la prueba estadística devuelve una probabilidad pequeña (valor P) para una variable explicativa determinada, sin embargo, indica que es poco probable (la probabilidad es muy pequeña) que el coeficiente es cero. Si la probabilidad es menor que 0,05, un asterisco situado junto a la probabilidad del informe de resumen de GLR indica que la variable explicativa asociada es importante para el modelo (es decir, su coeficiente es estadísticamente significativo en un nivel de confianza del 95 por ciento). Así que está buscando las variables explicativas asociadas con las probabilidades estadísticamente significativas (busque las que tienen asteriscos).
La herramienta GLR calcula tanto la probabilidad como la probabilidad robusta de cada variable explicativa. Con datos espaciales, no es raro que las relaciones que está modelando varíen en toda el área de estudio. Estas relaciones se caracterizan como no estacionarias. Cuando las relaciones no son estacionarias, solo puede confiar en las probabilidades sólidas para decirle si una variable explicativa es estadísticamente significativa.
Cómo sabrá si las relaciones del modelo no son estacionarias? Otra prueba estadística incluida en el informe de resumen de GLR es la estadística de Koenker (estadística de Breusch-Pagan estudentizada de Koenker) para la ausencia de estacionariedad. Un asterisco junto al valor p de Koenker indica que las relaciones que está modelando exhiben una no estacionariedad estadísticamente significativa, por lo tanto, asegúrese de consultar las probabilidades sólidas.
Normalmente, eliminará las variables explicativas de su modelo si no son estadísticamente significativas. Sin embargo, si la teoría indica que una variable es muy importante, o si una variable específica es el enfoque de su análisis, puede conservarla incluso si no es estadísticamente significativa.
Nota:
Durante el proceso de buscar un modelo GLR especificado adecuadamente, es probable que pruebe diversas variables explicativas. Tenga en cuenta que los coeficientes de la variable explicativa (y su significancia estadística) pueden cambiar radicalmente dependiendo de la combinación de las variables que incluye en el modelo.
Comprobación 2: ¿Las relaciones son lo que esperaba?
No solo es importante determinar si una variable explicativa está realmente ayudando a su modelo, sino que también querrá verificar el signo (+/-) asociado con cada coeficiente para asegurarse de que la relación es lo que esperaba. El signo del coeficiente de la variable explicativa indica si la relación es positiva o negativa. Supongamos que modela la delincuencia, por ejemplo, y una de las variables explicativas es el ingreso promedio de la vecindad. Si el coeficiente de los ingresos variable es un número negativo, significa que los crímenes tienden a disminuir a medida que aumentan los ingresos de la vecindad (una relación negativa). Si modela la obesidad infantil y la accesibilidad a la comida rápida variable tuviera un coeficiente positivo, indicaría que la obesidad infantil tiende a aumentar a medida que aumenta el acceso a la comida rápida (una relación positiva).
Cuando crea la lista de variables explicativas de candidatos, debe incluir para cada variable la relación (positivo o negativo) que espera. Le resultará difícil confiar en un modelo que informa sobre relaciones que no coindicen con teorías ni se adaptan al sentido común. Supongamos que está construyendo un modelo para predecir las frecuencias de incendios forestales y el modelo de regresión devolvió un coeficiente positivo para la variable de precipitación. Es probable que no espere que los incendios forestales aumenten en ubicaciones donde llueve mucho.
A menudo, los signos de coeficiente inesperados indican otros problemas del modelo que surgirán a medida que sigue trabajando con las otras comprobaciones de diagnóstico. Solo puede confiar en la señal y la fuerza de los coeficientes de variable explicativa si el modelo pasa todos estos. Si encuentra un modelo que pasa todos los controles a pesar del inesperado signo del coeficiente, puede haber descubierto una oportunidad para aprender algo nuevo. Quizás existe una relación positiva entre la frecuencia de incendios forestales y las precipitaciones porque la principal fuente de incendios forestales en su área de estudio es un rayo. Puede ser que valga la pena intentar obtener datos sobre rayos para su área de estudio para ver si mejora el rendimiento del modelo.
Comprobación 3: ¿Algunas de las variables explicativas son redundantes?
Al elegir variables explicativas para incluirlas en su análisis, busque variables que exploren distintos aspectos de lo que intenta modelar; evite las variables que ofrecen información similar. Por ejemplo, si está tratando de modelar los valores de viviendas, probablemente no incluiría variables explicativas tanto para la superficie en pies cuadrados de la vivienda y el número de dormitorio. Ambas variables se refieren al tamaño de la casa, e incluir ambos podría hacer que su modelo fuera inestable. Por último, no puede confiar en un modelo que incluye variables redundantes.
¿Cómo sabrá si dos o más variables son redundantes? Afortunadamente, siempre que tenga más de dos variables explicativas, la herramienta GLR calcula un factor de inflación de la varianza (VIF) para cada variable. El valor VIF es una medida de redundancia de la variable y puede ayudarle a decidir qué variables se pueden quitar de su modelo sin poner en peligro el poder explicativo. Como regla general, un valor VIF mayor que 7,5 es problemático. Si tiene dos o más variables con valores VIF arriba de 7,5, debe quitarlos uno a la vez y volver a ejecutar OLS hasta que la redundancia desaparezca. Tenga en cuenta que no desea quitar todas las variables con valores VIF altos. En el ejemplo de modelar los valores de las viviendas, la superficie en pies cuadrados y el número de dormitorios probablemente tendrá los valores VIF inflados. Sin embargo, tan pronto elimina una de esas dos variables, se elimina la redundancia. Es importante incluir una variable que refleje el tamaño de la casa; simplemente no desea modelar este aspecto de los valores de las viviendas de manera redundante.
Comprobación 4: ¿Mi modelo está sesgado?
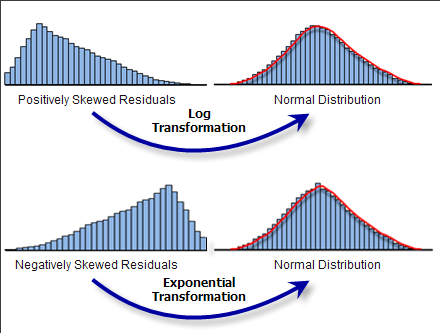
Puede parecer una pregunta complicada, pero la respuesta es muy sencilla. Una vez que tenga un modelo GLR especificado adecuadamente, los residuales del modelo (las sobrepredicciones y las subpredicciones) se suelen distribuir con un valor medio de cero (como en una curva de campana). No obstante, si el modelo está sesgado, la distribución de los residuales no está equilibrada, como se muestra a continuación. No se puede confiar totalmente en los resultados anticipados cuando el modelo está sesgado. Existen varias estrategias para ayudarle a corregir este problema.
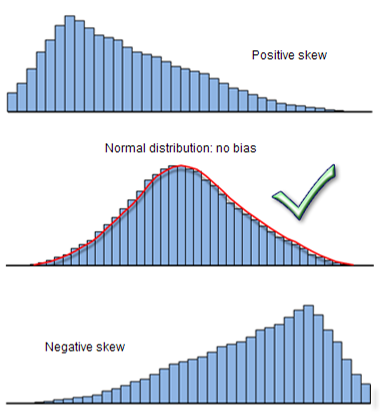
Un diagnóstico de Jarque-Bera importante estadísticamente (busque el asterisco) indica que su modelo está sesgado. A veces el modelo está haciendo un buen trabajo para los valores bajos pero no está anticipando bien para los valores altos (o viceversa). Con el ejemplo de la obesidad infantil, significaría que el modelo funciona bien en las ubicaciones con poca obesidad infantil, pero si esta es elevada, las predicciones no funcionan. El sesgo del modelo también puede ser el resultado de los valores atípicos que están influyendo en la estimación del modelo.
Para ayudar a solucionar el sesgo del modelo, cree una matriz de gráficos de dispersión para todas las variables de su modelo. Una relación no lineal entre la variable dependiente y una de las variables explicativas es una causa común de la influencia del modelo. Estas relaciones pueden tener el aspecto de una línea curvada en la matriz de gráficos de dispersión. Las relaciones lineales parecen líneas diagonales.
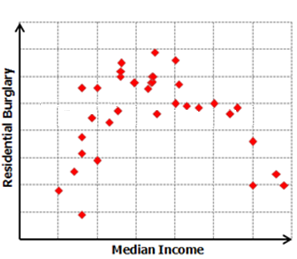
Si observa que la variable dependiente mantiene una relación no lineal con una de las variables explicativas, tendrá que hacer algunos ajustes. GLR es un método de regresión lineal que asume que las relaciones que está modelando son lineales. Cuando no lo son, puede intentar transformar sus variables para ver si esto crea relaciones que son más lineales. Las transformaciones comunes incluyen el registro y el exponencial. Si algunas de sus variables explicativas son muy sesgadas, es posible que pueda quitar de la influencia del modelo al transformarlos también.
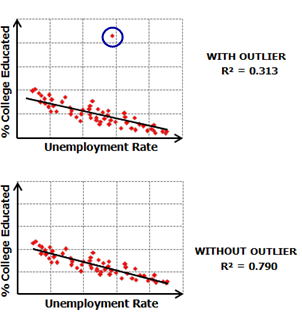
Una matriz de gráficos de dispersión también revelará valores atípicos de los datos. Para ver si un valor atípico influye en su modelo, intente ejecutar Regresión lineal generalizada (GLR) con y sin un valor atípico y compruebe cuánto cambia el rendimiento del modelo y si al quitarlo se corrige el sesgo del modelo. En algunos casos (especialmente si piensa que los valores atípicos representan datos erróneos), es posible que pueda sacar los valores atípicos de su análisis.
Comprobación 5: ¿He encontrado todas las variables explicativas clave?
A menudo, usted inicia un análisis con hipótesis sobre las variables que van a ser indicadores importantes. Quizá usted considera que 5 variables particulares producirán un buen modelo, o quizás tiene una lista de firmas de 10 variables que cree pueden estar relacionadas. Si bien es importante abordar el análisis de regresión con una hipótesis, también es importante dejar que su creatividad y conocimientos le ayuden a seguir investigando. Resista la tentación de limitarse a su primera lista de variables, e intente considerar todas las posibles variables que puedan afectar lo que está modelando. Cree mapas temáticos de cada una de las variables explicativas del candidato y compárelas a un mapa de la variable dependiente. Revise la literatura pertinente. Utilice su intuición para buscar relaciones en sus datos representados cartográficamente. Intente concebir tantas variables espaciales candidatas como sea posible, como la distancia desde el centro urbano, la proximidad a carreteras principales o el acceso a grandes masas de agua. Estos tipos de variables serán especialmente importantes para los análisis cuando considere que los procesos geográficos afectan las relaciones en los datos. Hasta que encuentre variables explicativas que capturen efectivamente la estructura espacial en su variable dependiente, de hecho, a su modelo le faltarán variables explicativas clave y no podrá pasar todas las verificaciones de diagnóstico que aquí se describen.
La evidencia de que le falta una o más variables explicativas clave es la autocorrelación espacial estadísticamente significativa de los residuales del modelo. En el análisis de regresión, los problemas con residuales autocorrelacionados espacialmente suelen adoptar la forma de clustering: las sobrepredicciones se agrupan entre ellas, al igual que las subpredicciones. ¿Cómo sabrá si tiene una autocorrelación espacial estadísticamente significativa en los residuales del modelo? Al ejecutar la herramienta Autocorrelación espacial en los residuales de regresión, sabrá si tiene un problema de autocorrelación espacial. Una puntuación z estadísticamente significativa indica que le faltan variables explicativas clave al modelo.
Encontrar esas variables explicativas faltantes a menudo es tanto un arte como una ciencia. Pruebe estas estrategias para ver si resultan útiles:
Examinar el mapa residual de GLR
La salida estándar de la herramienta Regresión lineal generalizada (GLR) es un mapa de los residuales del modelo. Las áreas en morado oscuro indican que los valores reales (la variable dependiente) son mayores que lo que predijo el modelo. Las áreas en turquesa más oscuro muestran dónde son los valores reales menores que los predichos. En ocasiones, con solo ver el mapa residual se hará una idea de lo que se podría estar perdiendo. Si observa que está haciendo predicciones excesivas de forma consistente en áreas urbanizadas, por ejemplo, es posible que quiera considerar agregar una variable que refleje la distancia a los centros urbanos. Si parece ser que las predicciones excesivas están asociadas con los picos de montaña o fondos de los valles, quizás necesite una elevación variable. ¿Ve clusters regionales, o puede reconocer las tendencias en los datos? Si es así, puede que resulte eficaz crear una variable falsa para captar estas diferencias regionales. El ejemplo clásico de una variable de simulación es aquel que distingue las entidades urbanas y rurales. Al asignar un valor de 1 a todas las entidades rurales y un valor de 0 al resto de entidades, puede capturar relaciones espaciales del paisaje que podrían ser importantes para su modelo. A veces la creación de un mapa de punto caliente de los residuales de modelo le ayudará a visualizar patrones regionales amplios.
Descubrir las variables espaciales faltantes no solo tiene el potencial de mejorar el modelo, sino que este proceso también puede ayudarle a comprender mejor el fenómeno que está modelando en nuevas e innovadoras maneras.
Nota:
Aunque resulta útil incluir las variables falsas del régimen espacial en su modelo GLR, plantéese eliminarlas cuando ejecute Regresión ponderada geográficamente (GWR) para evitar problemas con la multicolinealidad local.
Examinar la no estacionariedad
También puede probar a ejecutar la Regresión ponderada geográficamente y crear superficies de coeficiente para cada variable explicativa o mapa de los valores R2 locales. Seleccione el modelo GLR que funciona bien (uno con un valor R2 ajustado elevado que supere todas o la mayoría de las comprobaciones de diagnóstico). Dado que GWR crea una ecuación de regresión para cada entidad de su área de estudio, las superficies de coeficiente ilustran cómo fluctúan geográficamente las relaciones entre la variable dependiente y cada variable explicativa; el mapa de valores R2 locales muestra variaciones en la potencia explicativa del modelo. En ocasiones, al ver estas variaciones geográficas, surgen ideas sobre qué variables pueden faltar: una caída en la potencia explicativa cerca de autopistas importantes, un descenso en la distancia desde la costa, un cambio en el signo de los coeficientes cerca de una región industrial, o un límite o tendencia fuerte de este a oeste. Todo ello sería información sobre variables espaciales que podrían mejorar el modelo.
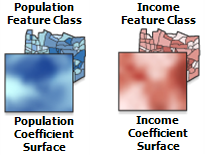
Al examinar las superficies de coeficiente, busque variables explicativas con coeficientes que cambien su signo de positivo a negativo. Es importante porque es probable que la GLR descuente el potencial predictivo de estas variables altamente no estacionarias. Considere, por ejemplo, la relación entre la obesidad infantil y el acceso a opciones de alimentos saludables. Puede ser que, en áreas de ingresos bajos con menos acceso a coches, estar lejos de un supermercado sea una barrera real para optar por alimentos saludables. Sin embargo, en áreas de ingresos altos con mayor acceso a vehículos, tener un supermercado a una corta distancia a pie puede que no sea conveniente; puede que la distancia hasta el supermercado no sea en absoluto una barrera para comprar alimentos saludables. Si bien la GWR puede modelar estos tipos de relaciones complejas, la GLR no puede. La GLR es un modelo global que espera que las relaciones de las variables sean uniformes (estacionarias) en toda el área de estudio. Cuando los coeficientes cambian de signo, se anulan entre sí. Piense en ello como (+1) + (-1) = 0. Si encuentra variables en las que los coeficientes cambian dramáticamente, en especial si cambian de signo, debería mantenerlas en su modelo, incluso si no son importantes estadísticamente. Estos tipos de variables serán efectivos cuando se traslada a GWR.
Intente adaptar la GLR a áreas de estudio de subconjuntos más pequeños.
GWR resulta muy útil al lidiar con la ausencia de estacionariedad, y puede ser tentador ir directamente a GWR sin buscar primero un modelo GLR especificado adecuadamente. Lamentablemente, la GWR no cuenta con todos los diagnósticos para ayudarle a descubrir si las variables explicativas son estadísticamente significativas, si los residuales se distribuyen con normalidad o, en última instancia, si dispone de un buen modelo. GWR no solucionará ningún modelo incorrectamente especificado, salvo que usted sepa con certeza que el único motivo por el que falla su modelo GLR en las seis comprobaciones es el resultado directo de la ausencia de estacionariedad. La evidencia de la no estacionariedad sería buscar variables explicativas que tengan una fuerte relación positiva en algunas partes del área de estudio y una fuerte relación negativa en otras partes. A veces, el problema no es con las variables explicativas individuales sino con el conjunto de variables explicativas que se utiliza en el modelo. Puede ser que un conjunto de variables ofrezca un buen modelo para una parte del área de estudio, pero otro conjunto de variables distintas funciona mejor en otro lugar. Para saber si ocurre aquí, puede seleccionar varias áreas de estudio de subconjuntos más pequeños e intentar adaptar modelos GLR a cada una. Seleccione las áreas del subconjunto basado en los procesos que considere que pueden estar relacionados con el modelo (áreas de altos ingresos versus áreas de bajos ingresos, viviendas nuevas versus viejas). Como alternativa, seleccione las áreas en función del mapa GWR de valores R2 locales; las ubicaciones con un bajo rendimiento del modelo se pueden modelar mejor con otro conjunto diferente de variables explicativas.
Sugerencia:
La herramienta Clustering multivariante restringido espacialmente puede ser de gran utilidad a la hora de identificar subregiones en un área de estudio más amplia.
Si encuentra modelos GLR especificados adecuadamente en varias áreas de estudio pequeñas, puede llegar a la conclusión de que la responsable es la no estacionariedad y cambie a GWR con el conjunto completo de variables explicativas que encontró entre todos los modelos de área del subconjunto. Si no encuentra modelos especificado adecuadamente en las áreas de subconjunto más pequeñas, es posible que usted intenta modelar algo que es demasiado complejo para ser reducido a serie sencilla de mediciones numéricas y relaciones lineales. En ese caso, probablemente deba analizar métodos analíticos alternativos.
Esta opción puede suponerle cierto trabajo, pero también es un buen ejercicio en el análisis de datos exploratorios y le ayudará a comprender mejor los datos y buscar nuevas variables para utilizarlas. Incluso puede que sea un buen modelo.
Comprobación 6: ¿Cómo de bien estoy explicando mi variable dependiente?
Ha llegado la hora de evaluar el rendimiento del modelo. El valor R2 ajustado es una medida importante de hasta qué punto sus variables explicativas están modelando su variable dependiente. El valor R2 también es una de las primeras cosas que se aprenden sobre el análisis de regresión. ¿Por qué es importante no activarlo hasta el final? Es posible que no sepa que no puede fiarse de su valor R2, a no ser que haya superado todas las comprobaciones indicadas a continuación. Si el modelo está sesgado, es posible que esté desempeñándose bien en algunas áreas o con un determinado rango de los valores de la variable dependiente, pero que de otro modo no se desempeñan bien en absoluto. El valor R2 no lo refleja. Del mismo modo, si tiene una autocorrelación espacial de los residuales, no puede confiar en las relaciones del coeficiente desde el modelo. Con variables explicativas redundantes, se obtienen valores R2 extremadamente elevados, pero el modelo será inestable; no reflejará las relaciones reales que intenta modelar y puede que produzca resultados completamente diferentes incluso con la inclusión de una sola observación.
Sin embargo, una vez haya revisado el resto de comprobaciones y sienta que satisface todos los criterios necesarios, es el momento de determinar si su modelo explica correctamente los valores para la variable dependiente evaluando el valor R2 ajustado. Los valores de R2 van del 0 al 1 y representan un porcentaje. Suponga que está modelando los índices de criminalidad y encuentra un modelo que supera las cinco comprobaciones anteriores con un valor R2 ajustado de 0,65. Le indica que las variables explicativas del modelo justifican el 65 por ciento de la variación de la variable dependiente del índice de criminalidad. Los valores R2 ajustados se deben evaluar de manera algo subjetiva. En algunas áreas de la ciencia, explicar 23 por ciento de un fenómeno complejo será muy interesante. En otros campos, podría ser necesario que el valor R2 se acerque al 80 o 90 por ciento para merecer mayor atención. Sea como fuere, el valor R2 ajustado le ayudará a juzgar el rendimiento de su modelo.
Otro diagnóstico importante para ayudarlo a evaluar el rendimiento del modelo es el criterio de información de Akaike corregido (AICc). El valor del AICc es una medida útil para comparar varios modelos. Por ejemplo, es posible que quiera probar modelar las puntuaciones de exámenes de los estudiantes usando diversos conjuntos de variables explicativas. En un modelo podría solo usar variables demográficas, mientras que en otro modelo puede seleccionar variables relativas a la escuela y al salón de clase, como el gasto por estudiante y las relaciones profesor-estudiante. Mientras la variable dependiente para todos los modelos que se están comparando es la misma (en este caso, las puntuaciones del examen del estudiante), puede utilizar los valores de AICc de cada modelo para determinar qué funciona mejor. El modelo con el valor del AICc más pequeño proporciona un mejor ajuste a los datos observados.
Y no lo olvide...
Tenga en cuenta que, a medida que realiza los pasos de creación de un modelo de regresión especificado adecuadamente, el objetivo del análisis es, en última instancia, comprender los datos y utilizar ese conocimiento para resolver problemas y responder preguntas. En realidad, podría probar una serie de modelos (con y sin variables transformadas), explorar varias áreas de estudio pequeñas y analizar sus superficies de coeficiente e, incluso así, no encontrar ningún modelo GLR especificado adecuadamente. Pero, y esto es importante, aún estará contribuyendo al cuerpo de conocimientos sobre el fenómeno que se está modelando. Si el modelo del que especuló que sería un indicador preciso resulta que no es significativo en absoluto, su descubrimiento supone información importante. Si una de las variables que creía que sería sólida tiene una relación positiva en algunas áreas y una relación negativa en otras, saber sobre esto, sin duda, aumenta su comprensión del problema. El trabajo que realiza al intentar encontrar un buen modelo con GLR y aplicando después GWR para explorar la variación regional entre las variables del modelo, siempre será valioso.
Para obtener más información sobre el análisis de regresión y tutoriales prácticos, consulte https://www.esriurl.com/spatialstats.