Los datos espaciales a menudo muestran autocorrelación espacial, en la que observaciones cercanas tienen valores similares. Ignorar esto en los modelos de regresión puede conducir a estimaciones sesgadas e inferencias incorrectas.
La herramienta Autorregresión espacial se ha diseñado para afrontar estos desafíos utilizando un modelo de regresión espacial que contabiliza explícitamente la dependencia espacial. La herramienta puede realizar una regresión tradicional ordinaria de mínimos cuadrados o uno de los siguientes modelos de regresión espacial global: el modelo de intervalo espacial, el modelo de error espacial o el modelo combinado autorregresivo espacial. Puede especificar qué modelo utilizará la herramienta o la herramienta puede determinar el modelo más adecuado realizando una serie de pruebas de diagnóstico sobre las variables dependientes y explicativas.
El objetivo de estos modelos de regresión es habilitar una inferencia robusta de modelos de regresión en la presencia de dependencia espacial. Mediante el uso de modelos de regresión espacial, puede tener más confianza en las estimaciones, así como proporcionar estimaciones de los efectos del espacio en sus modelos.
Potenciales aplicaciones
La herramienta de Autorregresión espacial puede utilizarse para explicar la dependencia espacial en los modelos de dos formas principales.
En primer lugar, el modelo de intervalo espacial es valioso para analizar los efectos de desbordamiento espacial, como los siguientes:
- Salud pública y epidemología: determinar la propagación de enfermedades y virus teniendo en cuenta la dependencia espacial.
- Criminología: comprender cómo el crimen se acumula y expande geográficamente, incorporando efectos de vecindarios.
En segundo lugar, el modelo de error espacial puede proporcionar estimaciones de modelo imparciales al tener en cuenta la dependencia espacial en variables explicativas, como las siguientes:
- Análisis socioeconómico: evaluar los logros educativos controlando los efectos correlativos al espacio en variables explanatorias.
- Precios de la vivienda: controlar factores espaciales no controlados que afectan los valores de inmuebles, aportando perspectivas más claras sobre variables claves del modelo.
Tipos de modelo
La herramienta Autorregresión espacial puede determinar tres modelos de regresión espacial globales posibles que contabilicen la dependencia espacial de distintas maneras. La regresión de mínimos cuadrados ordinarios se lleva a cabo cuando ninguno de los tres modelos de regresión espacial se determinan como aptos en función de diversos diagnósticos.
Modelo de error espacial
El modelo de error espacial (SEM) se ha diseñado para abordar situaciones en las que existe autocorrelación espacial en los residuales de un modelo de regresión. Para SEM, la dependencia espacial se considera un parámetro molesto. Un parámetro molesto es aquel que debe tenerse en cuenta para garantizar que se realicen las inferencias adecuadas. El modelo SEM lo define la siguiente fórmula:

Es similar a la fórmula de regresión de mínimos cuadrados ordinarios, en la que una variable dependiente (y) se predice mediante un conjunto de variables explicativas (x) y coeficientes (β). Sin embargo, el plazo residual (u) se modela mediante una ecuación de regresión diferente. Esta segunda regresión predice el residuo utilizando un parámetro autorregresivo espacial λ (lambda) y una matriz de ponderaciones espaciales (W), junto con su propio término residual (ε). El parámetro lambda cuantifica la fuerza de la dependencia espacial en el término de error y mide cuánto influye el término de error de una ubicación en los términos de error de sus vecinos.
El SEM funciona filtrando la autocorrelación espacial de cada una de las variables del modelo y realizando una regresión sobre las variables filtradas espacialmente. Como resultado, las estimaciones de los coeficientes no se ven tan afectadas por la autocorrelación espacial en cada variable.
Modelo de intervalo espacial
A diferencia del SEM, que considera la dependencia espacial como una molestia, el modelo de intervalo espacial (SLM) incorpora la dependencia espacial como una variable explicativa. El modelo de intervalo espacial se utiliza cuando la variable dependiente tiene una gran cantidad de autocorrelación espacial y presenta un efecto de desbordamiento espacial (lo que significa que los cambios en un área provocan cambios en las áreas vecinas). El modelo SLM lo define la ecuación:

La variable dependiente se predice mediante las variables explicativas, así como su propio intervalo espacial (Wy). El parámetro autorregresivo espacial ρ (rho) mide la fuerza de la influencia que los vecinos de una ubicación ejercen sobre el valor de la variable dependiente (y). Los valores estimados más grandes del ρ parámetro sugieren un proceso de difusión en el que los valores en una ubicación afectan a los valores en ubicaciones vecinas. A su vez, los vecinos pueden afectar a la ubicación original, provocando un bucle de retroalimentación.
Modelo combinado autorregresivo espacial
El modelo combinado autorregresivo espacial (SAC) incluye los parámetros autorregresivos espaciales λ y ρ de los modelos de error espacial y de intervalo espacial, respectivamente.
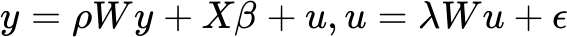
En este caso, se modelan la dependencia espacial del término de error, así como el intervalo espacial de la variable dependiente. El modelo SAC se puede utilizar para identificar los efectos de desbordamiento espacial en la variable dependiente, al tiempo que aborda la dependencia espacial en el término de error.
Elegir el modelo adecuado
De manera predeterminada, la herramienta seleccionará el modelo más apropiado basándose en una serie de pruebas estadísticas denominadas prueba del multiplicador de Lagrange (LM) (también conocida como puntuación de Rao). El proceso de selección se basa principalmente en el flujo de trabajo descrito por Anselin y Rey (2014).
Los criterios de decisión para seleccionar el modelo se muestran en el siguiente diagrama de flujo:
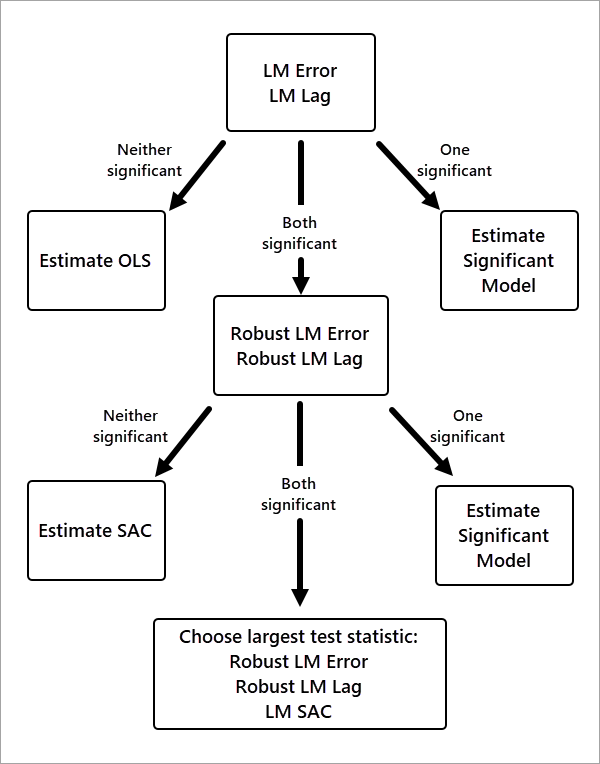
En primer lugar, se realiza la prueba LM para los modelos de intervalo espacial (Intervalo LM) y de error espacial (Error LM). Si ninguna de las pruebas es estadísticamente significativa (valor p superior a 0,05), no es necesario un modelo espacial y se selecciona un modelo OLS. Si solo una de las pruebas es significativa, se selecciona el modelo correspondiente.
Si las pruebas de intervalo LM y de error LM son significativas, se realizan sus equivalentes robustos. Estas son las pruebas Intervalo LM robusto y Error LM robusto, que son formas ligeramente más estrictas de la prueba. Si solo una de las pruebas es significativa, se selecciona el modelo correspondiente.
Si ambas pruebas pruebas son significativas, se realiza una prueba LM para el modelo SAC. En caso de que las tres pruebas sean significativas, se elige el modelo con la mayor estadística de prueba.
En el raro caso de que tanto la prueba de intervalo LM como la de error LM sean significativas, pero ninguna de las pruebas robustas lo sea, se elige el modelo SAC.
Es importante señalar que las pruebas LM son un planteamiento basado en datos para elegir un modelo. No garantizan un modelo o ajuste buenos. Consulte los diagnósticos y considere los supuestos teóricos del modelo.
Salidas de la herramienta
El resultado principal de la herramienta es una serie de tablas en los mensajes de geoprocesamiento, así como una clase de entidad de salida y un gráfico que visualiza los valores residuales del modelo.
Entidades de salida
La clase de entidad de salida de la herramienta contendrá campos de la variable dependiente, variables explicativas, el valor predicho de la variable dependiente, el residual y el residual estandarizado, el intervalo espacial del residual y el número de vecinos de cada entidad.
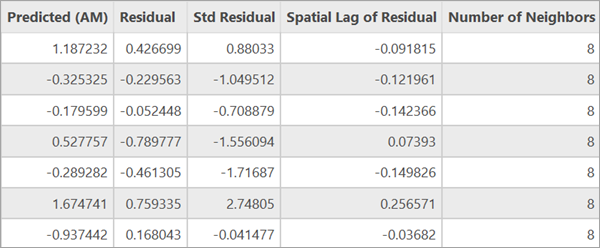
Cuando se agrega la capa a un mapa, las entidades se sombrearán según sus valores residuales estandarizados. La visualización de los residuos estandarizados puede ayudar a identificar cualquier patrón de clústeres en el término de error.

Los valores residuales se simbolizan desde un morado intenso hasta un verde oscuro. Las ubicaciones simbolizadas en verde tienen un valor residual positivo, lo que significa que el modelo sobrevaloró el valor. Del mismo modo, las ubicaciones con un color morado tienen un residual estandarizado negativo. Los valores residuales negativos indican una ubicación que está subestimada.
Gráfico de dispersión de Moran de residuales
La capa de salida contiene un gráfico de dispersión que muestra los valores residuales trazados frente a su intervalo espacial. El eje x muestra el residual estandarizado y el eje y muestra el intervalo espacial del residual estandarizado. Este tipo de gráfico se conoce como diagrama de dispersión de Moran.
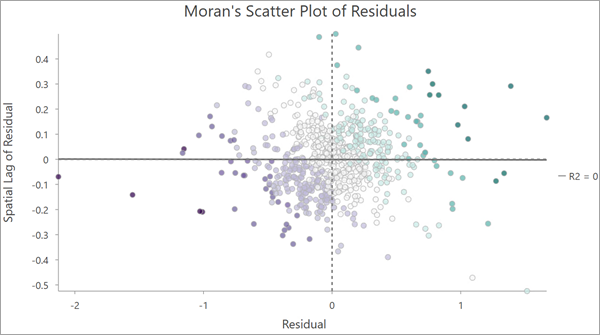
El gráfico puede dividirse en cuatro cuadrantes alrededor de 0 en los ejes x e y. Los valores en los cuadrantes superior derecho e inferior izquierdo muestran una autocorrelación espacial positiva. Estas son ubicaciones que tienen valores similares a los de sus vecinos: valores positivos y negativos, respectivamente. Los cuadrantes superior izquierdo e inferior derecho son ubicaciones que presentan autocorrelación espacial negativa. Estas son ubicaciones que tienen valores altos rodeados de valores bajos (y viceversa).
Cuando los valores residuales se distribuyen uniformemente en los cuatro cuadrantes, indica que no hay autocorrelación espacial discernible. Este tipo de patrón es de esperar cuando el modelo de regresión ha funcionado bien y se ha tenido en cuenta la mayor parte de la autocorrelación espacial.
Mensajes de geoprocesamiento
La herramienta proporciona una serie de tablas en los mensajes de geoprocesamiento que ofrecen una perspectiva de cómo se estima cada modelo:
- Resumen de ponderaciones espaciales y de vecindad
- Resultados de la prueba LM
- Resumen de resultados de modelo
- Diagnóstico de modelo
En algunos casos, las tablas también muestran el siguiente mensaje:
- Resumen de los efectos de los coeficientes
- Informe de puntos coincidentes
Cada tabla se describe en las siguientes secciones.
Resumen de ponderaciones espaciales y de vecindad
Los modelos SEM, SLM y SAC requieren una matriz de ponderaciones espaciales, que puede influir en gran medida en los resultados del modelo. La tabla de Resumen de ponderaciones espaciales y de vecindad proporciona una perspectiva sobre la matriz de ponderaciones espaciales utilizada para ajustar el modelo. Informa sobre el tipo de vecindario, el esquema de ponderación, la conectividad espacial, el tamaño medio del vecindario, el tamaño mínimo del vecindario y el tamaño máximo del vecindario.

Es importante tener en cuenta que la herramienta no estimará un modelo si la matriz de ponderaciones espaciales está demasiado conectada. El porcentaje de conectividad espacial es aproximadamente el número medio de vecinos para cada entidad, como porcentaje del número total de entidades. Por ejemplo, con 500 entidades y una conectividad espacial igual a 0,1, cada entidad tendrá aproximadamente 50 vecinos de media. Si la matriz de ponderaciones espaciales tiene una conectividad del 30 por ciento o más, los resultados del modelo estarán sesgados (Smith, 2009). En este caso, la herramienta devolverá un error.
Resultados de la prueba LM
La tabla de resultados de la prueba LM muestra los diagnósticos del multiplicador de Lagrange para cada una de las pruebas. La tabla también muestra el tipo de modelo que se seleccionaría según el gráfico de flujo de la sección anterior, Elegir el modelo adecuado.

Informe de puntos coincidentes
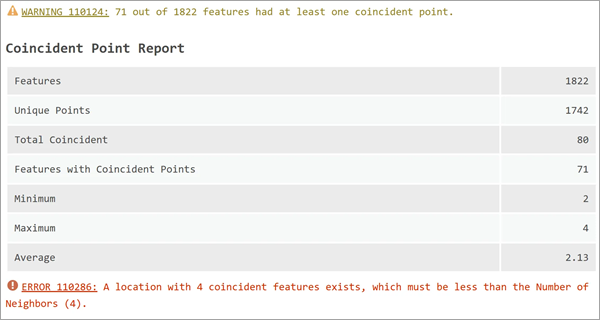
Los puntos coincidentes (puntos con las mismas coordenadas) pueden causar varios problemas en la regresión espacial, como la creación de pesos iguales a cero para todos los vecinos. Si hay puntos coincidentes en sus entidades de entrada, se mostrará un Informe de puntos coincidentes que informa del total de entidades, el número de ubicaciones únicas, así como el número mínimo, máximo y medio de puntos coincidentes para todas las entidades. Además, pueden mostrarse advertencias y errores causados por los puntos coincidentes.
Diagnóstico de modelo
La tabla de Diagnósticos del modelo muestra diagnósticos importantes, como la variable dependiente, el número de entidades, los grados de libertad, así como el modelo utilizado.
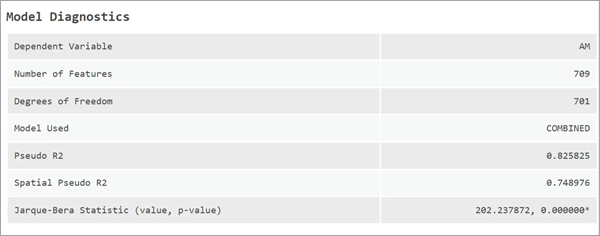
Si se estima un modelo OLS, el R cuadrado ajustado se muestra en la tabla. Sin embargo, para todos los modelos espaciales, se muestra en su lugar un pseudo R cuadrado. Para los modelos SLM y SAC, también se muestra un pseudo R cuadrado espacial. Esto se aborda más adelante.
Además, también se informa de la estadística de Jarque-Bera. Si la estadística es significativa, indica que los valores residuales del modelo no tienen una distribución normal. Aunque los modelos se estiman utilizando métodos robustos a la no normalidad, la prueba puede indicar una especificación errónea del modelo o la presencia de valores atípicos.
Interpretar los resultados del modelo de intervalo espacial
El modelo de intervalo espacial informa de un coeficiente adicional llamado Intervalo Y (rho). Este es el intervalo espacial de la variable dependiente. El coeficiente de esta variable mide la fuerza y la dirección de la dependencia espacial de la variable dependiente. El valor de rho debe estar comprendido entre -1 y 1. Los valores más altos del Intervalo Y sugieren un fuerte proceso de retroalimentación espacial.

Es importante tener en cuenta que un cambio en una variable explicativa en una ubicación puede afectar al valor de la variable dependiente en otra ubicación, lo que se denomina efecto de propagación espacial. En presencia de un efecto de desbordamiento espacial, los coeficientes de regresión deben interpretarse junto con el efecto de desbordamiento espacial.
Impactos y efectos de los coeficientes
Además de los coeficientes de regresión, se informa de una medida denominada impactos. Los impactos ayudan a medir el efecto de los desbordamientos espaciales para cada variable explicativa. Se desglosan en impactos directos, indirectos y totales. Existen otros planteamientos para calcular los impactos, y esta herramienta informa de impactos simples. Los impactos directos, indirectos y totales se muestran en la tabla de mensajes Resumen de efectos del coeficiente.

El impacto directo mide cuánto afecta un cambio de una unidad en una variable explicativa al valor de la variable dependiente en la propia ubicación. En el caso de impactos simples, este es el mismo valor que el coeficiente beta.
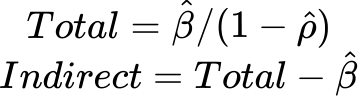
Mientras que el impacto indirecto mide cuánto afecta un cambio de una unidad en una variable a la variable dependiente en sus ubicaciones vecinas. Sin embargo, tenga en cuenta que el valor de los impactos está fuertemente influenciado por la matriz de ponderaciones espaciales.
Errores estándar
De forma predeterminada, el modelo de intervalo espacial informa de errores estandarizados robustos. Sin embargo, después de ajustar un modelo de intervalo espacial, puede quedar una gran cantidad de autocorrelación en los valores residuales. La prueba de Anselin-Kelejian (AK) es una prueba de diagnóstico que se utiliza para determinar si queda una cantidad significativa de dependencia espacial en los valores residuales del modelo.

Si la prueba AK es significativa (valor p inferior a 0,05), se informa de otra medida del error estándar, denominada errores estándar heterocedásticos y autocorrelacionados (HAC). Los errores estándar HAC son una variante no paramétrica de los errores estándar que resultan útiles en presencia de autocorrelación espacial.

Los errores estandarizados de HAC tienen en cuenta la distribución espacial de los datos mediante el uso de una matriz de ponderaciones espaciales independiente. La matriz de ponderaciones espaciales se crea utilizando los k vecinos más cercanos para identificar el vecindario de cada entidad con la entidad focal incluida en el vecindario. Los pesos de cada vecindario se modelan utilizando un kernel triangular.
Pseudo R cuadrado y pseudo R cuadrado espacial
Dado que el modelo de intervalo espacial incluye el intervalo espacial de la variable dependiente como variable explicativa, no se pueden utilizar los métodos tradicionales de predicción por regresión lineal. Predecir la variable dependiente utilizando su intervalo espacial conduce a estimaciones demasiado confiadas. Para solucionar esto, se calcula otra medida llamada pseudo R cuadrado espacial.
Este pseudo R cuadrado espacial se calcula sin el intervalo espacial de la variable dependiente. En su lugar, utiliza la matriz de ponderaciones espaciales y la estimación de λ para crear unos valores previstos de Wy-hat que se utilizan en lugar de Wy en la predicción.
Los valores de predicción se utilizan entonces para calcular un valor tradicional de pseudo R cuadrado. Se recomienda que informe del valor espacial del pseudo R cuadrado sobre el valor del pseudo R cuadrado.
Es importante señalar que el pseudo R cuadrado espacial es otra medición diferente al R cuadrado ajustado que se informa en los resultados de OLS. Por lo tanto, no es apropiado compararlos.
Interpretar los resultados del modelo de error espacial
En el modelo de error espacial, los coeficientes de regresión pueden interpretarse de manera similar a los de la regresión lineal estándar. Cada coeficiente representa el cambio en la variable dependiente para un cambio de una unidad en la variable independiente. Sin embargo, el SEM también incluye un componente adicional, el valor residual de intervalo (lambda), que desempeña un rol crucial en la comprensión de la dependencia espacial dentro del modelo. El coeficiente del valor residual de intervalo (lambda) estará siempre entre -0,99 y 0,99.

Un valor positivo de lambda sugiere que los valores residuales muestran un clustering espacial y un valor negativo de lambda indica que los valores residuales muestran una dispersión espacial. Los valores absolutos más grandes (positivos o negativos) de lambda también sugieren que hay procesos espaciales que no son tenidos en cuenta por las variables explicativas. La inclusión de variables explicativas adicionales pertinentes puede reducir el coeficiente a niveles más moderados.
Interpretar los resultados del modelo combinado autorregresivo espacial
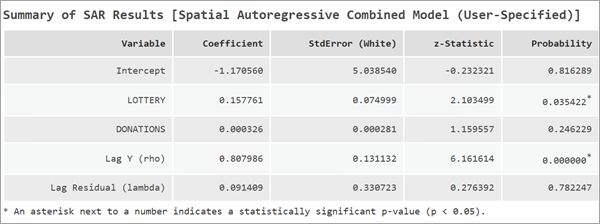
Cuando se selecciona el modelo SAC, todas las secciones aplicables a los modelos SLM y SEM se muestran en los mensajes.
Referencias
Para implementar la herramienta, se utilizaron los siguientes recursos:
- Anselin, L., and Sergio J. Rey. 2014. "Modern spatial econometrics in practice: A guide to GeoDa, GeoDaSpace and PySAL." ISBN 9780986342103.
Bivand, Roger and Gianfranco Piras. 2015. "Comparing implementations of estimation methods for spatial econometrics." Journal of Statistical Software. 63: 1-36. https://doi.org/10.18637/jss.v063.i18.
Kelejian, Harry H., and Ingmar R. Prucha. 2007. "HAC estimation in a spatial framework." Journal of Econometrics. 140, no. 1: 131-154. https://doi.org/10.1016/j.jeconom.2006.09.005.
Smith, Tony E. 2009. "Estimation bias in spatial models with strongly connected weight matrices." Geographical Analysis. 41, no. 3: 307-332. https://doi.org/10.1111/j.1538-4632.2009.00758.x.