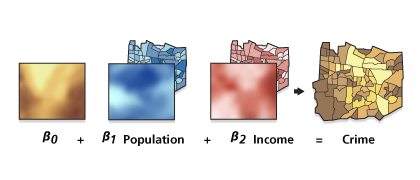
Esta herramienta realiza una Regresión ponderada geográficamente, una forma local de regresión que se utiliza para modelar las relaciones que varían espacialmente. La herramienta GWR ofrece un modelo local de la variable o el proceso que trata de comprender o predecir ajustando una ecuación de regresión a todas las entidades del dataset. La herramienta (GWR) crea dichas ecuaciones separadas incorporando las variables dependientes y explicativas de entidades que se encuentran dentro de la vecindad de cada entidad de destino. La forma y extensión de todas las vecindades que se analizan se basan en la entrada de los parámetros Tipo de vecindad y Método de selección de vecindad con una restricción: si el número de entidades vecinas es superior a 1000, solo las 1000 más cercanas se incorporan a cada una de las ecuaciones locales.
Utilice esta herramienta en datasets con varios cientos de entidades. No es una herramienta adecuada para datasets pequeños. La herramienta no funciona con datos de multipunto.
Use el parámetro Entidades de entrada con un campo que represente el fenómeno que está modelando (el valor Variable dependiente) y uno o varios campos que representen el valor Variables explicativas. Estos campos deben ser numéricos y tener un rango de valores. Las entidades que contienen valores que faltan en la variable explicativa o dependiente se excluirán del análisis; sin embargo, es posible usar la herramienta Rellenar valores que faltan para completar el dataset antes de ejecutar la herramienta GWR.
La herramienta GWR produce una variedad de salidas. Dispone de un resumen del modelo Regresión ponderada geográficamente como un mensaje en la parte inferior del panel Geoprocesamiento durante el funcionamiento de la herramienta. Para acceder al mensaje, pase el cursor sobre la barra de progreso y haga clic en el botón emergente o expanda la sección de mensajes del panel Geoprocesamiento. También puede acceder a los mensajes de una herramienta GWR ejecutada anteriormente a través del historial de geoprocesamiento.
La herramienta acepta puntos y polígonos como entrada. En el caso de los polígonos, todas las distancias y los vecinos se determinan mediante el uso de la distancia entre los centroides de los polígonos (puntos). Sin embargo, un solo punto podría no ser una buena representación del polígono, sobre todo en el caso de polígonos grandes, alargados o multiparte. En estos casos, los vecinos y las distancias entre polígonos podrían ser poco intuitivos o erróneos. Por ejemplo, dos polígonos que comparten un borde podrían no considerarse vecinos si sus centroides están separados. Para ver los centroides utilizados por esta herramienta, utilice la herramienta De entidad a punto con el parámetro Dentro desactivado para convertir los polígonos en puntos de centroide. También puede utilizar Explorador de vecindad para visualizar los vecinos de los puntos de centroide o polígonos.
En general, no se recomienda efectuar la regresión ponderada geográficamente en las líneas porque el centroide no suele ser una representación adecuada de la línea. Sin embargo, para utilizar líneas en la herramienta puede utilizar la herramienta De entidad a punto para convertir las líneas en puntos de centroide y usar los centroides en la herramienta. Los resultados se pueden unir de nuevo a las líneas originales.
El valor del parámetro Tipo de modelo especificado depende de los datos que esté modelando. Es importante usar el modelo correcto para el análisis con el fin de obtener resultados precisos del análisis de regresión.
Es recomendable usar datos proyectados. Es especialmente importante cuando la distancia es un componente del análisis, como lo es para Regresión ponderada geográficamente cuando especifica Banda de distancia para el parámetro Tipo de vecindad. Se recomienda que los datos estén proyectados mediante un sistema de coordenadas proyectadas (en lugar de un sistema de coordenadas geográficas).
Algunos de los cómputos pueden utilizar varias CPU para incrementar el rendimiento y utilizarán automáticamente hasta ocho subprocesos/CPU para el procesamiento.
Es una práctica habitual explorar los datos globalmente con la herramienta Regresión lineal generalizada antes de explorar los datos localmente con esta herramienta.
Los valores de los parámetros Variable dependiente y Variables explicativas deben ser campos numéricos con una serie de valores. Estos valores deben variar tanto globalmente como localmente. Por este motivo, no utilice variables explicativas falsas para representar regímenes espaciales diferentes en el modelo Regresión ponderada geográficamente (como asignar un valor de 1 a los distritos censales que están fuera del núcleo urbano, mientras que al resto se les asigna un valor de 0). Ya que la herramienta GWR permite que los coeficientes de la variable explicativa varíen, estas variables explicativas del régimen espacial no son necesarias, y si se incluyen, crearán problemas con la multicolinealidad local.
En los modelos de regresión global, como la Regresión lineal generalizada, los resultados son poco fiables cuando dos o más variables exhiben multicolinealidad (cuando dos o más variables son redundantes o cuentan la misma historia). La herramienta GWR construye una ecuación de regresión local para cada entidad del dataset. Cuando los valores para una variable explicativa particular se agrupan espacialmente en clústeres, es muy probable que tenga problemas con la multicolinealidad local. El campo del número de condición (COND) de la clase de entidad de salida indica el momento en el que los resultados son inestables debido a la multicolinealidad local. En general, sospeche de resultados para entidades con un número de condición mayor que 30, igual que Nulo o, para los shapefiles, igual a -1,7976931348623158e+308. Este número de condición está ajustado a escala para corregirse para el número de variables explicativas en el modelo. Esto permite una comparación directa del número de condición entre modelos usando diferentes números de variables explicativas.
Tenga cuidado al incluir datos nominales o de categorías en un modelo Regresión ponderada geográficamente. Donde las categorías se agrupan espacialmente, existe el riesgo de encontrar problemas de multicolinealidad local. El número de condición incluido en la salida de Regresión ponderada geográficamente indica cuándo la colinealidad local es un problema (un número de condición menor que 0, mayor que 30 o establecido en Nulo). Cuando existe una multicolinealidad local, los resultados son inestables.
Para comprender mejor la variación regional entre los coeficientes de las variables explicativas, examine las superficies de coeficiente ráster opcionales creadas por la herramienta GWR. Estas superficies de ráster se crean en el parámetro Espacio de trabajo coeficiente ráster bajo Opciones adicionales, si se especifica. Para los datos de polígono, puede utilizar un color graduado o una representación en pantalla de frío a cálido en cada campo de coeficiente en el valor de Entidades de salida para examinar los cambios en el área de estudio.
Puede usar la herramienta GWR para hacer una predicción suministrando un valor para Ubicaciones de predicción (a menudo, esta clase de entidad es la misma que el valor de Entidades de entrada), haciendo coincidir las variables explicativas y especificando un valor para Entidades predichas de salida. Si los campos Variables explicativas para combinar del valor de Entidades de entrada coinciden con los campos Campos de ubicaciones de predicción, se rellenarán automáticamente. De lo contrario, especifique los campos adecuados.
Un modelo de regresión está mal especificado si falta una variable explicativa clave. Si la autocorrelación espacial de los residuales de regresión o la variación espacial no esperada entre los coeficientes de una o más variables explicativas son estadísticamente significativas, se puede intuir que el modelo está mal especificado. Haga todo lo posible (por ejemplo, a través del análisis de residual de Regresión lineal generalizada y el análisis de variación del coeficiente de Regresión ponderada geográficamente) para descubrir estas variables clave que faltan y poder incluirlas en el modelo.
Determine si tiene sentido que una variable explicativa sea no estacionaria. Por ejemplo, supongamos que está modelando la densidad de una especie de planta en particular como función de muchas variables incluida la de la ORIENTACIÓN. Si descubre que el coeficiente de la variable ORIENTACIÓN cambia en el área de estudio, es probable que sea la prueba de que falta una variable explicativa clave (la prevalencia de una vegetación rival, por ejemplo). Haga todo lo posible para incluir todas las variables explicativas clave en el modelo de regresión.
Cuando el resultado de un cómputo es infinito o indefinido, el resultado para los no shapefiles será Nulo; para los shapefiles, el resultado será -DBL_MAX = -1,7976931348623158e+308.
Precaución:
Sin embargo, los shapefiles no pueden almacenar valores nulos. Por consiguiente, las herramientas u otros procedimientos que crean shapefiles a partir de entradas que no son shapefiles pueden almacenar valores nulos como cero o un número negativo muy pequeño (-DBL_MAX = -1,7976931348623158e+308). Esto puede ocasionar resultados inesperados. Para más información, consulte Cuestiones de geoprocesamiento para el shapefile de salida.
Dispone de tres opciones para el parámetro Método de selección de vecindad. Si especifica Búsqueda dorada, la herramienta encontrará los mejores valores de los parámetros Banda de distancia o Cantidad de vecinos si está utilizando el método búsqueda por sección dorada. La opción Intervalos manuales evaluará los vecindarios en incrementos entre las distancias especificadas. En cualquier caso, el tamaño de vecindad que se utiliza es aquel que minimiza el valor del criterio de información de Akaike (AICc). Sin embargo, los problemas con la multicolinealidad local evitarán que estos métodos resuelvan una banda de distancia o cantidad de vecinos óptimas. Si aparece un error o se producen problemas graves en el diseño del modelo, intente especificar una distancia o recuento de vecindad en particular con la opción Definido por el usuario. Después, examine los números de condiciones en la clase de entidad de salida para determinar qué entidades están asociadas con los problemas de colinealidad local.
Los problemas graves de diseño del modelo o los errores que indican que las ecuaciones locales no incluyen suficientes vecinos por lo general señalan que existe un problema con la multicolinealidad global o local. Para determinar dónde está el problema, ejecute un modelo global con la herramienta Regresión lineal generalizada y examine el valor VIF para cada variable explicativa. Si algunos de los valores VIF son grandes (por ejemplo, mayores que 7,5), la multicolinealidad global impide que Regresión ponderada geográficamente se resuelva. Sin embargo, es más probable que la multicolinealidad local sea el problema. Intente crear un mapa temático para cada variable explicativa. Si el mapa muestra un clustering espacial de valores idénticos, considere quitar esas variables del modelo o combinarlas con otras variables explicativas para aumentar la variación del valor. Por ejemplo, si está modelando valores de viviendas y tiene variables tanto para los dormitorios como para cuartos de baño, puede combinarlas para aumentar la variación del valor o para representarlas como metros cuadrados de cuarto de baño/dormitorio. Evite utilizar variables falsas del régimen espacial, clustering espacial de variables categóricas o nominales o variables con pocos valores posibles al construir modelos Regresión ponderada geográficamente.
Regresión ponderada geográficamente es un modelo lineal sujeto a los mismos requisitos que Regresión lineal generalizada. Consulte los diagnósticos explicados en Cómo funciona Regresión ponderada geográficamente para asegurarse de que su modelo Regresión ponderada geográficamente esté especificado correctamente. La sección Cómo dejan de funcionar los modelos de regresión del tema Conceptos básicos del análisis de regresión también incluye información para asegurarse de que el modelo sea preciso.